前回は「整数問題の解き方・考え方〜まずは倍数を考える・大きな数字を考える・最小公倍数・文章から具体的にイメージ〜」の話でした。
「入れ替える」ことを具体的にイメージ：物々交換とコイン
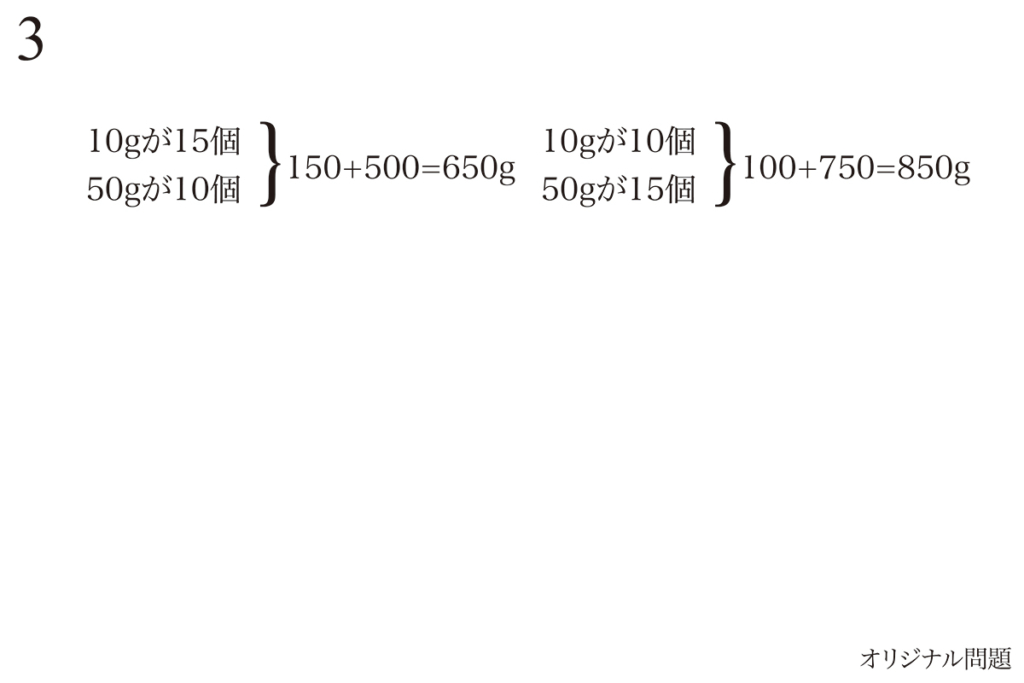
今回は、整数問題必勝法「具体例で実験して理解、問題を解けるようになる」話です。
問題３の解き方で、「実験して考える」話をご紹介しました。（上記リンク）
問題９も共通しますが、「入れ替える」問題はよくあります。
コインを入れ替えたり、食塩水を入れ替えたり、いろいろなモノを入れ替えることがあります。
「AとBの食塩水を同じ量入れ替えて・・・」という問題も、比較的見かけます。
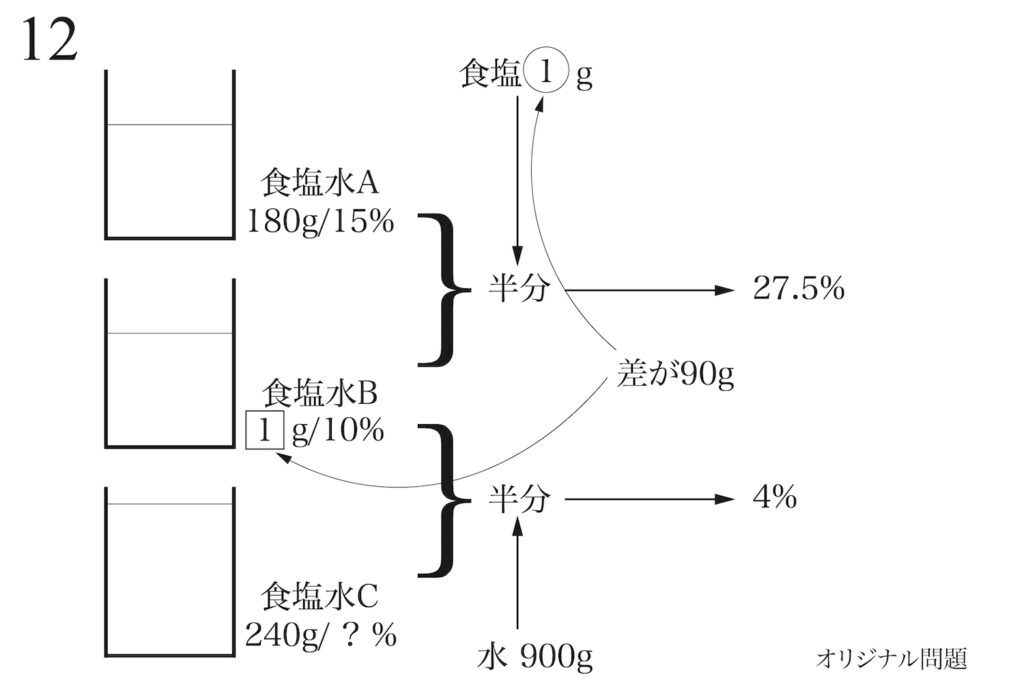
いくつかの食塩水を「半分にする、一部を混ぜる」のも、「入れ替える」問題の応用とも考えられます。
「入れ替える」は、友達と「交換する」ことをイメージしましょう。
ポケモンカードなどをお友達と、
男子小学生僕は、このカード
あげるよ・・・
友達Aくんじゃ、僕は、
このカードあげるから、交換ね！
双方で「欲しいカード同士を交換」することもあるでしょう。
1990年に中学受験をした僕の世代は、小学生の時「カード」は、あまり見かけませんでした。
筆者の世代の方は、小学校低学年で大変な勢いで流行った「キンケシ」をたくさん持っていて、
小学生の筆者昨日のガチャの、このロビンマスク
持っていたんだけど・・・
友達Bくん僕、そのロビン、欲しい！
このラーメンマンと交換しない？
小学生の筆者ああ、
いいよ！
「お互い欲しいキンケシが増える」ことになり「お互いが嬉しいこと」になります。
このことは、「昔、お金・通貨がなかった時代」の物々交換と同じ考え方です。
「お金・通貨がなかった時代」は、食べ物などを物々交換していました。
昔の人Sさんこのお魚
あげるから、お米と交換しよう！
昔の人Tさんこの魚は、私たち家族の好物だから、
これくらいのお米でいかがですか？
昔の人Sさんありがとう！
じゃ、交換だ！
このように「お魚とお米で物々交換」したり、
昔の人Uさんこの珍しい宝石差し上げるから、
お米と交換してください。
昔の人Tさんこの魚は、私たち家族の好物だから、
これくらいのお米でいかがですか？
昔の人Uさんいや、もっと珍しい貴重な宝石だから、
その倍くらいは頂かないと・・・
このように「モノの量の交渉」もあったでしょう。
「モノの値段」が明快な物々交換もあるかもしれませんが、多くは「その場で交渉」です。
すると、
昔の人Uさん分かりにくいし、
交渉が大変・・・
昔の人Tさんもっと客観的な数値があって、
別の「交換する基準となるモノ」があるといいな・・・
こういう思いから生まれたのが「お金・通貨」です。
「お金・通貨」は、国家・社会にとって極めて大事な存在で、根幹を成します。
版籍奉還・廃藩置県のプロセスで、当時存在していた「藩札」。（上記リンク）
幕府の金貨・銀貨・藩札の統一もまた、新政府の大きな課題でした。
具体例で実験して状況を理解
分かりやすいようで、なかなかわからないことが多い「入れ替える」こと。
「入れ替える」自体は分かりやすいですが、
男子小学生入れ替えたら
どうなるか？
「どうなるか」を考えると、
男子小学生あれ？
どうなるのかな？
「分かるはず」なのに「分からなくなる」ことがあります。
「よくわからない時」は実験してみましょう。
「実験してみる」は整数問題に限らず、様々な問題で応用できます。
場合の数の問題などで、「見たことのない問題」が出ることがあります。
出題者が「特殊な条件」を設定して、工夫していることがあります。
「出題文の内容は分かるけど、具体的にはよく分からない」時。
そういう時は、簡単な例を自分で考えて実験してみましょう。
例えば、
出題者5人の人がいて、
〜の条件のもとに、カードを交換します・・・
このような問題が出たとします。
５人は結構多いです。
そこで、５人いる絵を書いて考えてみても、なかなかイメージが湧かないことがあります。
その場合、
女子小学生もし２人だったら、
どうなるのかな・・・
あるいは、
男子小学生もし
３人だったら・・・
少し人数を減らしてみると、分かりやすくなることがあります。
少し対象を少なく、小さくして実験してみると、
男子小学生ああ、
そういうことか！
何かに気づけば、問題を解く鍵が見つかったことになります。
「実験する」ことは、時間が少しかかります。
それでも、「悩んで時間が過ぎてしまう」よりも「解ける可能性が高くなる」ので良いでしょう。
たいていは、こういう実験は「試験用紙の余白に書く」ことが多いです。
記述式の場合、こういう「実験」は遠慮せずに答案の最初の方に書いても良いでしょう。
男子小学生ここは
関係ないんだけど・・・
「関係ないですよ」と説明したかったら、カギ括弧でくくりましょう。
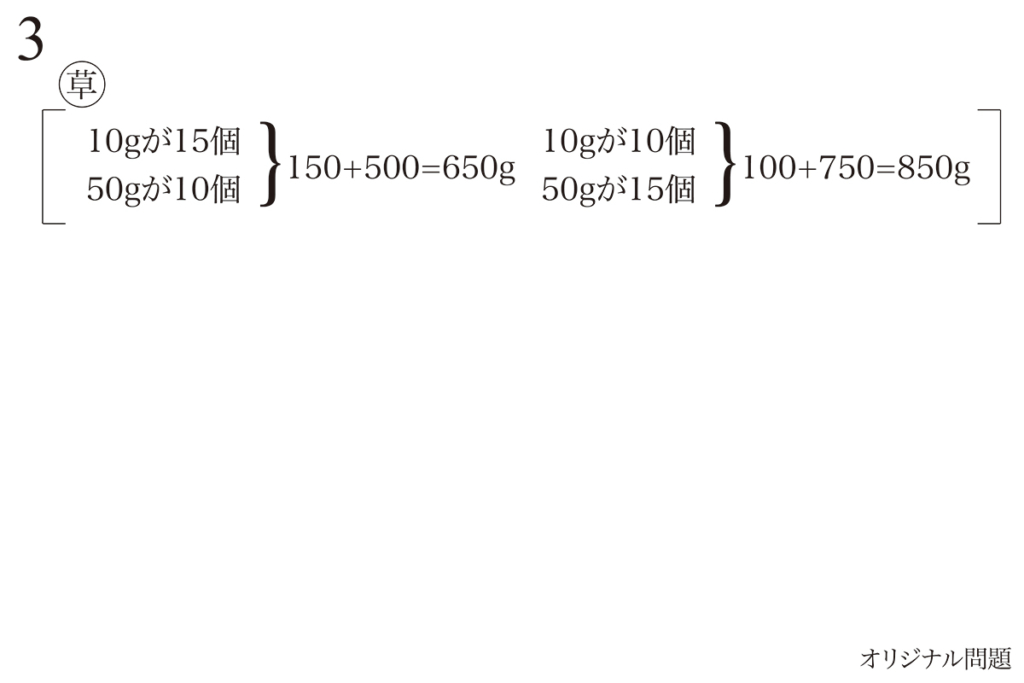
括弧で括って、「草案ですよ」というマークを書いておけば、
採点者ああ、ここは
具体例で考えていたんだな・・・
採点者は一目で分かるでしょう。
そして、記述問題の場合は、答えまで到達していない場合でも、
採点者何か取り組んでいるのは、
評価できる・・・
採点者は「何か考えていること」にきちんと気づいて、
採点者ちょっと点数を
あげよう・・・
「解けていなくても、何らかの点数になる」こともあるでしょう。
奇数と偶数：対象を半分にする
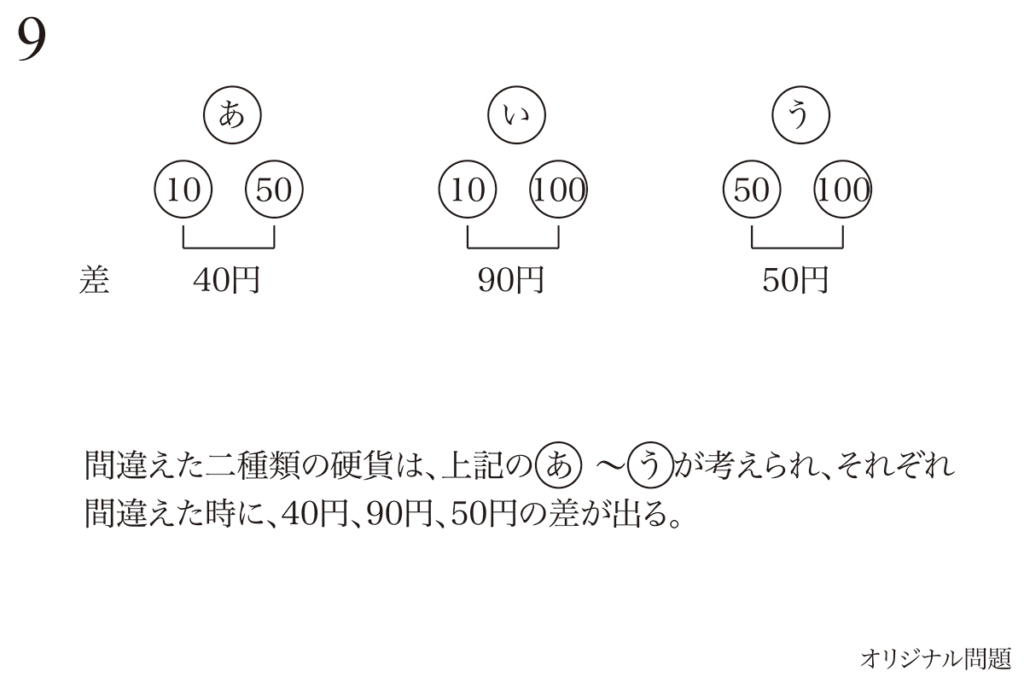
問題９では「取り替えなかった硬貨は奇数」という条件がありました。
奇数・偶数は非常に分かりやすく、どちらかならば「対象は半分」になります。（上記リンク）
整数問題の、「〜の倍数」や「奇数・偶数」は「対象を絞る」ことにつながります。
対象が6の倍数ならば、「対象が1/6に絞れる」ことになります。
それに対して、「奇数・偶数」は「1/2にしか絞れない」ので早い時点では、決定打になりにくいです。
この解答では、最後の方で「奇数・偶数」が出ました。
「奇数・偶数」で問題に出てきたら、
男子小学生どのタイミングで
使う条件かな・・・
こう考えて、○で囲っておきましょう。
問題９のように、「偶数-偶数=偶数」「奇数-偶数=奇数」などは一言書いた方が良いです。
記述式で時間が惜しい時は、「ぐーぐ＝ぐ」「きーぐ＝き」などと略しても良いでしょう。
採点者ちゃんと
分かっているね！
メモでも「分かっている」ことを表現すると、点数がアップする可能性があります。
簡略化した書き方=採点者へのメッセージ
そういう「簡略化した書き方」でも、採点者は分かります。
「ちょっとした事」で、
男子小学生書いた方が
いいだろうけど・・・
男子小学生書く時間が
もったいない・・・
このような時は、略して書いてみましょう。
頭で考えるだけよりも、書くことで自分で確認できます。
そして、意外と「頭だけで考えるとミスする」ことが多いですが、ミスを防ぐことにもなります。
「きーぐ＝き（奇数-偶数=奇数）」なのに、
男子小学生あっ、「きーぐ＝ぐ」と
勘違いしそうになったけど・・・
男子小学生ちょっとメモした方が、
間違えない！
途中で時間切れになっても、「分かっているところ」まで書くこと。
それは、採点者に対する明確なメッセージになります。
女子小学生全部は、
出来なかったけど・・・
女子小学生ここまでは、
ちゃんと分かっています！
遠慮せずに、「略しても、考えていることはきちんと表現」しましょう。
採点者答えには辿り着いて
いないけど・・・
採点者ここまでは、
出来ているんだな・・・
採点者まあ・・・０点ではなく
３点だな・・・
記述式や「式や考え方を書く」時、少しでも点数が入る可能性が高くなるでしょう。
そういう姿勢が、少しでも合格へ近づくことにつながるでしょう。
次回は下記リンクです。
