合格の秘訣・丁寧にポイントを探す〜「解く鍵」をテンポ良く発見する考え方・対称な図形の中心は「へそ」・異なる視点で見て考える〜｜中学受験・算数

前回は「「伸びない・解けない」から「伸びる・出来る」勉強法〜条件を明確化・いくつか補助線を引いてみる姿勢・将来につながる「なぜ？」「どうして？」・試験対策と本質的学力〜」の話でした。

合格の秘訣・丁寧にポイントを探す

今回は、中学受験の算数の本番の入試での取り組み方の話です。

算数は、理科・社会・国語と大きく異なる面があります。

それは、他の科目よりも算数は「急いで考える」傾向が強いです。

理科でも社会でも、問題を解く際には、

試験時間という限られた時間の中で問題を解くので、どうしても気持ちがはやります。

それでも、例えば社会の問題を解く場合は、「解く早さ」にはそれほど大差は出ないです。

問題文を読むのが早かったり、瞬発力が高い方もいるでしょうが、早さより正確さの方が大事です。

対して、算数は、

「解くポイント」が分かれば、比較的サラッと出来るかもしれませんが、

手が止まってしまうと、「時間ばかりが経過してしまう」傾向が強い算数。

そのため、

他の科目よりも、気ばかりがはやってしまう傾向があるのが算数です。

他の科目と同様に、算数も「丁寧にポイントを探す」ことが大事です。

理科や社会の選択肢の問題なら、

このように、とにかく「考えることができる」傾向があります。

ところが、算数の問題は「選択肢」であることは、かなり少ないです。

そのため、他の科目比較すると、ある意味「なんとでも考えることが出来る」のが算数です。

特に難問の大問では、「なんとでも出来る」ように感じられてしまい、

「解答にたどり着く」ことを急いでしまいますが、「じっくりとテンポ良く考える」ことが大事です。

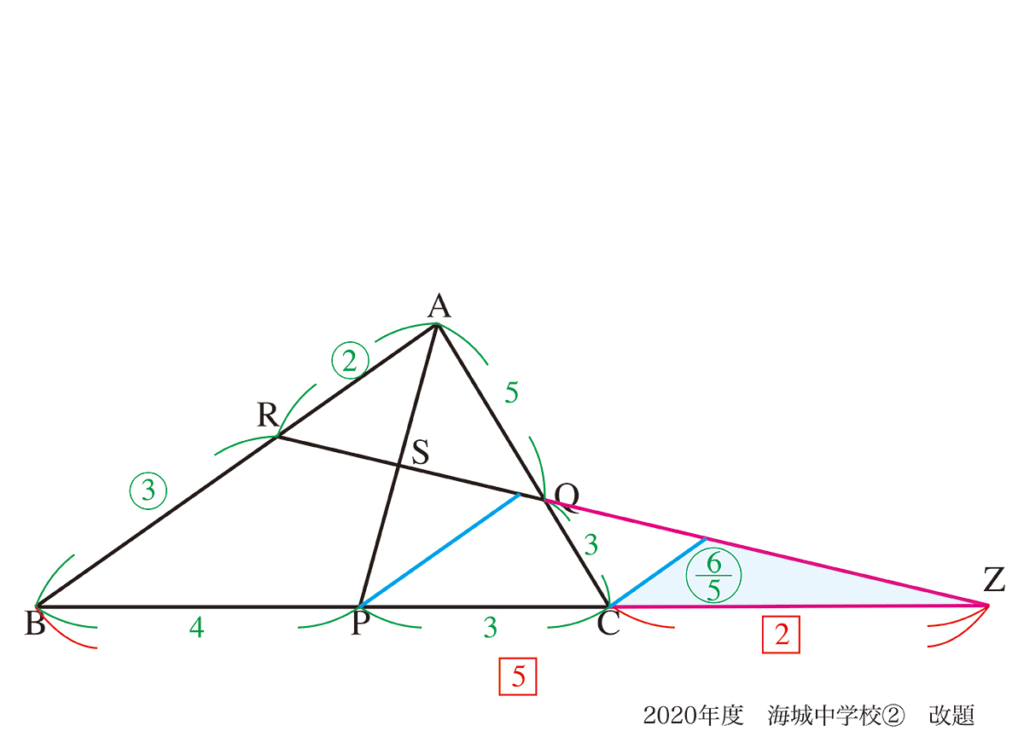
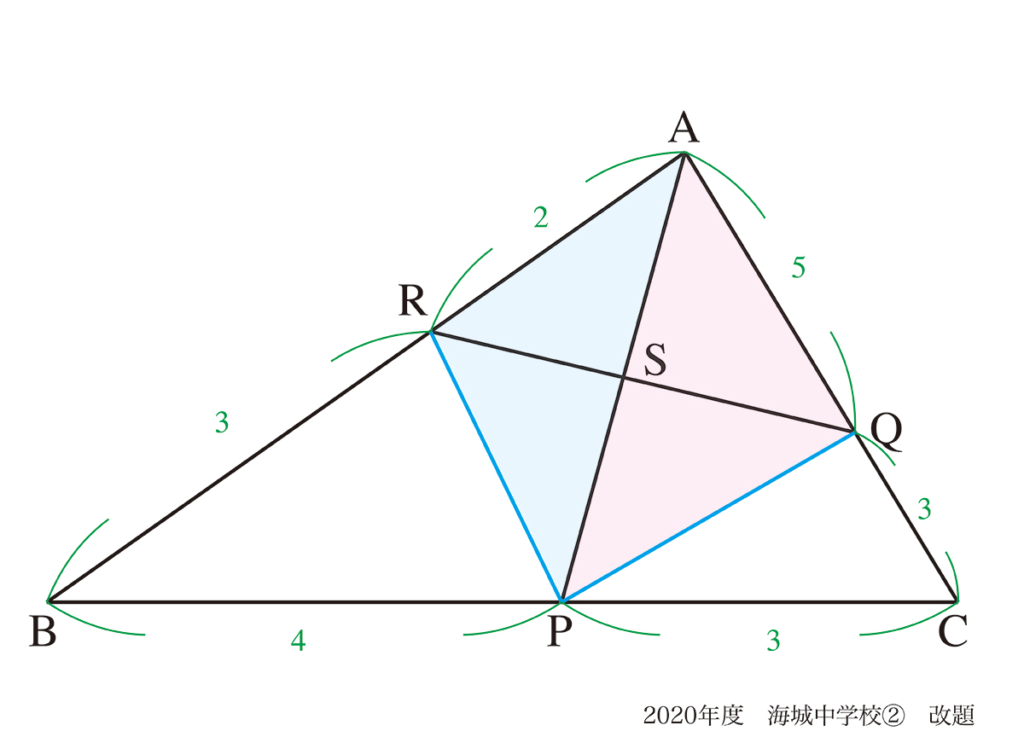
図形問題は「実際に手で描いてみる」ことが大事な話を、上記リンクでご紹介しています。

描いてみると「頭で考えていたら気づかないこと」に不思議と気づくことが多いです。

上の問題なら、「面積比」でも「辺の比」でも、描いて早く「解く鍵」を見つけることが大事です。

「解く鍵」をテンポ良く発見する考え方

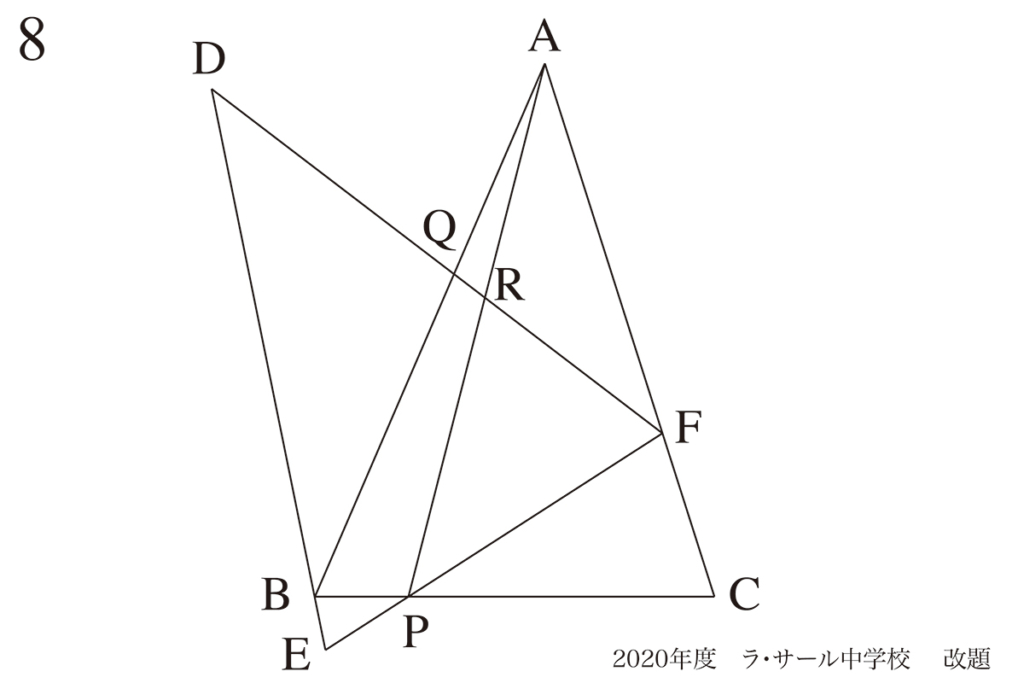
算数は「解く鍵」が必ずあります。

この「鍵」は図形問題では「分かりやすいようで分かりにくい」こともあります。

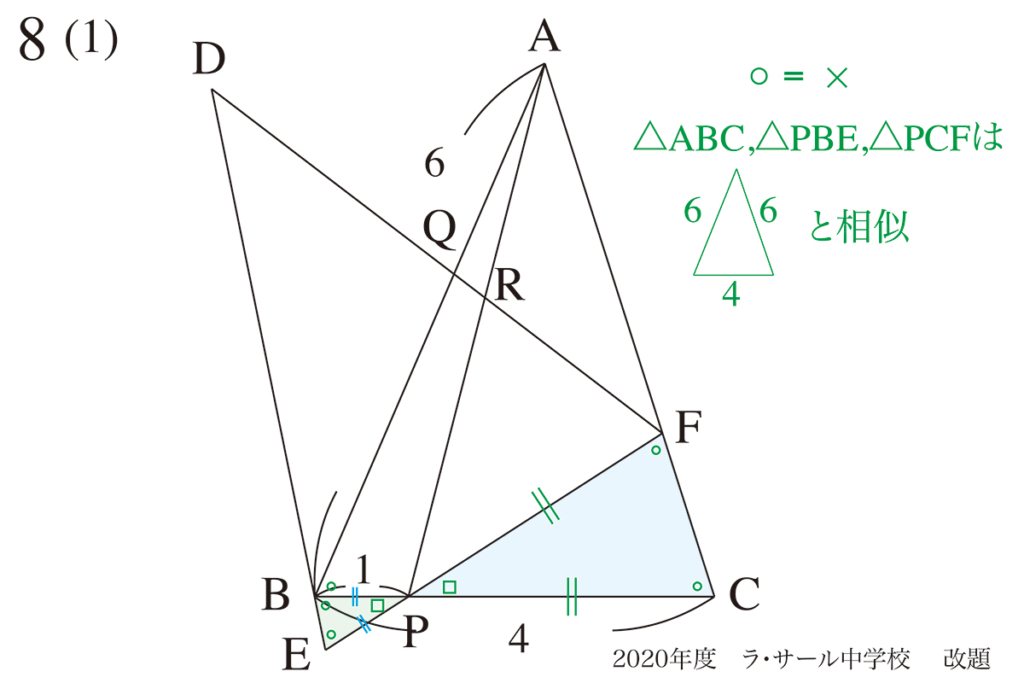
図形を回転したり、折り返す問題のコツを、上記リンクでご紹介しています。

丁寧に同じものを書き込んでゆくと、分かりやすいです。

多くの受験生がやっていると思いますが、「分かることを書き込む」と理解が進みます。

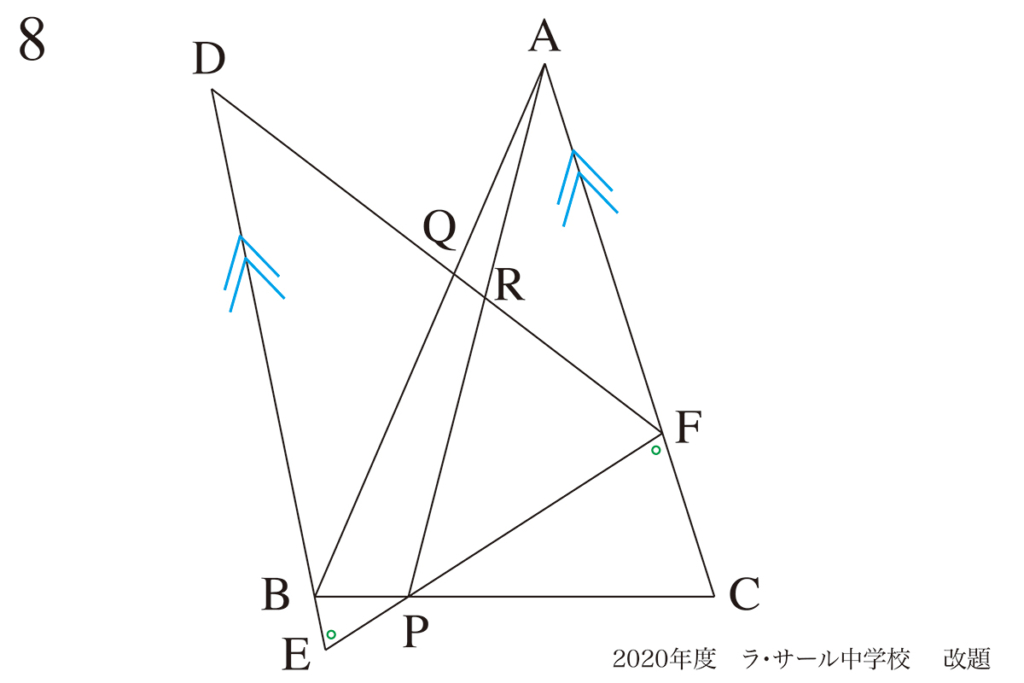
図形問題は「分かること」を描きこんでいくと、「平行や相似形が発見できる」ようになります。

平行な線が見つかったり、平行な線を補助線にすると一気に相似形が見えてきます。

平行な直線と角度に関しては、その「性質」をしっかりと頭に入れて理解しましょう。

「平行な直線」が図形問題のポイントであることは、受験期後半〜直前期の受験生なら、

「分かっている」と感じるかもしれませんが、もう一度「平行とは何か？」を改めて復習しましょう。

そして「平行であること」の性質をもう一度考えると、「見えてくる」ことがあるでしょう。

対称な図形の中心は「へそ」：異なる視点で見て考える

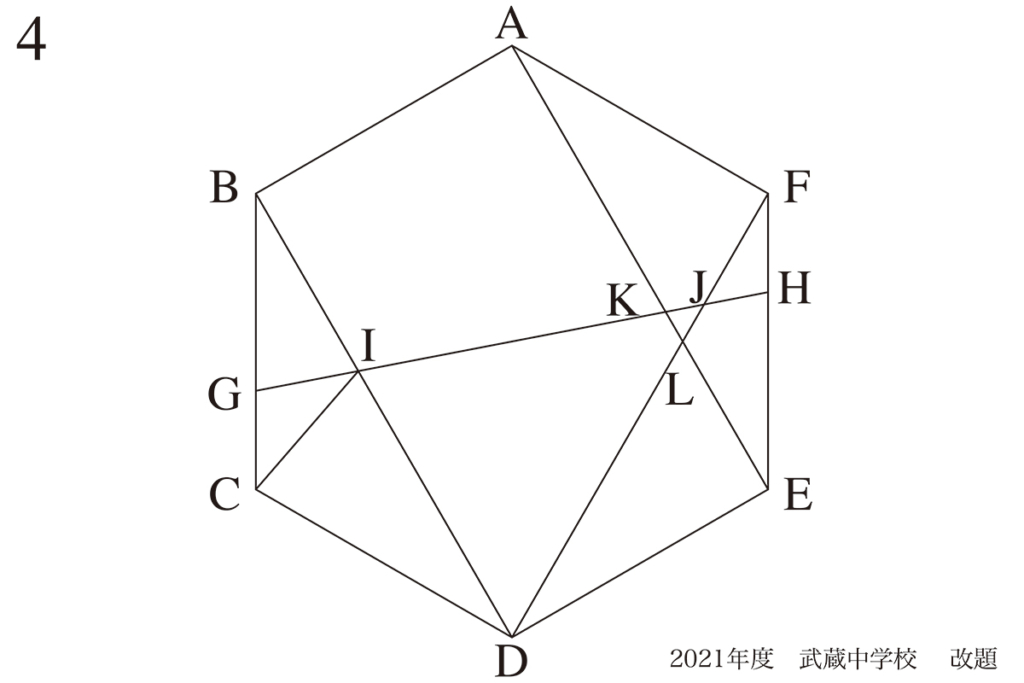
あるいは正六角形や正三角形が出てきたら、非常に特徴的な性質が多いです。

正方形・正三角形など「正〜角形」のように対称性のある図形・円は、中心に注目しましょう。

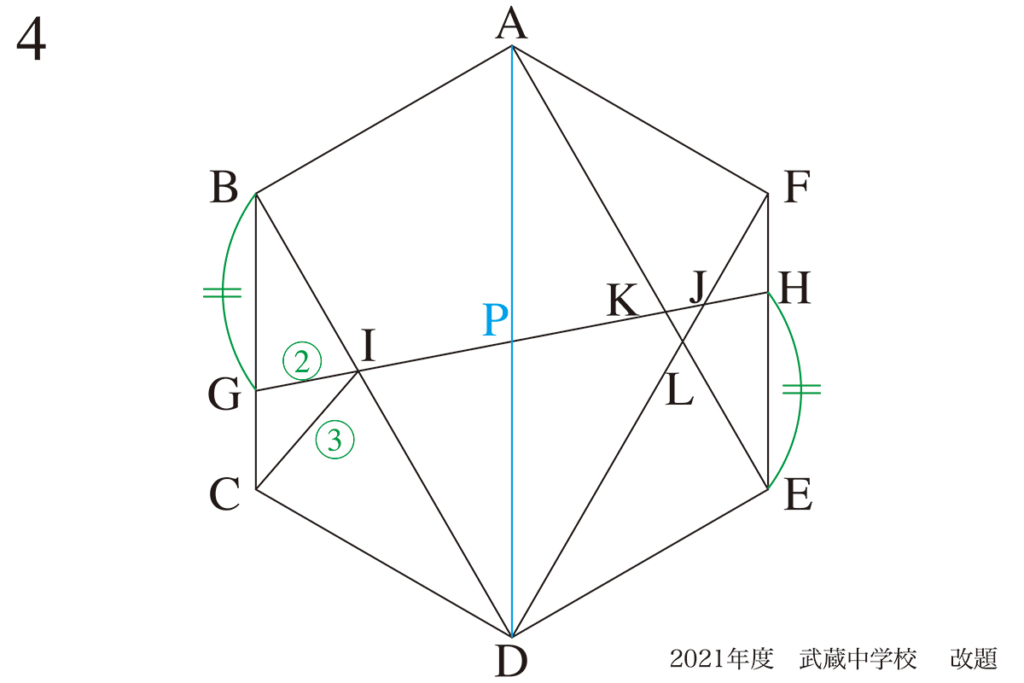
これらの「対称性のある」非常に特殊な図形の「中心」は、図形の「へそ」にあたります。

図形の「へそ」を押さえることが出来れば、一気に問題が見えてきます。

それらの「特徴的性質」をきちんと考えて、図形に描き込んでゆきましょう。

正六角形の問題を解くコツを、上記リンクでご紹介しています。

図形問題では「平行」は非常に大事なポイントになります。

平行な直線があると、相似形が次々と見えてきます。

問題の図形においては、

「平行な直線のペア」を探す考えるのも良いでしょう。

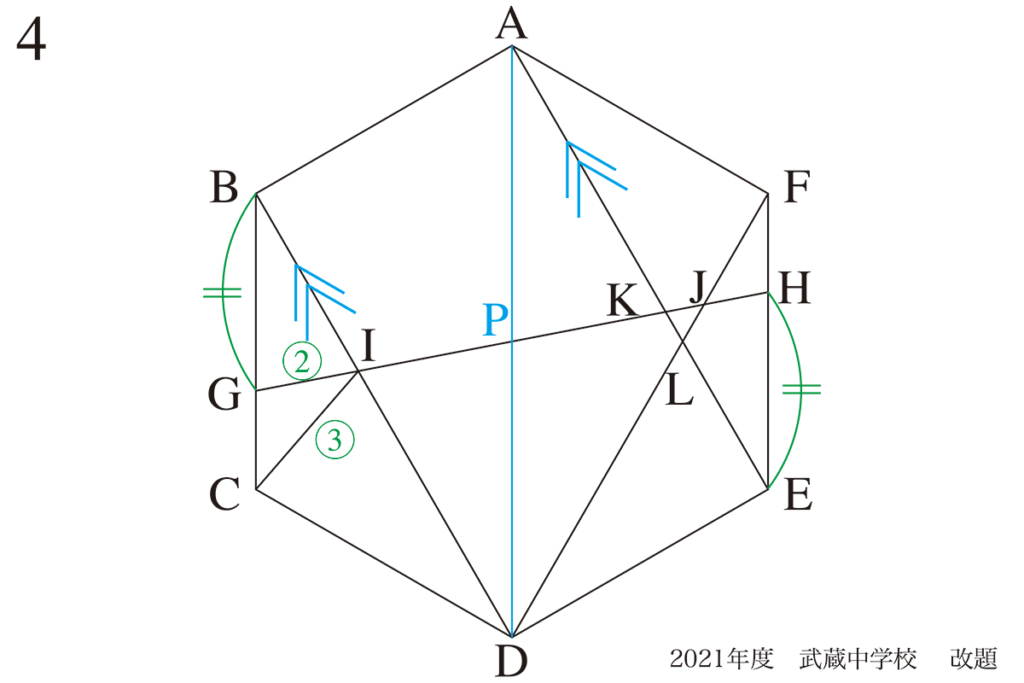
正六角形などは、図形の中の直線に「平行な直線の組み合わせ」がたくさん出てきます。

図形の見方を少し回転させたり、斜めから眺めてみる話を上記リンクでご紹介しています。

このように異なる視点で見てみると、「新たなことに気づく」ことがあります。

試験では、こうした「解く鍵」を「短時間にパッと探して、発見できる」ように心がけたいです。

そのためには、受験期後半〜直前期の学びの際には、

「解く鍵」や「大事なポイント」を、これまで以上に強く意識して勉強すると良いでしょう。

次回は下記リンクです。