前回は「文章題の内容を具体的にイメージして学力アップ〜比が出てきたら未知数設定・簡単な絵やメモを書く・「分かっていること」を表現・木を見て森も見る・問題 7(2)解法〜」の話でした。
目次
回転移動する図形の考え方

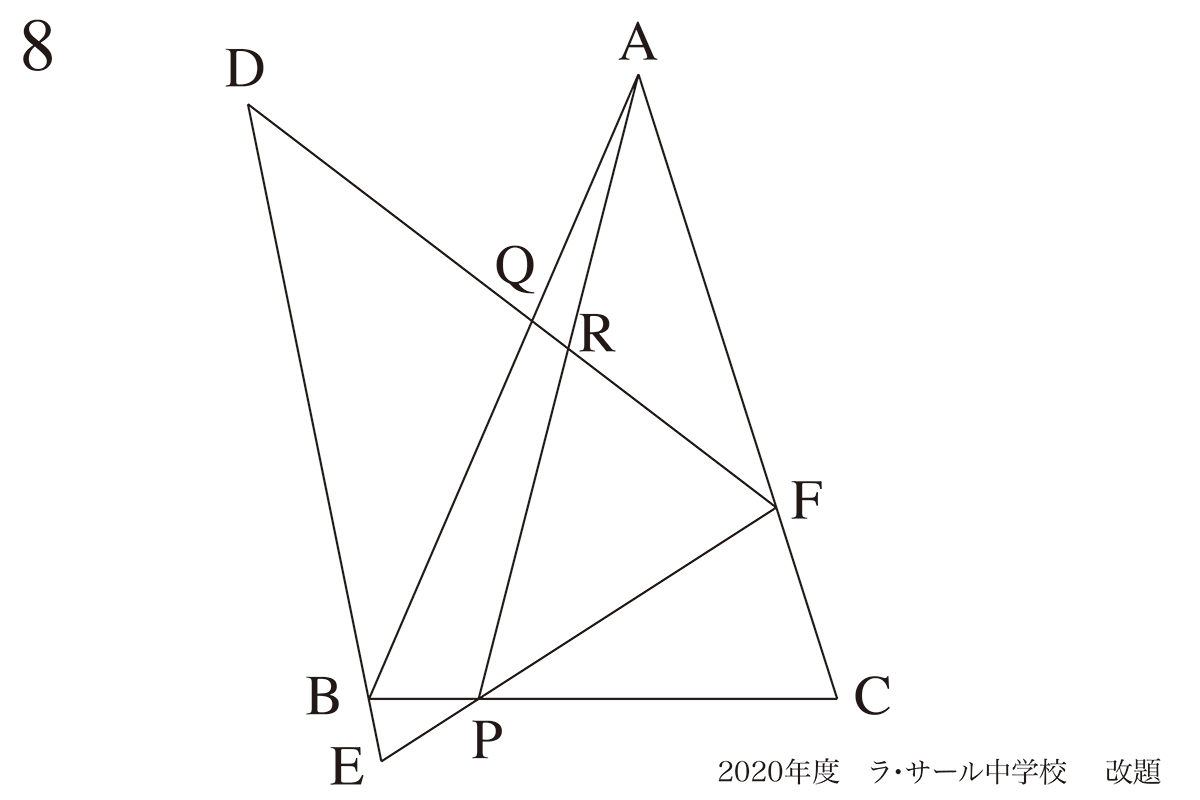
今回は、図形問題の問題8です。
図形を回転させる問題で、ラ・サール中学校の問題を改題しています。
(1)(2)は同一で標準〜やや難、(3)(4)はやや難の問題です。
図形問題の様々な要素が入っており、まとめにちょうど良い問題です。
考え方・解法は次回ご紹介します。
回転すること:同じ図形が2つあること

上の図形は一見すると「少し不思議な形をした図形」に感じられるかもしれません。
元々は「点Pを中心に図形を回転」なので、大事なことは「同じ図形が2つあること」です。
 男子小学生
男子小学生それは分かっているけど、
こういう問題って、難しい・・・
「同じ図形が2つ」なので、「それほど難しくない」はずなのに難しく感じられます。
それは、「同じ図形でも、角度が違う(回転している)と違うように感じられる」からです。



確かにそう・・・
「同じ三角形」のはずなのに、違って見える・・・
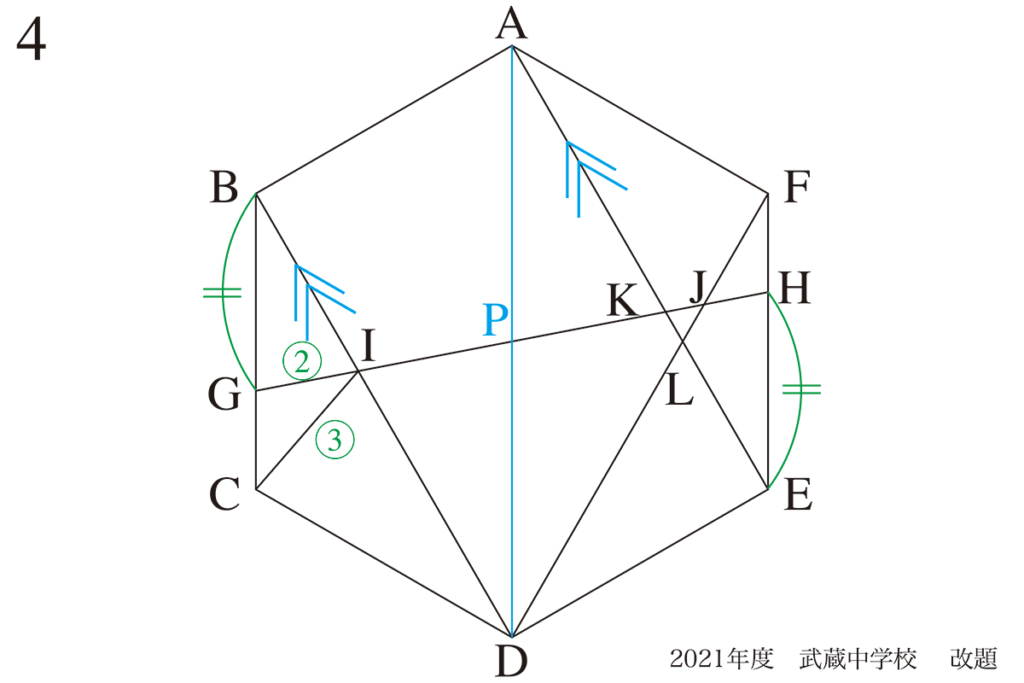

正六角形で「平行な二つの辺」を考えるとき、
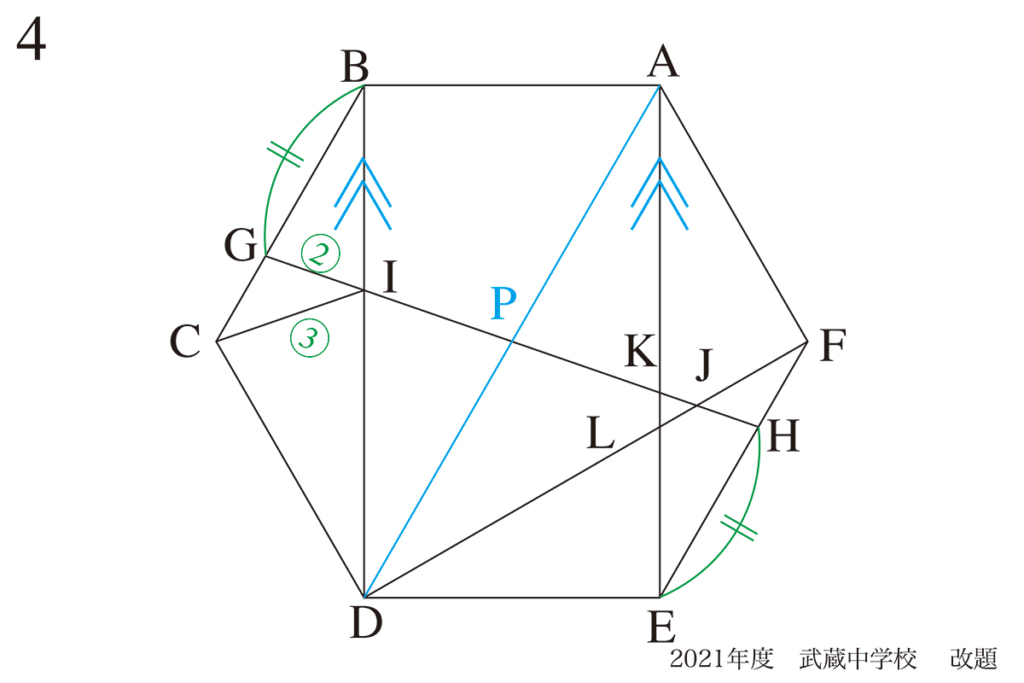

正六角形の中央(中心)を中心に、30度右に回転させると「すぐに分かる」話をご紹介しました。(上記リンク)
この時は「図形全体を自分で回転」しましたが、今回は「図形を回転させて重ねる」問題です。
「回転させる」と「違う図形」に感じられますが「同じ図形」です。
「同じ図形」ですから、「同じ長さ・同じ角度」が沢山あります。
これは「当たり前のこと」かもしれませんが、非常に大事なことです。
回転図形を考えるポイントは「同じ図形であること」を強く認識することです。
次回は下記リンクです。



