前回は「算数の成績アップ勉強法〜基礎力を応用力に転換・算数の難問が解けるようになるコツ・「分からない」から「分かる」へ・暗記の学力と勉強時間・算数の学力と勉強時間〜」の話でした。
算数が「できない子」ができるようになる勉強法
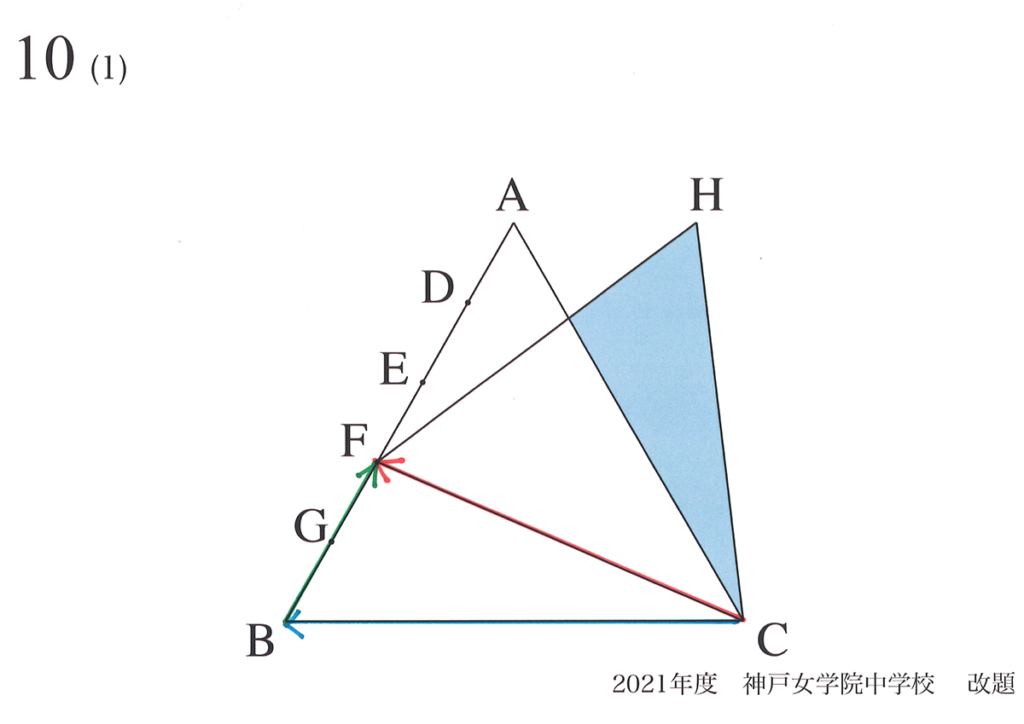
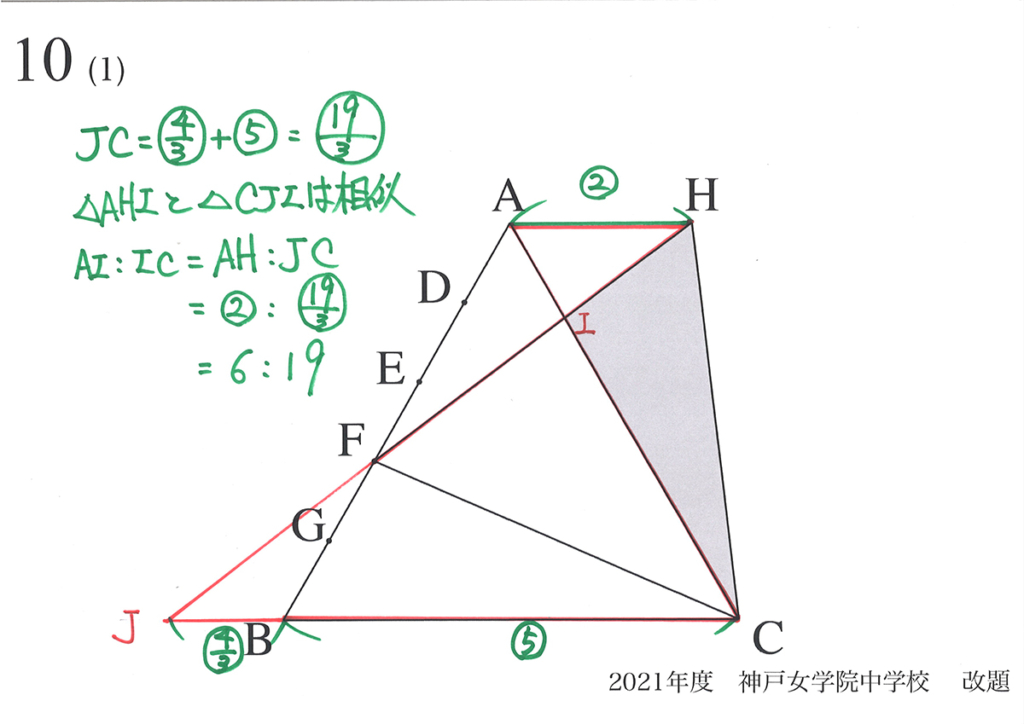
問題10で「動く点に合わせて、新たな正三角形ができる」問題を考えました。
この問題は非常にシンプルで、正三角形の性質が分かる大事な問題です。
ここでは「矢印の考え方」の話をご紹介しました。
・「ある点から複数の異なるルートである点に移動する」ことは、元の位置関係は同じ
・「ある点からある点へ異なる辺を移動する」ことは、図形的な位置関係は同じ
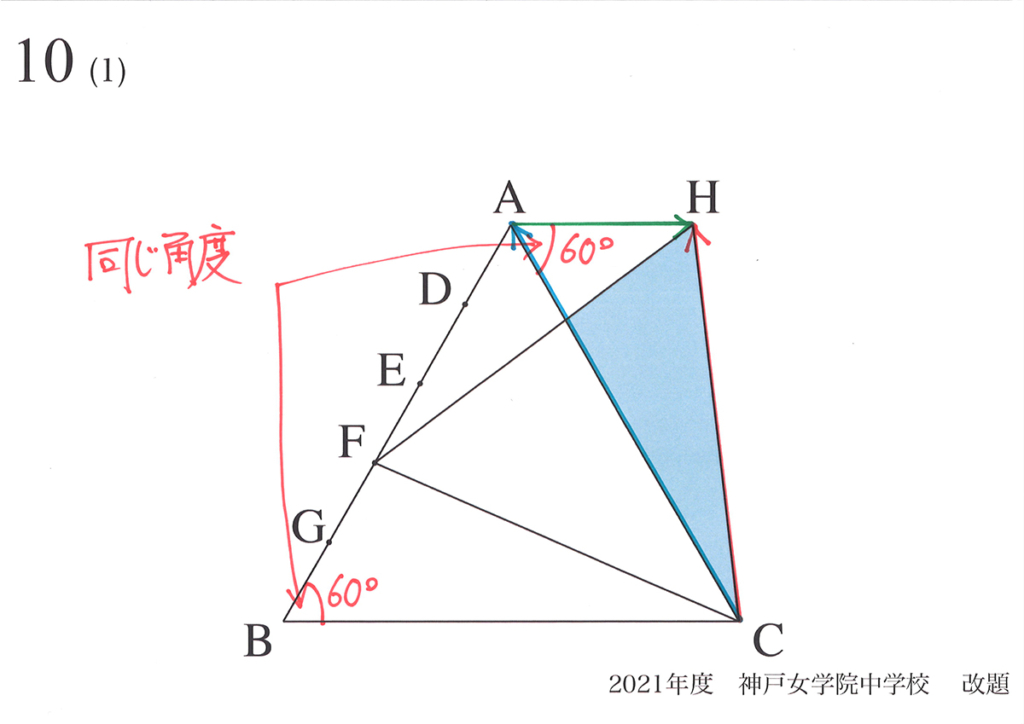
シンプルで奥が深い問題は「良い問題」です。
塾のテキストなどにも掲載されている可能性が高いので、
あっ、
この問題は塾でやったことあるよ！
こことここが
同じで・・・
という感じで「解ける」方がいると思います。
何度か問題を解いているうちに、
解き方を
覚えちゃったよ・・・
という方もいるでしょう。
やったことのある方は、「きちんと解けるか」を確認することが大事です。
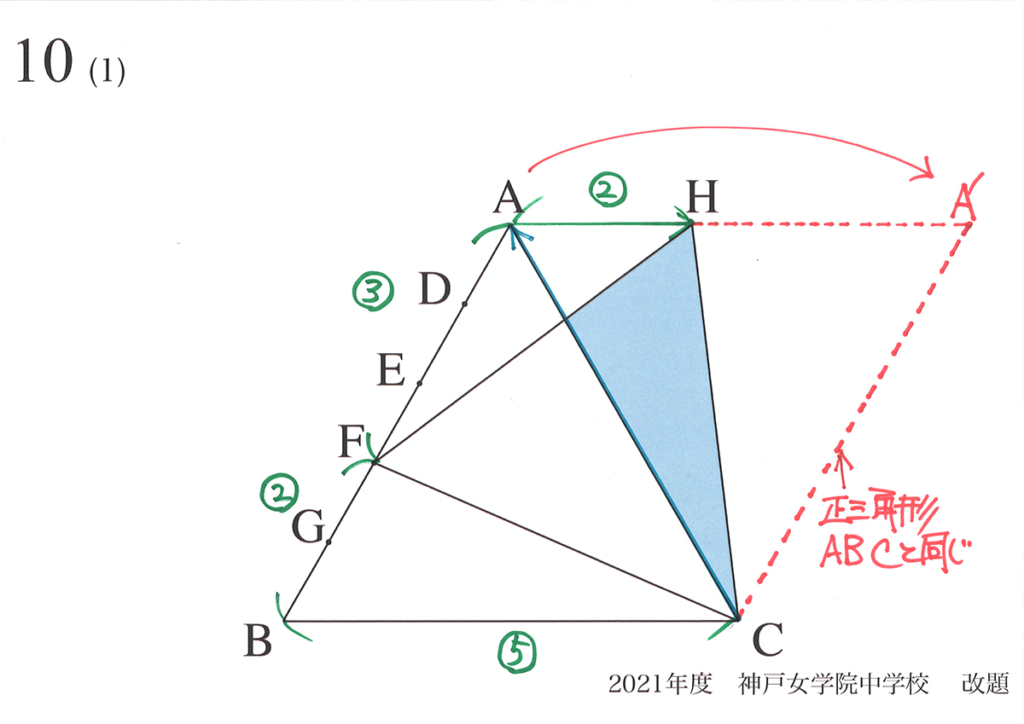
矢印CFを回転すると、矢印CBが矢印CAに、矢印BFが矢印AHに移ります。
矢印を回転して正三角形HFCを作ると「矢印BFが矢印AHにちょうど重なる」ことが分かれば解けます。
ここがこの問題の最も大事なポイントです。
「やったことがあるかどうか」も大事かも知れません。
「やったことがある問題の考え方を理解していて、自分で解けること」がより大事です。
・取り組んだ問題の大事なポイントをしっかり理解
・解き方や考え方をしっかり習得
一度やった問題がもう一度出たら「しっかり出来る」こと：「上がらない」から「上がる」へ
この図形問題は、正確でなくて良いので正三角形などを自分で描くと良いでしょう。
そして、「分かったこと」を図形に描きこんでみましょう。
・求めるものが「面積・長さ・角度」など何でも、まずは「図形の性質」を考える
・点と点を結んで、矢印を考えて「図形の位置関係」を考える
・分かった図形の大事な性質を図形に描きこんで考える
「一度やった問題をしっかり理解すること」が大事です。
そして、「一度やった問題がもう一度出たら、しっかり出来る」ことを目指しましょう。
特に小学校6年生の後半の時期は、問題数よりも「着実に習得」を目指しましょう。
たくさん問題を
解いているけど・・・
もう一回やってみたら、
出来なかった・・・
にならないようにしましょう。
算数は特に「一つ一つきちんと理解して進む」をぜひ実行して下さい。
大事な性質や鍵をもう一度考える姿勢：「遠回り」が「近道」
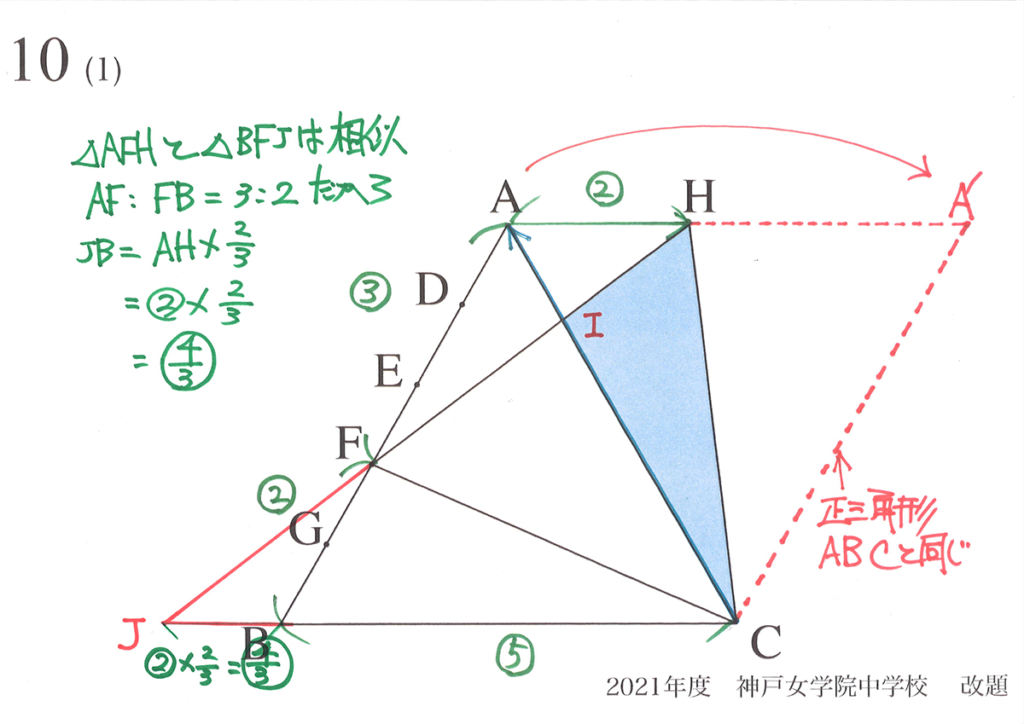
この図形問題を解くとき、大事な性質があります。
それは、「辺AB上のどの点をもとに新たな正三角形を作っても、AHとBCは平行」です。
そして「上の図でBF=AH（同じ）」ことも大事です。
「やったことがある」方は「それらの性質を覚えていて」解けたかもしれません。
あっ、これはこの線と
この線が平行だったな・・・
と、「解いているうちに覚えた」ことも学びの一つです。
「ある性質を覚えている」ことは良いですが、それを「既知のもの」として解かないようにしましょう。
「解いたことのある問題の大事なこと・性質」を覚えていたら、
そういえば、
これはなぜだったかな？
ともう一度考えましょう。
これらのことは、先ほどの「矢印の話」で一度に解ります。
「矢印の話」以外の方法でも良いので、きちんと理解しているかを確認しましょう。
ここで、「もう一度考えてみる」ことは、なかなかやらないことかも知れません。
だって、もう一度そういうことを
考えたら時間かかるし・・・
やらなければならない
問題が沢山ある・・・
受験生の後半は「やらなければならない事が山のようにある」ように感じられます。
すると問題を解く「質よりも量」に向かってしまう傾向があります。
理科・社会の暗記問題は「量も大事」かも知れません。
算数の特に応用問題は「きちんと理解して、一つ一つ進む」ことを目指しましょう。
でもさ、もう一回考えて、
解けない補助線引いても意味ないんじゃない・・・
もし、「もう一回図形問題を考えて、解法に至らない補助線を引いた」時。
それは「無駄ではない」のです。
「解法に至らない補助線」を引いたときは、
この補助線は、なぜあまり
有効ではないのかな・・・
と考えて、「解法に至る補助線」と比較する姿勢は大事です。
・「解法に至らない補助線」と「解法に至る補助線」を比較
・図形問題以外でも出来なかったときは、「何が良くなかったか」を考える
このように「解法を比較する姿勢」は大事です。
あまり長い時間を掛けなくてもよいので、少しの時間考えてみましょう。
すると、
あっ、
これはここが分からないな・・・
だから、
解法に至らなかったんだ・・・
と分かるようになります。
・解答に至らない「無駄なこと」が大事
・「遠回り」や「無駄」を経験すると、試験で「何が大事か」の感覚が磨かれる
そうして地道に「一つ一つ考え方をきちんと理解してゆく姿勢」が、最も大事です。
それこそが、特に算数の難問が解ける学力アップへの「遠回りなようで、最も確実な近道」です。
