算数・理科が「出来ない」から「出来る」へ〜「考え方を理解」することを大事に・描いて理解する姿勢・まずは描いてみる・実体験をイメージして理解力アップ・感性を大事に〜｜中学受験・高校受験・大学受験

前回は「早めに過去問を解く大事さ〜「過去問はいつやるべきか」に対する様々な考え方・合格目指して一歩でも二歩でも踏み出す姿勢・まずは過去問・各学校の教育方針とカラーが強く反映される入試問題〜」の話でした。

算数・理科が「出来ない」から「出来る」へ：「考え方を理解」することを大事に

今回は中学受験の算数を具体的な例としてお話しします。

受験に向けての姿勢として、高校受験〜大学受験の数学等にも共通する点があるでしょう。

もうすぐ4月を迎え、正式に「受験生」となる現在小学校5年生のみなさん。

すでに気持ちは

かもしれません。

1990年に中学受験した僕は、週に一回のテストの教室に小学校4年の12月から通っていました。

夏期講習等には行っていましたが、本格的に塾へ行き始めたのが、小学校5年の2月です。

つまり、来年中学受験する予定の皆さんからみると、先月の2月から塾に行きました。

当時も「ちょっと遅め」だったかもしれません。

それだけに最初は「大変な思い」をしました。

2月の最初の土曜日に学習指導会の「武蔵特訓」に行った時の衝撃は、いまだに覚えています。

周囲の皆が知っている「てんびん算」を「知らなかった」僕。

数ある中学受験算数の「考え方」や「解き方」の中で、最も本質的である「てんびん算」。

考え方は非常にシンプルです。

「てんびん算」の考え方は「面積算」とも共通する点があります。

いずれの場合も、「解き方を覚える」よりも「考え方を理解する」ことが大事です。

描いて理解する姿勢：まずは描いてみる

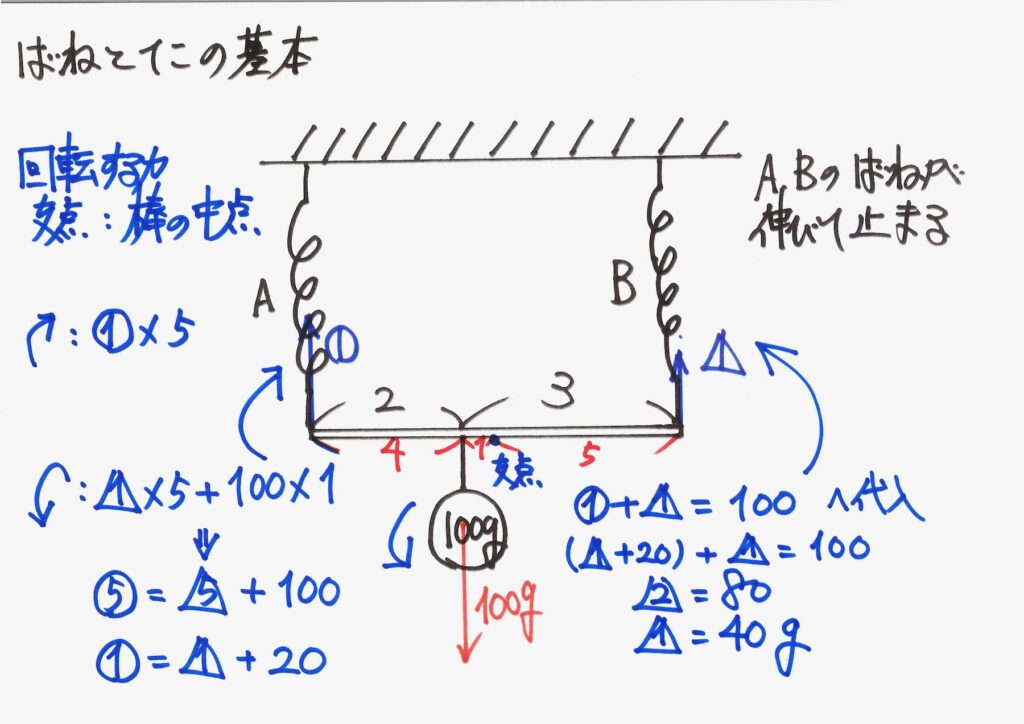
算数や理科で、

と悩んでいる方も多いと思います。

「てんびん算」の考え方・解き方は、4月から小学校6年生の中学受験生の多くの方が、

でしょう。

もし、今この時期に、

という方も、ガッカリしないで考え方を理解してみましょう。

「てんびん算」の基本は、「てんびんの釣り合い」で算数と理科に共通します。

「てんびん算」と考えると「算数の勉強」と考えがちですが、「理科の勉強も兼ねている」と考えましょう。

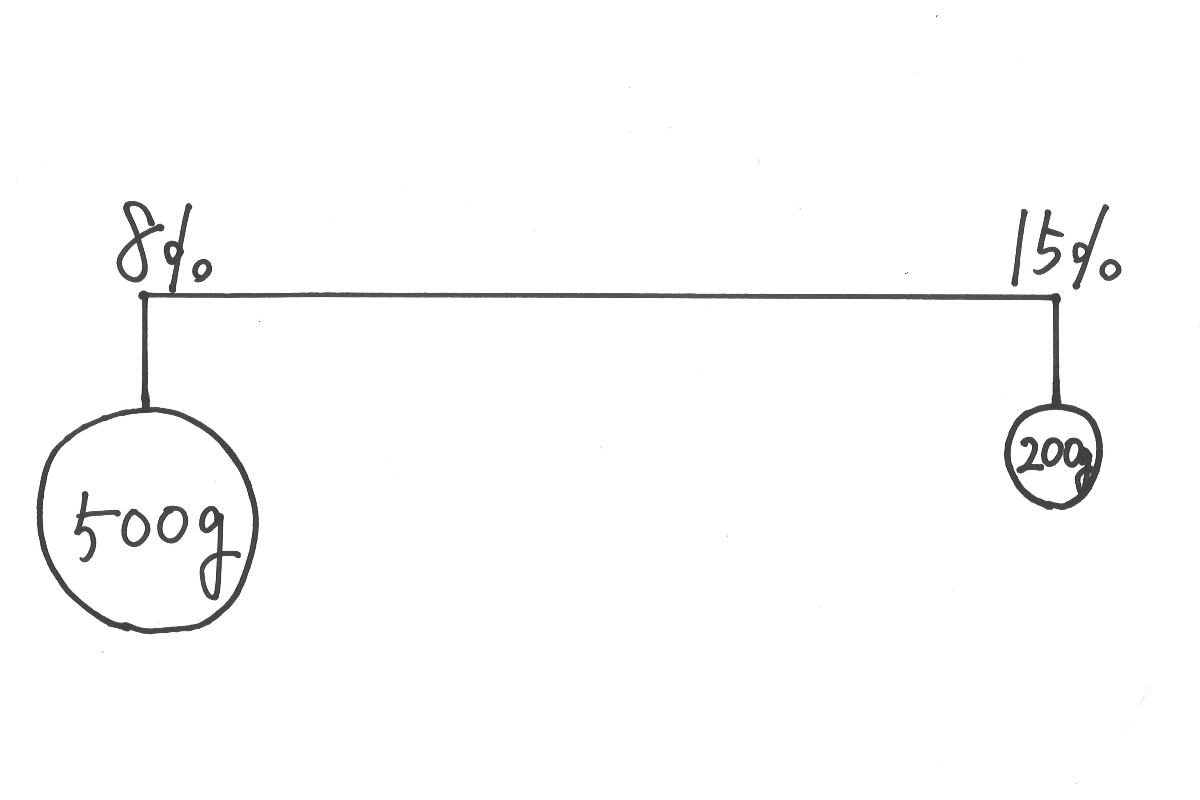
「てんびん算」を考えるときは、必ず「てんびん全体を大きく描く」をやってみましょう。

慣れてくると「食塩水のかたまり」として「吊り下げるボール」の大きさは「同じくらい」で描く方もいるでしょう。

あるいは、「食塩水の量に応じて大きさ・サイズを変える」方もいるでしょう。

慣れればどちらでも良いです。

初期の頃は、「食塩水のかたまり」=「吊り下げるボール」の大きさは変えましょう。

上の図は「少し誇張して描いて」いますが、これくらい違う風に描いても良いでしょう。

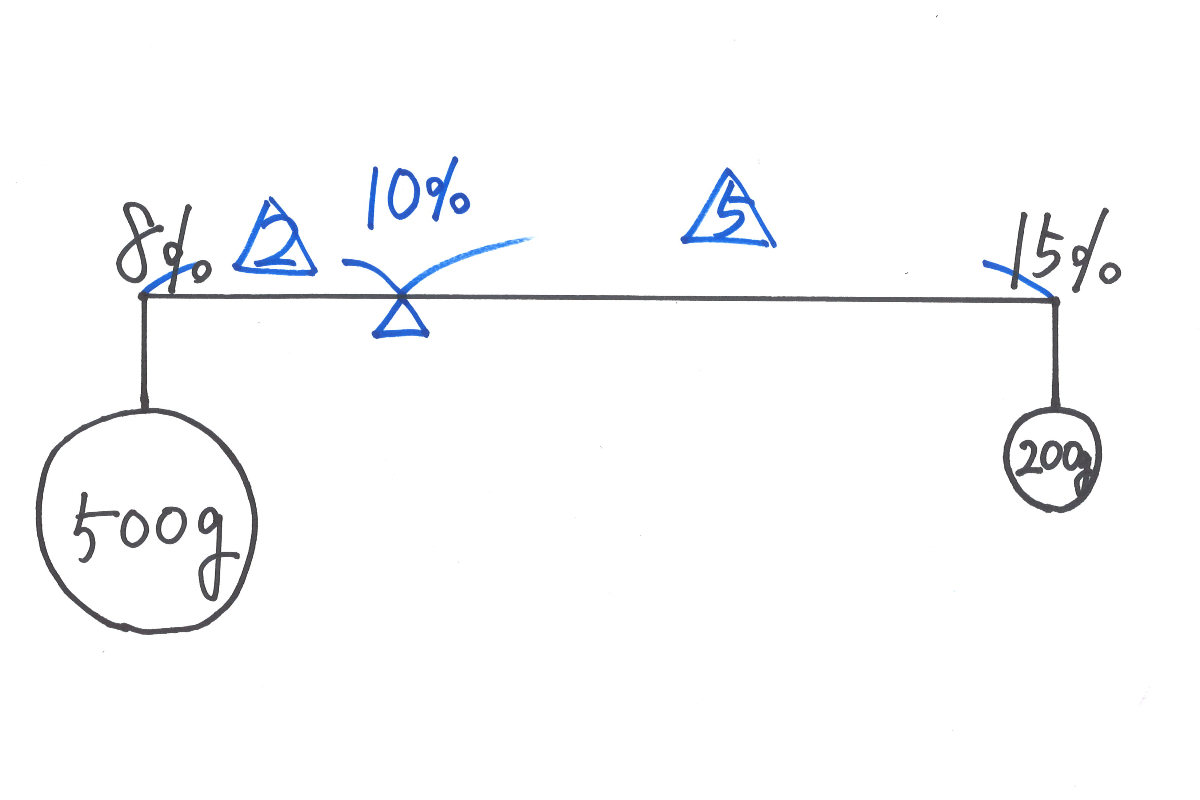
こうして「バランスをとる」ことを考えてみれば、単なる「解き方・解法」から「感覚的に理解できる」ようになります。

実体験をイメージして理解力アップ：感性を大事に

昔は小学校の授業で、上皿てんびんで「実際に計量する」実験をやりました。

最近の小学校でもやっていると思いますが、状況は分かりません。

上皿てんびんで計量したことがある方は分かりますが、「ピタッと計量」するのは結構難しいです。

という経験は誰しもあります。

こういうのは「映像・動画で見れば、分かる」のですが、「実体験する」とは全然異なります。

「てんびん算」でも、「ばね・てこの問題」でも、「上皿てんびんの体験」を思い出してみてはどうでしょう。

すると「釣り合う感覚」が体験できます。

その「感覚」を抜きにして、ひたすら

と考えると楽しくなくなってしまい、理解が進まない場合があります。

「算数・理科の問題に取り組む」姿勢の時に、こういう体験をイメージすると総合力が上がるでしょう。