前回は「「伸びない・解けない」から「伸びる・出来る」勉強法〜条件を明確化・いくつか補助線を引いてみる姿勢〜」の話でした。
思考の流れと「考え方の引き出し」の整理
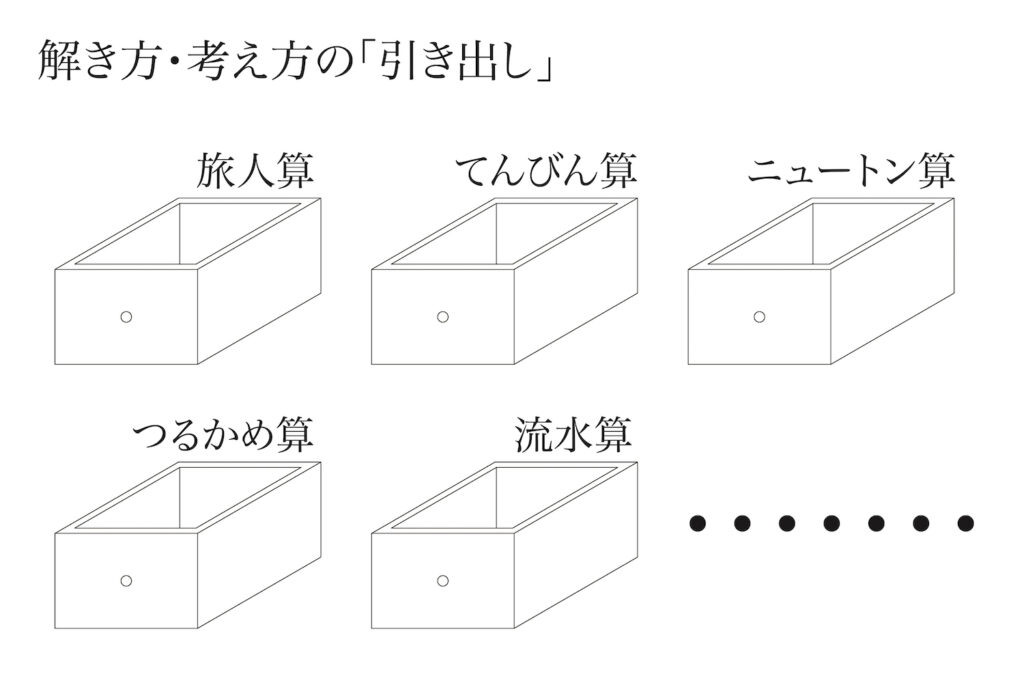
難問を解くには、これまで学んだ解法をしっかり理解・整理することが大事です。
上のように旅人算・てんびん算・・・などのたくさんの分野の算数を学びます。
さらに、それぞれの分野において解法・テクニックがあります。
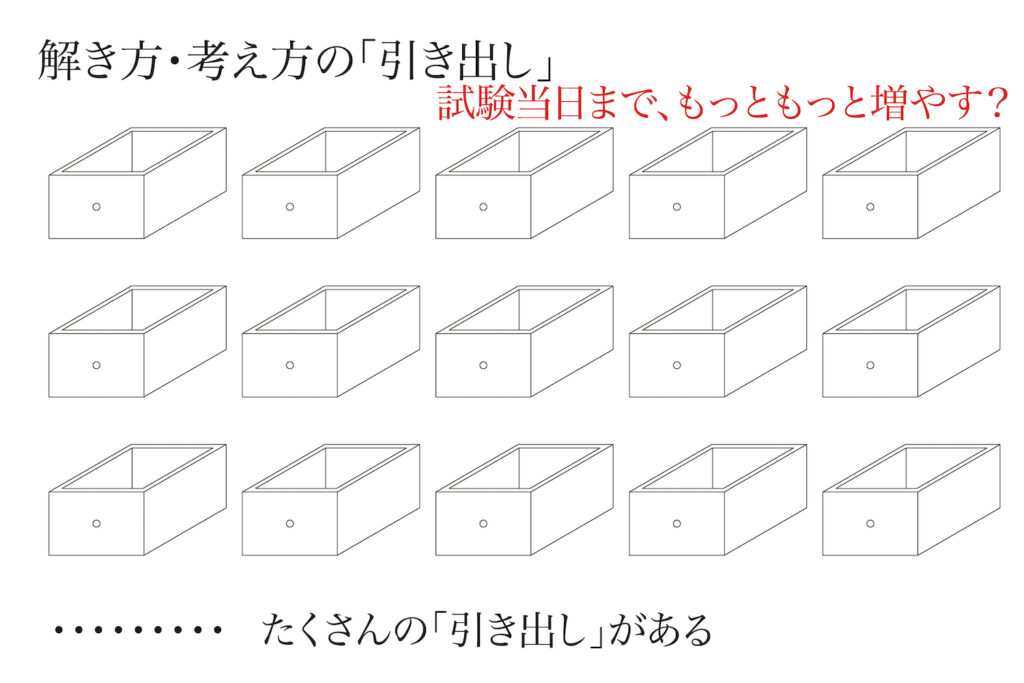
これらの「大きな解法」の中にさらに細分化された「小さな解法」が頭に蓄積されてゆきます。
模試などで、
男子小学生あっ、この問題
出来なかった・・・
男子小学生やっぱり、もうちょっと
「解法パターン」を頭に入れないと・・・
このように感じて、一生懸命勉強してみると、
男子小学生あれっ、この間出来るようになったはずの
「解法パターン」があやふやになった・・・
女子小学生あの解放パターンを
忘れてしまった・・・
「新しいことを学ぶと、出来ていたはずのことが出来なくなる」こともあります。
理科や社会では、こういうことは比較的少ない傾向があります。
ところが、応用問題や難問に取り組む受験生にとって、算数は、
女子小学生出来るようになったと
思ったら、また出来なくなった・・・
実に色々な問題があり、それらに一つ一つ対応することは「モグラ叩き」みたいになってきます。
女子小学生確かに
モグラ叩きっぽくなってるかも・・・
解法の問題を解く際には、「過去に解いた解法の引き出し」を利用する考え方になる傾向があります。
本質的に考えるためには、もっと基本的な「大きな引き出し」から考える方が望ましいでしょう。
ところが、「短時間で多数の問題を解く」必要がある受験生は、どうしてもこの傾向があります。
いわば、この「解法の引き出し」は「多ければ多いほど良い」のも現実です。
・「解法の引き出し」や「思考の引き出し」を増やす
・「解法の引き出し」は増やすことが目的ではなく、増やしながら整理
ところが、一生懸命「たくさんの解法の引き出し」を蓄積すると、
男子小学生あれ？あの「引き出し」かな？
やっぱりあっちの「引き出し」かな？
混乱してしまう可能性があります。
そのためには「解法の引き出し」あるいは「思考の引き出し」を、時々整理するのが良いでしょう。
男子小学生どうやって
整理するの？
上のように整然と「解法の引き出し」が頭脳の中に並んでいる方は、かなり算数・数学が得意なはずです。
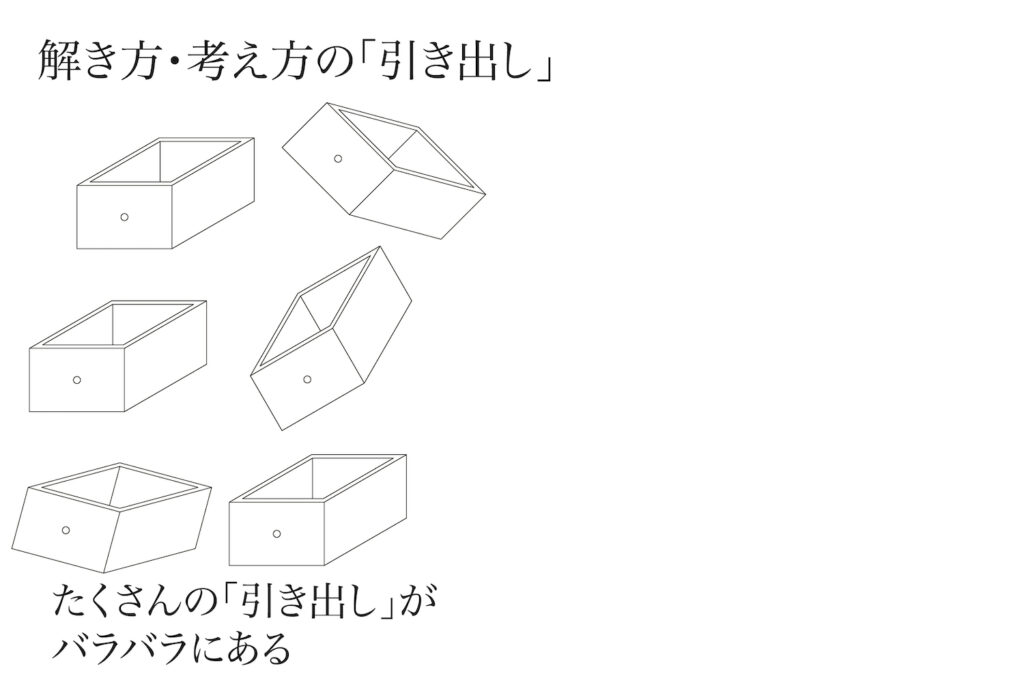
大抵の方は、上の図のように「解法の引き出し」がバラバラで整理整頓できていない状況です。
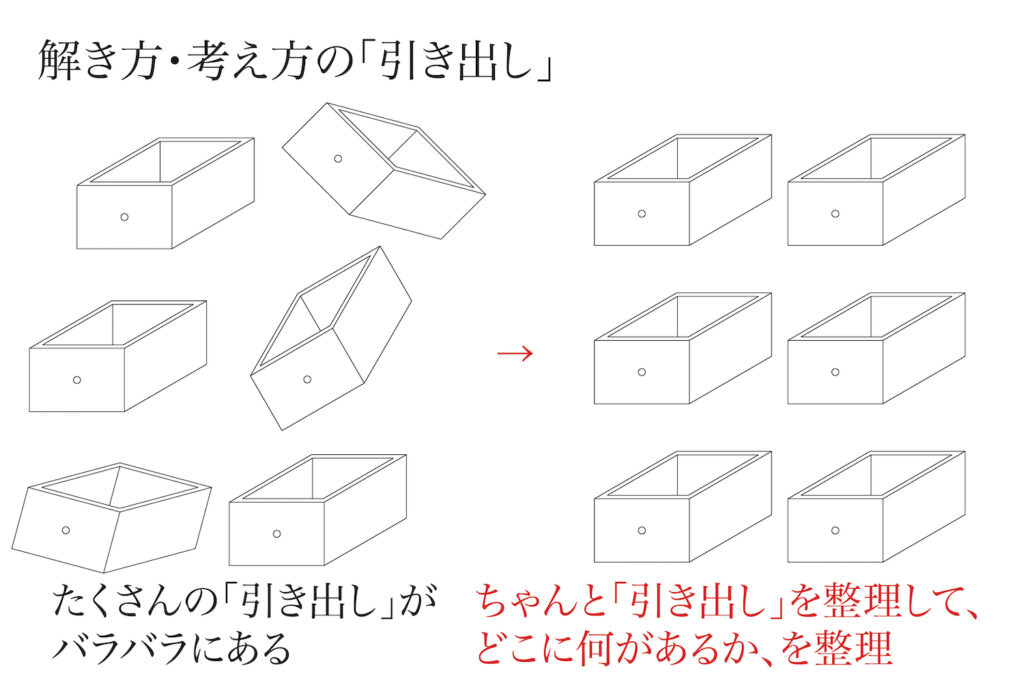
そこで「解法の引き出し」を整理整頓して、頭の中も整理しましょう。
特に小学校6年生の受験期後半は大事です。
このことは、中学生・高校生の数学や理科（特に物理）にも応用できる考え方でしょう。
難問が解けるようになる勉強法：なぜ「動く点を止める」のか
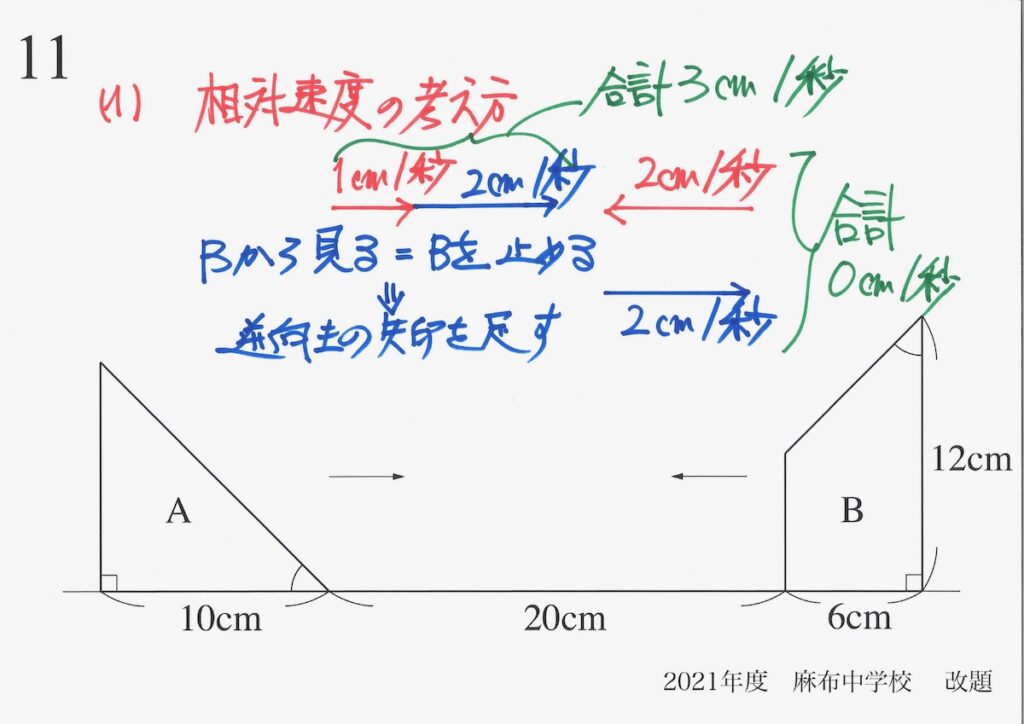
この「解法の引き出し」を整理することは、もう一度考え方を復習してみることです。
今までやった志望校の過去問などを、もう一度「初めてやる如く」やってみましょう。
上の問題のように「向かい合う点」や「動く図形」の時は、
男子小学生片方止めれば
いいんだよね！
女子小学生とにかく、動く点や図形が2つ以上あったら、
「片方止めて考える」と習った！
動く点・図形が複数ある時は、「片方止める」のが鉄則です。
それでは、なぜ「動く点は片方止める」なのでしょうか。
そして、なぜ「動いている点を止めて良い」のでしょうか。
そもそも、「動いているから考えにくい」ものを「勝手に止める」のは大丈夫なのでしょうか。
男子小学生確かに、
なぜって考えたことはなかったかも・・・
女子小学生「そう考えるもの」と
思ってた・・・
動く点・図形の問題をもう一度やってみて、
男子小学生二つの点があって、
同時に動くから・・・
「二つ動く」なら「片方止めなければどうなるか」考えてみましょう。
「相対速度（速さ）」の考え方を、もう一度復習してみましょう。（上記リンク）
・「こうすれば解ける」ではなく「こうしなかったら、どうなるか」を考える
・なぜ「こうすれば解ける」のか改めて考える
2つの点、あるいは3つの点が動く時は「どれかを止める」のが考えやすいです。
それでは、「どれかを止めなければ解けない」のでしょうか。
このように「難問の解法の理由」を、もう一度考えると学力が上がるでしょう。
それによって、「解法の引き出し」は整理されて、引き出しが大きくなるでしょう。
引き出しが大きくなると「たくさんのモノ（解法）が入っている」状況になります。
こういう引き出しが一つでも増えると、算数・数学は強くなるでしょう。
瞬発力鍛える勉強法：大問と小問への対応力アップ
一方で、受験では小問と呼ばれる「ちょっとした問題」や計算問題が出されるケースもあります。
単なる計算問題や、基本的概念でサッと「解けるはず」の問題です。
これらの問題は、基本的には「ある程度確保する」ことが合格には必要です。
大学受験では「単なる計算」は、積分計算などが多いです。
中学受験で時々見かける「複雑な数値を多数の四則演算で計算」する問題があります。
男子小学生ああ、ああいう問題は
僕の志望校結構出すよ・・・
「かなり複雑な計算」は、ちょっと間違えると、どんどん複雑になる傾向があります。
男子小学生結構、計算問題
間違えることがあって・・・
女子小学生この間の模試でも
間違えちゃった・・・
そういう時は落ち込まずに「毎日やって計算力を上げる」しかありません。
「思考力を問う」ならば大問3~4題程度が望ましいと思いますが、小問が沢山出る学校もあります。
そういう問題は、「テンポ良く、パパッと」解けるようにしましょう。
男子小学生そうなんだけどさ。
それが、難しいんだよね。
女子小学生パパッと出来たら、
苦労しないけど・・・
短い時間でパパッと出来るようになるには、「頭の良さ」よりも「トレーニング」の要素が強いです。
体育で大事な「反射神経が良い」は、生まれつきの個性の影響が強いと思います。
算数・理科などの「反射神経」は「頭の良さ」もありますが、ある程度は「努力で磨ける」です。
そのためには、「思考の流れ」を意識して考えると良いでしょう。
「流れをイメージ」して、歴史の理解を深める話をご紹介しました。（上記リンク）
算数でも、「解くプロセス・流れ」を意識しましょう。
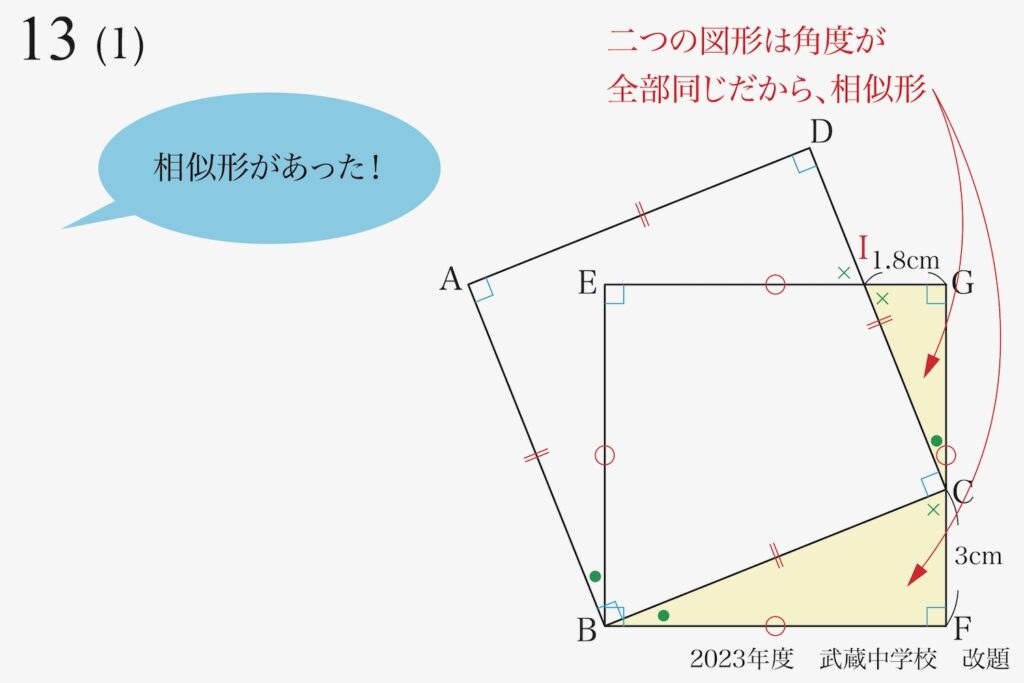
上の「正方形が二つ」の問題は、非常に本質的で良い問題です。
斜めの正方形が登場した時は、「外側に斜めの正方形を包む水平の正方形を作る」考え方もあります。
いずれにしても、「なぜ、解法のポイントとなる相似形は相似なのか？」をしっかり考えましょう。
「相似形を作り出す流れ」が、しっかり理解できることが大事です。（上記リンク）
すると「相似形を作る・見出す」ことが楽しくなり、どんどん解けるようになります。
今までやった問題をもう一度「なぜ？」と考え直すこと。
それは、応用力を大きく増進させ、ベストな難問対策になるでしょう。
次回は下記リンクです。
