前回は「重心・太さが一様でない棒：モーメント 2〜重心とつり合い・日常生活と重心・重心と回転する力モーメント・太さが一様ではない棒の重心・未知数への姿勢〜」の話でした。
「重ね合わせる」「ゆっくり引き上げる」と重心：異なる視点で考える
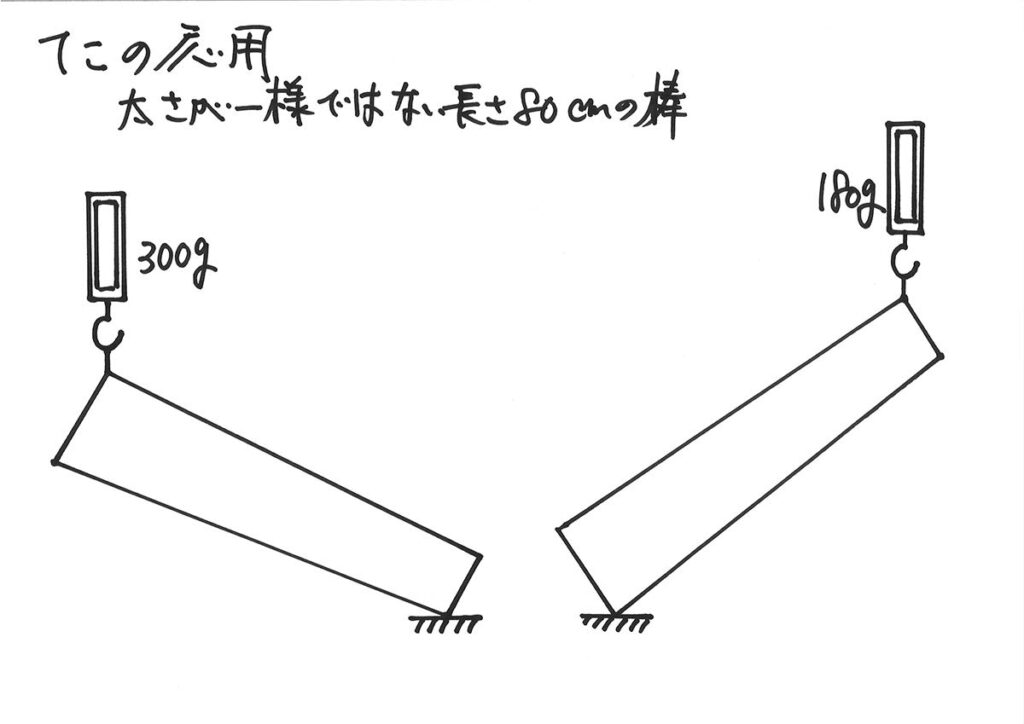
太さが一様ではない棒の左端・右端をそれぞれ引き上げている状況で、棒の重さを求める問題。
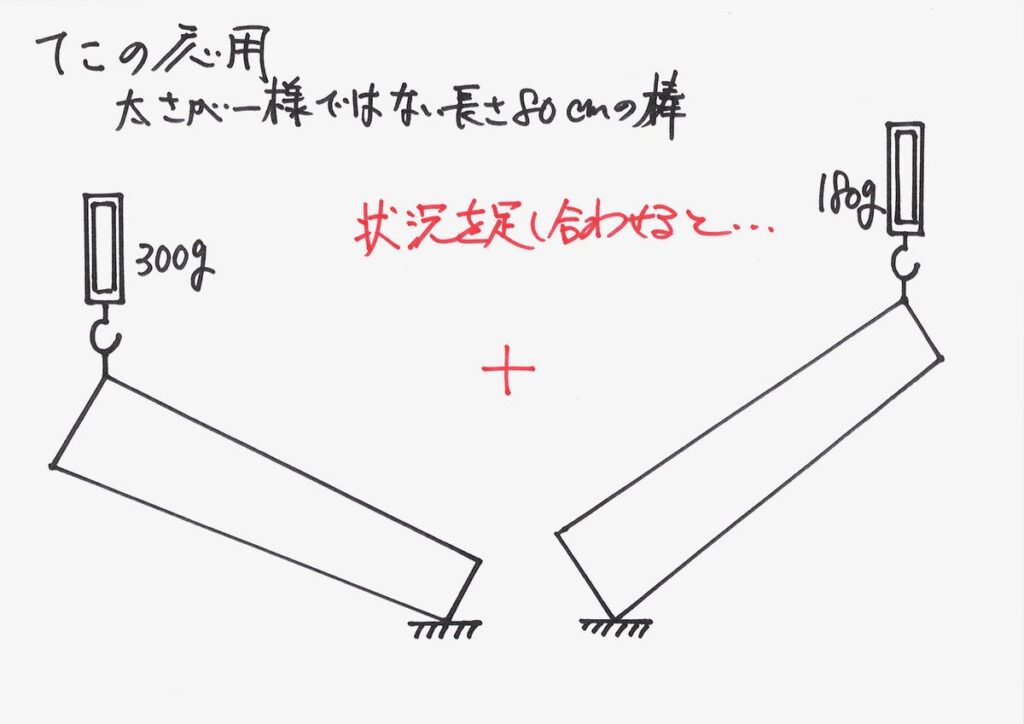
状況を「足し合わせる」「重ね合わせる」ことを考えてみましょう。
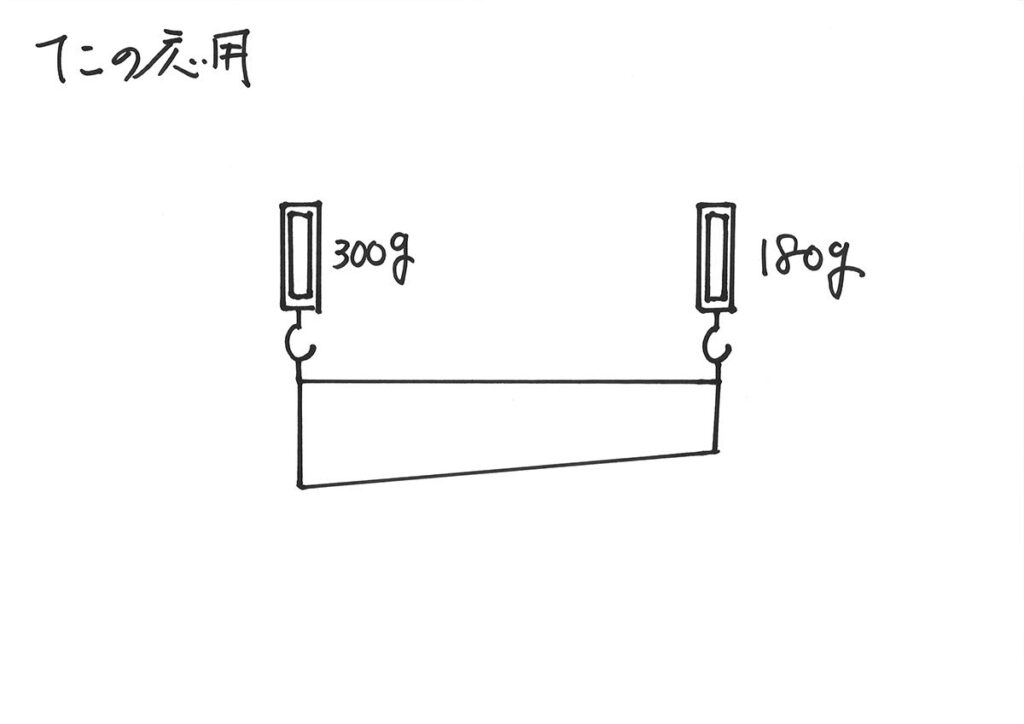
太さが一様ではない棒を「左右で引き上げ、つり合った状況」になりました。
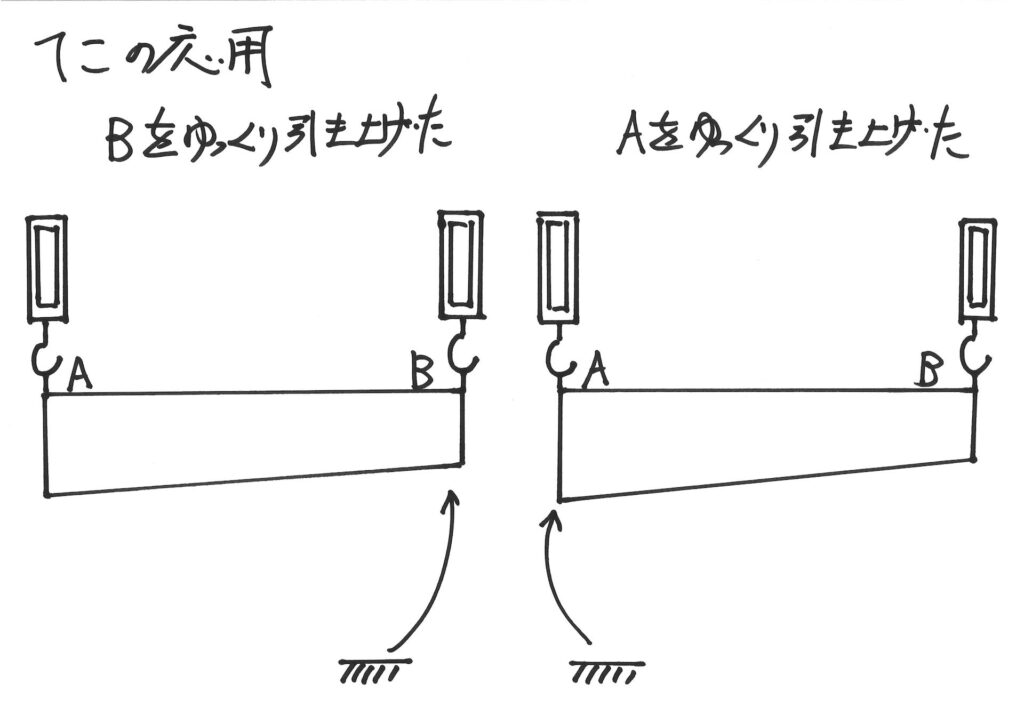
あるいは、「引き上げている反対側をゆっくりと、つり合いを保ちながら、引き上げる」考え方。
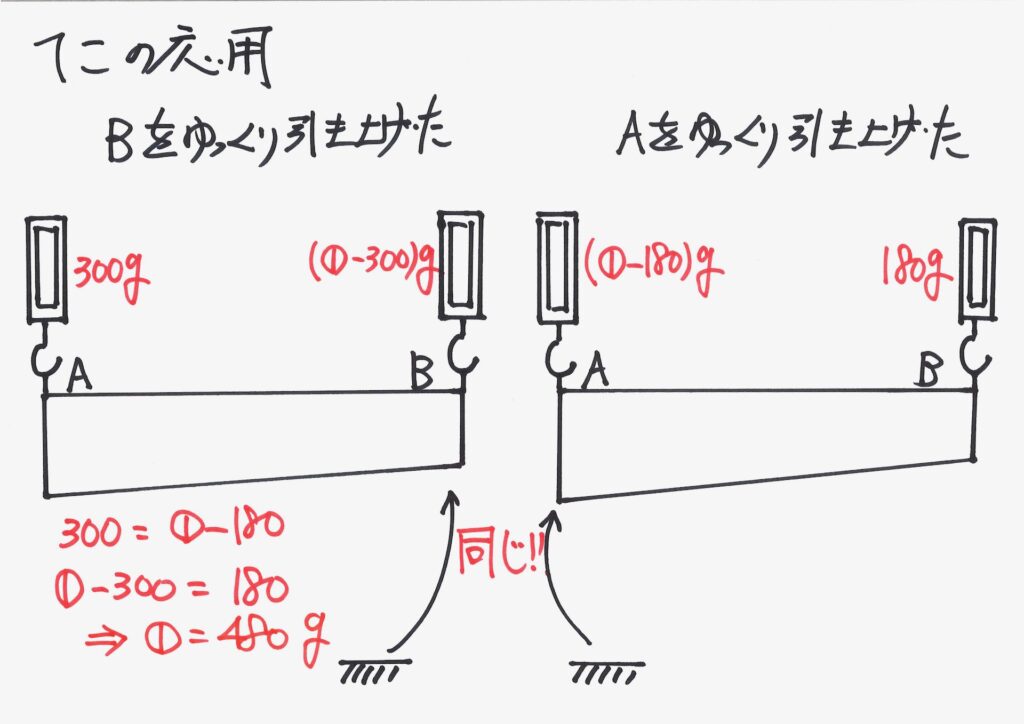
その結果、「同じつり合った状況」となり、棒の重さが分かりました。
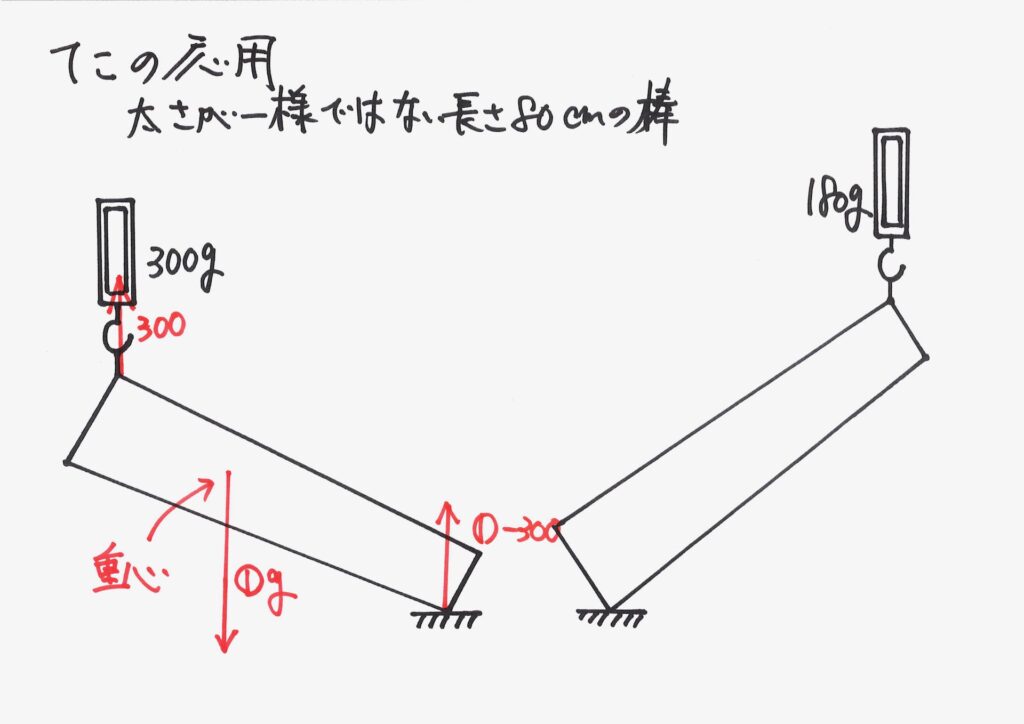
そして、今回は三つ目の考え方である「重心とモーメント」を考えて、棒の重さを考えます。
・複数の（二つの）状況を「重ね合わせる」「足し合わせる」
・ゆっくり、つり合いを保ちながら、反対側などを動かす・引き上げる
・重心と回転する力（モーメント）
男子小学生「重ね合わせる」か
「ゆっくり引き上げる」が分かったなら・・・
男子小学生もう、これ以上
同じ問題を考えなくてもいいよね。
女子小学生私は「重ね合わせる」は、
ピンとこなかったけど・・・
女子小学生「ゆっくり引き上げる」は、
よくイメージ出来たから、これでいいかな・・・
男子小学生僕は「重ね合わせる」で
なんとなく分かったかな？
「問題を沢山解く」と「様々な考え方」が学べるので、学力が上がる傾向があります。
一方で、「同じ問題を異なる視点から考える・別解を考える」姿勢は非常に大事です。
特に、理科・算数では「同じ問題を異なる視点・別解で考える」をやってみましょう。
・「たくさんの問題を解く」より、一つの問題（特に良問）をじっくり
・「同じ問題を異なる視点から考える・別解を考える」姿勢
算数の図形などの別解を考えることも、「異なる視点で考える」ことになり、理解が深まります。
例えば、図形問題で「面積比、辺の比のどちらに着目するか」は、全く異なる視点です。
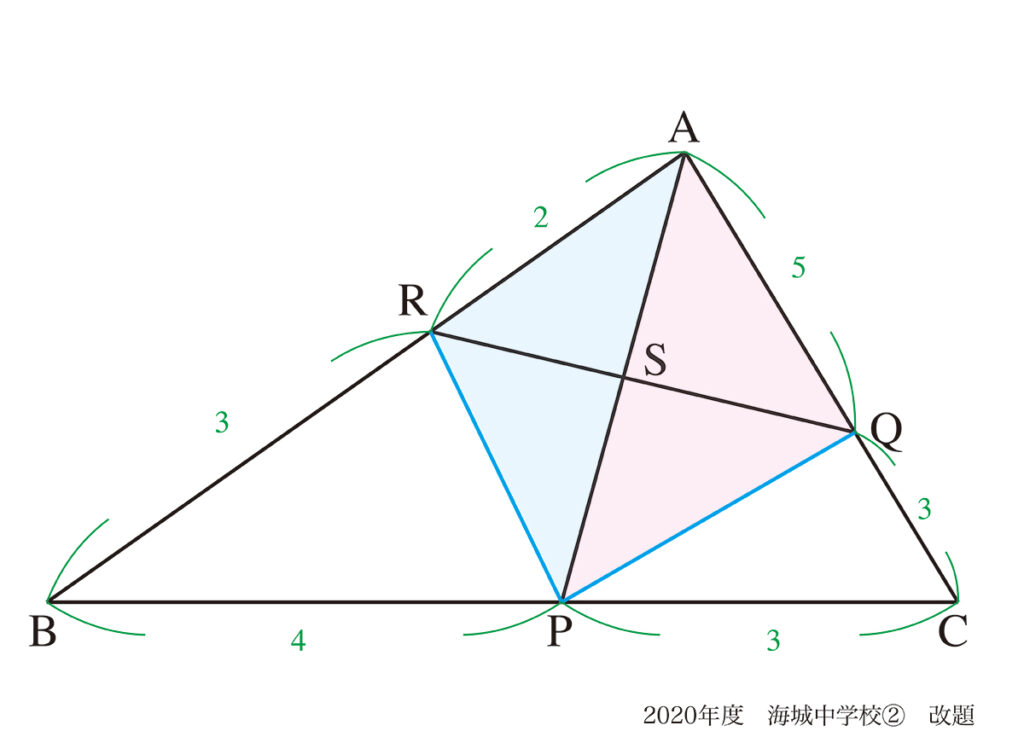
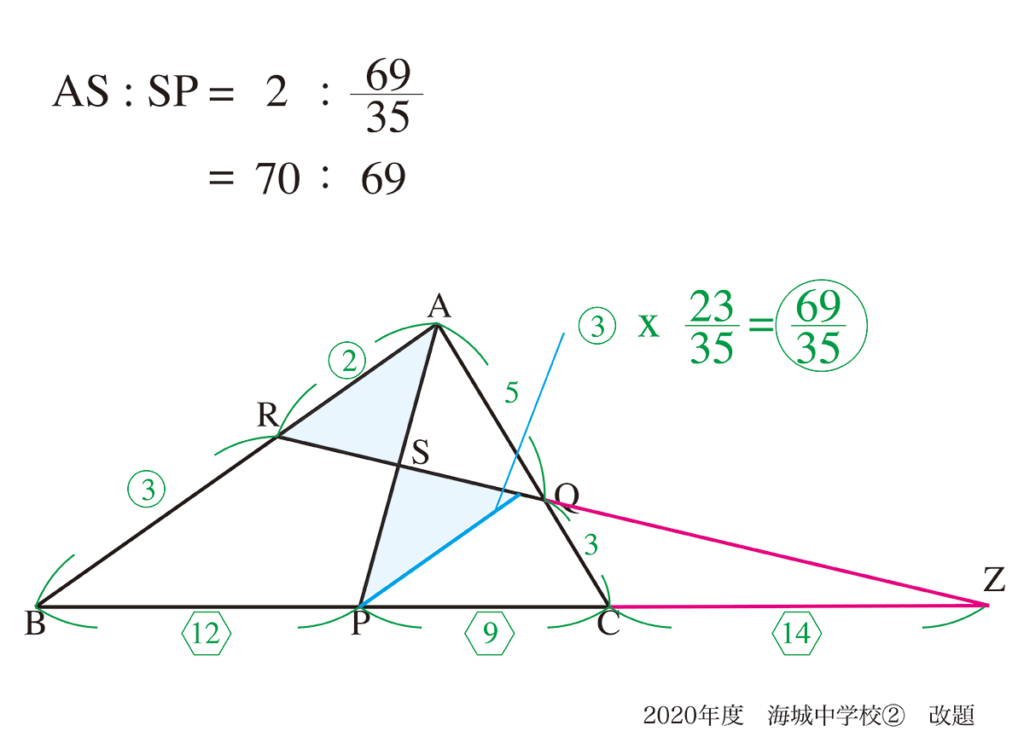
算数の「面積か辺か」は大きな違いであり、理科の上記の三つの考え方も大きな違いがあります。
それらの全く異なる（一部は共通点があります）考え方を、しっかり学ぶこと。
すると、問題・状況に対する視点が複眼的になり見通しがスッと良くなるでしょう。
基本的考えを大事に：複数の未知数
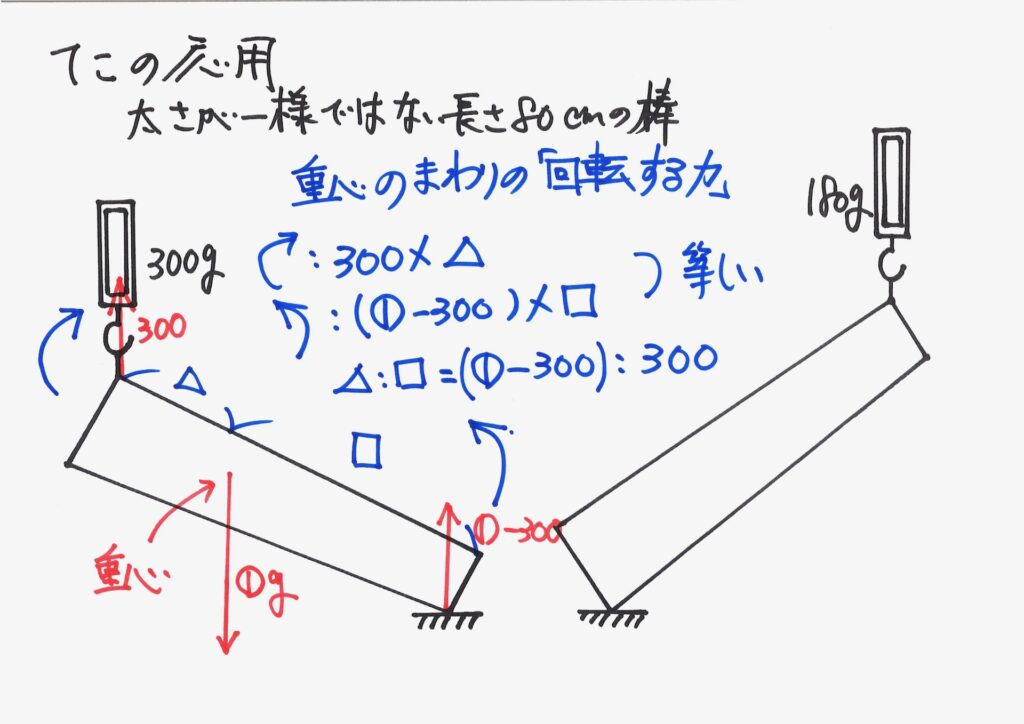
二つの条件のうち、左端の条件から「重心の位置」が分かりました。
男子小学生「重心の位置」が分かったけど、
未知数が三つもあって、ちょっと・・・
女子小学生未知数二つなら分かるけど、
三つになると難しい・・・
ここから先は、中学生・高校生向けの話も含みます。
中学生・高校生にはしっかり理解して頂き、中学受験生は「まあまあ分かる」くらいで良いでしょう。
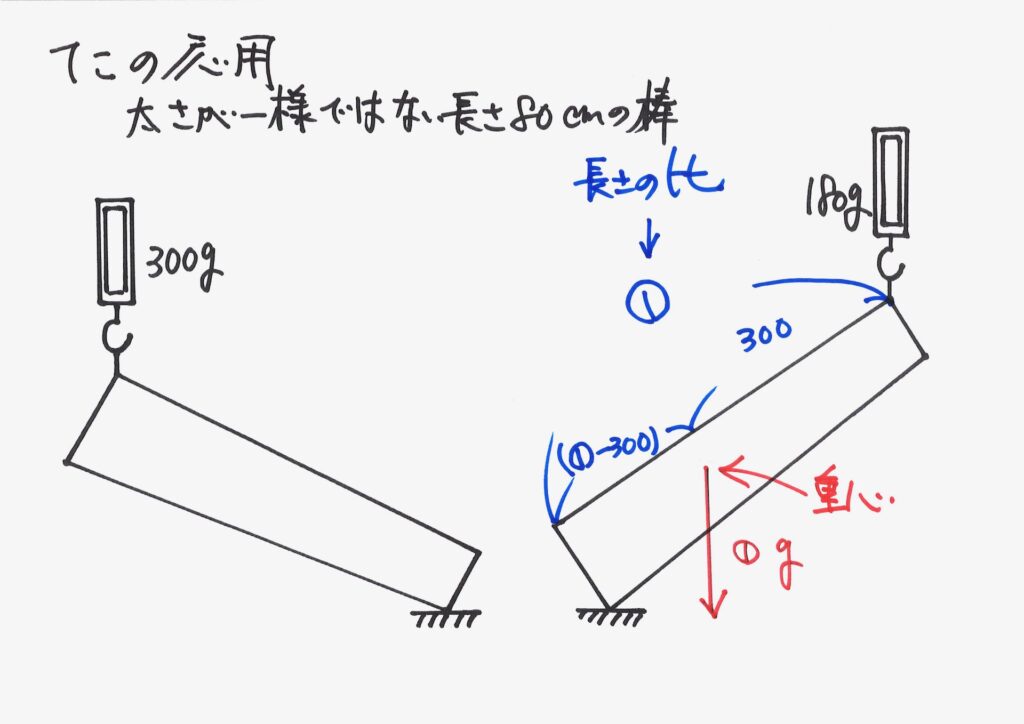
算数・理科は、「わかったこと」をどんどん描くようにしましょう。
女子小学生確かに、
全体の長さは大事ね。
右の状況は「状況は異なる」のですが、「棒の重心の位置は同じ」はずです。
重心の「左の端、右の端からの比」が分かりました。
重心の位置が、棒の左から「①-300 : 300 」の比の位置です。
このように、部分的な長さの比がわかった時は、「全体の長さ」も考えましょう。
そこで、この「①-300 : 300 」の比で重心の位置を考えると、全体の棒の長さは、
(①-300) + 300 =① になります。
そこで、比を足すと「ちょうど①」になります。
男子小学生そう言われたら、そうだけど・・・
なんか不思議だね。
女子小学生でも、
確かにそうだね。
これは、実は「棒の重さを①」とおいたので、全体の長さを比で表すと①となります。
これで、「□と△の未知数」がなくなりました。
男子小学生①だけになったから、
だいぶ簡単になったね！
女子小学生これなら
できそう！
未知数同士のかけ算：式をじっくり観察
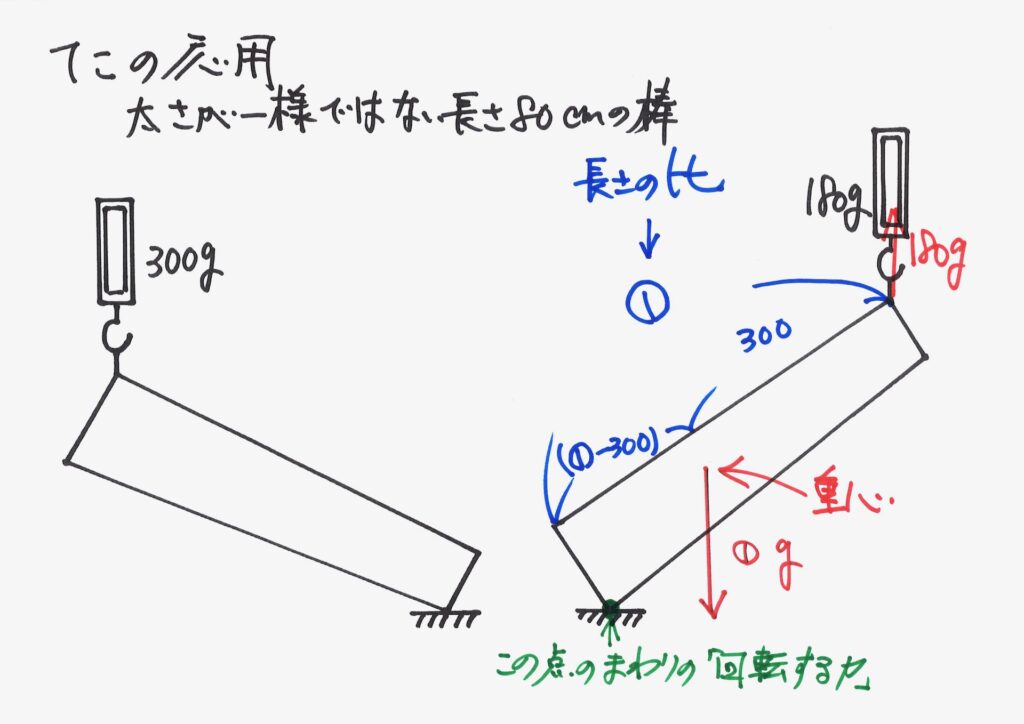
右端を引き上げている時は、左側と同様な状況になります。
棒は「はかりからの力」「重心の重さ」「机からの力」の3つの力を受けます。
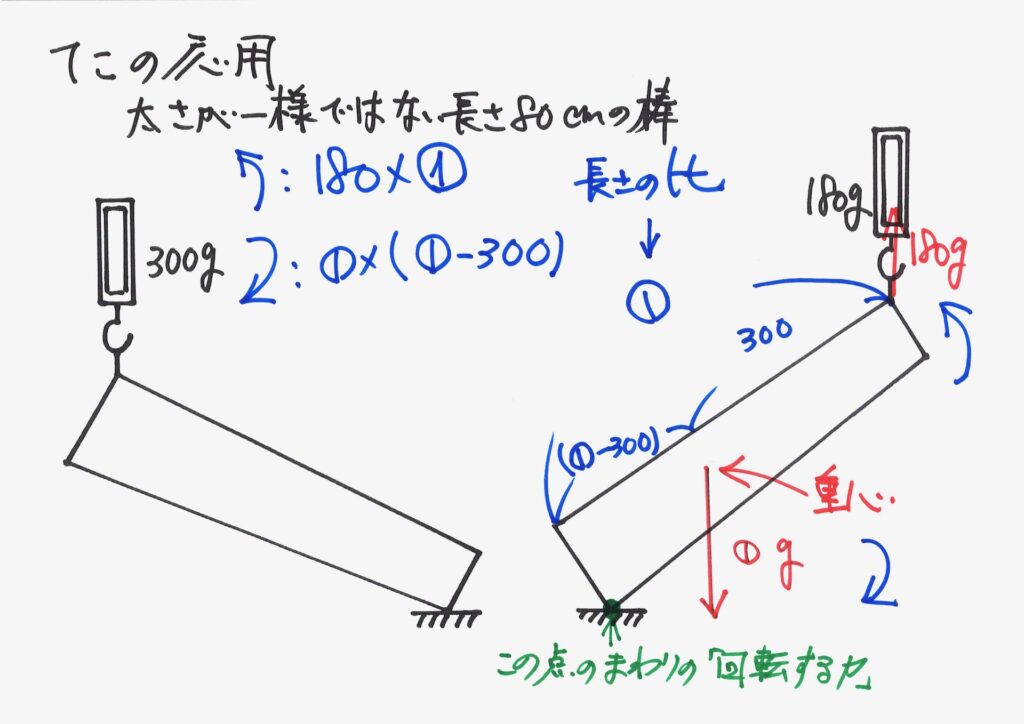
今回は、「棒と机のつながる点（接点）」の周りの「回転する力」を考えましょう。
反時計回り・時計回りの「回転する力」を描いてみます。
描いた上で、「長さx力（重さ）」を考えてみましょう。
男子小学生でも、長さは
分からないよ・・・
女子小学生そう・・・
「長さの比」しか分かってないけど・・・
棒の長さは80cmなので、「比から長さを計算する」のも良いでしょう。
もし全体の長さが分からない（不明）でも、「全体の長さに対する比」を考えてみましょう。
すると「比を、長さの代わりに計算してもOK」と分かります。
「回転する力」が等しいので、式が出来ます。
男子小学生これは、①を二回かける式で、
分からないよ・・・
女子小学生そう・・・
これは、習ってない・・・
この式は「2次式」と表現し、中学の数学で最初の方で習います。
この方程式を解ける方もいるかもしれませんが、「算数的に考える」をやりましょう。
男子小学生でも、
難しそうだよ・・・
何か、「式が簡単になる」方法はないでしょうか。
女子小学生あっ！
右と左で、同じ①をかけてる！
女子小学生「同じ数字をかけて、同じ」だから、
「同じ数字」はなくてもいいはず！
共通する数字は、「割る」などして消しましょう。
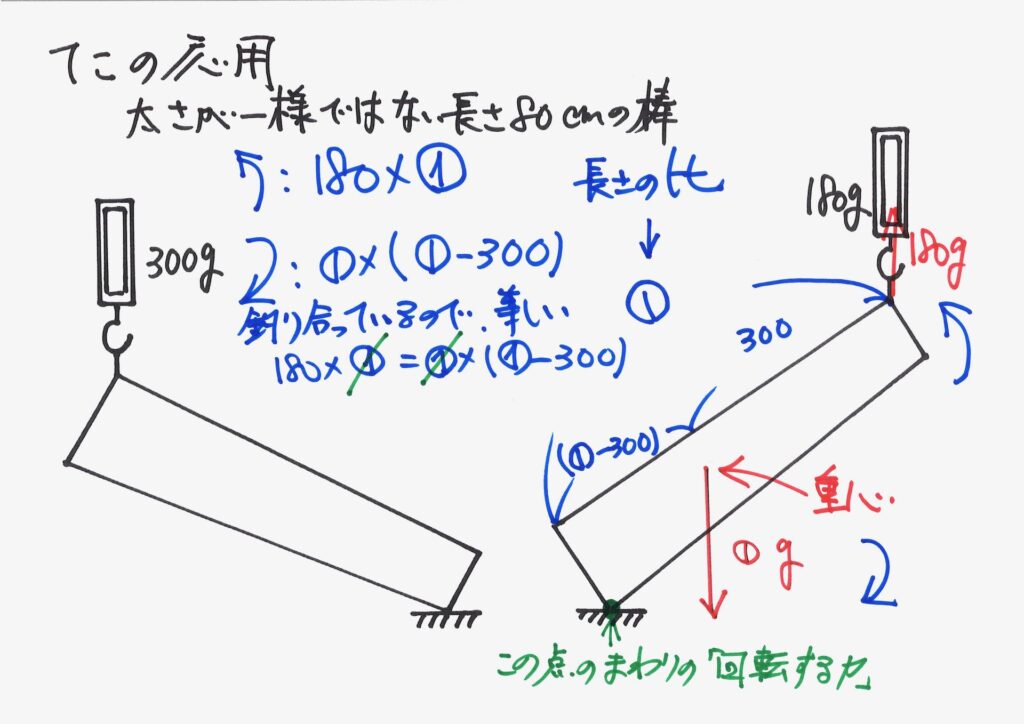
難しそうに見える式も、「式をじっくり観察」すると簡単になることがあります。
これで、簡単な等式になりました。
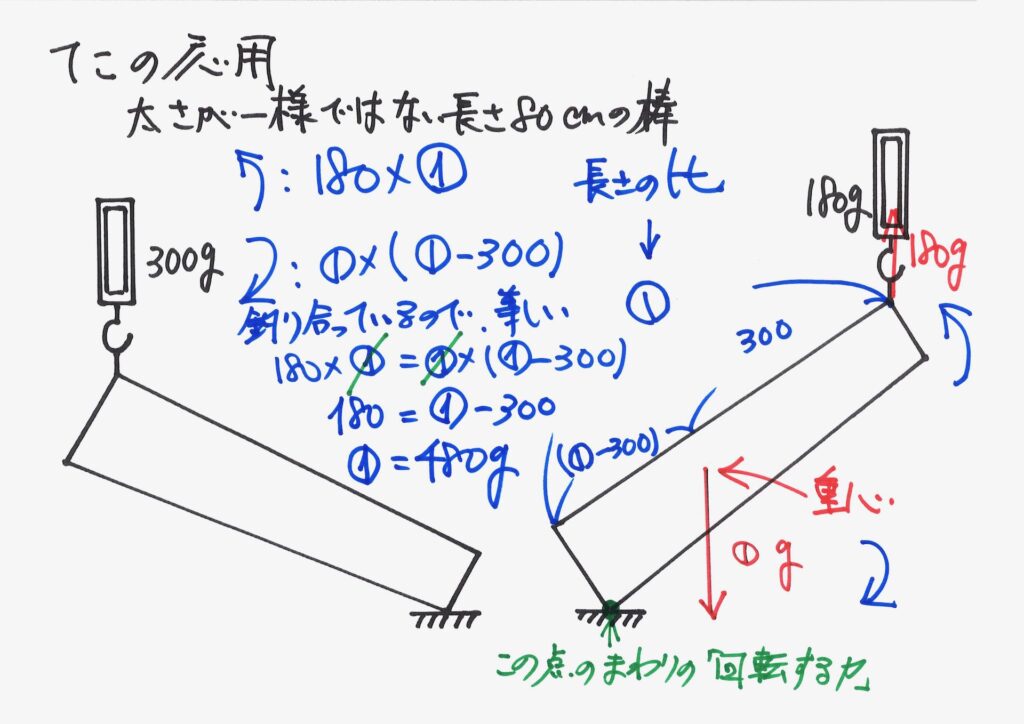
棒の重さが、求まりました。
男子小学生なんか、難しそうだけど、
いろいろな考え方は、楽しいね。
女子小学生違う考え方で、同じ結果になるのは
不思議な感じね。
最後の「重心とモーメント」は、少し難しい考え方かもしれません。
A.複数の（二つの）状況を「重ね合わせる」「足し合わせる」
B.ゆっくり、つり合いを保ちながら、反対側などを動かす・引き上げる
C.重心と回転する力（モーメント）
A,Bは、イメージするのが少し難しいですが、計算は楽でした。
対して、今回考えたCは「未知数が多く、計算が少し大変」でした。
男子小学生Cは、ちょっと難しいけど、
回転する力=モーメントの基本だね。
女子小学生未知数が三つも出てきたり、①x①が登場したり、
ちょっと難しい雰囲気だけど・・・
女子小学生一番考え方が簡単なのは、
Cかも。
今回考えた「A,B,Cの考え方」に対して、それぞれ好みもあると思います。
男子小学生僕はAの考え方が
好きかな・・・
女子小学生私はCが
良いかも・・・
それぞれの子どもの個性によって、「考え方の好み」はあります。
まずは「好きな考え方」をしっかり理解しましょう。
その上で、「他の考え方」も理解するようにするといいでしょう。
理科・算数は、「色々な考え方ができる」のを楽しむ姿勢も大事です。
受験生は、試験の成績などで頭が一杯になりがちですが、様々な考え方をしっかり学びましょう。
その姿勢が応用力を上げて、「難しい問題も解ける」力と姿勢を養うでしょう。
次回は下記リンクです。
