前回は「重心・太さが一様でない棒：モーメント 1〜重心とは何か？・重心と中心・「なぜ？」と思う気持ち・アインシュタインとエジソン・重心は「つり合う」点・たくさんのモノの重心〜」の話でした。
重心とつり合い：日常生活と重心
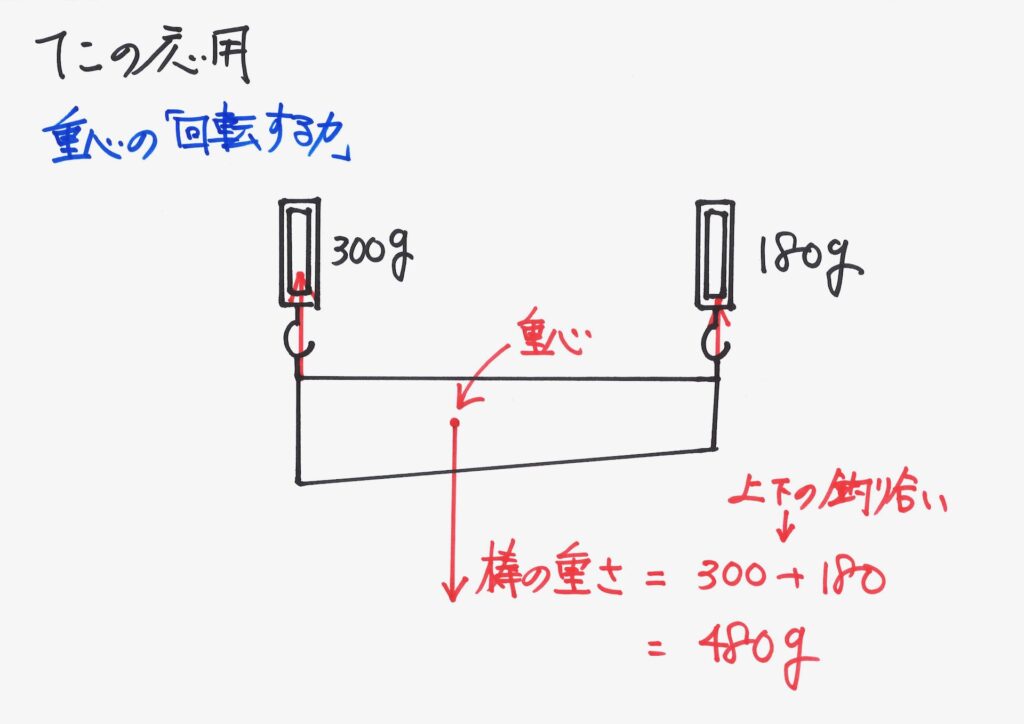
太さが一様ではない棒に対して、重心を考えてみましょう。
「重心」という言葉は、日常生活でも出てくることがあります。
女子小学生そういえば、スキー教室で、
「重心を低くすると滑りやすい」って習った！
確かに、スキーで滑る際は理科の原理的にも「重心が低い方が滑りやすい」です。
男子小学生なぜ、重心が低いと
滑りやすいんだろう？
スキーで滑っている際に「転ぶ」のは、「バランスを崩して転ぶ」ことが多いです。
「バランス」とは、「てこの原理」で考えることが出来ます。
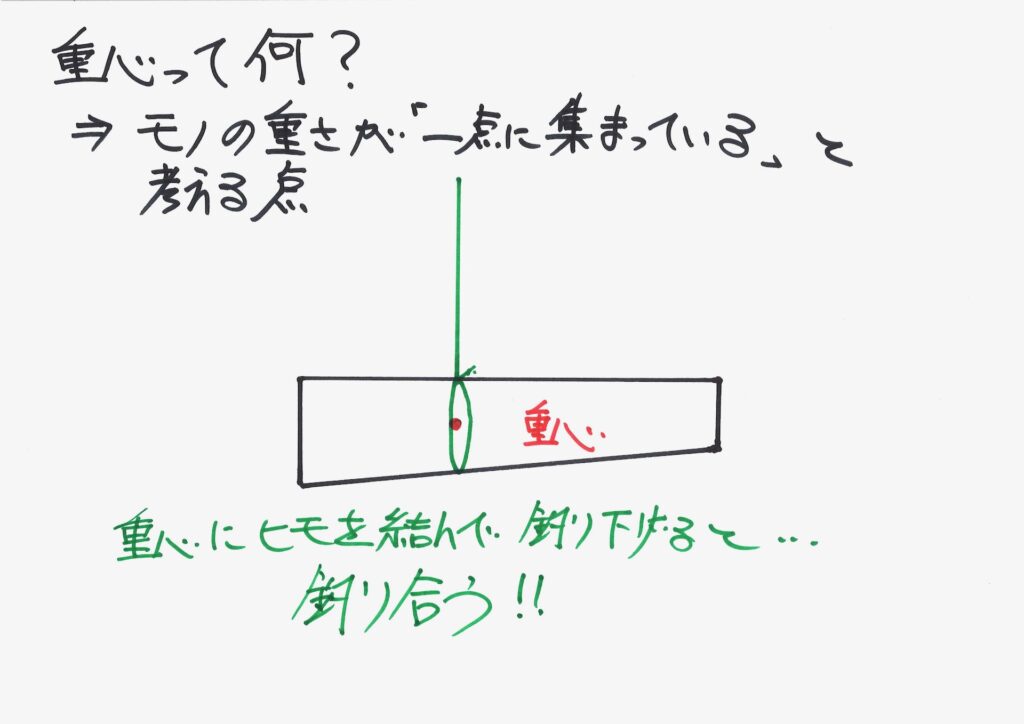
重心とは、「モノの重さが一点に集まっている点」です。
・モノの重さが一点に集まっている点
・重心一点に、モノの重さが全部集まっている
・モノの中心
男子小学生人の体重（重さ）が、
「重心一点に集まっている」とすると・・・
女子小学生地面に対して、人の体重（重さ）が低い方が、
回転する力（モーメント）が小さいね！
女子小学生だから、「重心を下げたほうが滑りやすい」
ということになるね！
「日常生活と密接に関わっていること」が多い理科・物理の学び・勉強。
その中でも、「重心」は比較的「日常生活で耳にする」言葉かもしれません。
この意味でも、「重心」に苦手意識を持たずに、「重心」の意味を楽しく理解しましょう。
重心と回転する力・モーメント
今回は、「ゆっくり引き上げてみた」棒の問題を、重心をもとに考えてみましょう。
「モノの重さが一点に集まっている」と考えられる点と考える「重心」。
重心は、「モノの中心」とも言えます。
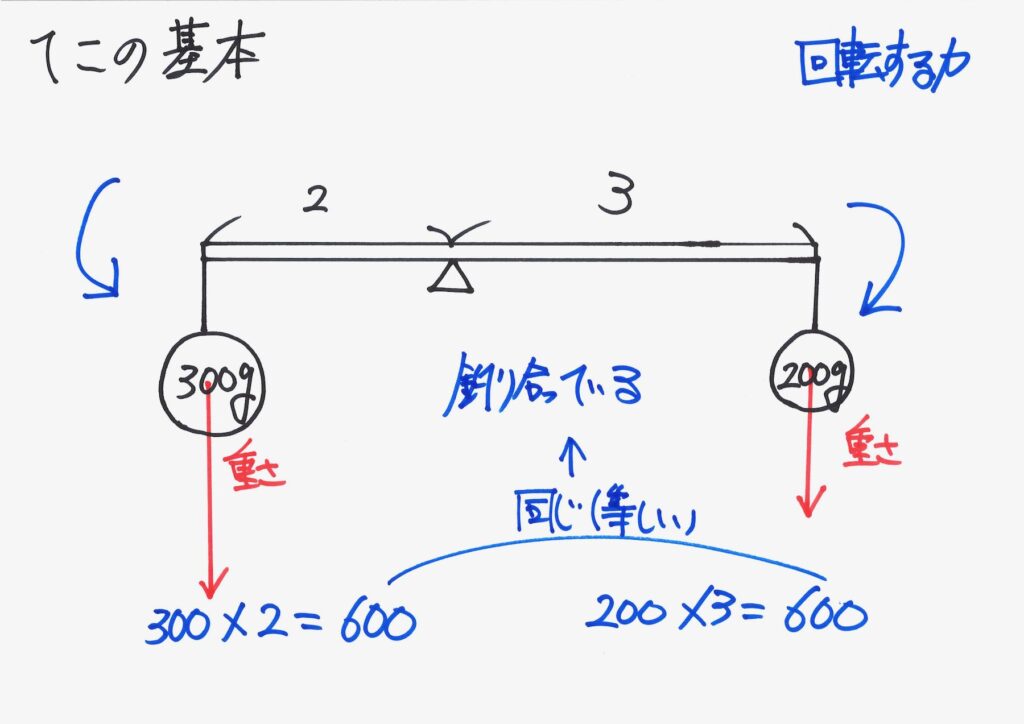
上のような「おもり二つ・てこ（重さなし）」の「三つのモノ」の重心は支点の位置です。
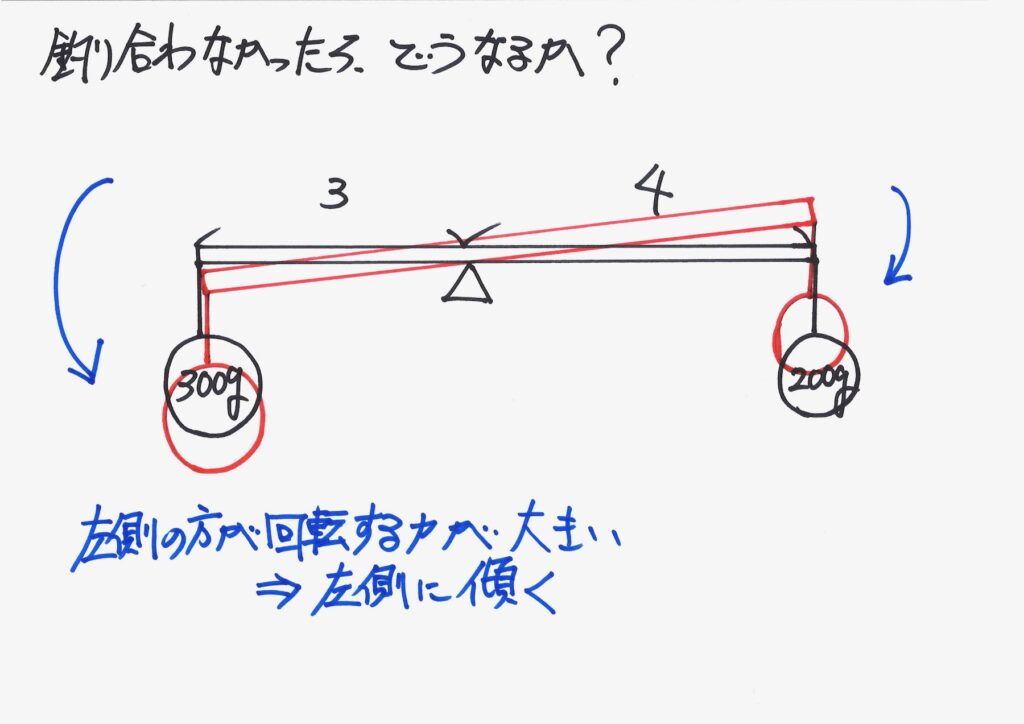
上のように「つり合っていない」状況では、まだ重心の位置は不明です。
この場合、重心の位置は「支点の左側」と「支点の右側」のどちらになるでしょうか。
男子小学生重心は、「モノ（たち）の中心」
だから・・・
男子小学生そこを支えると
「つり合う」はずだね。
女子小学生鉛筆のつり合いと
似ているんじゃない？
男子小学生そうだね。
今、ちょっと左側に傾いているから・・・
男子小学生もう少し、支点を左側に寄せると
つり合いそうだね！
女子小学生そう！
だから、重心は「支点の少し左側」だ！
「重心」を感覚的に理解できると、モノの動きの問題が分かりやすくなるでしょう。
・たくさんのモノを「ひとまとめ」にして考えると、重心がある
・たくさんのモノでも、重心=中心は存在する
「重心」を問う問題は、比較的イメージしやすいので、実験問題等でも出題の可能性があります。
これを機会に、「重心」をしっかり理解しましょう。
太さが一様ではない棒の重心：未知数への姿勢
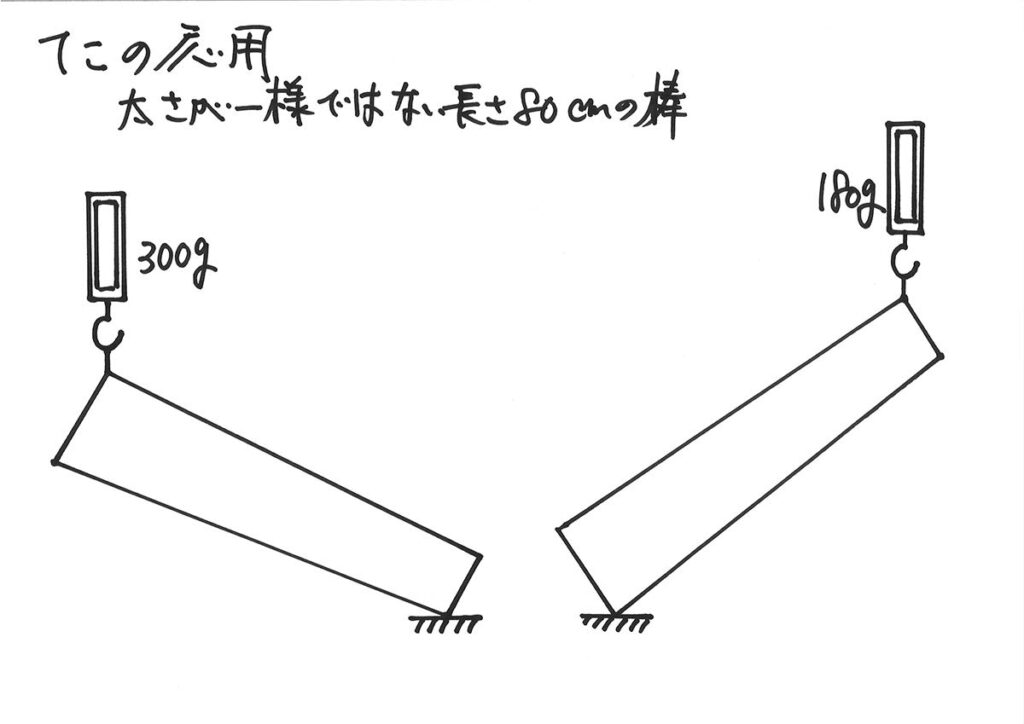
太さなどが「一様な棒」ならば、棒の重心は「中心・中点」となります。
この棒は、「一様ではない」ので、重心の位置が分かりません。
男子小学生左側の方が太いから、
左側の方に少し重さが寄っているね・・・
女子小学生だから、重心は棒の中心・中央よりも
少し左側になるね！
理科・算数では、「具体的な位置」「はっきりとした数字」を求めることが多いです。
一方で、「大体の位置」「大体の数字」をイメージすることも大事です。
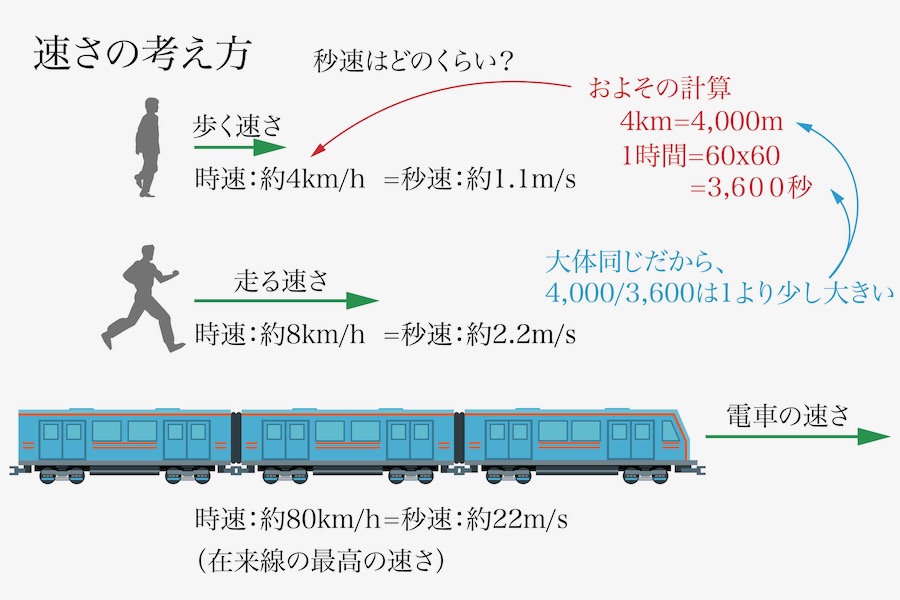
速さも「大体このくらい」というイメージが大事です。
今回は、太さが一様ではない棒の重心を考えて、棒の重さを考えましょう。
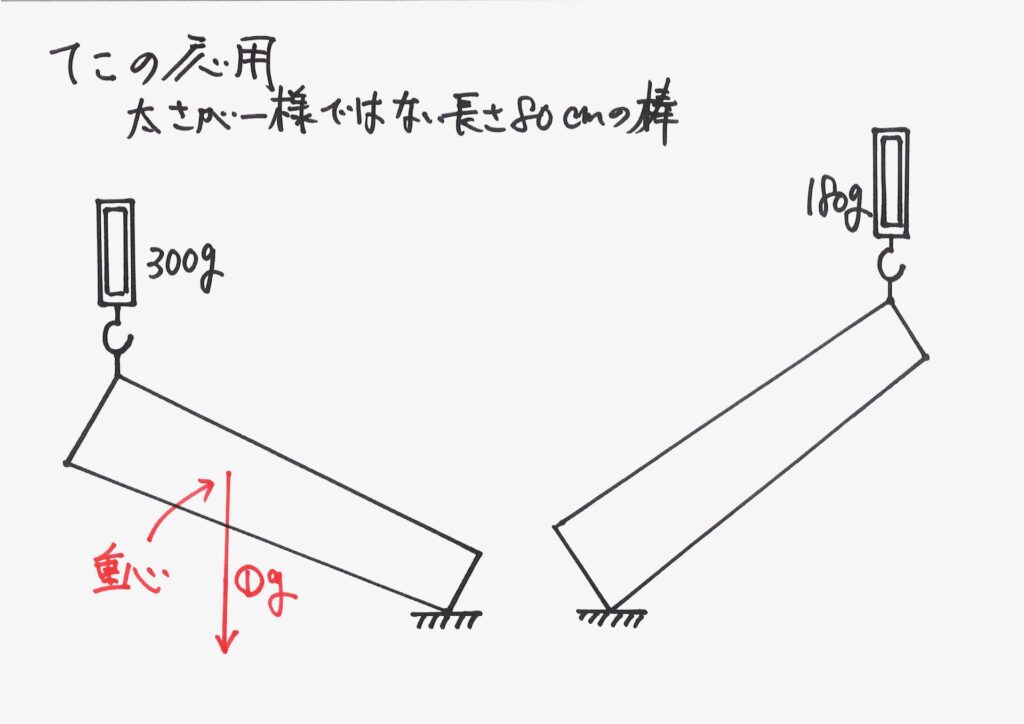
まずは、左側の状態で、棒の重さが不明なので「棒の重さ=①g」と置いて、考えてみましょう。
重心に「全ての棒の重さ=①g」が掛かる、と考えられます。
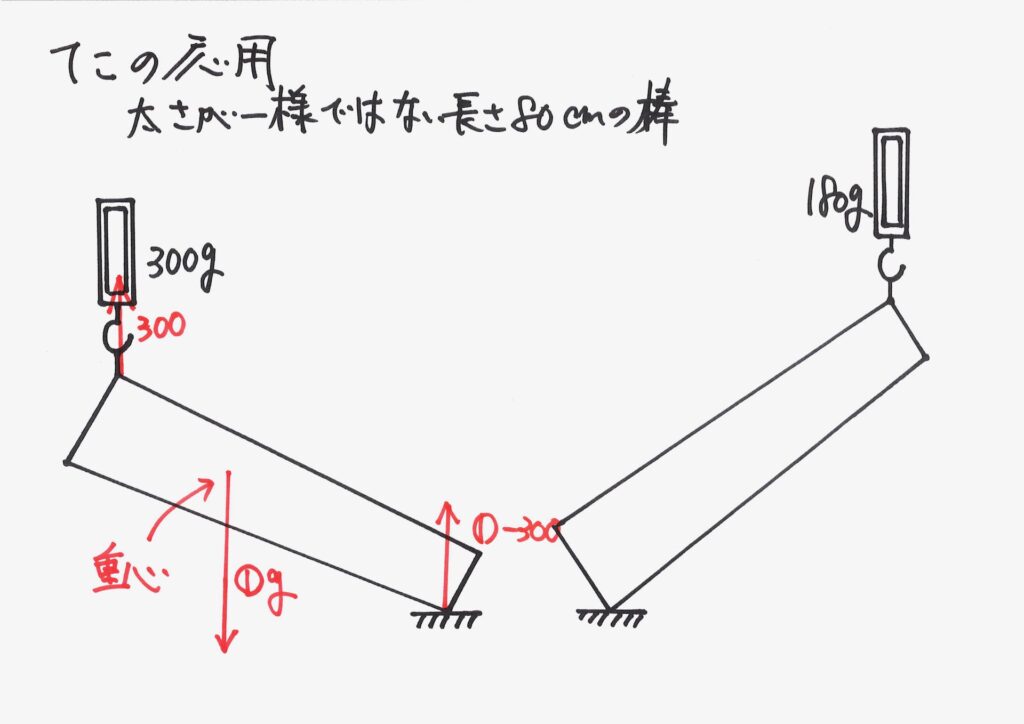
棒にかかる力のつり合いを考えましょう。
棒には「はかりが引き上げる力」「重心にかかる重さ（重力）」がかかります。
そして、棒の重さは残りの「①-300」gが、机にかかり、机から同じ力を受けてつり合います。
男子小学生これは、分かるけど、
ここから進むのかな？
重心の位置が分かりませんが、「回転する力」を考えましょう。
「釣り合っている点」であれば、どこで考えても、「モーメント（回転する力）もつり合う」です。
「回転する力」は、「重さ（力）x長さ」です。
そこで、「回転する力の釣り合い」から、「長さの比」が分かります。
「棒が受けている力」から「回転する力（モーメント）」を考えてみましょう。
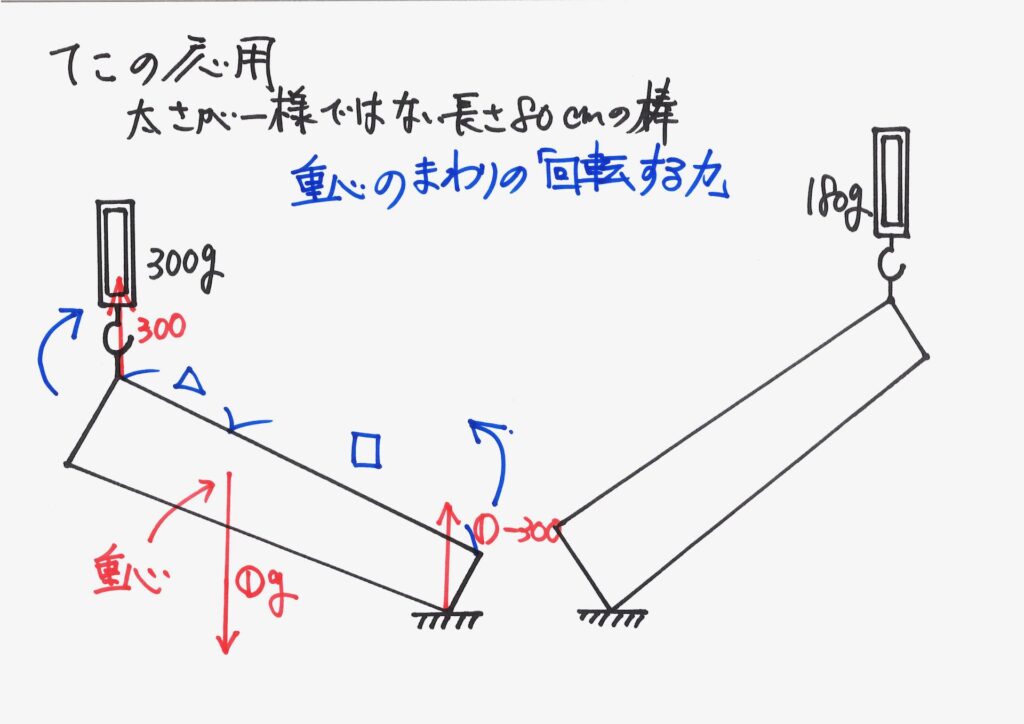
「重心の位置」を知るために、（左の端から重心） : （重心から右の端）の比を置いて考えましょう。
ここでは、「（左の端から重心） : （重心から右の端）=△ : □」と置きました。
未知数は、自分の好きなようにおいてみましょう。
男子小学生三つも「分からない数」が
あるよ・・・
男子小学生ちょっと
難しいよ・・・
この辺りからは、中学生・高校生向けの話になります。
中学受験生の方は、「なんとなく」わかれば十分です。
沢山、分からない量（未知数）が出てきて、難しく見えますが、基本的考え方で進めましょう。
女子小学生「回転する力」は、「力がかかっている点の回り」を
考えると簡単なはず！
男子小学生長さの比は、
「力の逆比」だね！
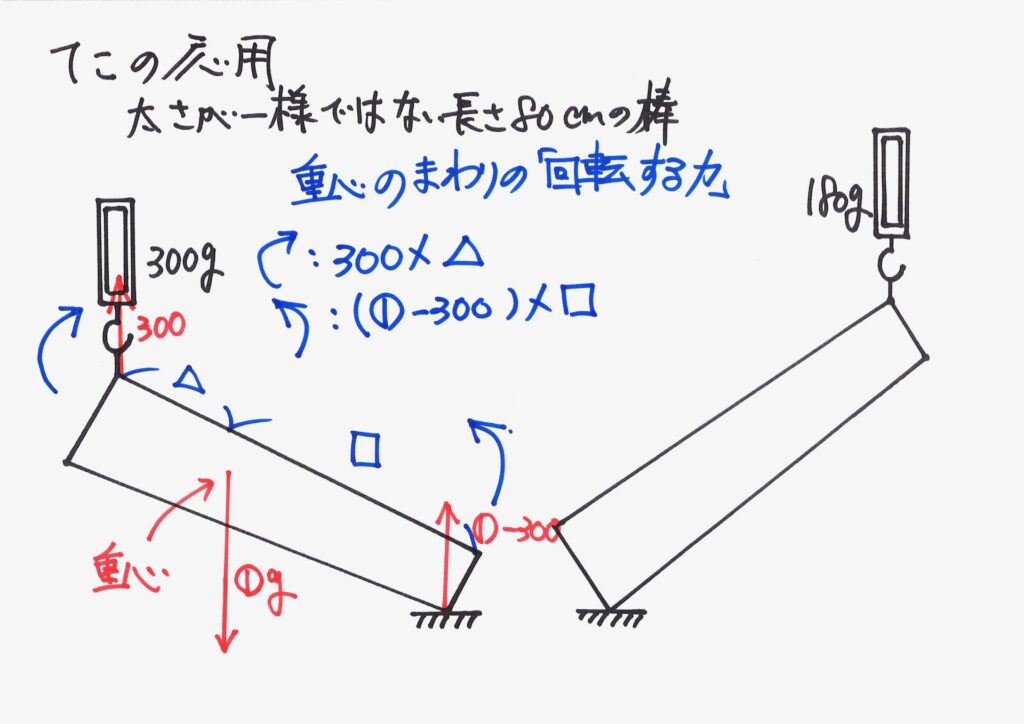
重心を中心とする「回転する力（モーメント）」を考えると、比較的簡単になります。
「重心のまわり」の「回転する力」は、釣り合っているので、考えてみましょう。
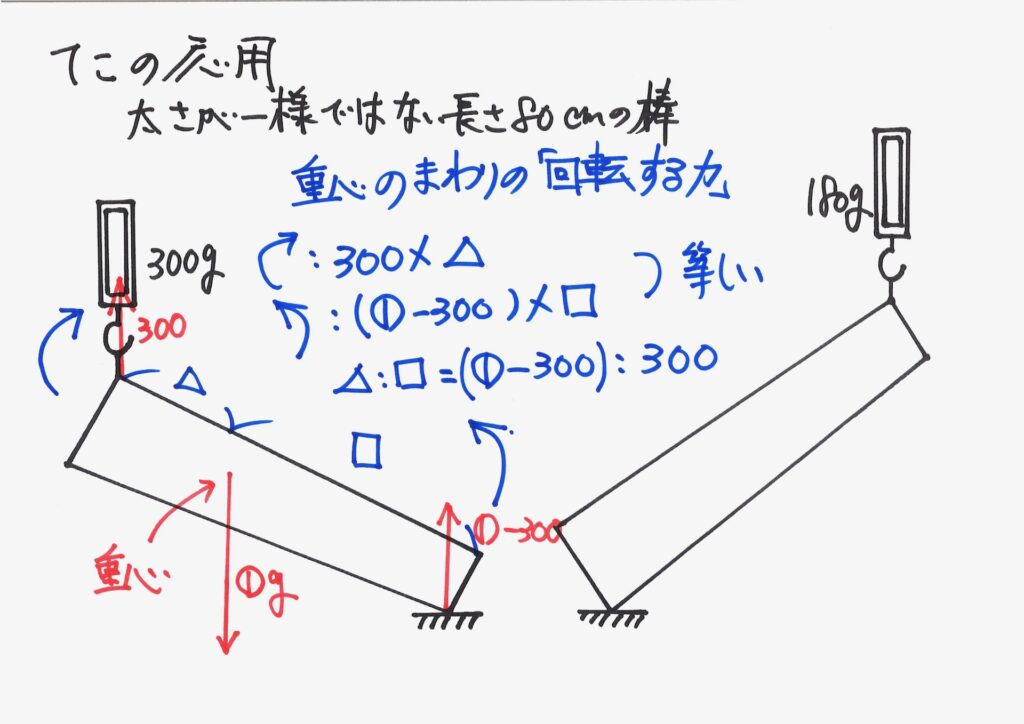
時計回りの「回転する力」と、反時計回りの「回転する力」が等しいです。
これで、長さの比が分かりました。
男子小学生今回も、
長さの比=「力の逆比」になったね。
女子小学生基本的なことを理解していると、
分かりやすい！
男子小学生「こうかな」と思った通りになると、
嬉しいね！
「逆比」などの力学的な事を丸暗記ではなく、「理解して、自然と覚える」と応用力も上がります。
これで、左側の条件から「重心の位置」が分かりました。
この「重心の位置」をもとに、右側の条件を考えてみましょう。
今回は未知数が三つも登場して、少し難しくなりました。
「未知数が二つ」までは、中学受験生も「面積算」等でやったことがある方がいらっしゃるでしょう。
男子小学生うん。
未知数が二つまでは、出来るけどさ・・・
男子小学生三つも未知数があったら、
分からなくなるよ・・・
分からない対象に対して「未知数を設置する」姿勢は、少し数学的・物理的発想です。
「分からない対象を未知数で設置」した時に、大事な姿勢があります。
それは、「全て分かろう」とせずに「少しでも分かることがあれば良い」という姿勢です。
「全て分かろう」とすると、分からない対象・未知数が増えた時、大変です。
女子小学生出来るだけ分かれば良い、
くらいな感じかな？
・「全て分かろう」とせずに「少しでも分かることがあれば良い」という姿勢
・未知数の数と同じ数の「独立の式・関係式」があれば、未知数は全て分かる
算数実践の問題６で、未知数が三つ登場しました。
そして、分かった関係式に対して未知数を計算してみました。
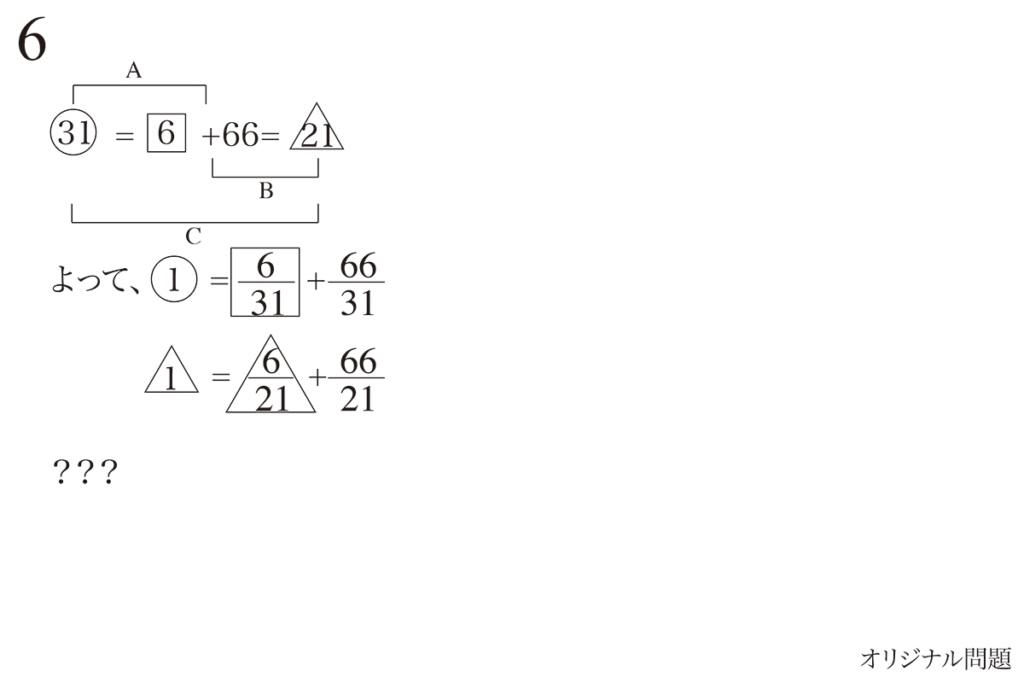
ところが、計算しても途中で進まなくなりました。
この時は、「未知数が整数である」性質を考えることで解くことができました。（上記リンク）
「三つの未知数に対して、独立した等式が二つ」だったので、答えに辿りつかなかったです。
男子小学生「独立した」等式って
何？
「独立した」等式は中学以降の数学で学びますが、「他の関係式から導けない式」です。
女子小学生ちょっと
分かりづらいけど・・・
先ほどの整数問題の例で、「AとBから、Cが分かる」です。
同様に、「AとCから、 Bが分かる」、「BとCから、Aが分かる」です。
比較的簡単な分数の計算なので、ぜひ、計算してみてください。
この整数問題では「途中から整数の性質」を利用しました。
理科では「何かの性質」を考慮するか、「分かる範囲で良い」姿勢で考えるようにしましょう。
あまり難しく考えすぎないで、「どこまで分かるかな」と好奇心を持ってみると良いでしょう。
次回は下記リンクです。
