重心・太さが一様でない棒：モーメント 1〜重心とは何か？・重心と中心・「なぜ？」と思う気持ち・アインシュタインとエジソン・重心は「つり合う」点・たくさんのモノの重心〜｜中学受験・高校受験・大学受験・理科

前回は「てこ・太さが一様でない棒：動いてつり合う状況のイメージ 3〜動きを極めてゆっくりする止めるイメージ・理想的状況・二つの状況を比較・考え方を比較・似ている点と異なる点〜」の話でした。

太さが一様でない棒がつり合うイメージ：重心とは何か？重心と中心

「太さが一様である棒」を考えることが多いのに、「太さが一様ではない棒」を考えました。

この「太さが一様ではない棒」が突然登場するので、

「難しい」と感じる方も多い分野です。

特殊なように感じられる「太さが一様ではない棒」。

実は、身の回りの棒は「太さが一様ではない棒」が沢山あり、「太さが一様である棒」が特殊です。

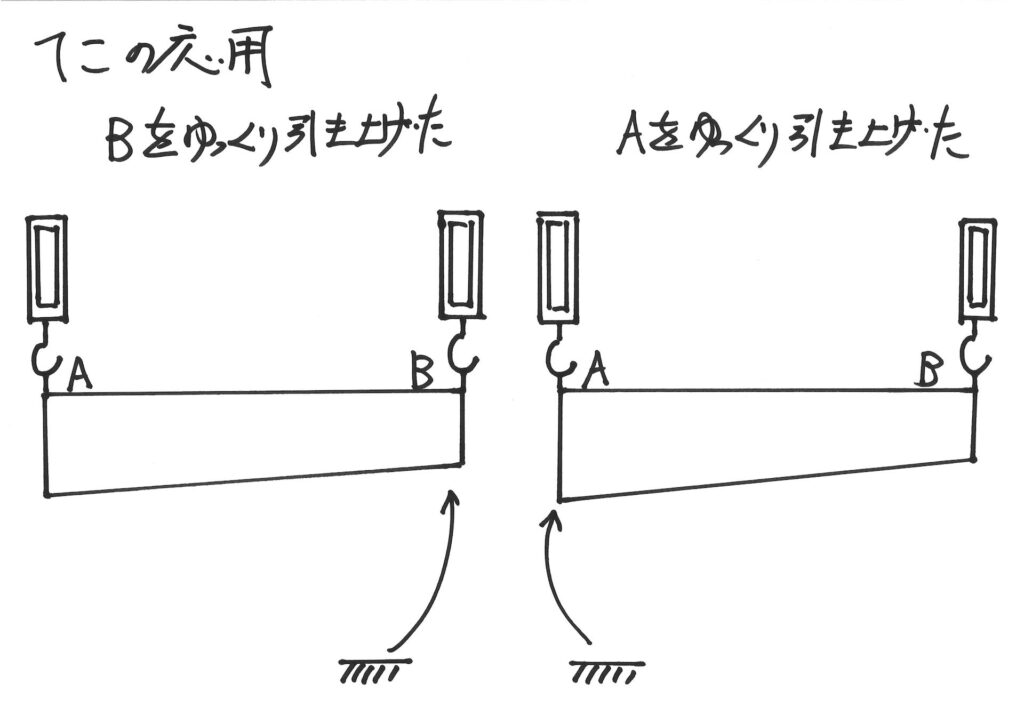
この「太さが一様ではない棒」に対して、一番多い問題は「左端・右端を別々に引き上げる」です。

「引き上げた」という状況に対して、反対側の端を「ゆっくり、極めてゆっくり」引き上げました。

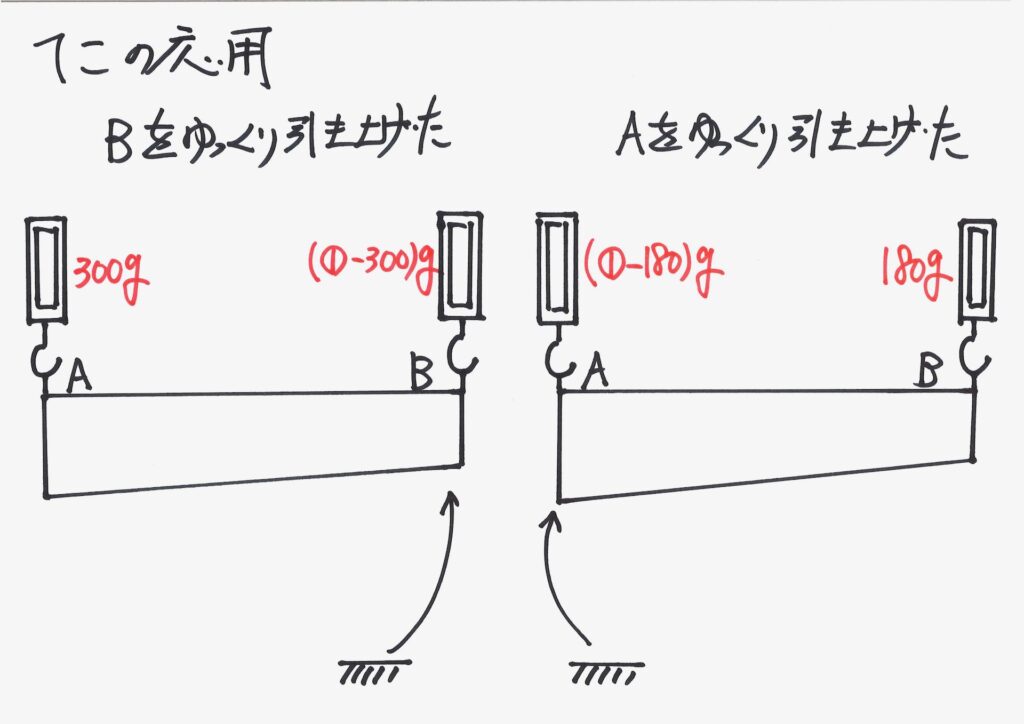
この時、「ゆっくり、極めてゆっくり」引き上げるイメージは、「常につり合っている」イメージです。

そのため、「出来るだけ揺らさずに、ゆっくりゆっくりと引き上げる」のです。

実際に「揺らさずに、ゆっくり引き上げる」のは「簡単そうで簡単ではない」です。

そこで、頭の中でイメージして、「理想的状況」を思い描きましょう。

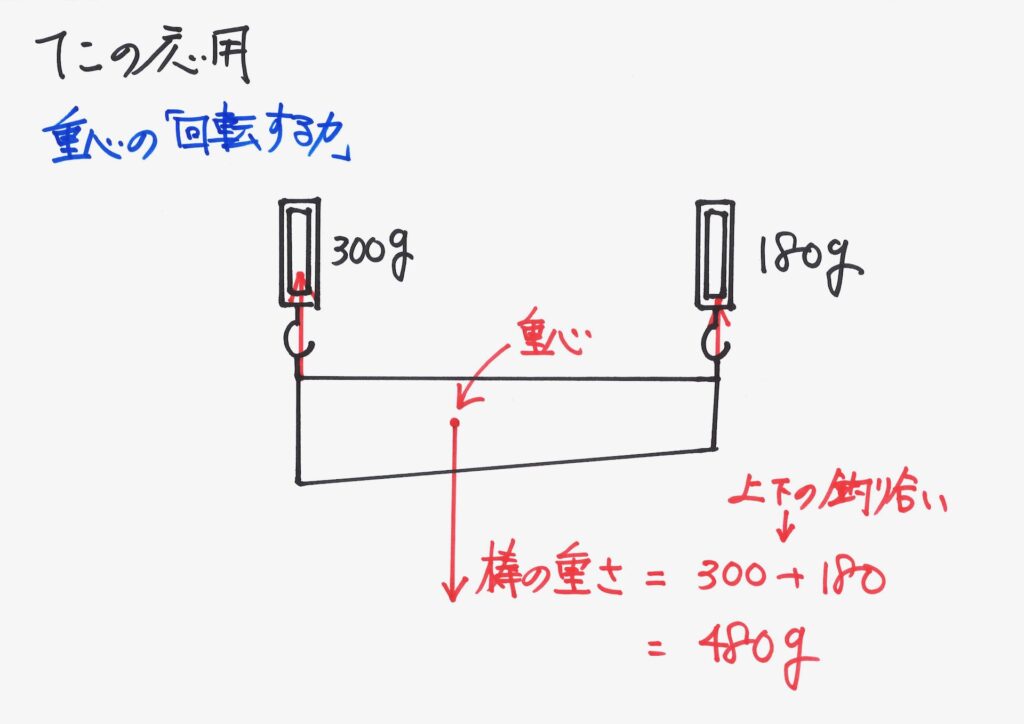
今回は、重心の話です。

重心は小学校で習うかどうかは、学校のカリキュラム・塾の方針にもよると思います。

算数にも関わるので、あまり難しく考えずに、「重心」を考えましょう。

てこを考えたときに、重心の話をしました。

重心とは「モノの重さが一点に集まっている」と考えられる点です。

重さのある棒は「全ての点（場所）に重さがある」です。

「重心一点に、重さが全部集まっている」と考えることが出来ます。

いわば「モノの中心」と考えましょう。

これが、重心の非常に大事な性質です。

確かに「不思議な感じ」がします。

こういう時に「なぜ？」と思う気持ちは大事です。

「なぜ？」と思う気持ち：アインシュタインとエジソン

アインシュタインとエジソンには、子どもの頃に「共通した姿勢」を持っていました。

アインシュタインもエジソンも小さな頃、未就学児・小学生くらいの頃に、

「なぜ？」を考えました。

少し大人しめだったアインシュタイン少年は、

一人で考え続けて、ちょっと「内向き」でした。

アインシュタイン少年より、少し「外向き」だったエジソン少年は、

「なぜ？」先生や周囲の方に問い続け、煙たがられてしまい、小学校退学に至りました。

後になって考えれば、むしろ「小学校退学が良かった」エジソン。

本人や親にとってみれば「退学に追い込まれた」ようなもので、内心は相当ショックだったでしょう。

この二人以外にも、様々な偉業を挙げている方の最も大事なことは「なぜ？」と思う好奇心です。

この「好奇心」こそが、「大発見の原動力」なのでしょう。

この意味において、勉強しているとき、「なぜ？」と思う気持ちを持つと、

「頭が良くない」と誤解しがちですが、そういうことはありません。

「なぜ？」と思わずに、「なんとなく分かる」と「飲み込みが早い優秀な子」と評価されがちです。

中学受験〜大学受験においても、

「鉄則」などを塾で教わり、その「鉄則通り」に問題が解けると成績が上がります。

「解ける」は実は、「単に言われたことを疑問に思わずに分かっている」だけかもしれません。

「なぜ？」と思う余裕は、ないかもしれません。

「効率良く成績・点数を上げる」ことが必要な受験生。

時には「なぜ？」と思う気持ちを楽しみながら、「効率も良く」やってみましょう。

重心は「つり合う」点：たくさんのモノの重心

使用前の鉛筆ならば、「鉛筆の中央・中心」に指をかけると、つり合います。

ところが、使用中の鉛筆は「鉛筆の中央・中心」に指をかけると、

「同じ鉛筆」ですが、物理的に考えると、使用前と使用中の鉛筆は「異なる」のです。

同じ鉛筆は、削った時点・瞬間で物理的には「違う鉛筆」に変身します。

モノには、基本的に「すべての部分」に重さがあります。

重心は「あるモノ」に対して、「すべての重さが一点に集まっている」と考える点です。

棒を二つに切ったら、それぞれの棒に重さがあり、それぞれの棒に「新たな重心」が出来ます。

ここで「なぜ？と思う気持ち」「少し不思議な気持ち」があったら、良いことです。

理科や算数は、「なぜ？」と根源的に考える姿勢が大事です。

一方で、「一気に理解しようとしない」姿勢も大事です。

少し曖昧な状態でも、先に進んだら、

「一気に分かる」こともあるので、進んでゆきましょう。

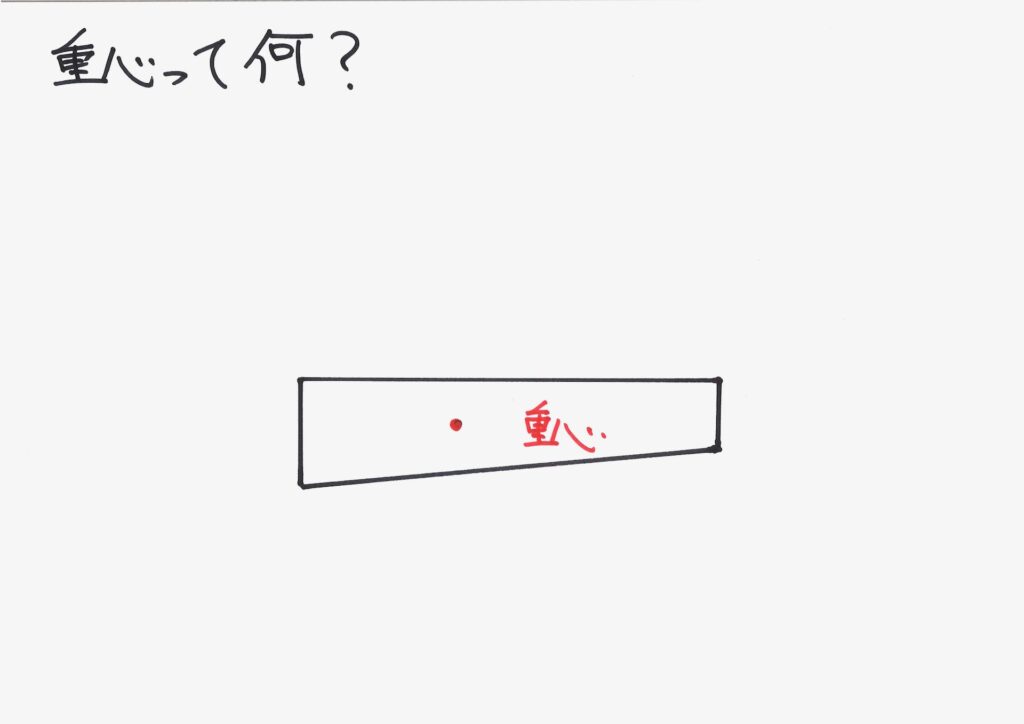
今回考えた「太さが変わる=一様ではない」棒の重心を考えましょう。

重心は「モノの重さがそこに集まっている」点です。

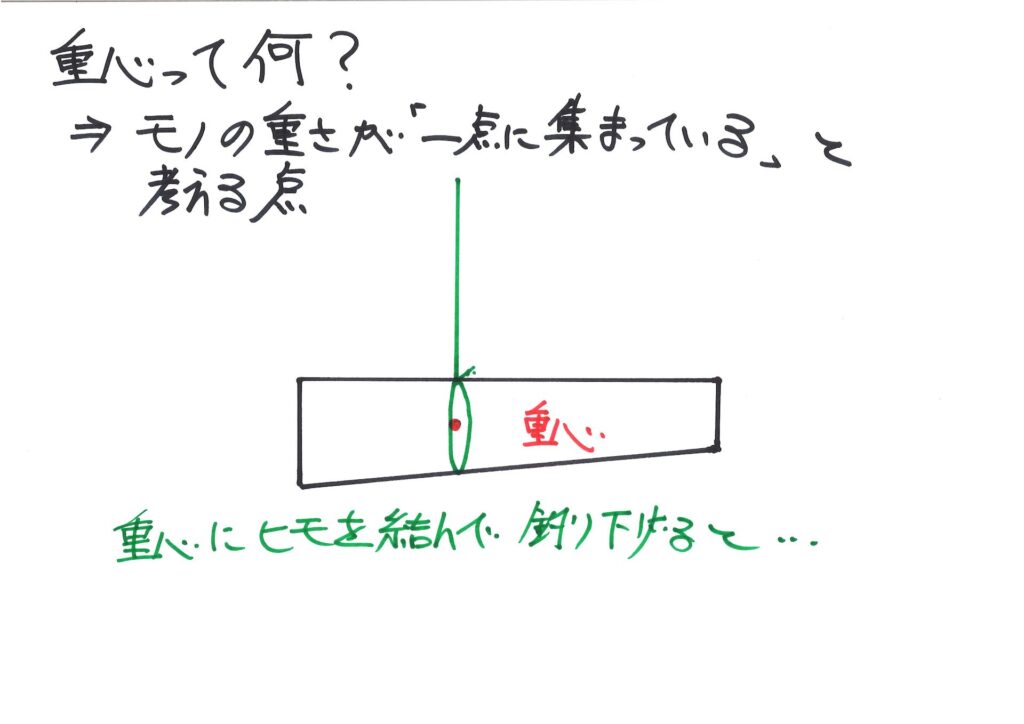
「重さが一点に集まっている」ので、ちょうどその点にヒモを結んで吊り下げてみましょう。

すると、どうなるでしょうか？

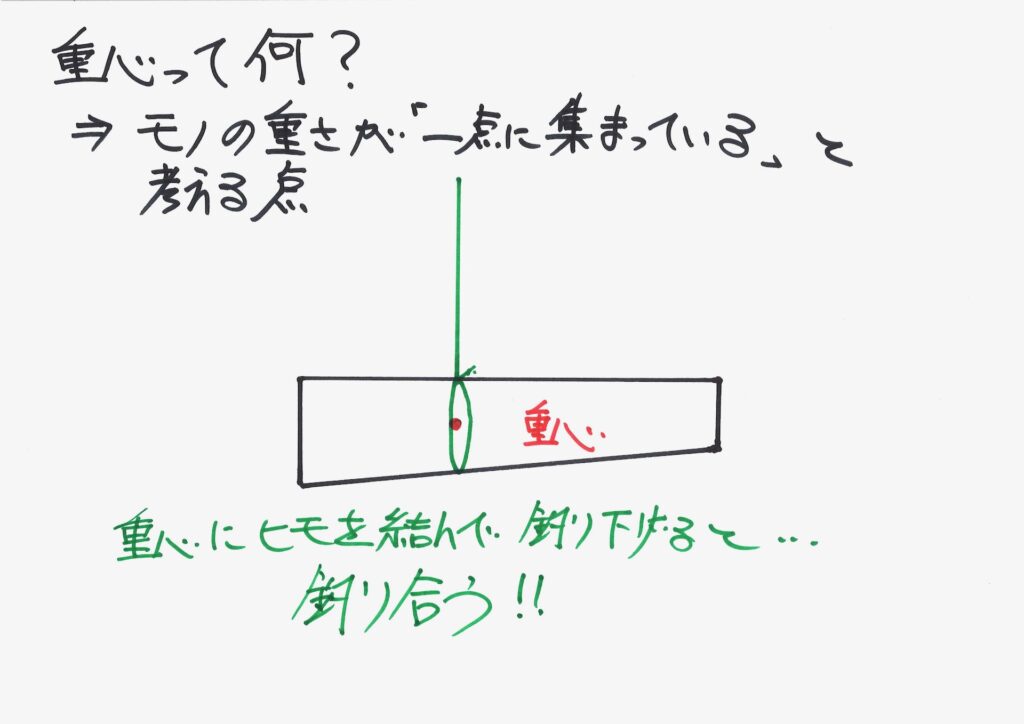
「一点に集まった重さ」をヒモで引っ張れば、釣り合うはずです。

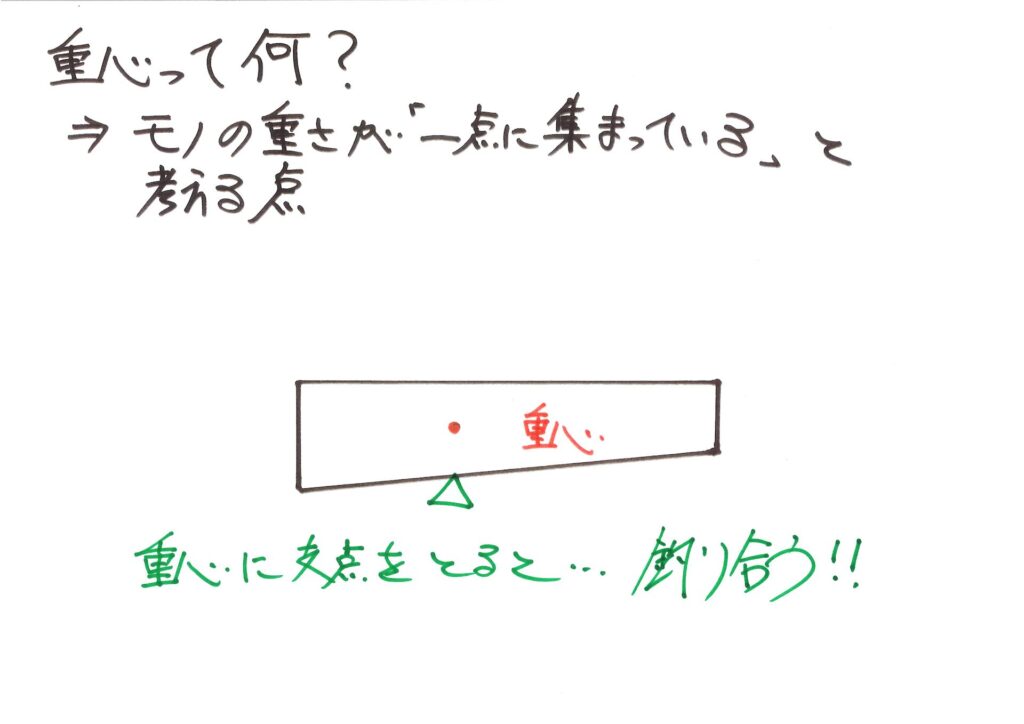
あるいは、棒の重心の真下に支点を取ると、つり合うはずです。

この重心に「全ての重さが集まっている」のですから、「そこを支えればつり合う」はずです。

「棒の下側が斜め」であることは、ここでは気にしないようにしましょう。

「棒のバランス」を考えます。

「重心に重さが集まっている」ので、その点以外には「重さがない」と考えることが出来ます。

そこで、棒の重心に支点を取ると「つり合う」のです。

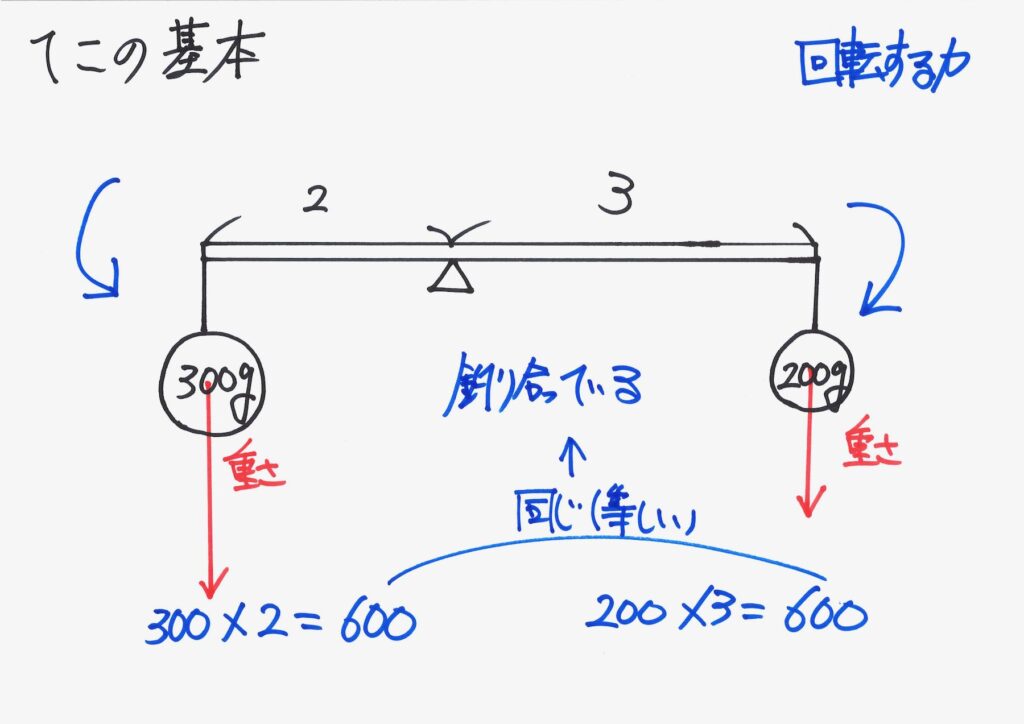
てこがつり合っている状況は、「てこ（重さなし）・おもり二つの合計三つの重心=支点の位置」です。

てこは「重さがない」前提なので、厳密には上のつり合いは「おもり二つの重心=支点の位置」となります。

実は、二つよりも多い三つでも四つでも、いくつモノがあっても「重心は考えられる」のです。

重心は「つり合う点」あるいは「モノの中心点」というイメージを持っていれば良いでしょう。

次回は下記リンクです。