前回は「てこ・太さが一様でない棒：動いてつり合う状況のイメージ 2〜動きをイメージ・つり合うこと・バネ・てこ・かっ車・モノの動き・鉛筆で実験・ゆっくり動かすイメージ〜」の話でした。
動きを極めてゆっくりする・止めるイメージ：理想的状況
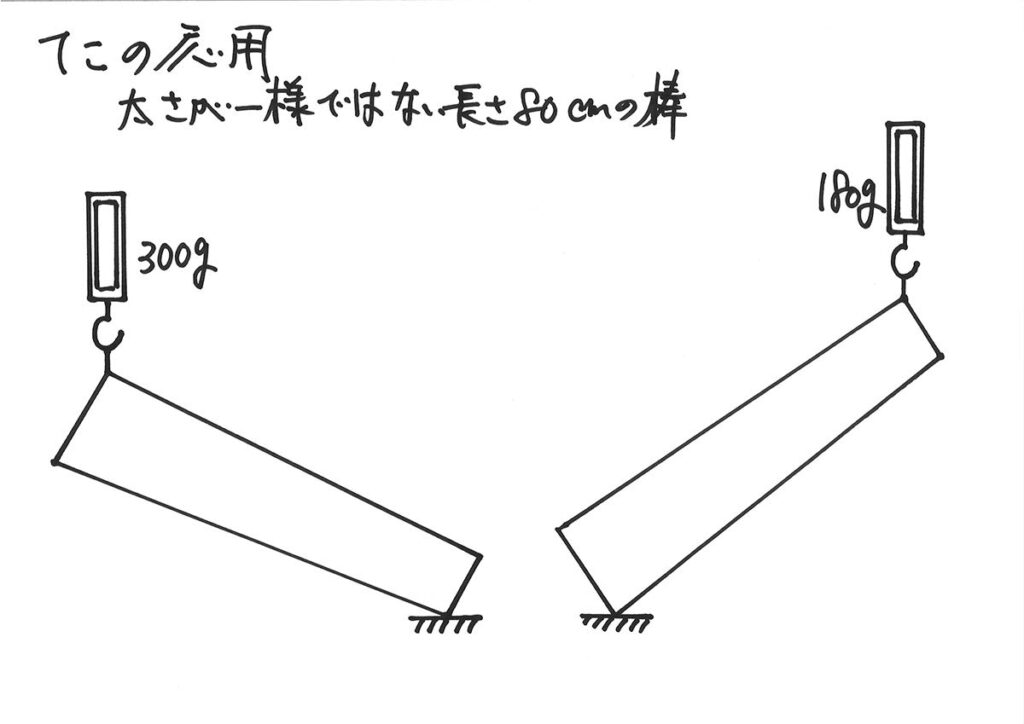
太さが一様ではない棒の両端を別々に引き上げている状況に対して、別の端を持ち上げました。
その時、「ゆっくり、極めてゆっくり引き上げる」ことが、ポイントでした。
この理由は「ゆっくり、極めてゆっくり引き上げる」=「常につり合っている」状況です。
実際、「常につり合っている状況」となるように「ゆっくり引き上げる」のは、難しいです。
「ただ引き上げれば良い」ので簡単ですが、「ゆっくり、引き上げる」際に揺れることもあります。
一度やってみるのが一番良いですが、絵で描いて頭でイメージしましょう。
そして、周囲には何もなく、広い部屋でじっくり実験できる状況を考えましょう。
いわば、「理想的な状態」を考えることです。
・時には、「極めてゆっくり動かす = 常につり合いが取れている」イメージ
・難しそうな時は「理想的な状況」で実験をしているイメージ
この「理想的な状態」を考えることは、小学生には難しいかもしれません。
男子小学生「理想的」って、
ちょっと難しいけど・・・
女子小学生もっと簡単に、
考えられたらいいけど・・・
別の言葉で表現すれば、「自分の都合の良いように」でも良いでしょう。
男子小学生「僕の都合の良いように」
で良いの？
「自分の都合の良いように」が、状況から全く異ならなければ、良いでしょう。
「理想的な状況」を考えることは、中学以降の物理・化学などで、よくあります。
中学生以上の方は、化学の気体で「状態方程式：PV =nRT」を教わります。
その時、「理想気体とする」という前提が必ずあります。
それは、本当は「気体は状態方程式：PV =nRTには厳密にはならない」からです。
「厳密にはならない」ですが「まあまあなる」のです。
「まあまあ合っている」ので、「大体のことがわかる」「まあまあ」では「=」にできません。
数学的に「=」は「辺の両側が等しい」ことを示します。
そこで、「余計なことは置いておいて、簡単にして（理想状態）、方程式を=で結んで考えましょう」です。
算数で「二つの図形・点が動く」時、「一つの図形の動きを止めて考える」ことがあります。
これも、「自分の都合の良いように状況を考える」一つの方法です。（上記リンク）
同様に、動く点・図形が二つある時に、
塾講師「片方の点・図形を止める」のが
鉄則！
「片方を止める」と習った方もいるでしょう。
男子小学生うん。
あれ、ちょっとしっくりこないんだよね。
「片方の点・図形を止める」のは、本質的には「やや難しい」考え方かもしれません。
中学・高校数学でも頻出の「片方の点・図形を止める」考え方。
なぜ、難しく感じる方が多いかというと、「動いているのに、勝手に止める」からです。
男子小学生そう。動いているから
難しいのに・・・
男子小学生勝手に「止める」のが、
分かりにくい・・・
「動いているのを勝手に止める」から、分からなくなります。
例えば、「止める」ではなく「片方の点をゆっくり動かして、他方の点を高速で動かす」を考えましょう。
この高速というのは、非常に速い速さで「ゆっくり動いている点・図形が止まって見えるほど」です。
すると、事実上「片方の点が止まっている状況に近く」なります。
男子小学生そう考えると、
少し分かりやすいかも・・・
このように理科・算数（数学）などでは、「自分の都合の良いように」考える姿勢も大事です。
・「自分の都合の良いように」考える姿勢
・条件・制約などから離れない程度に、「勝手に速く・遅く」する
状況をまとめて考える：二つの状況を比較
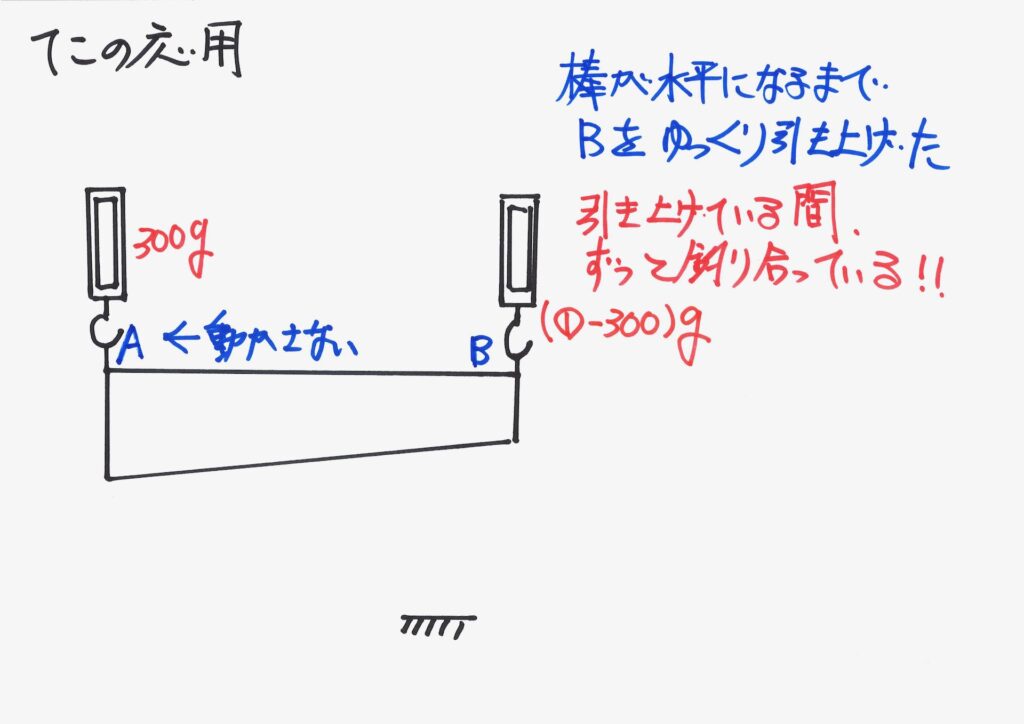
先に、Aを動かさないで、「Bをゆっくり=ずっとつり合っている状況」で引き上げました。
そして、今度はBを動かさないで、「Aをゆっくり=ずっとつり合っている状況」で引き上げました。
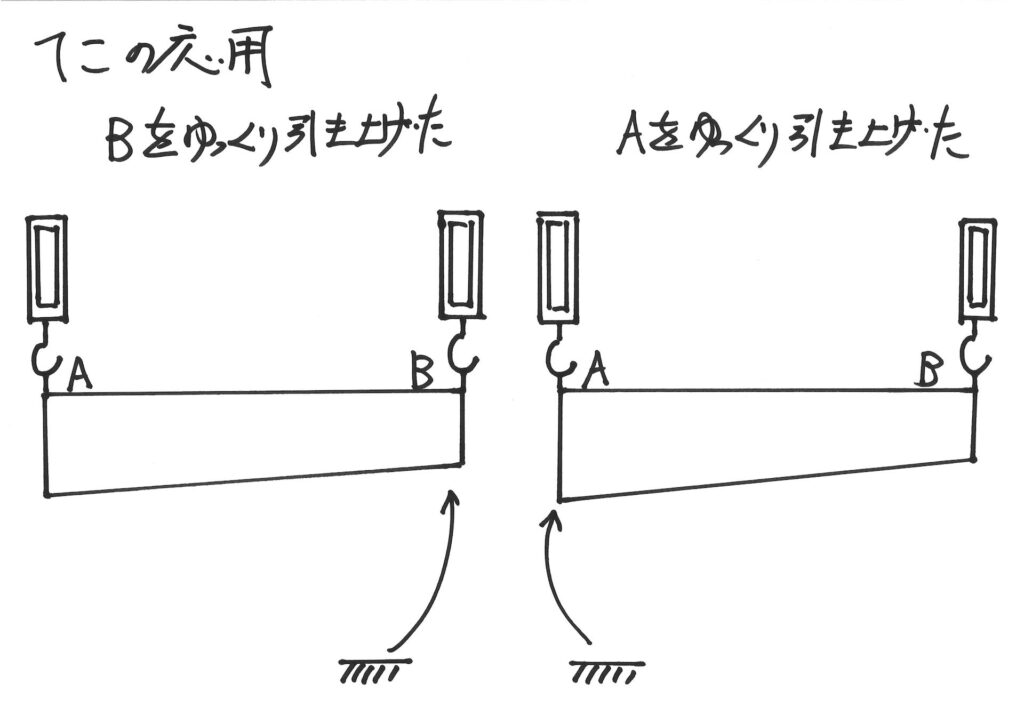
引き上げた結果の状況を、まとめてみましょう。
このように、「考えた状況を一つにまとめて比較する」ことは大事です。
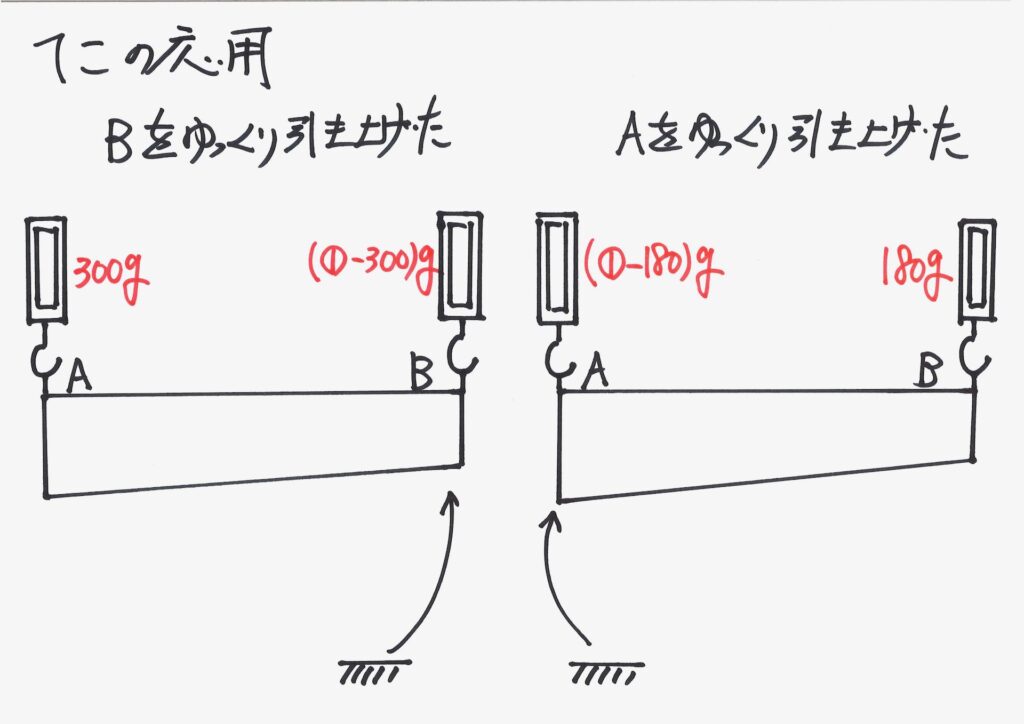
それぞれの「はかり」の重さが、分かりました。
男子小学生あっ！
ひょっとして・・・
女子小学生これって、
同じじゃないの？
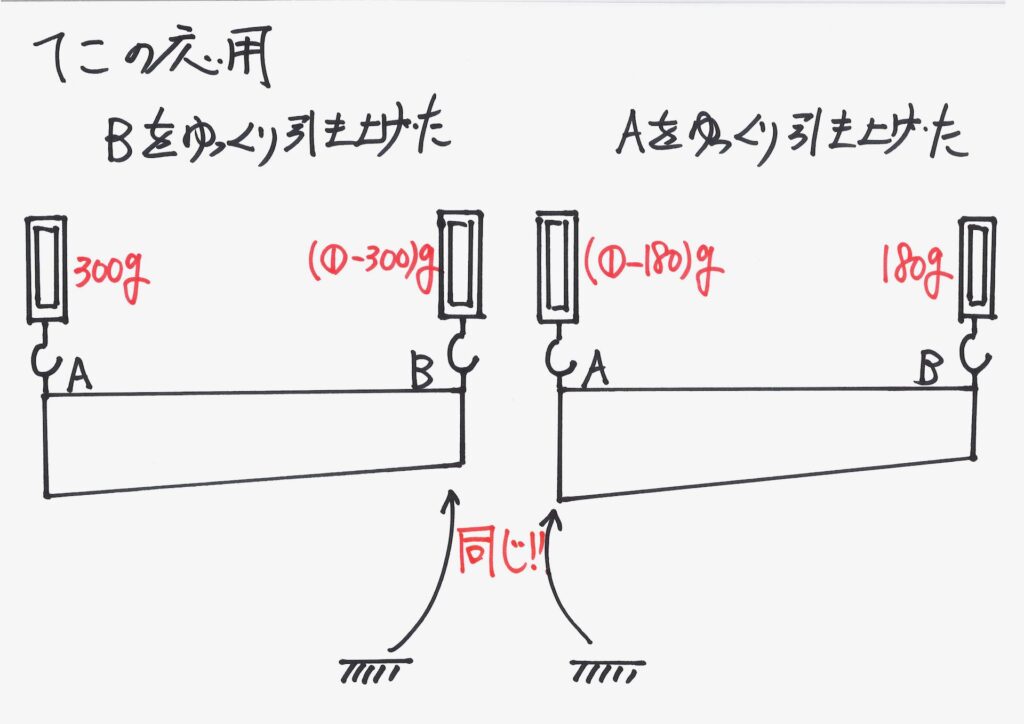
まさに「状況が同じ」はずです。
男子小学生ということは、
「それぞれ同じ」かな？
女子小学生同じになる
はずだね！
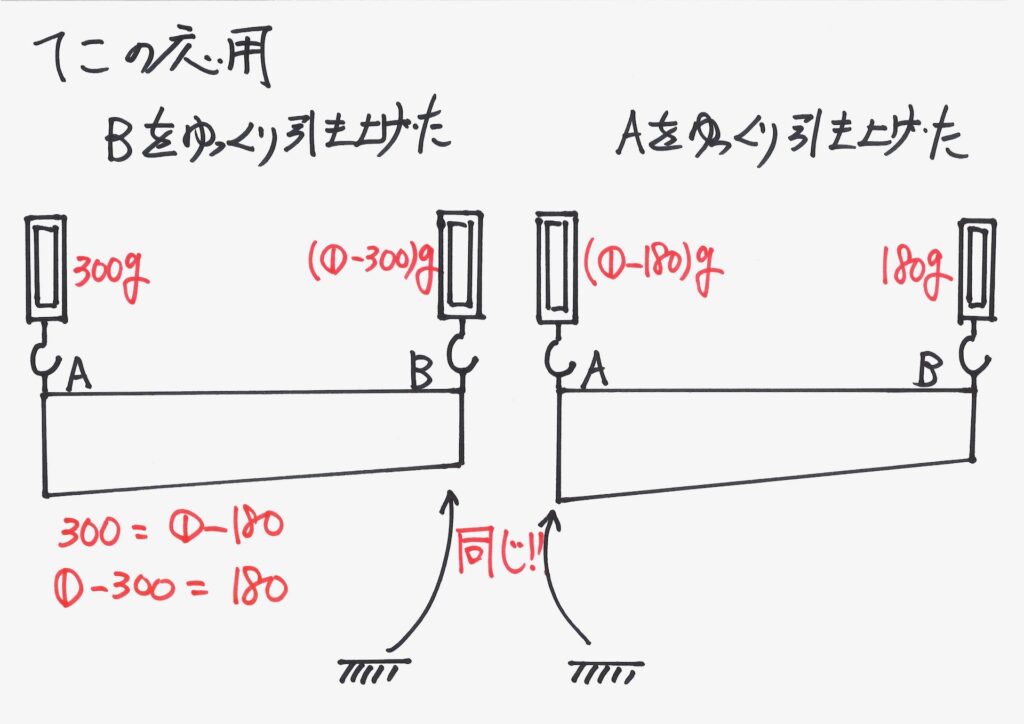
それぞれの「はかり」の重さを、比較してみましょう。
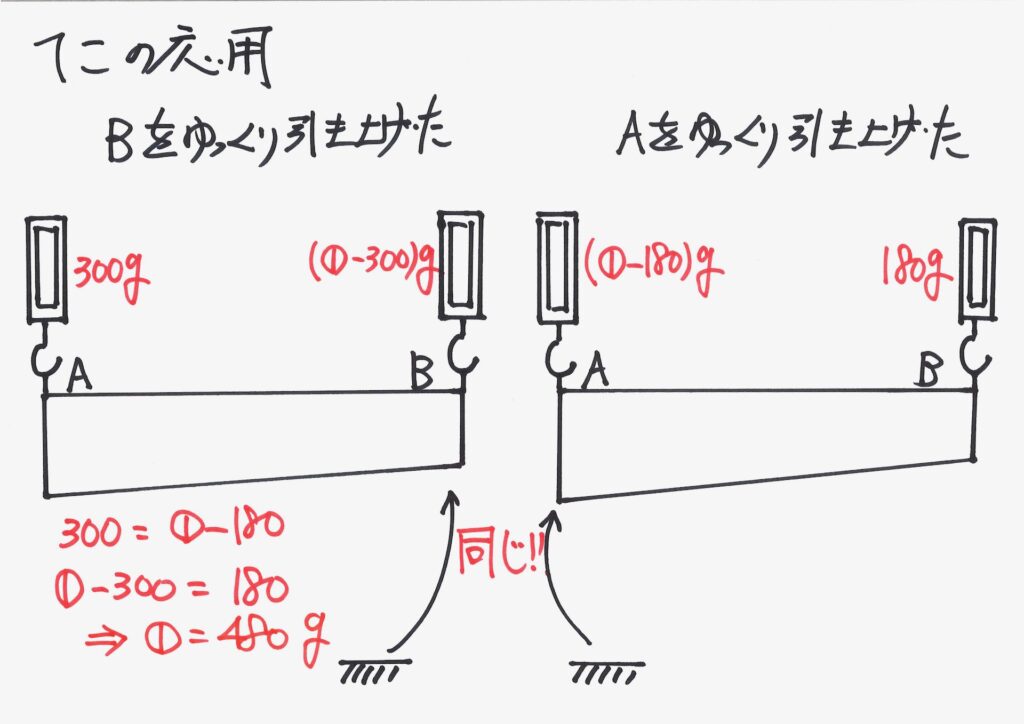
棒の重さ、棒が水平になるまで持ち上げた時の、A,Bの「はかりの重さ」も分かりました。
考え方を比較：似ている点と異なる点
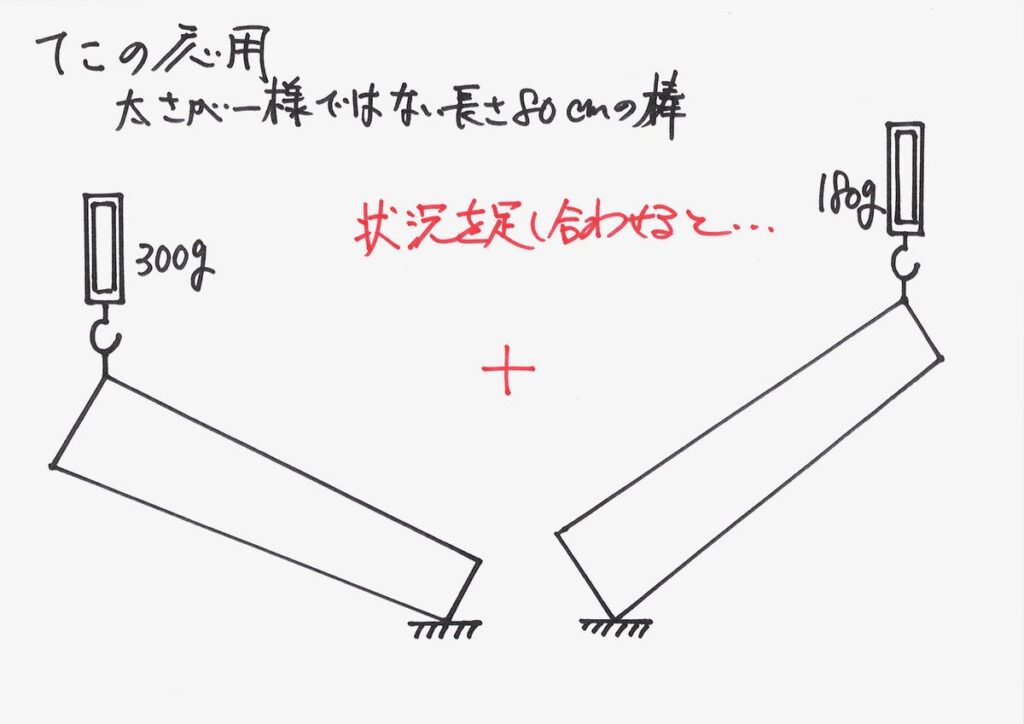
状況を「足し合わせる」「重ね合わせる」考え方をしました。
「足し合わせる」「重ね合わせる」のは、非常に大事な物理的考え方ですが、少し難しいです。
男子小学生でも、この「引き上げる」話は
分かりやすいよ！
女子小学生考え方が、
とても違うように感じる・・・
違うのは、どういうところでしょうか。
男子小学生「足し合わせる」「重ね合わせる」のは、
「すぐ」だよね。
女子小学生「足し合わせる」「重ね合わせる」のは、
動かしたりしてないね。
女子小学生分かれば、「足し合わせる」「重ね合わせる」方が、
早く出来るかも・・・
「足し合わせる」「重ね合わせる」はイメージできれば、その状況から瞬時に分かります。
男子小学生「ゆっくり動かす」のは、考えるのに
時間かかるけど・・・
男子小学生こっちの方が、
分かりやすいかな・・・
女子小学生「ゆっくり動かす」のも面白かったし、
分かりやすいから、両方の考え方が良いかも・・・
算数・数学や理科は、いくつかの異なる考え方・別解を学ぶと、理解が深まります。
そして、本質的な学力が上がり、成績も大きく上がるでしょう。
そういう時は、「何が違うかな？」とか「似ているところはないかな？」と考えましょう。
次回は下記リンクです。
