前回は「ててこの応用・太さが一様でない棒 2〜つり合いのイメージ・2つの状況と現象・足し合わせる・重ね合わせる・「像を重ねる」イメージ・重心と重さ・モーメントは「回転する力」〜」の話でした。
状況を足し合わせる・重ね合わせる=像を重ねる
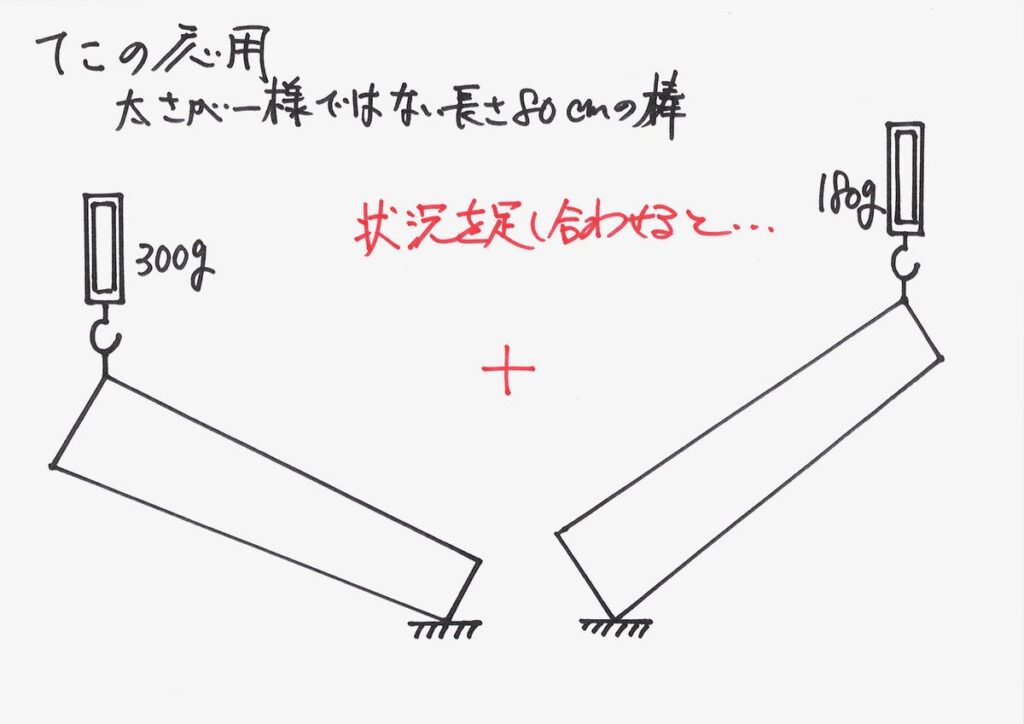
「太さが一様ではない」棒の左の端・右の端を、それぞれ持ち上げた状況です。
このように、同じ状況=「太さが一様ではない」棒があるに対して、二つの異なる状況になりました。
両端を持ち上げた時の状況を、「足し合わせる」あるいは「重ね合わせる」話をしました。
上の二つの「異なる状況を足し合わせる・重ねる」と、
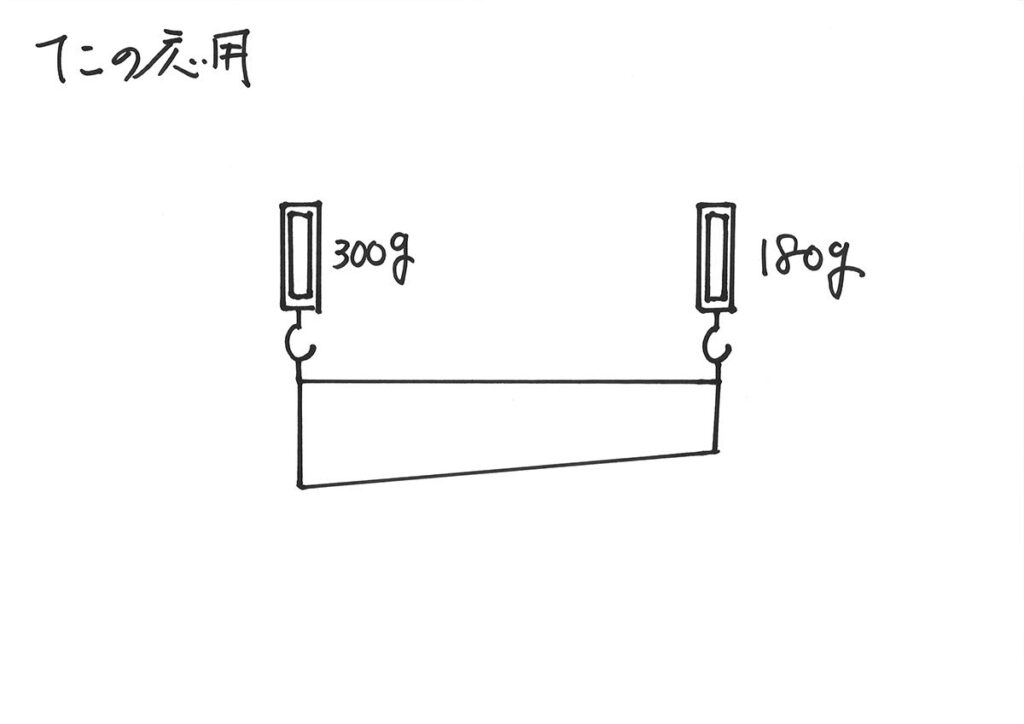
スッと重そうな「太さが一様ではない棒」が持ち上がるイメージです。
状況を「足し合わせる・重ね合わせる」ことは、非常に本質的な考え方です。
・様々な理科（物理）の現象で、同じ対象に対して、2つの異なる状況を考えることができる
・「足し合わせる」「重ね合わせる」は「像を重ねる」イメージ
非常に本質的で大事な考え方ですが、「しっくりこない」人が多いと思います。
こういう時に「理解できない」と、
男子小学生分からない・・・
なぜだろう・・・
男子小学生分からないから、
これ以上進まない・・・
「分からない」と自信がなくなることがあります。
あるいは、
女子小学生分からないけど、
まあいいや！
女子小学生こういうことだって、
丸暗記すればいい！
「暗記すれば良い」という考え方の人もいるでしょう。
前者の方のように、「進まない」と止まってしまわずに、
男子小学生完全には分からないけど、
そんなような気もする・・・
「大体の理解」でも良いでしょう。
後者の「丸暗記」は「良い・良くない」の議論がありますが、「丸暗記」で解ける問題もあります。
女子小学生テストでは、点数を取ることが
大事だから・・・
女子小学生丸暗記でもなんでも
試験が出来た方が良いと思う！
特に「答えだけ」や「選択肢」の問題だと、「答えが分かるかどうか」で点数が明確に分かれます。
そのため、「考え方をしっかり理解」するのがベストですが、多少「暗記」になることもあるでしょう。
このあたりは、子どもそれぞれ「臨機応変に」が良さそうです。
理科の生物・地学分野などは、「知っていなければ解けない」問題が多いです。
いわゆる「知識を問う問題」であり、「丸暗記」している方が強いのです。
男子小学生結局、全部「丸暗記」した方が
早いんじゃない？
理科の物理・化学分野は、「理解すること」を念頭に、「理解しながら習得」を目指しましょう。
その過程で、
男子小学生ちょっと分からないけど、
まあ、こういうことだと覚えておこう！
「理解と暗記」を意識しすぎずに、勉強を進めるのも手です。
音読の大事さ：少しずつ理解
最近は、学校・塾で「音読する」は、それほど多くないです。
昔の寺子屋・藩校、あるいは郷中教育では、中国の古典である四書五経を子どもたちは学びました。
例えば、論語なら、
寺子屋の先生まずは
一緒に読んでみよう！
寺子屋の先生子、
曰く（いわく）・・・
江戸時代の子ども子、
曰く（いわく）・・・
寺子屋の先生学びて思わざれば、
くらし・・・
江戸時代の子ども学びて思わざれば、
暗し・・・
寺子屋の先生思うて学ばざれば、
あやうし。
江戸時代の子ども思うて学ばざれば、
あやうし。
論語には「読んで意味が分かる」内容もありますが、多くは「難しい内容」です。
大人が読んでも「良く分からない内容」が沢山あります。
上の例の、「学びて思わざれば暗し、思うて学ばざればあやうし。」の意味は比較的簡単です。
「簡単」と言っても、その奥は非常に深いのです。
大人、あるいは、50歳を過ぎた方でも「どこまで本質を理解できているか」は不透明なほどです。
論語を読んだ子どもたちは、
江戸時代の子どもなんだか、
良く分からないけど・・・
「よく分からない」と思いながらも、
江戸時代の子どもみんなと一緒に声出して
勉強するのが大事なのかな・・・
こんな感じだったでしょう。
そして、繰り返し、
江戸時代の子ども学びて思わざれば、
暗し・・・
江戸時代の子ども思うて学ばざれば、
あやうし。
音読しているうちに、
江戸時代の子どもなんか、
少し分かった気がする・・・
少しずつ理解を進めていったのでしょう。
そして、江戸時代は、現代のように「試験・テストが度々ある」状況ではありませんでした。
それでも、このように基礎を固めた人々の中に、大勢の優れた人物が登場しました。
現代の「頭が良い・優秀」と同じように非常に優れた頭脳を持っていた適塾卒業生たち。
あるいは、幕府側の優れた要人たちもまた、非常な勉強家で優秀でした。
テスト・試験に対する姿勢が、全く異なる現代と江戸時代。
比較は難しいですが、当時は「当時なりに体系化された学問」を懸命に学んだ方々がいました。
そして、その方々は、若き頃から飛躍していったのです。
書いたり、声に出すことは、非常に大きな学びにつながります。
この「重ね合わせる」イメージは、分かりにくいようでしたら、描きながら、
男子小学生ここが、
こうなって、重なって・・・
声に出しても良いでしょう。
学校・塾では「声に出す」のは、遠慮があるかもしれません。
そこで、自宅等で勉強しているときは、遠慮なく、声に出してみましょう。
そのように、声に出しながら描くと、身体全体で学ぶ感じになり、やっているうちに
男子小学生なんか、
分かった気がしてきた・・・
理解が進むことがあるでしょう。
状況をイメージ：棒が机に乗る点
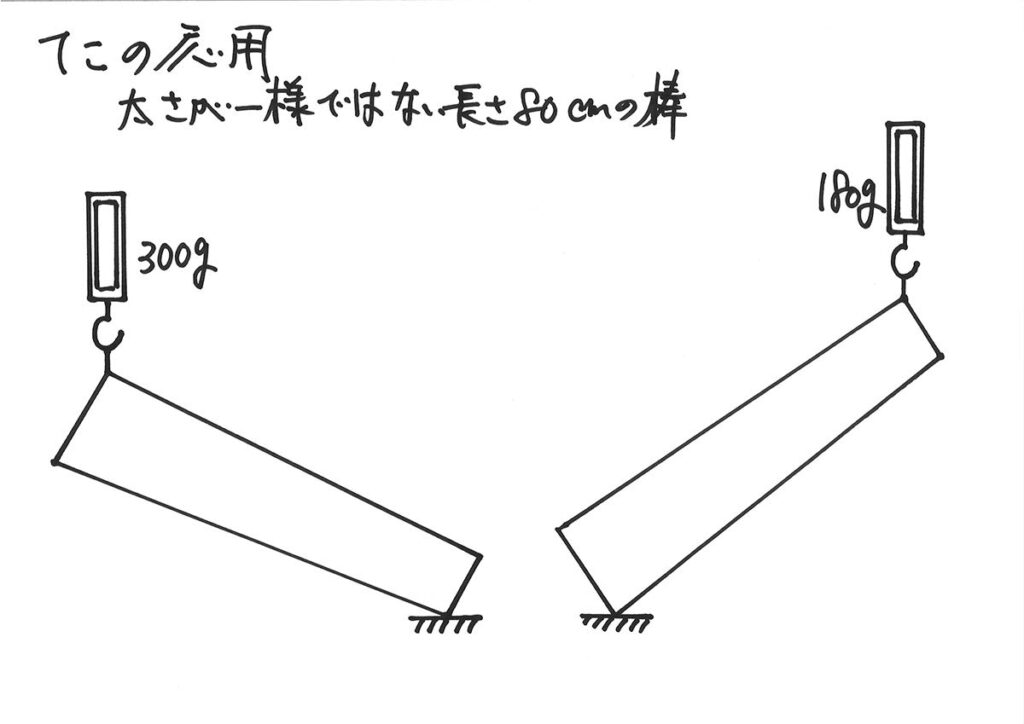
「重ね合わせる」考え方とは、異なる考え方をしてみましょう。
少し算数的に考えて、この「太さが一様ではない」状況を理解してみましょう。
男子小学生そもそも、
棒の重さが、まず分からない・・・
男子小学生棒の重さがわかれば、
あとはわかるんだけど・・・
「とっかかりが分からない」人も多いでしょう。
算数で「分からないモノ」が登場したら、いつもやることは、
男子小学生①とかで、
「分からないモノ」を考える！
「分からない」時は、算数と同様に未知数を設定しましょう。
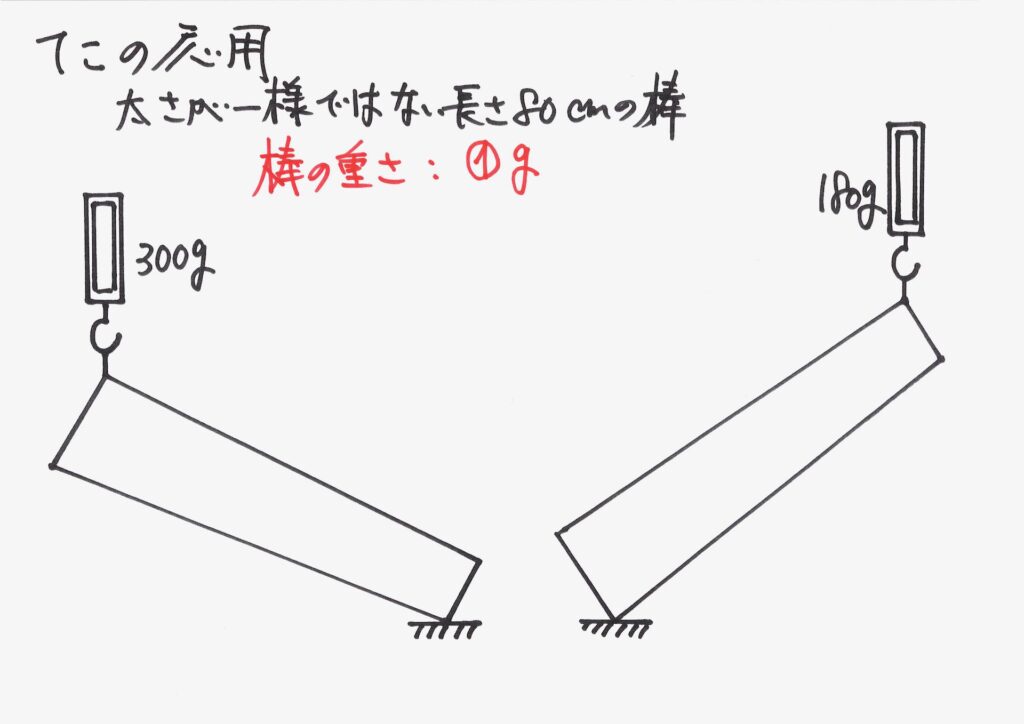
「棒全体の重さが①g」と考えます。
ここで、左側を持ち上げたら300g、右側を持ち上げたら180gです。
そして、「この①を求めよう」と考えましょう。
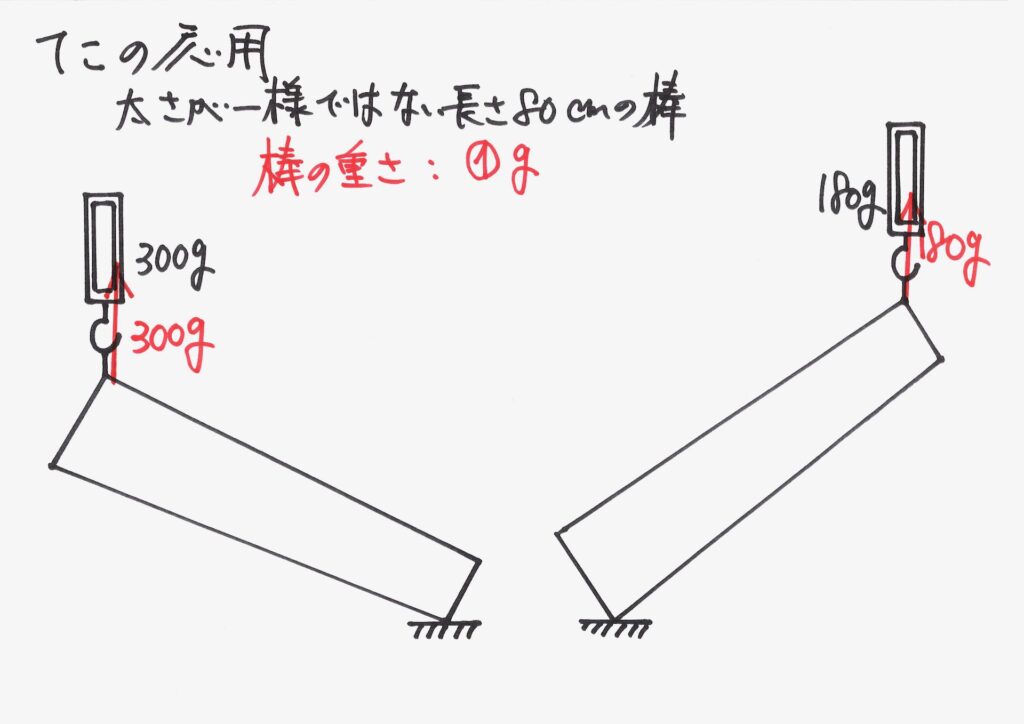
まず、引き上げている部分における、「力のつり合い」を考えます。
両側で300g、180gの重さとなっているので、「棒はそれぞれ300g、180gで引き上げている」です。
矢印で上向きに「棒にかかる力」を考えます。
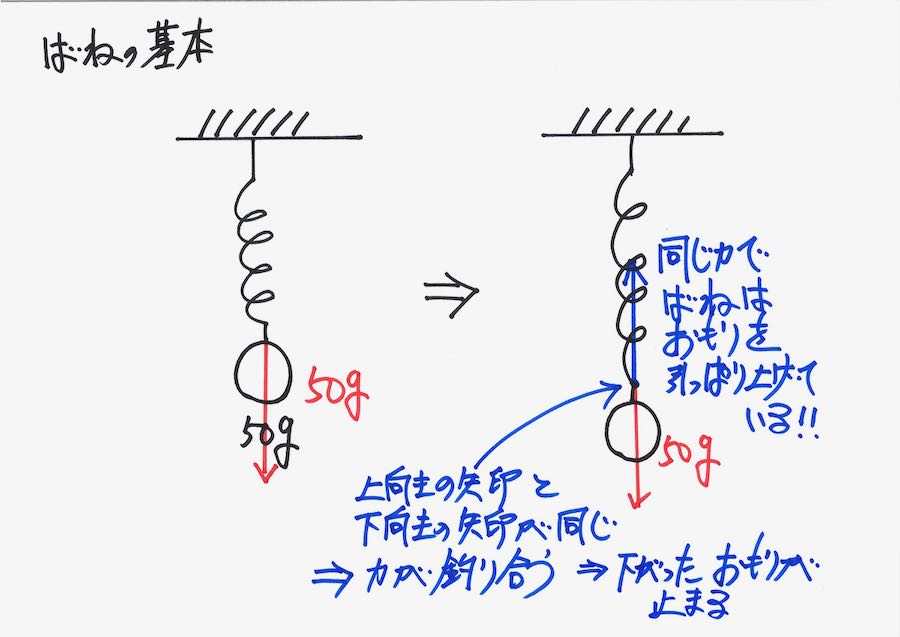
重さの「はかり」は「電子はかり」もありますが、基本的にはバネが内蔵されています。
そして、内部のバネが伸びてつり合っている状況をイメージしましょう。
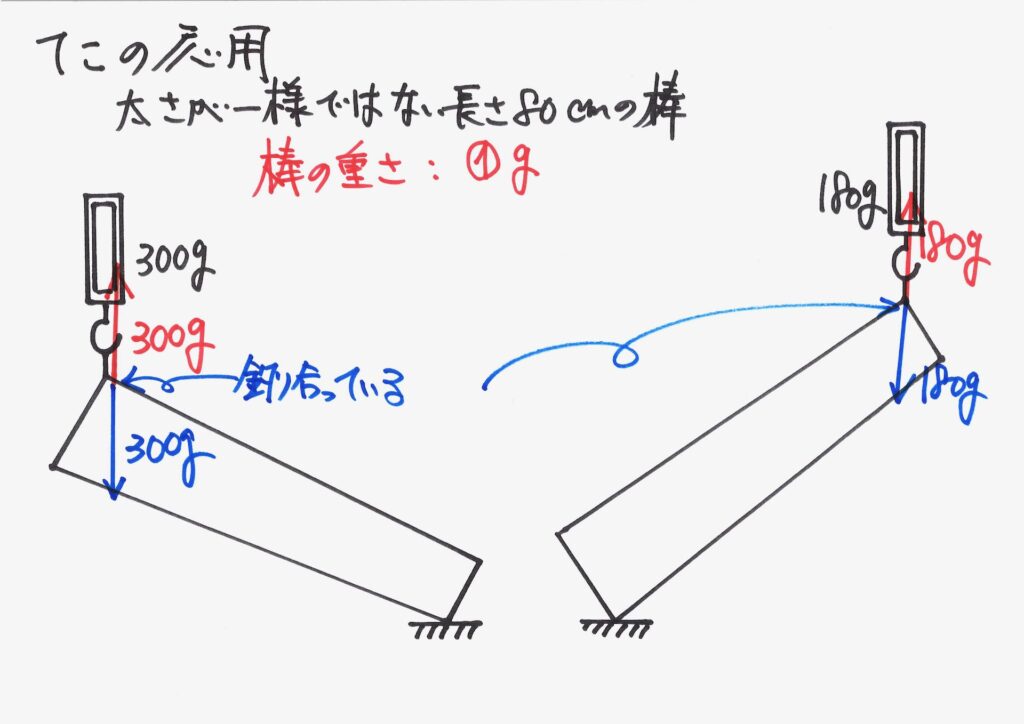
ここで、引き上げている「はかり」と棒の引っ掛けている点には、それぞれ「重さ」がかかっています。
左端の点で、「300gの重さがかかり、300gの力で引き上げて」つり合っている」のです。
右端の点で、「180gの重さがかかり、180gの力で引き上げて」つり合っている」のです。
これらは「下向きにかかる棒の重さ（重力）の一部」です。
「下向きにかかる棒の重さの一部」は、それぞれ同じ300g、180gで釣り合っています。
これで、「はかりと棒のつながる点」は釣り合っています。
女子小学生うん・・・
これは分かったよ。
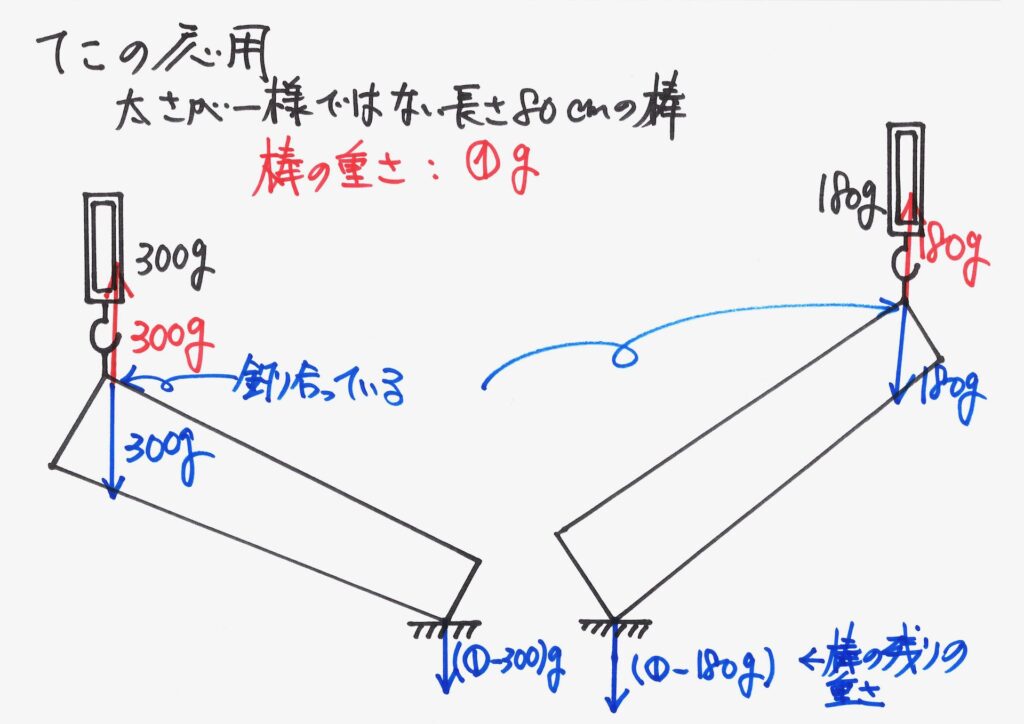
では、次に棒のもう片方を考えましょう。
問題では、棒をはかりで持ち上げていて、その反対側に関しては触れていないことがあります。
ここでは、「机に乗っかっている」と考えます。
女子小学生問題に書いてないこと
だけど・・・
女子小学生前にも
似たことがあったけど・・・
女子小学生条件が変わらなければ、
自分で考えれば良いのかな・・・
男子小学生ここは「机」でも
「床」でもいいのかな？
ここは「机」でも「床」でも、あるいは少し高さの低い「タンスの上面」でも良いです。
「何かに乗っかっている」ことを、実際にイメージしましょう。
棒からは、机に向かって下向きに「残りの重さ」がかかります。
このように具体的に、二つの状況に対して、様々な力を描いてみました。
上の「様々な力がかかっていて、机にかかる重さ」を「反対側のはかりで担う」イメージです。
男子小学生こうして、
具体的に矢印で力を描くのは、分かりやすいね。
「分からない」時は、手を動かして、色々と試行錯誤してみましょう。
男子小学生あれ？
なんか変だよ・・・
男子小学生棒と机のつながる点が、
釣り合ってないよ。
女子小学生そうだね。
両方とも下向きの力しかかかってない・・・
女子小学生すると、この点は
「どんどん下に行ってしまう」ことになるから・・・
女子小学生それって
変だね・・・
電流が回路を一周するときに、「元の高さ（電圧）まで落ちないとどうなるか」を考えました。
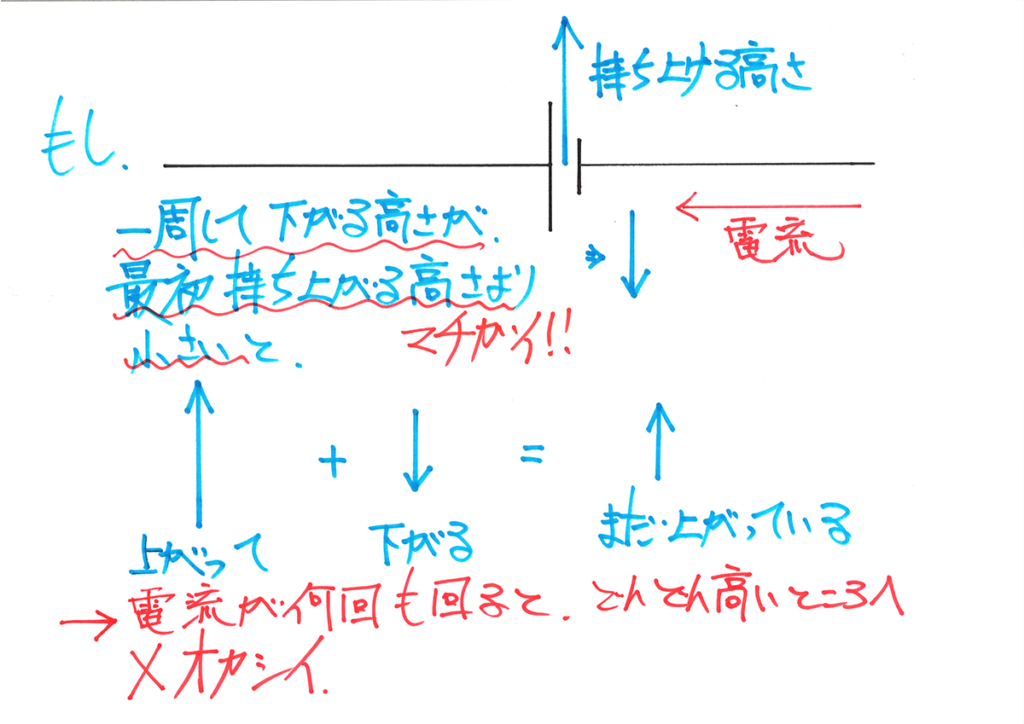
「どのような状況なら、釣り合うか」を考えてみましょう。
次回は下記リンクです。
