前回は「てこの応用・太さが一様でない棒 1〜・類似点と理科への探究心・全ての棒の点でのつり合い・重ね合わせる=二つの状況を足す・矢印で重さを表現〜」の話でした。
つり合いのイメージ：2つの状況と現象
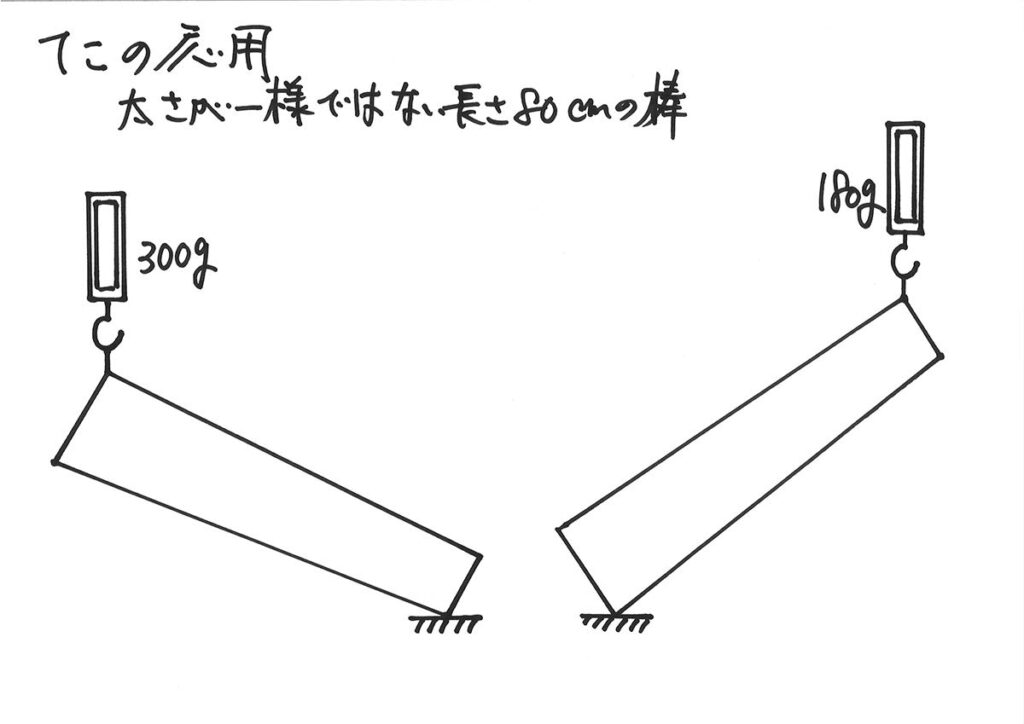
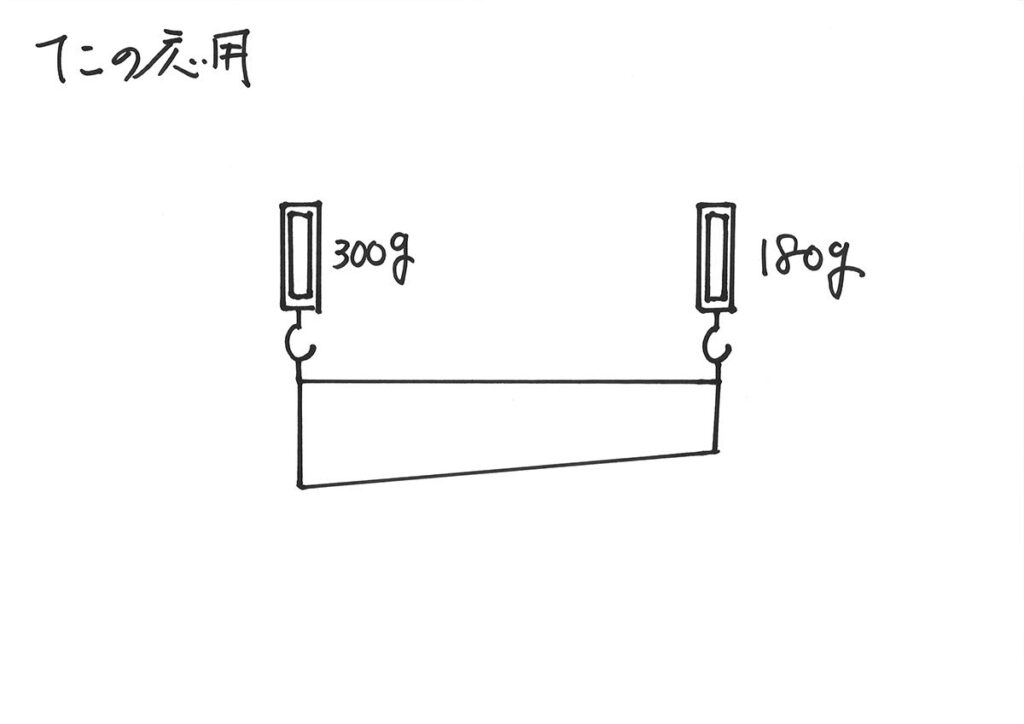
太さが一様（同じ太さ・密度）ではない「棒・てこ」の問題を考えてみましょう。
ここで特徴的なのは、「左端を引き上げている」状況と「右端を引き上げている」状況があることです。
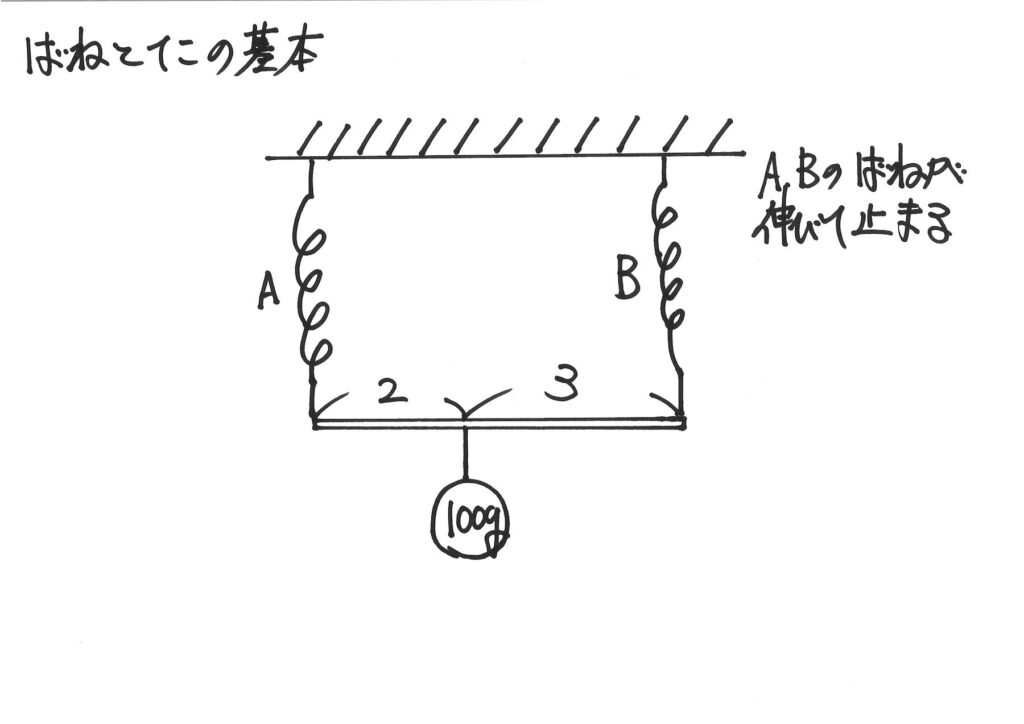
太さが一様である棒・バネの問題が多いです。
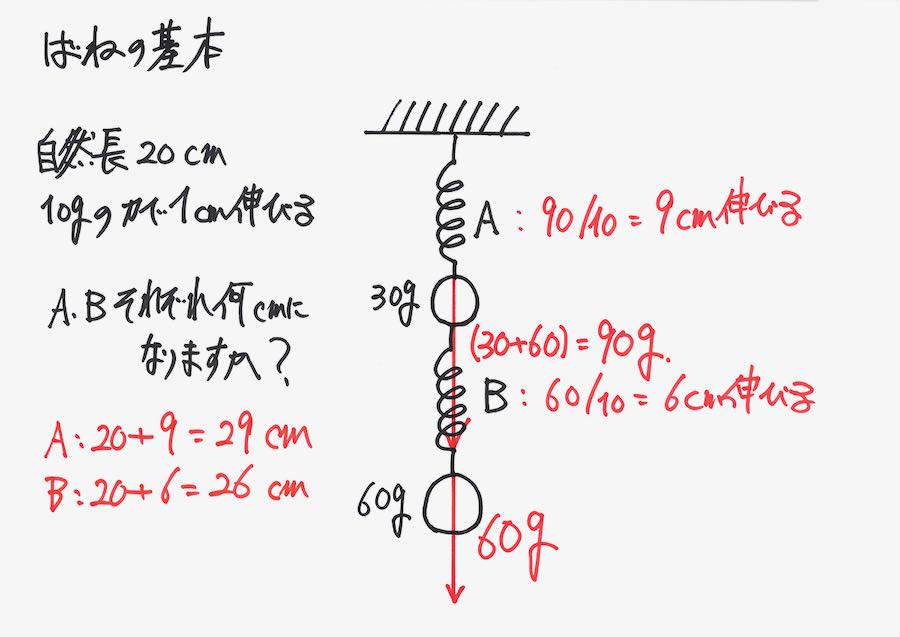
バネが直列などで結ばれている問題もあります。
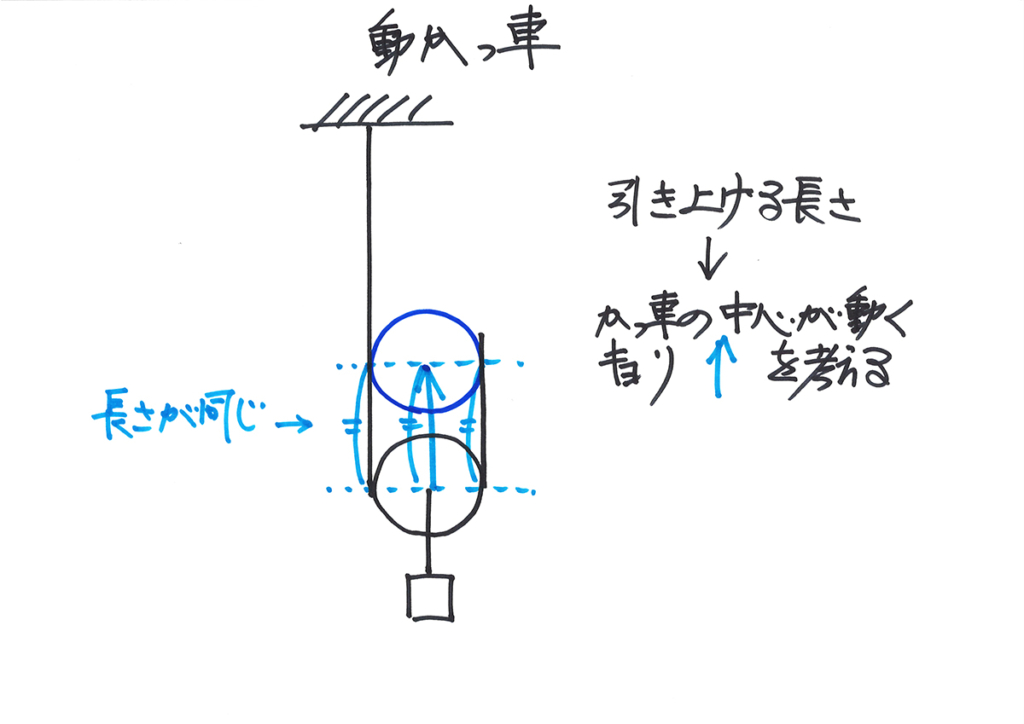
動かっ車・定かっ車の問題もありますが「考える状況は一つ」であることが、ほとんどです。
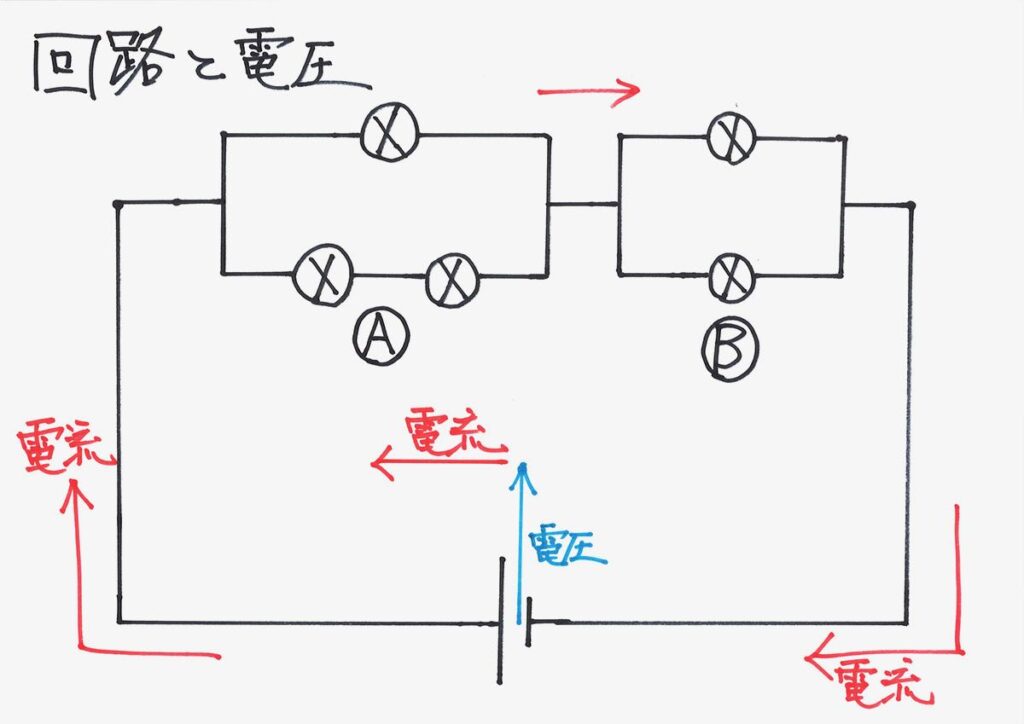
バネ・てこ・かっ車などが「力・重さ」を対象とするのに対して、電流・電圧が対象の電気の問題。
考える対象は異なりますが、「ある理科（物理）の現象」であることを考えると考えましょう。
その時、これらはいずれも「一つの状況・現象」です。
これに対して、「太さが一様でない棒」を考えるとき、多くは「2つの状況・現象」を考えます。
男子小学生確かにそう・・・
突然、二つ出てきて・・・
男子小学生なんだか、
分からなくなってしまう・・・
「左端を引き上げる」と「右端を引き上げる」の2つの状況・現象を足し合わせる話をご紹介しました。
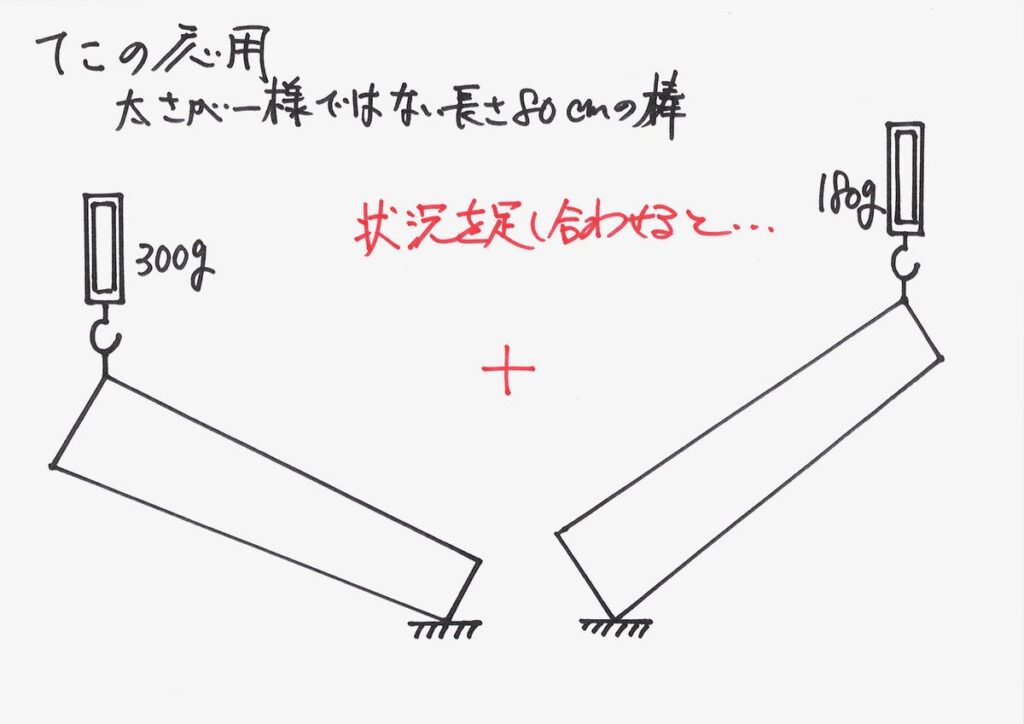
足し合わせる・重ね合わせる：「像を重ねる」イメージ
「足し合わせる」考え方は「重ね合わせる」とも表現し、とても大事な考え方です。
2つの状況・現象を「足し合わせる」あるいは「重ね合わせる」と、上のようになります。
ここで、パッとこれが分かるのは、難しいことでもあります。
女子小学生「足し合わせる」「重ね合わせる」は
分かるけど・・・
女子小学生なぜ、「足し合わせる」「重ね合わせる」と
こうなるのか、ちょっとピンとこない・・・
女子小学生私って、理科のセンスがあまり
ないのかな・・・
考え方としては、「足し合わせる」「重ね合わせる」は難しくはなさそうです。
一方で、状況・現象を「足し合わせる」「重ね合わせる」しっかりイメージ・理解するのは難しいです。
こういうことを「理解できるかどうか」には、センスは大して関係ありません。
「足し合わせる」「重ね合わせる」考え方は、中学・高校物理でも大事な考え方です。
中学受験生は、「なんとなく分かる」くらいで良いでしょう。
女子小学生大体、
でいいの？
男子小学生「基本をしっかり」という
姿勢が大事なんじゃないの？
この「足し合わせる」「重ね合わせる」考え方は、一つの「基本的考え方」です。
そのため、「しっかり理解できること」が望ましいです。
一方で、これらの「基本的考え方」のイメージは、完璧を目指さない方が良いかも知れません。
ある程度は、「大体わかる」「こんな感じかな」でも良いので、イメージをしっかり持ちましょう。
・「基本的考え方」はクリアなイメージを持つようにして、完璧を目指さない
・「大体こんな感じ」でも良いので、公式だけではなく具体的イメージを持つ
「足し合わせる」「重ね合わせる」考え方は、「力・重さ」等に限りません。
電流・電圧などでも、状況によっては考えられます。
電気の応用問題で、「足し合わせる」「重ね合わせる」考え方が出題される可能性はあります。
「足し合わせる」「重ね合わせる」時は、「像を重ねる」イメージが良いでしょう。
・様々な理科（物理）の現象で、同じ対象に対して、2つの異なる状況を考えることができる
・「足し合わせる」「重ね合わせる」は「像を重ねる」イメージ
男子小学生「像を重ねる」
イメージなら分かるかも・・・
女子小学生ちょっと分かりやすく
なったかも・・・
二つの状況を、「影のように」考えてみましょう。
みなさんが校庭で友達と一緒にいる時に、お互い同じ向きに影ができます。
「影の長さ・面積の問題」が算数でありますが、あのイメージで、足して・重ねてみましょう。
この意味では、算数と理科は非常に親近感のある関係にあります。
てんびん算・てこは、算数も理科も同じ考え方です。
「算数と理科（物理分野）は、お友達」なのです。
お互いをイメージすると算数・理科（物理分野）の学力が上がるでしょう。
・算数と理科（物理分野）は似ている面があり、お友達の関係
・理科の「重ね合わせる」イメージは、算数の影の問題で「足し合わせる」イメージ
重心と重さ：モーメントは「回転する力」
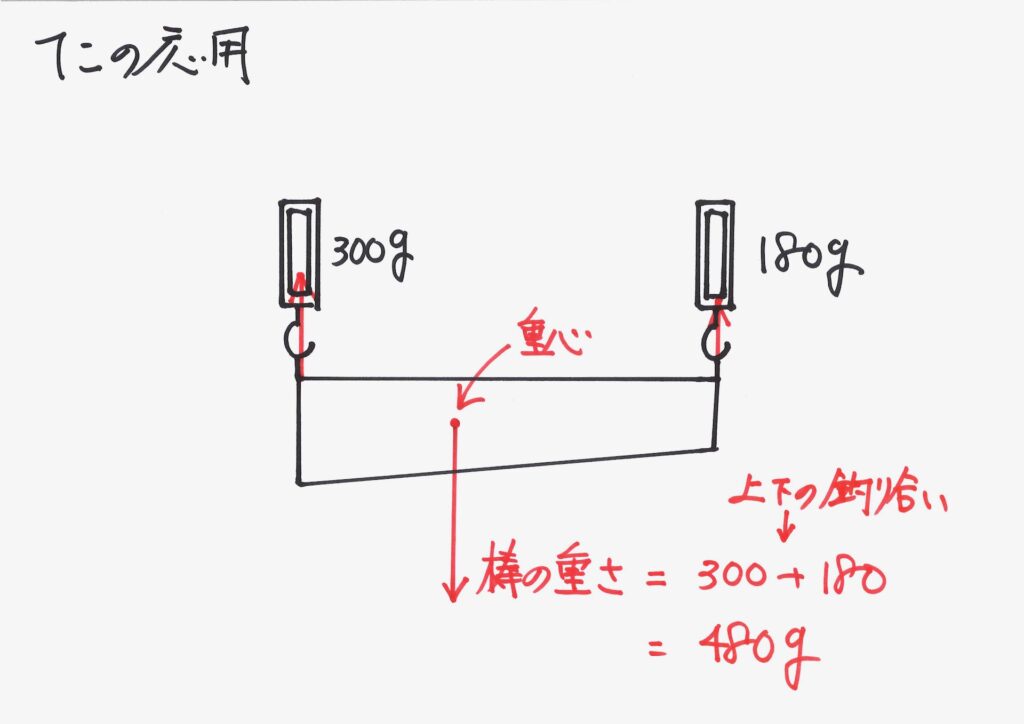
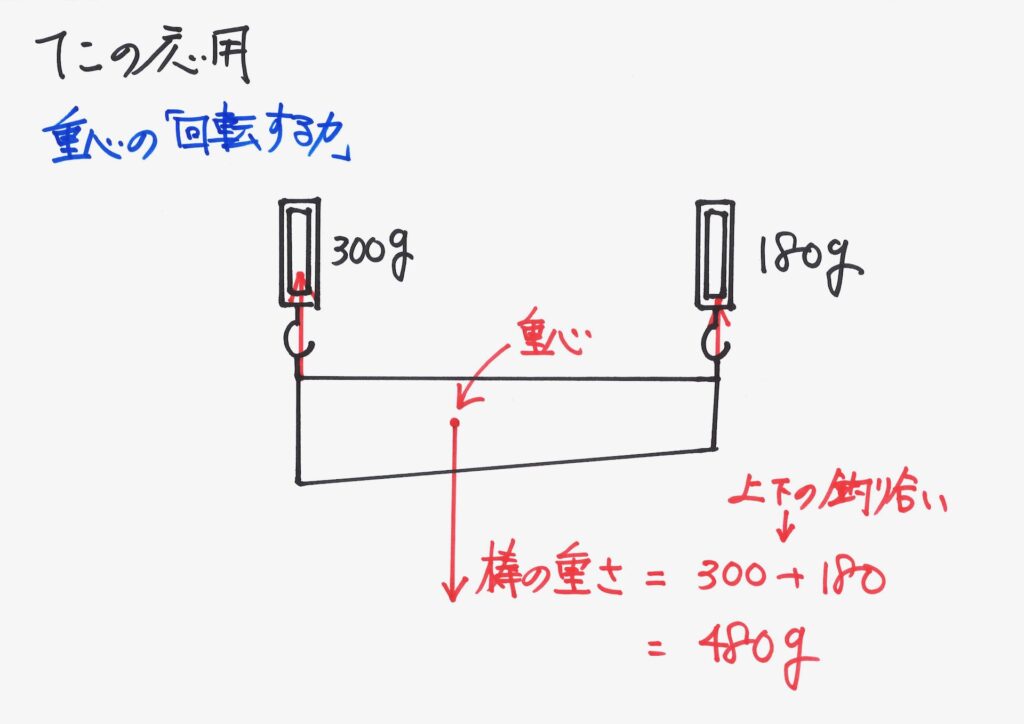
状況を足し合わせて、棒の重さが求まりました。
「重ね合わせ」「足し合わせ」したので、重さも「足し合わせ」ることになります。
ここで「重心」を考えましょう。
男子小学生なぜ、「重心を考える」必要が
あるの？
男子小学生「重心を考えない」考え方は
あるの？
こういう問題では、重心が出てくることが多いです。
そして、「なぜ、重心を考えるのか？」という姿勢はとても大事です。
重心を考える理由は、一定の大きさのモノが登場すると「重心は、とても大事」だからです。
理科・物理では、本当は「大きさがある」モノを「点」などで考えることがあります。
それに対して、一定の大きさのモノは中学・高校の物理では「剛体」と呼びます。
女子小学生剛体
って何？
言葉は覚えなくて良いので、「そういう言い方もある」くらいで良いでしょう。
「ある大きさがある」モノ・「一様でない」モノを考える時、重心は極めて大事です。
重心を考えずに先に進めることは、「ほとんどない」と言っても過言ではないでしょう。
「回転する力」を考えてみましょう。
重心とは「モノの重さが一点に集まっていると考えられる」点です。
「全ての点（場所）に重さがある」棒は、「重さが重心一点に集まっている」と考えます。
・モノ（棒など）の重さが一点に集まっていると考える点
・重心の位置は、モノ（棒など）の形によって変わる
・モノ（棒など）が、同じ太さ・密度（一様）であれば、重心は中心
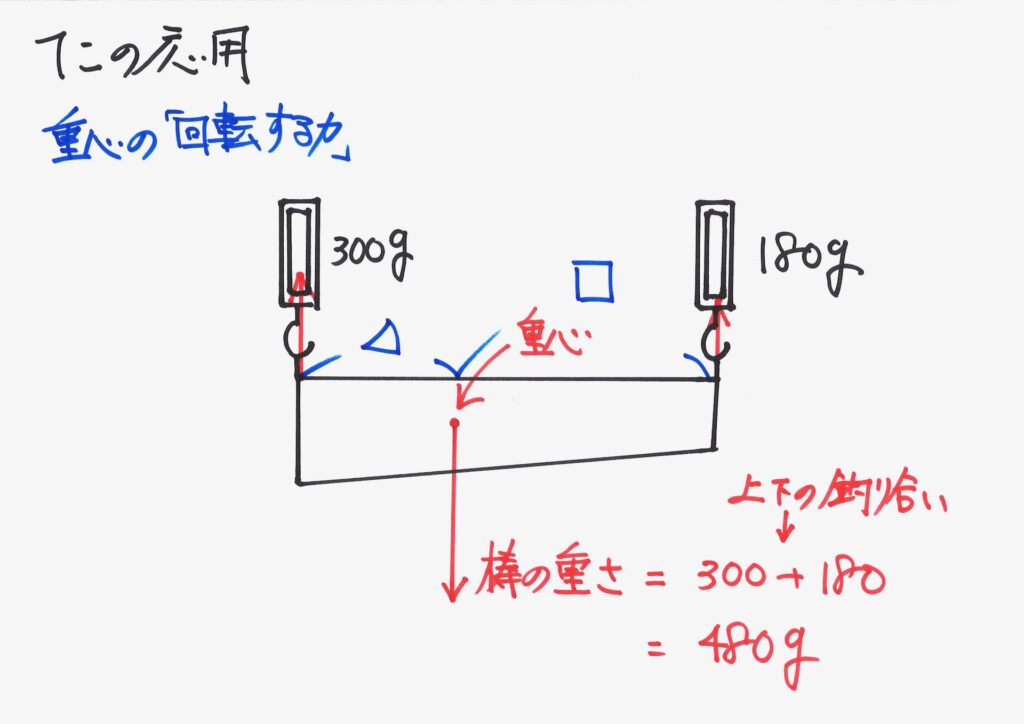
重心から左右の端までの距離を、それぞれ△・□と置きましょう。
これは、「◯・△」でも、「◯・□」でも自分が好きなように設定しましょう。
棒の長さは80cmですから、「△ : □の比」を求めます。
算数でも比の問題は沢山ありますが、理科では「比は重要」です。
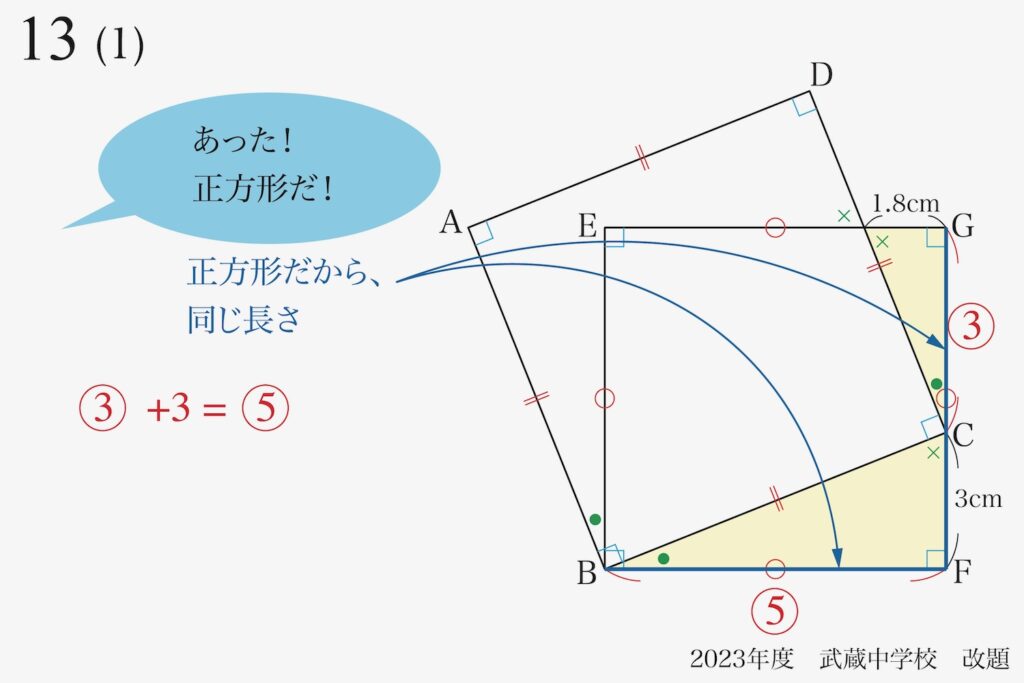
図形問題は、比を押さえれば、ほとんどの問題が解けます。
相似形や同じ図形などを考えて、辺や面積の比を考えれば、解けることが多いです。（上記リンク）
この時「どの比に着目するか」が大事ですが、この点は理科は分かりやすいです。
補助線などで「考える対象」が隠れていることが多い算数。
それに対して、理科は目の前の状況として「現れていることが多い」です。
・算数は、図形問題などで、隠れている対象含め「どの比に着目するか」を考える
・理科は、目の前の現象の棒・電線などのモノの長さなどに注目
理科の問題で、長さなどを求める場合は、長さを直接考えるよりも、
男子小学生比が
分かるかな・・・
「比が分かるのは、どこかな」と考えましょう。
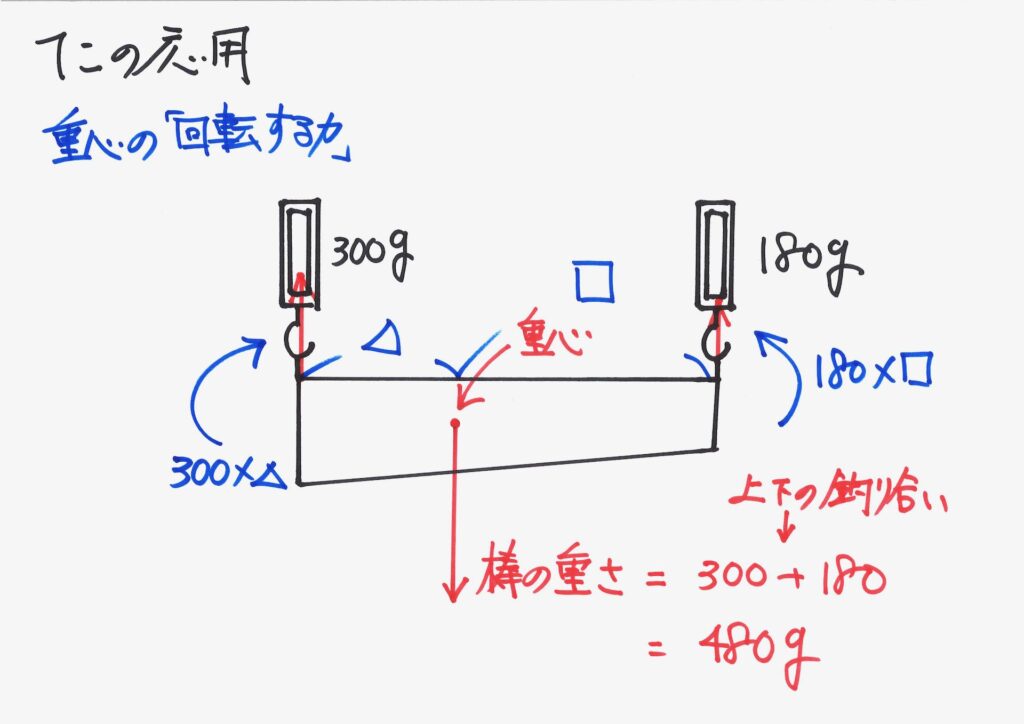
重心の周りで、「回転する力」を考えましょう。
二点で吊り下げられて「釣り合っている」ので、棒のどの部分でも「釣り合いが取れている」のです。
棒のどの部分（点）でも、「上下の重さの釣り合い」と「回転する力の釣り合い」が取れています。
どの点で考えても良いですが、「力の掛かっている点」で考えるとシンプルです。
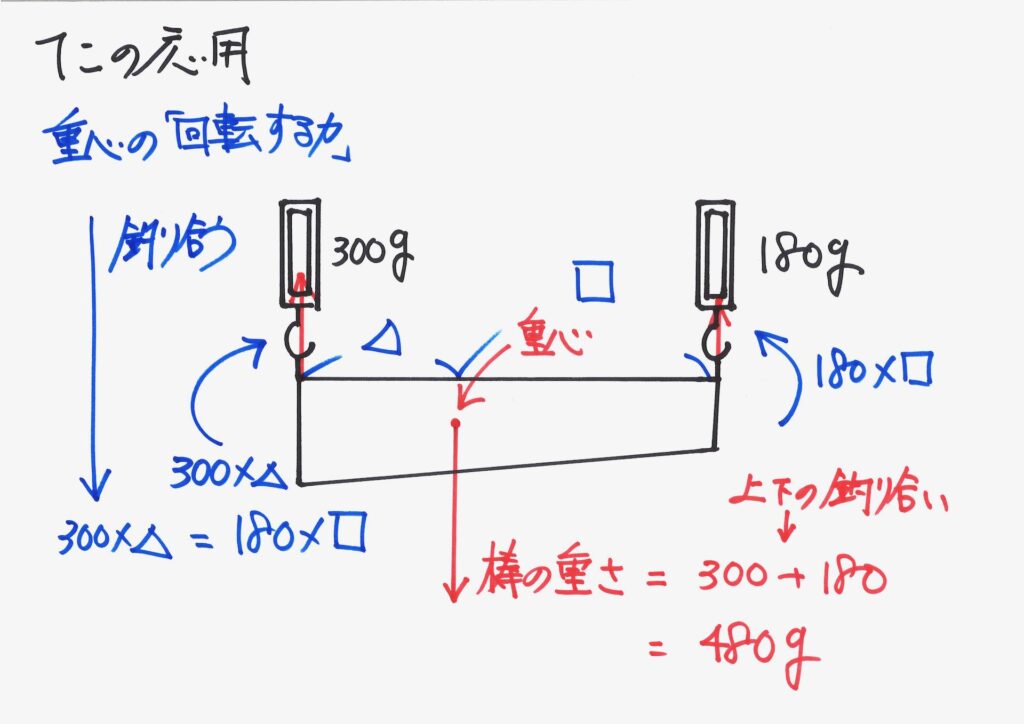
重心の周りの、反時計回りと時計回りの「回転する力」が釣り合っています。
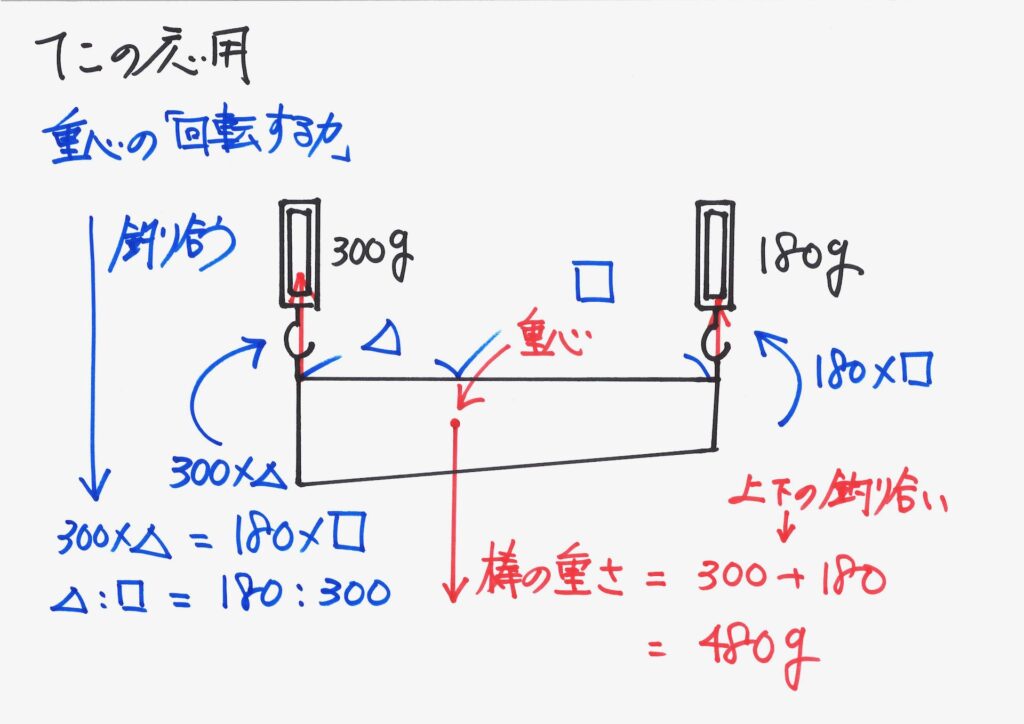
「掛け算して同じ（等しい）」ですから、「△ : □の比」が分かります。
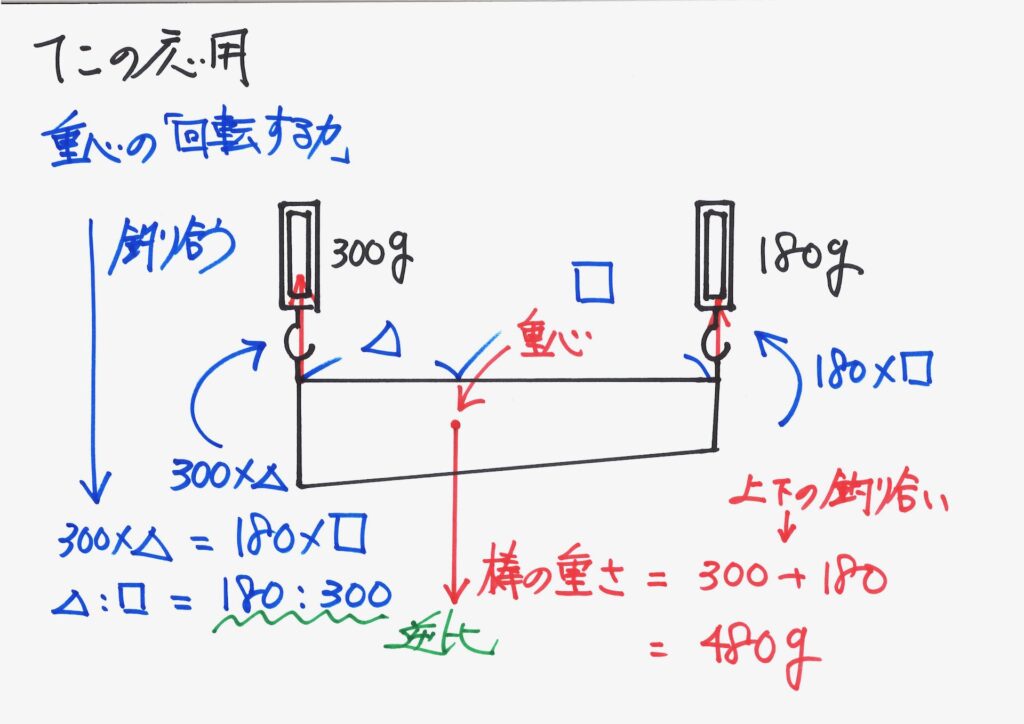
「△ : □の比」は、重さの逆比です。
整理して、「△ : □ = 3 : 5」で、合計80cmですから、それぞれ求まります。
男子小学生これで、
逆比の理由が分かったよ。
女子小学生これなら、「逆比」と暗記しなくても
分かる！
女子小学生そういえば、
バネと棒の時と、似ているかも・・・
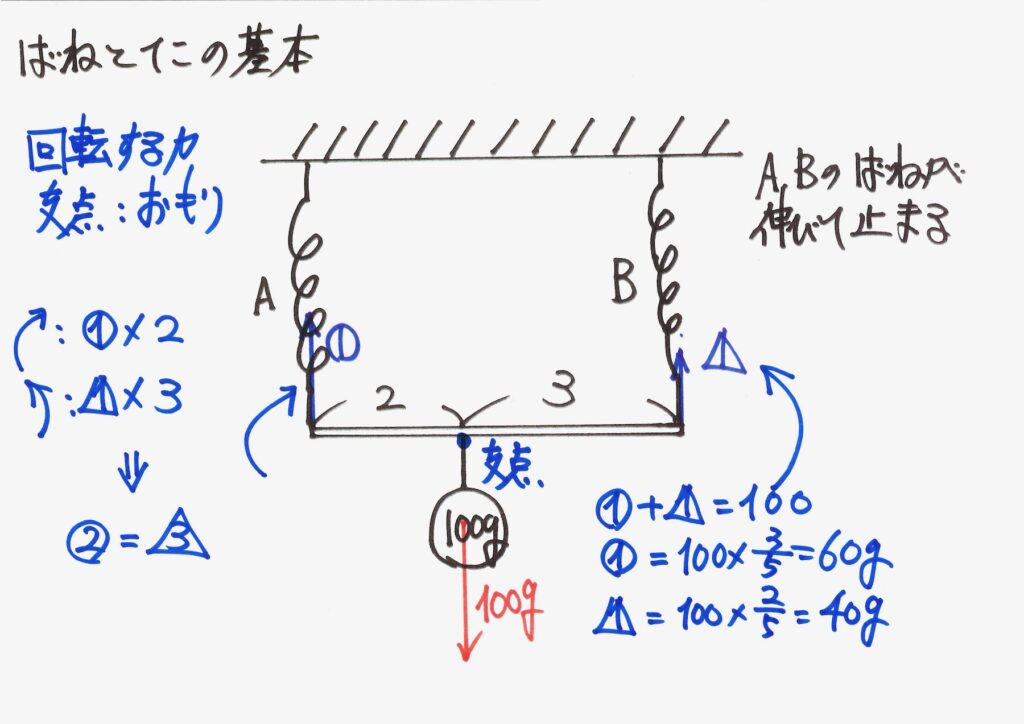
二つの現象・状況は「異なる」のですが、「似ている」面もあります。
このように、様々な現象・状況を「別々に学ぶ」のではなく「共通点を理解する」と良いでしょう。
しっかり理解していれば、「覚えなければならない公式」は少なくなるのです。
生物などは「覚えなければならない」ことが多いですが、自分なりに理解して習得しましょう。
次回は、異なる視点から、この問題を考えます。
次回は下記リンクです。
