前回は「てこのつり合いのコツ・考え方 1〜つり合いと回転する力=モーメント・「つり合い」をイメージ・バネの役割・芥川龍之介「蜘蛛の糸」との比較・「つり合い」とバランス〜」の話でした。
つり合いのイメージ：「てこ」とてんびん算
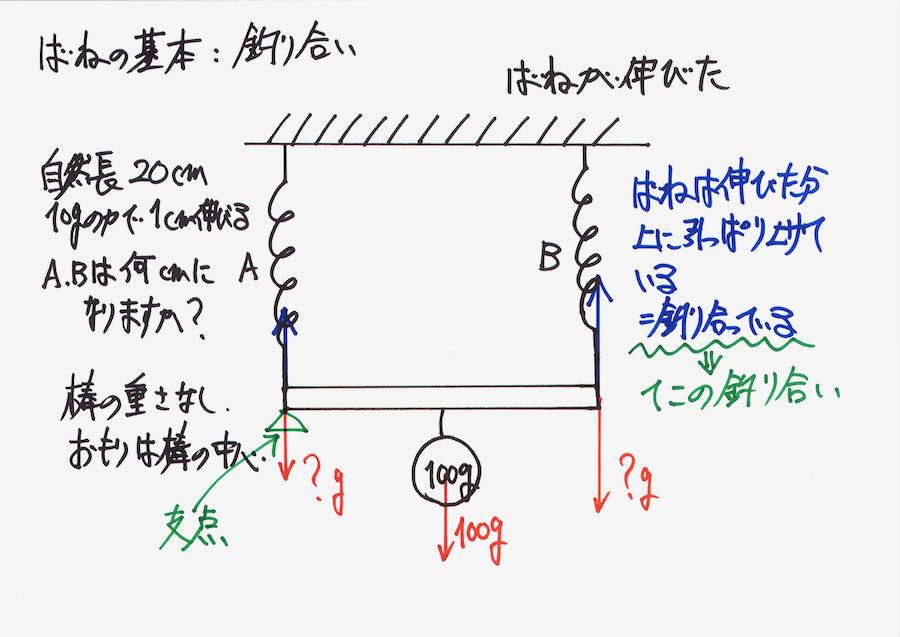
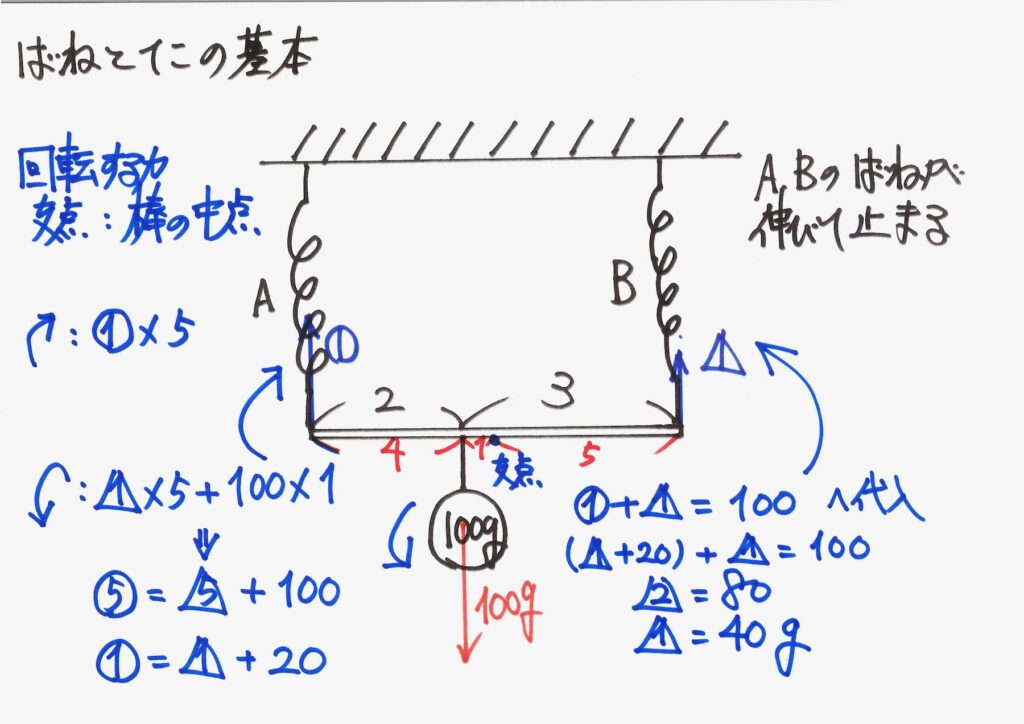
二本の並列バネと一つのおもりがある状況を考えてみましょう。
・バネの直列：そのバネの下にある、おもりの重さの合計の重さがかかる
・バネの並列：そのバネの下にある、おもりの重さの合計を分けた重さがかかる
電池・電流、バネなどで「直列と並列」が登場すると、
男子小学生直列の場合は、
〜のように考えて・・・
女子小学生合成抵抗を
計算して・・・
パターン化する考え方もありますが、いずれの場合も「直列・並列のイメージ」を考えましょう。
てこで考える「モーメント」は、「力 x 長さ」です。
・モーメントは「回転する力」
・「力 x 長さ」でグルッと、何かを回転させるイメージ
そして、「つり合っている」とは、「どこでもつり合っている」ことになります。
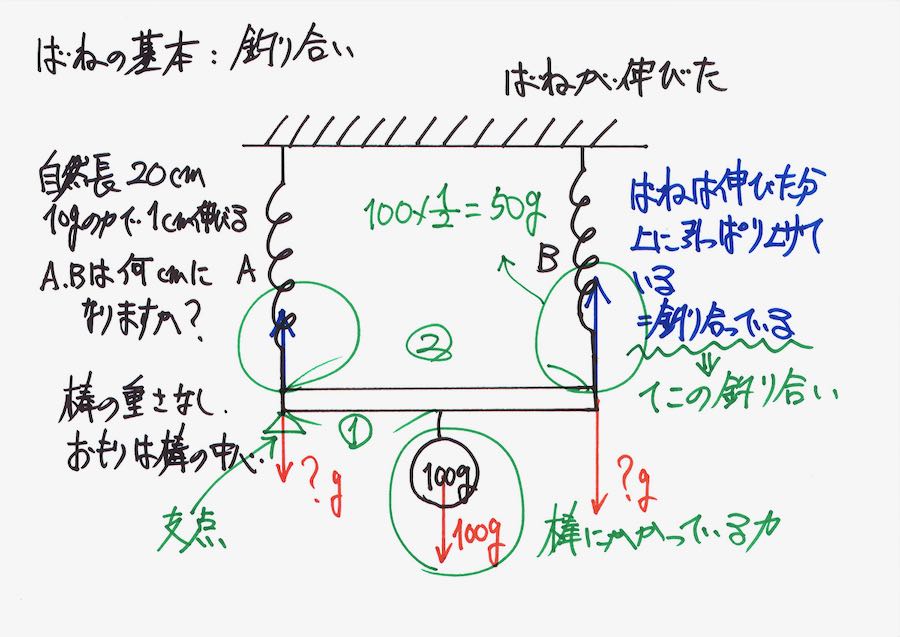
棒の左端の点が「つり合っている」ならば、「その点に回転する力（モーメント）」は0となります。
そして、計算すると「力 x 長さ」が等しいことになるので、
てこの問題を解く際に、大事な「力は長さの逆比」の性質のイメージも理解しましょう。
男子小学生力は、
長さの逆比になるね！
女子小学生バネは重さで
引っ張られるね。
バネとてこは「バネが伸びて、つり合った状態」をイメージすることが大事です。
・「力は、長さの逆比」
・その理由は「回転する力（モーメント）=力 x 長さ」が等しいから
てこの問題は、多くは「てんびんの問題」になります。
てんびん算として、算数で非常に役立つ考え方の「てんびん算」。（上記リンク）
食塩水の問題は、てんびん算、面積算、未知数（①）を設定して方程式的に解く方法があります。
どの解き方でも出来れば良いのですが、てんびん算の考え方を最もお勧めします。
まず、未知数を設定する方程式の（代数的）解き方は、大抵の問題に対処できる応用性の高い解法です。
そのため、「非常に強い武器」になりますが少し「機械的発想」になります。
「方程式の発想」は、中学生〜高校生の時に「数学で学ぶ」姿勢が良いでしょう。
また、面積算も非常に大事な考え方です。
「二つの図形があって、片方の辺を短くして・・・」という算数の問題があります。
こういう問題は、問題の設定通り図形を描いて、解くのが良いでしょう。
食塩水の問題を面積算で考えるより、「てんびん算」をお勧めするのは、「より本質的」だからです。
理科実験などで「上皿てんびん」を使ったことがあるでしょうから、イメージが湧きやすいです。
もう一つ、算数で「てんびん算」をお勧めする大きな理由があります。
それは、「算数と理科を同時に学び、強化できる」ことです。
てこもてんびん算も難しくはなく、「しっかり理解できれば、比較的解けるようになる」分野です。
「てこ」を「公式から」ではなく「イメージをしっかり持って理解」して、
女子小学生てこ・食塩水（てんびん算）の問題は、
少し難しくても、だいたい出来る！
「出来る」という自信が持てるようになりましょう。
てことは何か？
今回は、てこ・てんびんを、しっかりとイメージ・理解しましょう。
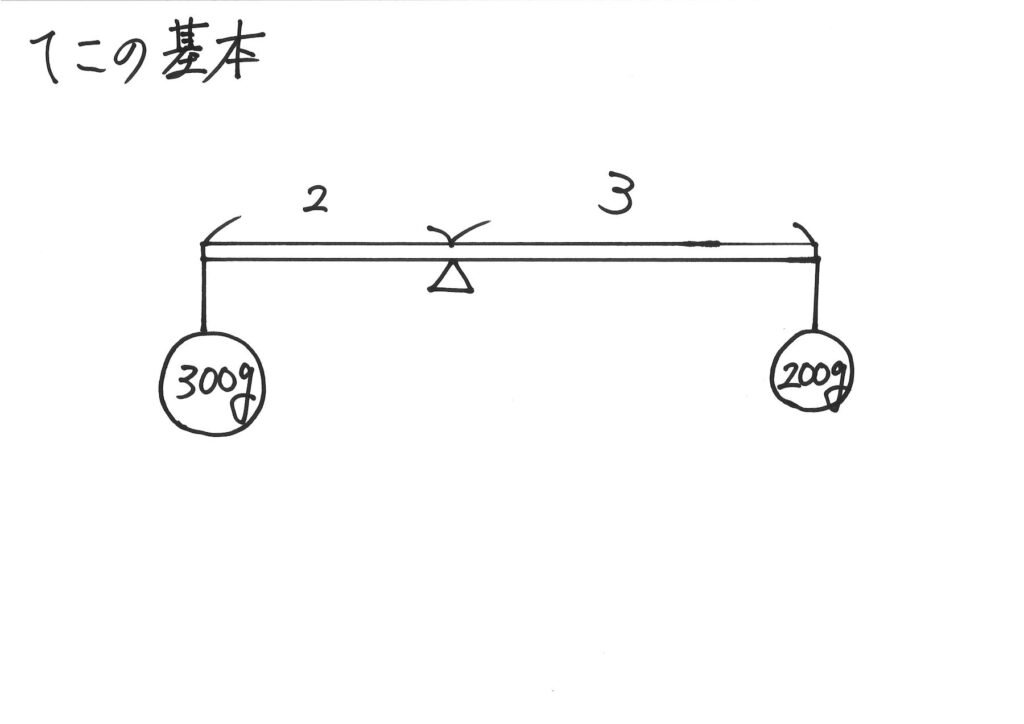
「てこの基本」を考えてみましょう。
上記のような基本モデルに対して、
塾講師おもさ（力）が、
長さの逆比だから・・・
「逆比」と教わった人も多いでしょう。
てんびんは、てこの一つの特殊な状況です。
そもそも、てこ（てんびん）とは何でしょうか？
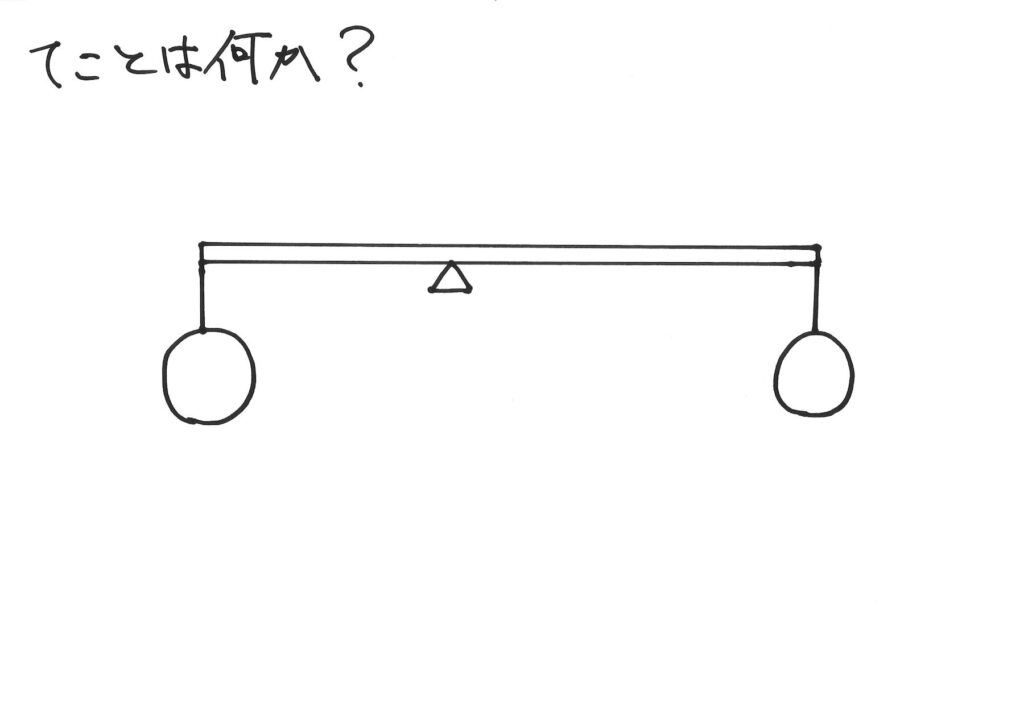
男子小学生てことは何か？って、
考えたことないけど。
男子小学生棒とおもりが
あること、かな？
女子小学生そうね。
「つり合うこと」かな？
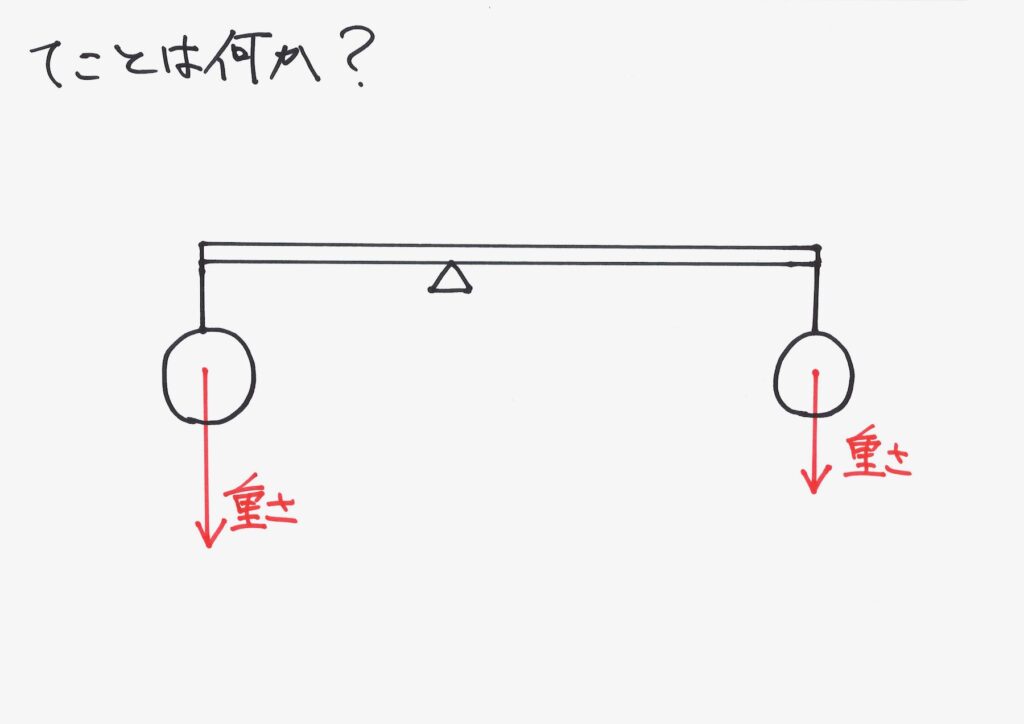
てこに引っ掛かっている、おもりには「重さ」が掛かります。
これまでは、重さと力を考えれば良かったのです。
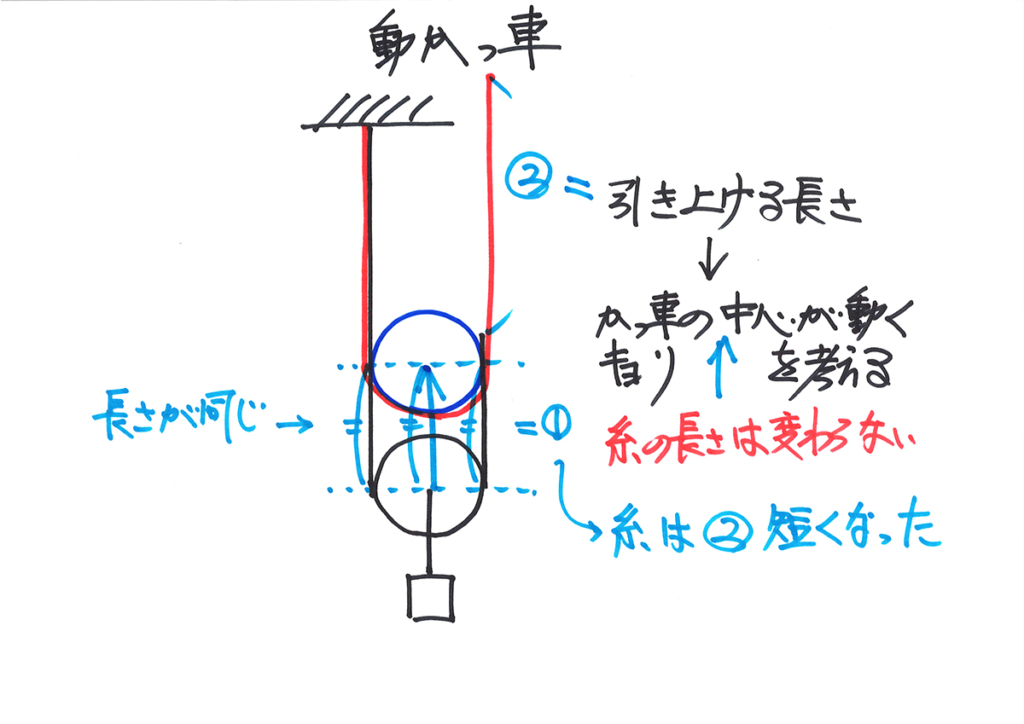
ばねもかっ車も「力」を考えれば解けました。
てこでは「新たな力（モーメント）」が登場します。
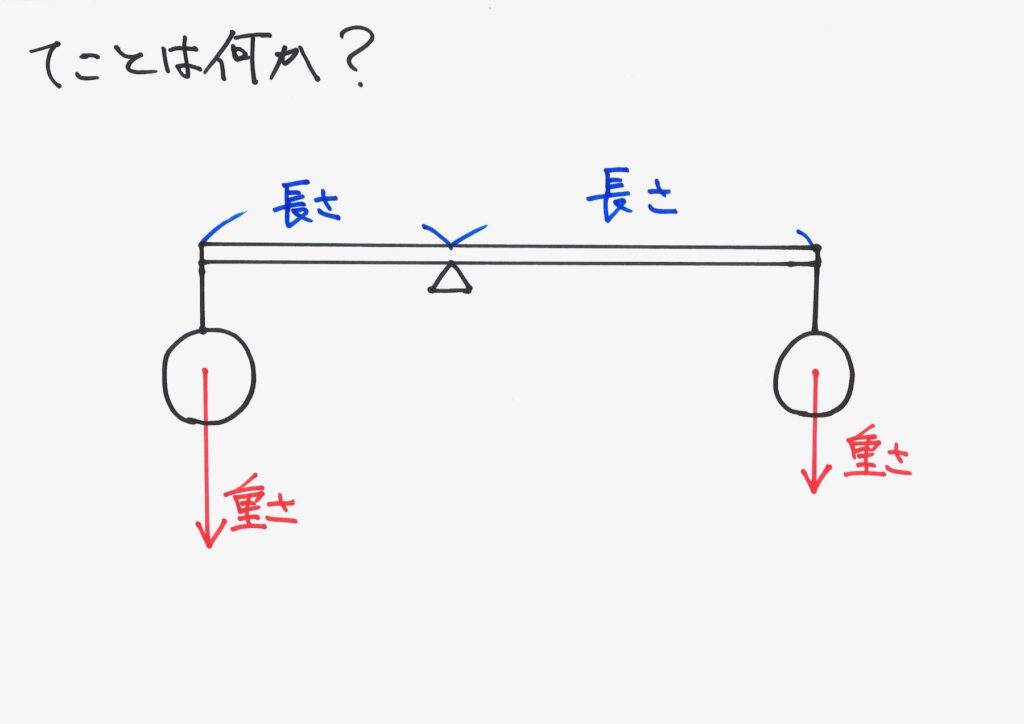
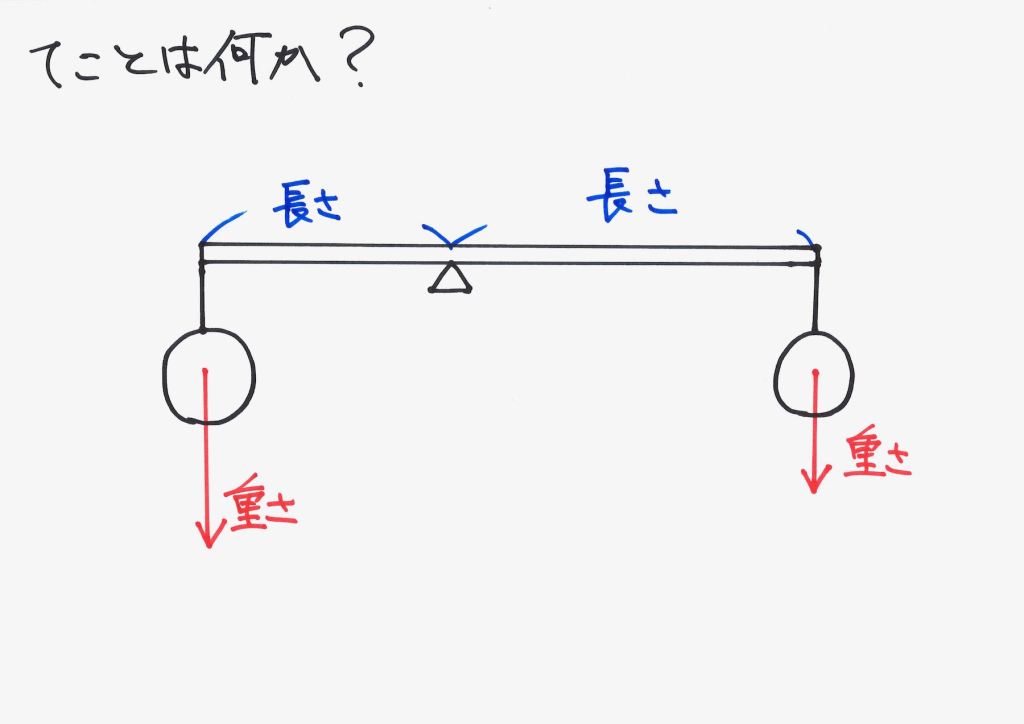
「重さ」だけではなく、「おもりがどの位置にあるか」「おもりと視点の距離」が重要になります。
男子小学生そうだよね。
それで「長さx 重さ」だよね。
その時に、「長さx 重さ」の力がかかるイメージを、しっかり持ちましょう。
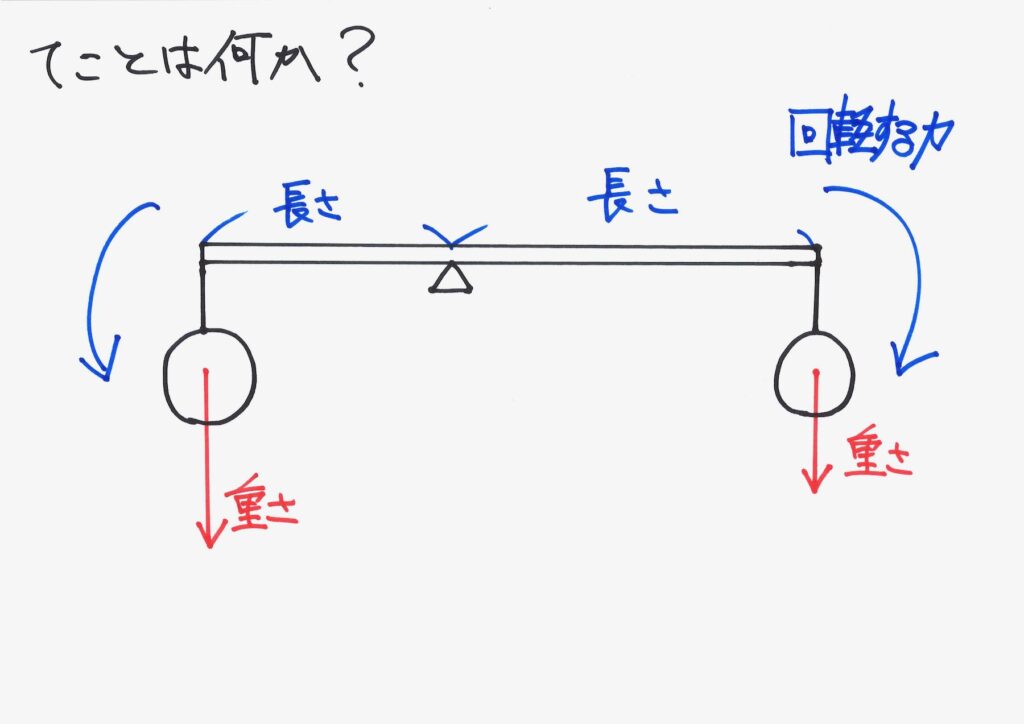
支点の両側にある、おもりは、グルッと回転させる働きをします。
これまでは、おもりは「下向き（重力）に重さをかける」だけでしたが、違う働きです。
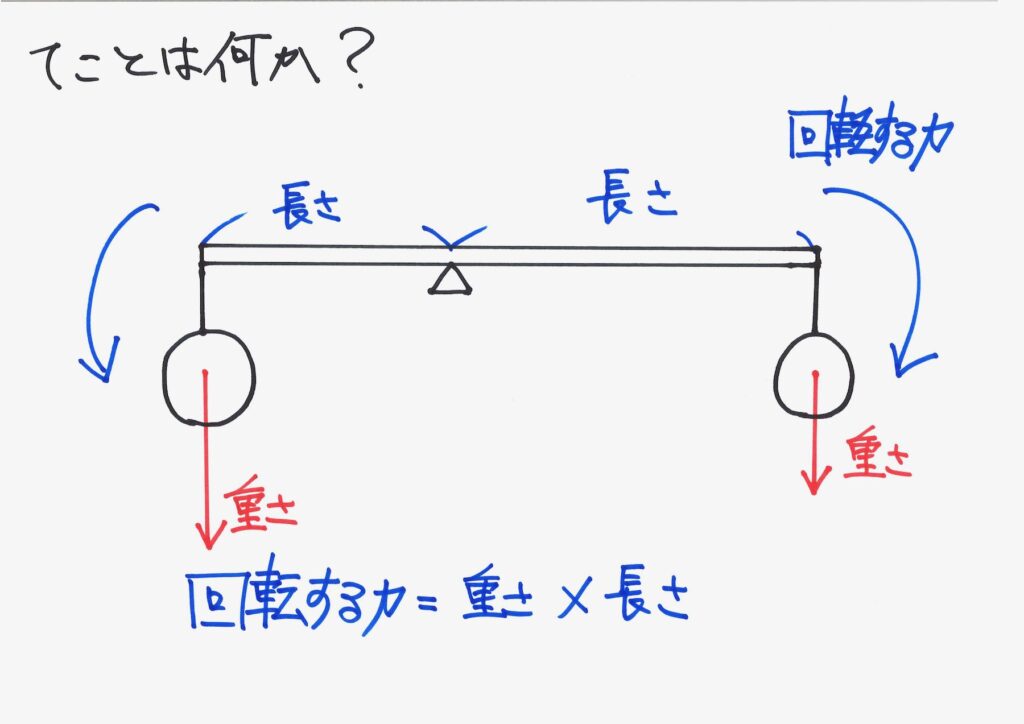
この「重さx長さ」の働きを「モーメント」と呼びます。
この名前は、難しいようでしたら、イメージとして、「回転する力」と考えましょう。
「長さx 重さ」は「力」ではないのですが、イメージとしては「回転をもたらす力」で良いでしょう。
「つり合う」は「普通ではないこと」
理科の問題で、てこ・てんびんが出てくる時は、大抵が「つり合っている」状況です。
男子小学生確かに
そうだね。
女子小学生「釣り合ってません」という問題は、
ないね・・・
問題の設定で「一時的につり合わなくなる」状況があるかもしれません。
その場合も、最終的には「つり合った」状態になるでしょう。
学校の理科実験で、「分銅を使って、てんびんの釣り合いをとる」実験をしたことがあると思います。
男子小学生僕も
やったよ！
男子小学生あれ、
結構難しいんだ。
女子小学生そうよね。
少しずつ乗せるのが大事だね・・・
女子小学生ちょっと分銅おくと、
つり合わなくなったりするね・・・
「分銅を置いて、つり合う」という実験は、意外と難しいです。
中学以上では電子質量計が登場するので、なかなかやらないです。
現実には「つり合いをとる」のは、難しいことです。
つまり、「つり合う」ことは「普通ではないこと」で「珍しいこと」なのです。
「つり合わない」のが「普通」なのです。
「回転する力」をグルッと描いてみて、「釣り合うこと」をイメージしてみましょう。
次回は下記リンクです。
