前回は「ばねの伸びの考え方 3〜並列・おもり1個・バネと電池・力のつり合い・対称性・折り返して同じ〜」の話でした。
バネの役割：「蜘蛛の糸」との比較
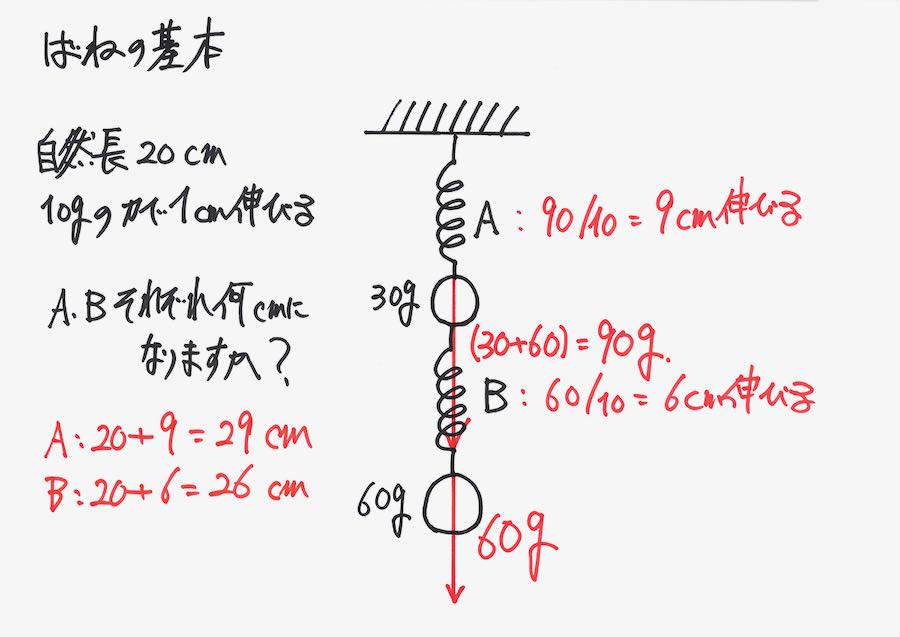
バネの直列・並列つなぎの時、それぞれのバネに「かかる重さ」を考えました。
・バネの直列：そのバネの下にある、おもりの重さの合計の重さがかかる
・バネの並列：そのバネの下にある、おもりの重さの合計を分けた重さがかかる
バネの直列と並列で大きく異なるのは、直列は「下の重さを全て」負担し、並列は「分けて」負担します。
感覚的には、「重さを分けて負担する」並列の方が「バネが仲良し」のイメージです。
芥川龍之介の「蜘蛛の糸」を、読んだことがある方がいらっしゃるでしょう。
非常に短い短編小説ですが、極めて多くのコトが詰まっている「蜘蛛の糸」。
読んだことがない方は、短い時間で読め、国語対策にもなるので、読んでみましょう。
この時、罪人のカンダタが登る「蜘蛛の糸」が一本でした。
そして、カンダタ含め大勢の方（罪人）が、「直列になってぶら下がった」のが問題でした。
やむ得ない状況ですが、大勢の方が「並列になってぶら下がった」ら、脱出できたかもしれません。
バネの直列は、「特に上のバネが大変な立場」というイメージを持ちましょう。
確かに、
上のバネは、沢山の重さがかかるね・・・
それでも
頑張っているのが、バネなんだね。
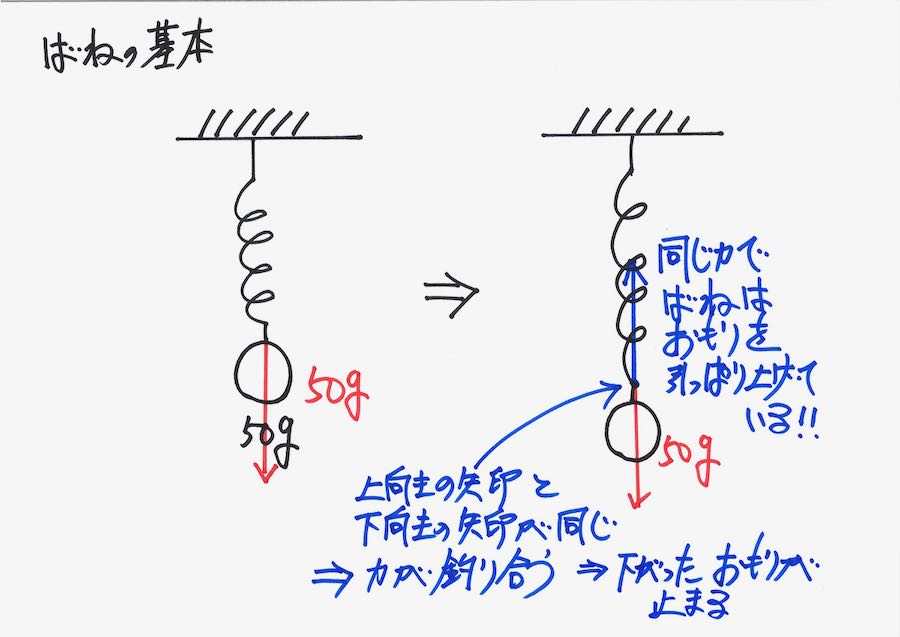
バネは「引っ張られる」だけではなく、おもり・重さを「引っ張り上げている」のです。
「バネが途中で切れてしまう」設定の問題はなさそうです。
現実問題としては、「かかる重さが大きいと、バネが切れてしまう」可能性はあります。
直列・並列のいずれの場合も、「バネの役割」をしっかり理解しておきましょう。
つり合いと回転する力（モーメント）
今回からは、てこの話もします。
てこは、
知ってるよ。
モーメントを
考えるんだよね。
中学生以上は、「長さ x 力」を「モーメント」で理解します。
小学生は、「モーメント」が難しく感じないようでしたら、モーメントで良いでしょう。
なんだか、
難しそうで、馴染めない・・・
という方もいらっしゃるでしょうから、その場合は「回転する力」とイメージしましょう。
・モーメントは「回転する力」
・「力 x 長さ」でグルッと、何かを回転させるイメージ
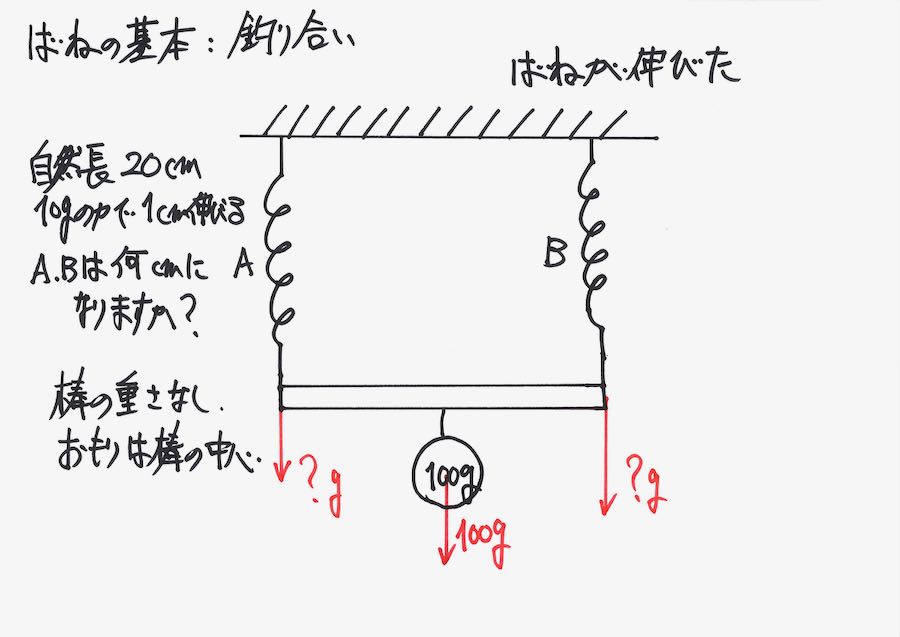
前回の問題を考えましょう。
この問題は、おもりが「棒の中心にある」から「対称性」を考えて、解けました。
おもりの位置が少し寄って、たとえば「棒を2 : 3」に分割する点に、おもりがある場合もあります。
その場合は、
知ってるよ。
棒の長さの比の
「逆比の重さ」が、かかるよね。
この「長さの逆比の重さ」は「公式」として暗記しておく内容ですが、理解しておきましょう。
支点を考える：「つり合い」をイメージ
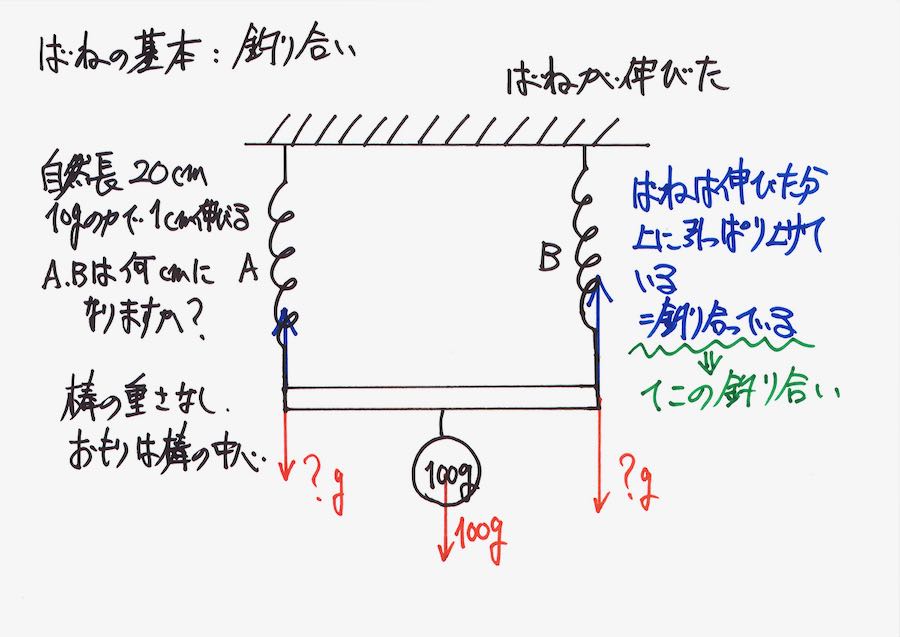
今回は、この問題で「応用問題の基礎」を考えてゆきましょう。
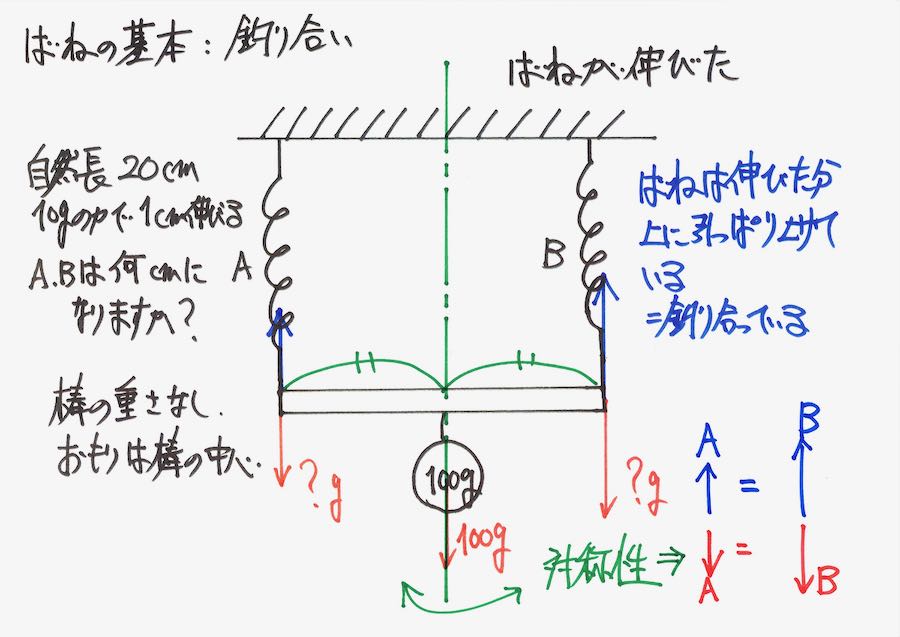
バネが伸びて、おもりを支えて「力が釣り合っている」状況です。
この「力が釣り合っている」のは、「棒がてこ」であると考えても「釣り合っている」はずです。
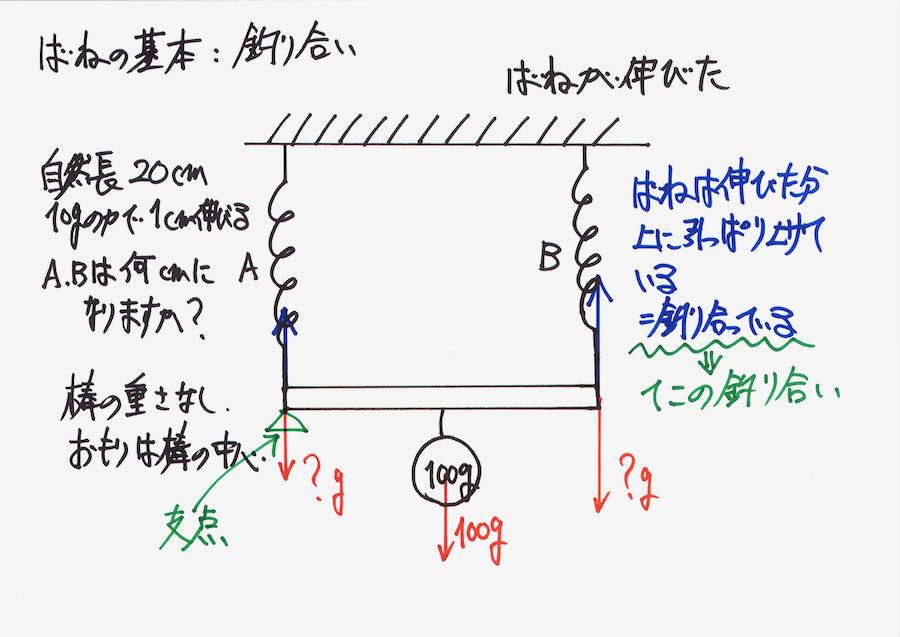
例えば、バネAと棒のつながっている部分（接点）を、支点と考えましょう。
でも、
支点はないでしょ・・・
ないのに、
「ある」と考えて良いの？
支点は「ない」のですが、「釣り合っている」状況を考える「仮想的支点」と考えて下さい。
「仮想的」って
難しいよ・・・
「仮想的」というと難しく感じるかもしれませんが、「イメージ」です。
例えば、「支点」あるいは「釣り合いが取れている点」と考えてみましょう。
「新たに実物の支点」を加えると、状況が変わってしまうので、そうではありません。
ここで、バネは「おもりで引っ張られる」ではなく「おもりを引っ張り上げている」イメージです。
「引っ張られる」と「引っ張り上げている」では真逆のイメージですが、「つり合い」をイメージしましょう。
「つり合い」とバランス
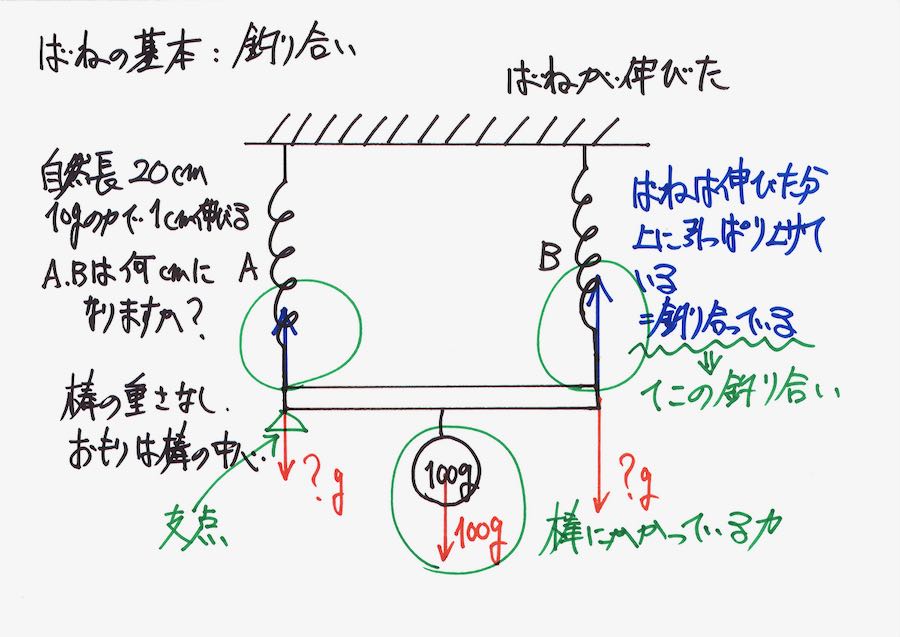
棒には、緑丸で囲った三つの力が、かかっています。
A、Bのバネの下にかかっている赤い矢印は、「おもりの重さを分けた場合」です。
今回は、対称性などで「おもりの重さを分ける」はしないので、赤の矢印は無視しましょう。
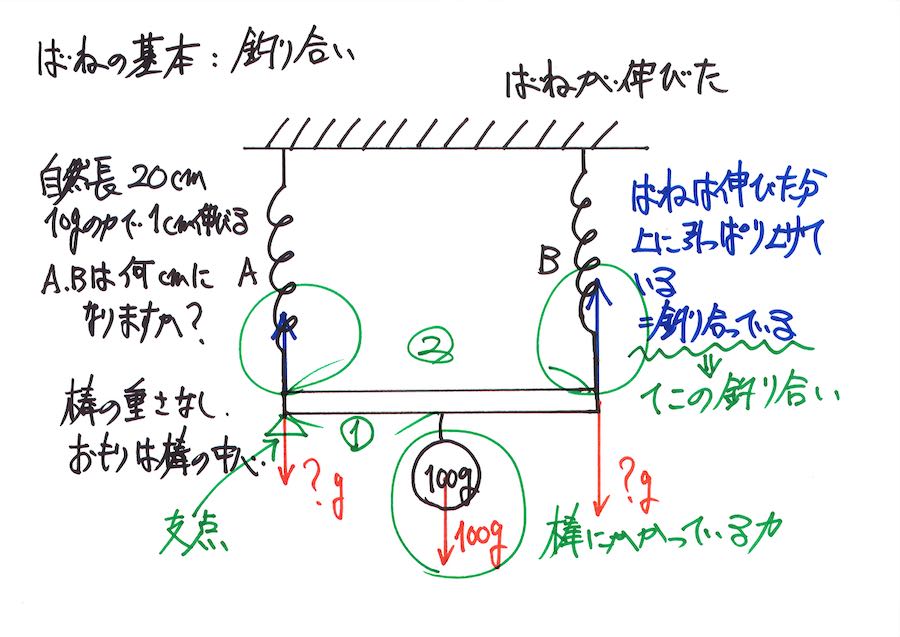
この状況を、てこで考えてみましょう。
支点に対して、バネAが引っ張る力は同じ点なので、「回転する力」の長さが0です。
そこで、「てこの原理」である「回転する力」には関係ないです。
そして、「おもりが棒の中心」にあるので、バネBの力・おもりの重さと支点の距離は2 :1 です。
・グルっと回転する力「力 x 長さ」がつり合う
「回転する力」がつり合う「てこの原理」を考えましょう。
「てこの原理」を考えると、力は 1 : 2になります。
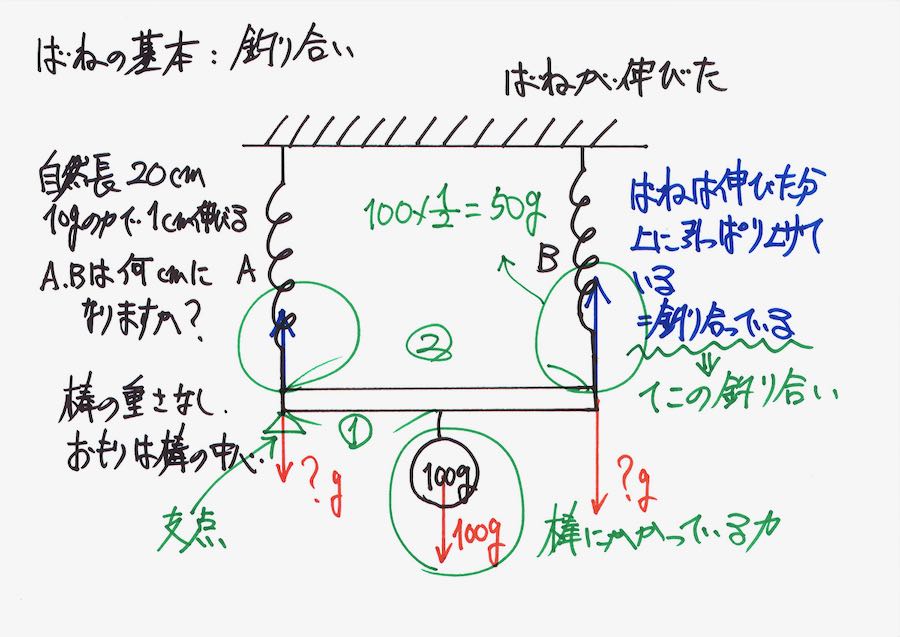
これで、前回と同じ結果になりました。
状況や設定が変わっても、考え方は同じ
本当だ。
確かに同じになる。
この考え方なら、おもりがどこにあっても
分かる！
大事なことに、気づきましたね。
「おもりがどこにあっても分かる」ような考え方が、理科では特に大事です。
「状況や設定が変わっても、考え方は同じ」なのです。
そして、この「てこの原理・考え方」は、算数の「てんびん算」と同じです。
「状況をパターン化して、問題を解く」やり方もあります。
「基本をしっかり理解」していると、「状況が変わっても分かる」のです。
なんだか、
不思議・・・
バネが伸びて「釣り合っている」（物理的）状況は、色々と考えられます。
今回は、「バネAと棒のつながっている部分を、支点」で考えました。
同様に「バネBと棒のつながっている部分を、支点」で考えてみましょう。
他の点でも良いです。
「つり合っている」や「バランスが取れている」のは、どこで考えても同じはずです。
自分で「釣り合っている状況」をイメージしてみましょう。
「釣り合っている」
って大事なんだね！
バネ・てこの話って、
面白い！
理科の現象は、面白いことが多いです。
もっともっと
勉強しなきゃ！
だけではなく、イメージして楽しみましょう。
「イメージして楽しむ」姿勢が「応用力を上げ、学力を上げる」大事なポイントです。
