前回は「ばねの伸びの考え方 2〜直列・おもり2個・基本を重視・伸びる状況を描く・力のつり合い〜」の話でした。
力や電圧を矢印で表現:現象をイメージ
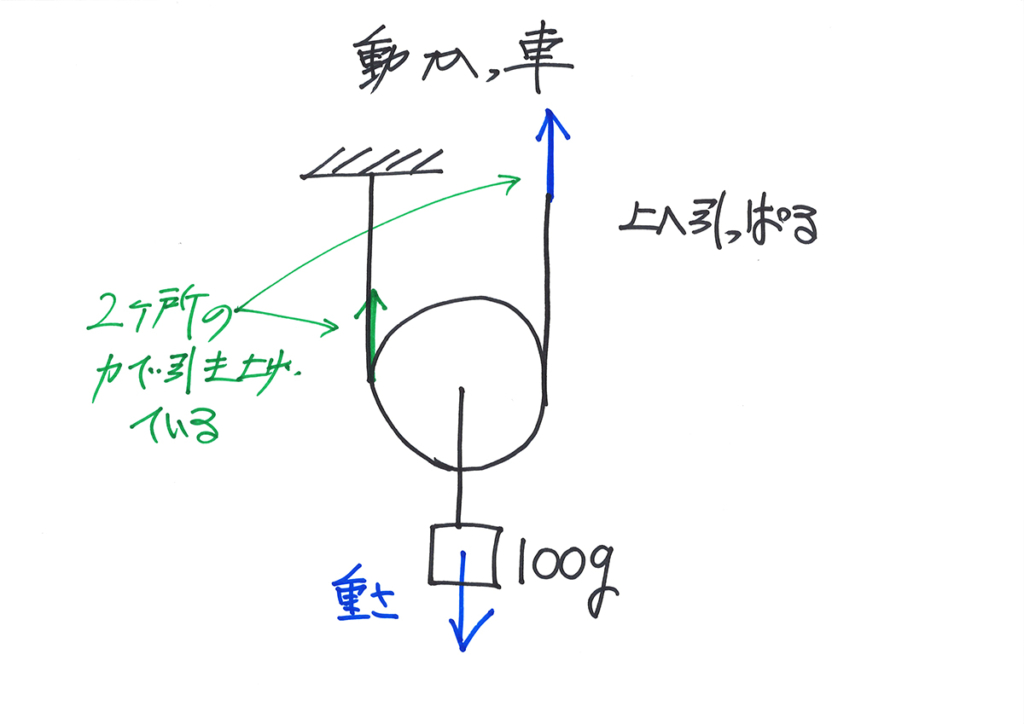
かっ車を考えた時、「おもりの重さ」の矢印と「引っ張り上げる力」の矢印を考えてみましょう。
・向き:力のかかる向き
・長さ:力の大きさ・長さ
矢印の「向き」と「大きさ・長さ」が、「ちょうど同じになる」考え方で、スッキリ理解できます。
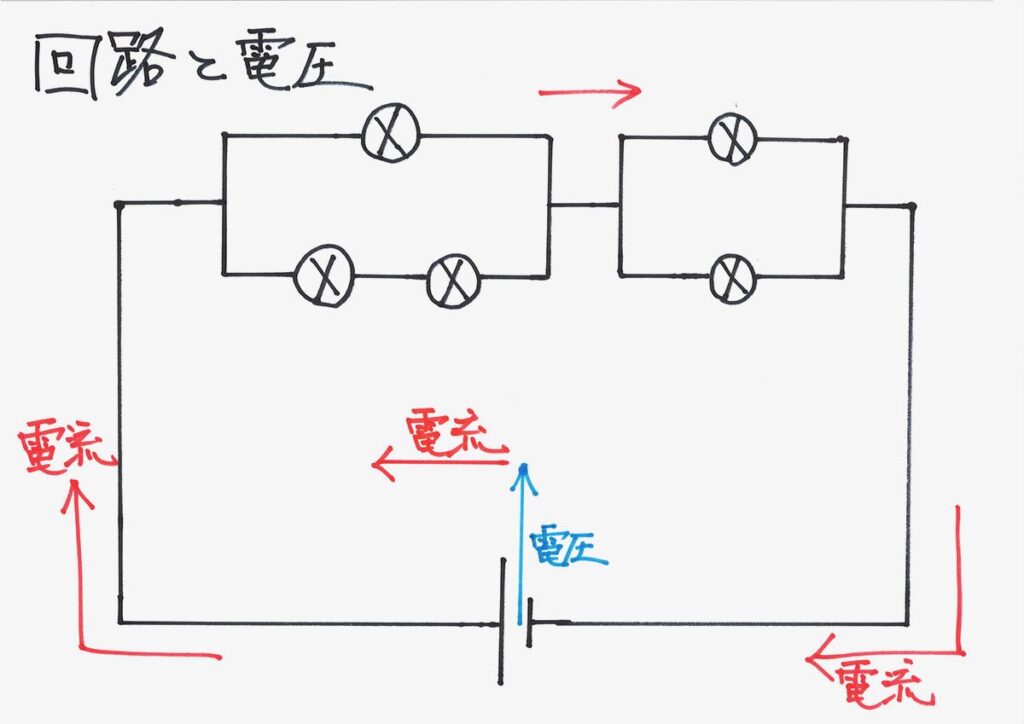
回路の電圧と電流を考えた時も同様に、電圧と電流を矢印で描きました。
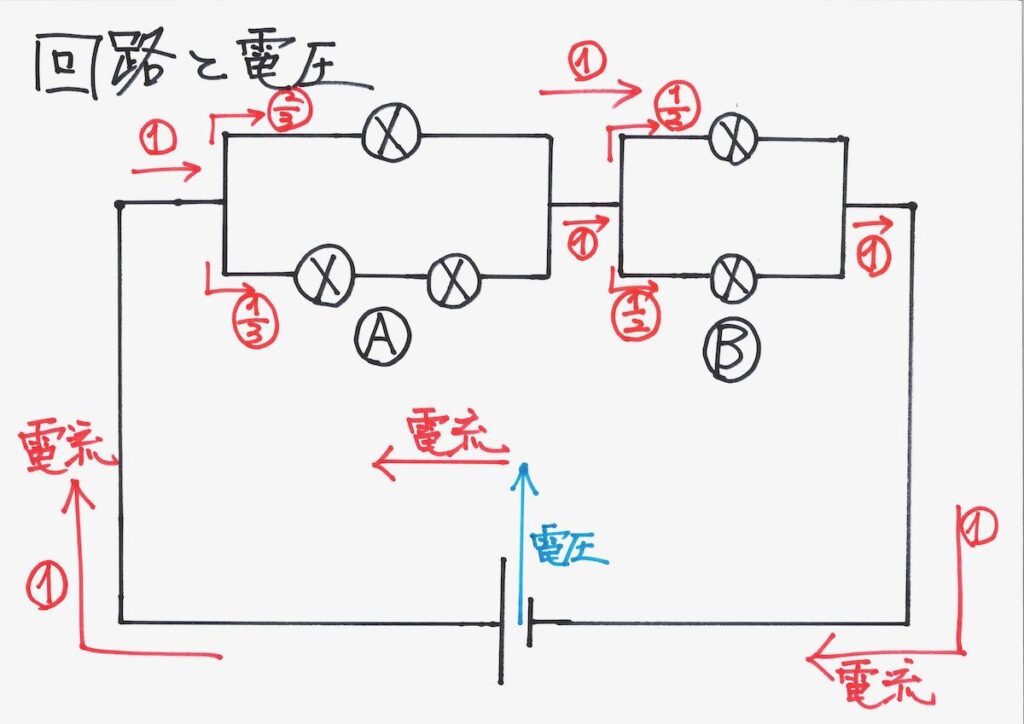
・電池がエイッと電圧を発生させて、電流がグルッと一周するモノ
電池が直列・並列で繋がるとき、電池の数に応じて、電圧の高さが変わる、電池の持ちが変わります。
流れる電流が「分かれる」「合流する」イメージは、自然の川をイメージします。

これらかっ車・電気の分野で、もっと難しい・複雑な問題は沢山あります。
それらの問題も、同じように「働く力や電圧・電流などを矢印で描く」と分かるようになるでしょう。
バネの直列・並列と電池の直列・並列
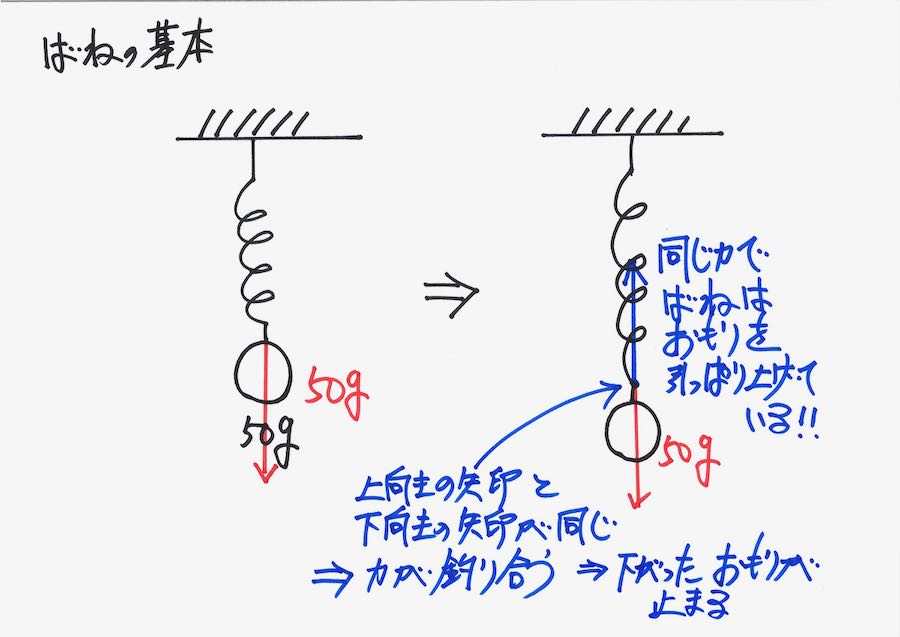
電気の問題と同様に、「直列の場合」と「並列の場合」などに分けて考える場合が多い、バネの問題。
おもりをつけたら「バネが伸びる」のですが、この「伸びる状況」をあまり考えない傾向もあります。
バネが伸びて、「おもりの重さとバネの引っ張る力が釣り合う」イメージが大事です。
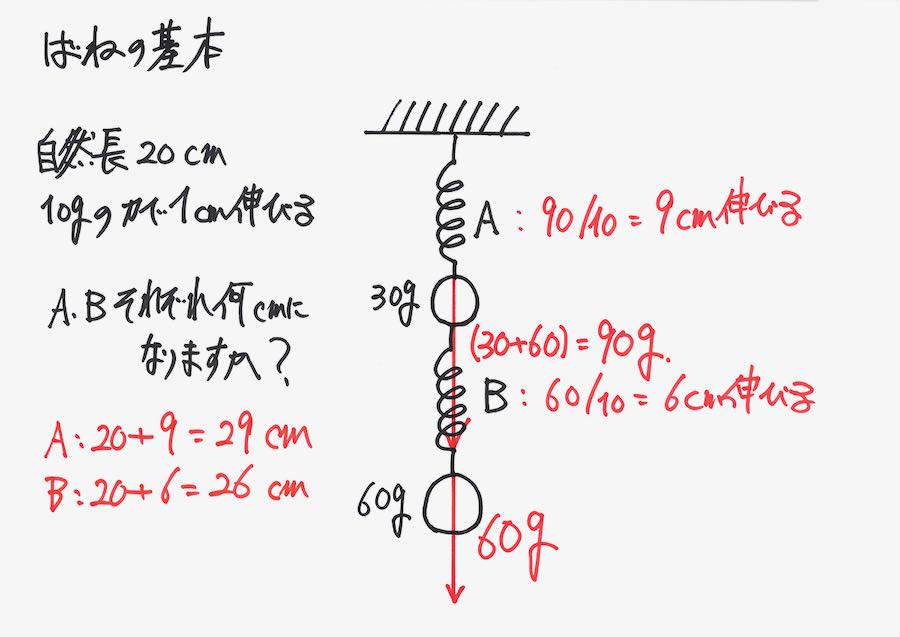
具体的に「バネが伸びて、釣り合う」イメージと、バネが直列につないだ時の力を考えました。
今回は、バネの並列つなぎを考えます。
直列・並列は、他でも考えました。
 男子小学生
男子小学生電気で、電池や電球も
直列・並列ってあったね。



直列と並列は
簡単なんだけど、電池とバネで混乱することがある・・・
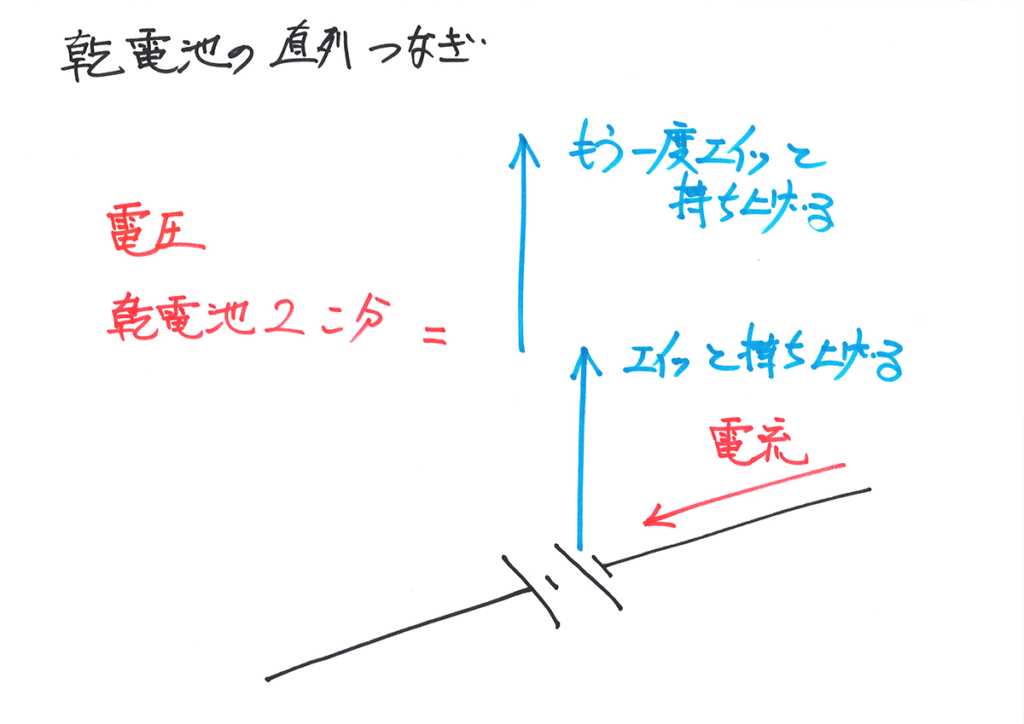

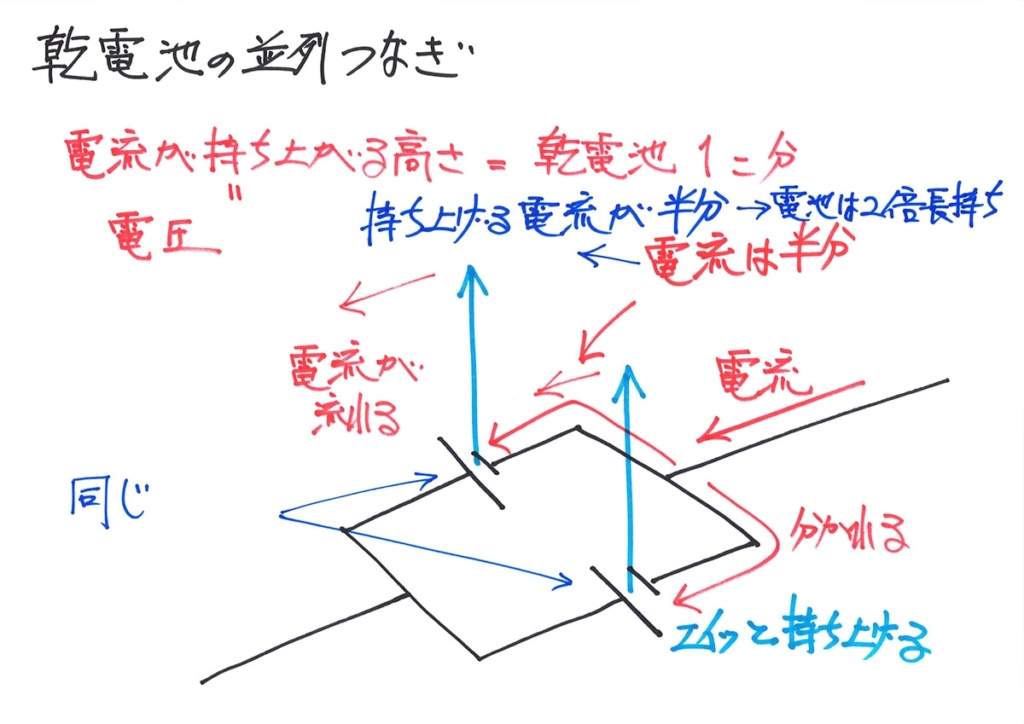

電池の直列つなぎ・並列つなぎに関して、「電池が電流を持ち上げる高さ(電圧)」を矢印で表現しました。
バネの直列つなぎと電池の直列つなぎでは、下記のようになります。
・電池の直列:電池の数の高さの合計(電圧)分、電流が持ち上がる
・バネの直列:あるバネの下にかかっている重さの合計(重さ)分、バネが伸びて釣り合う
内容は異なりますが、「似た部分もある」と考えられます。
バネ・電池などの分野で、それぞれ直列・並列などがありますが「考え方は似ている部分」があります。
これらの分野それぞれに対して、「全部違う」と考えると大変です。
基本的なことを理解して、矢印を描いて考えて、同じように考える姿勢も大事でしょう。
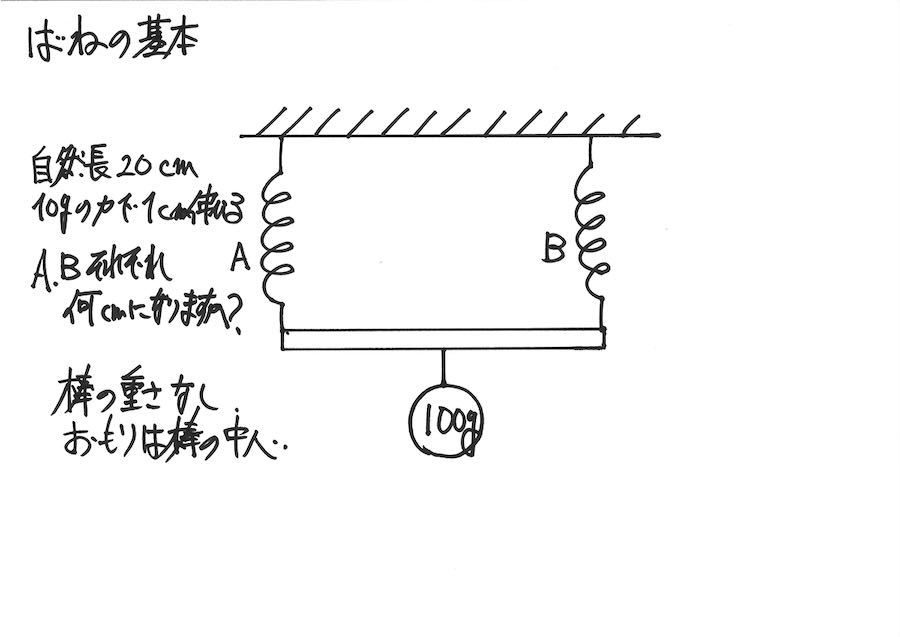

今回は、バネが2本で、おもりと棒(重さのない棒)を支える問題を考えましょう。



これも、
分かるよ。
電気でも、バネでも理科は「状況をしっかり考える」ようにしましょう。
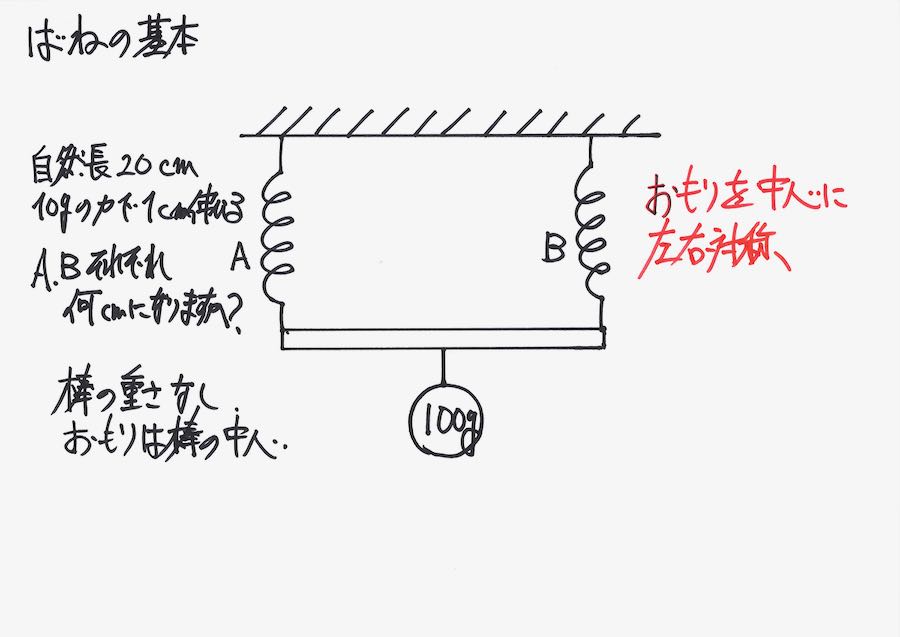

おもりを中心に左右対称です。
おもりの重さを矢印で描いて、「力がかかっているイメージ」を持ちましょう。
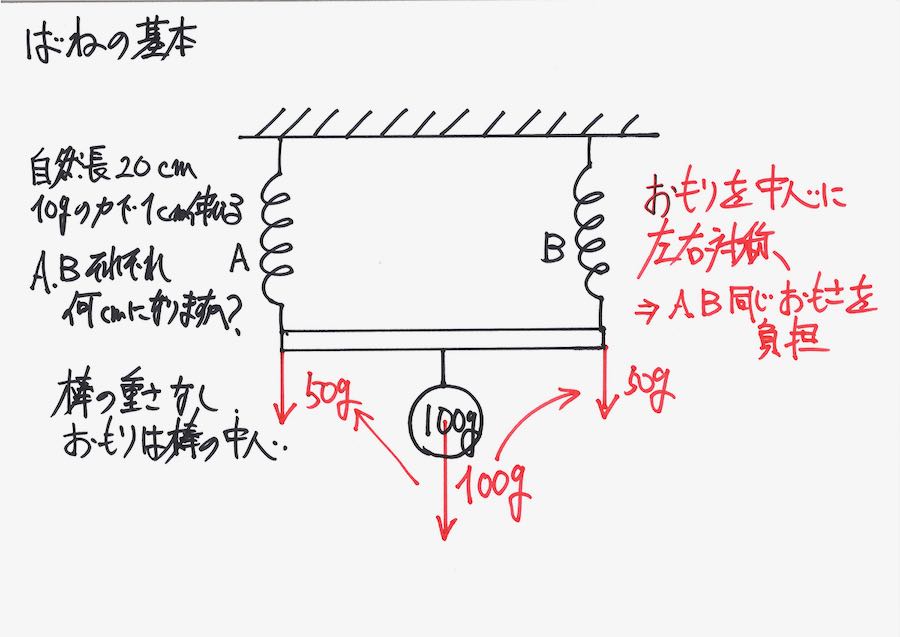

左右対称なので、100gのおもりの重さを「A,Bのバネで同じ重さを負担」します。
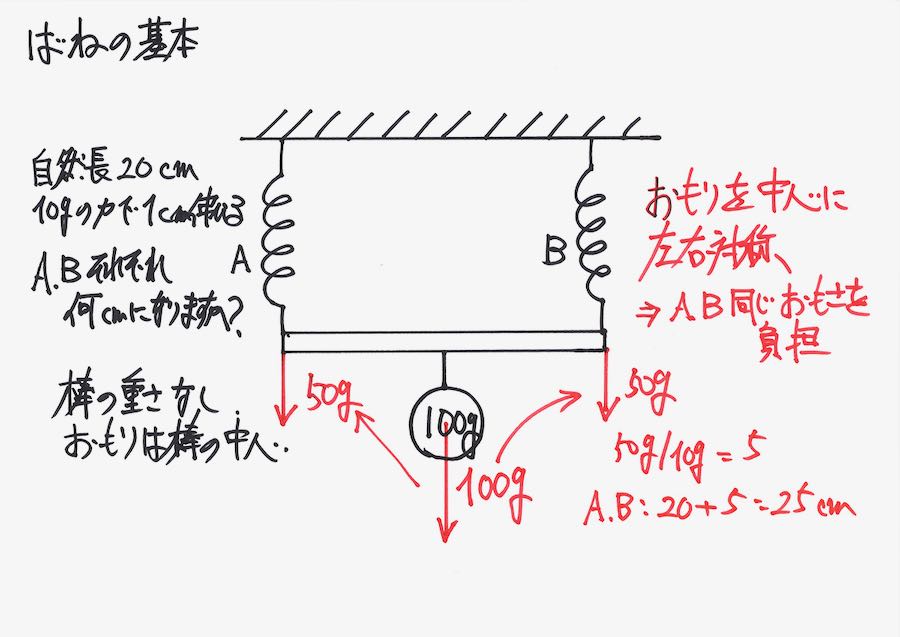

すると、それぞれ50gの重さがかかる分バネが伸びます。



これは、すんなり
分かるよ!



おもりの位置が真ん中でなかったら、
「長さの逆比」でバネが伸びるよ!
「長さの逆比」に関しては、今度考えることにします。
バネの並列つなぎは、このように「おもりの重さが並列のバネにどうかかるか」を考えれば出来ます。
この点では、直列でも並列でも、同じように「どのバネにどのくらいの重さがかかるか」が大事です。



確かに直列の場合、並列の場合で分けて
考えるよりも・・・



どのバネにどのくらいの重さがかかるか、を
考えた方が良いかも・・・
バネに「どのように・どのくらいの重さがかかるか」を、重さの矢印を描いて理解しましょう。
バネと力のつり合いをイメージ:対称性=折り返して同じ


前回考えた、バネの基本を考えて「バネが伸びて、力が釣り合った」絵を描きましょう。
バネが少し伸びた絵を「グルグルっと描いてみる」ようにしましょう。
こういう絵は「見れば当たり前」ですが、描いてみるとイメージ出来るようになります。
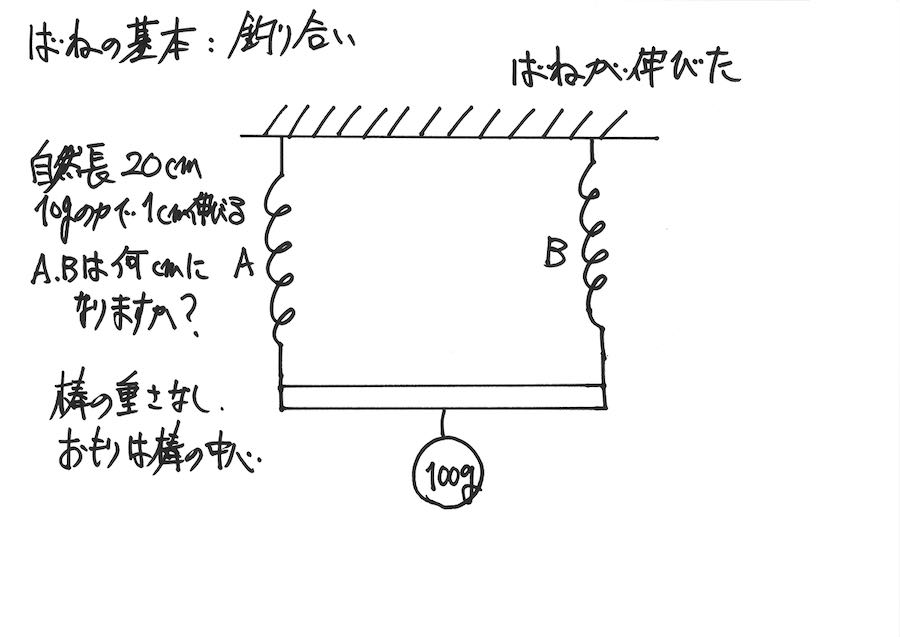

伸びたバネには、それぞれ同じ重さがかかりますが、「同じであることが、分からない」とします。
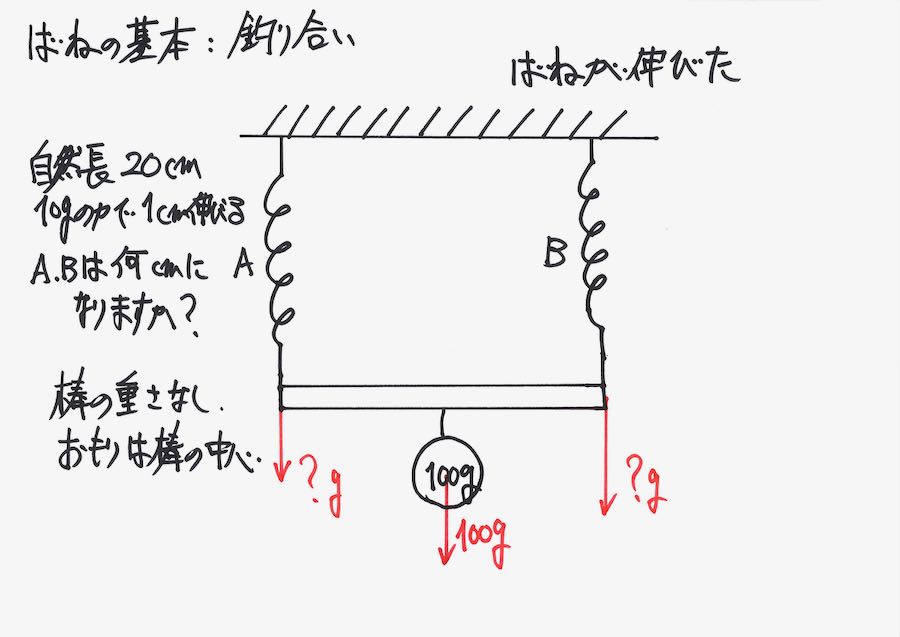

A,Bのバネにそれぞれ、「どのくらいの重さがかかるか」が不明のまま、考えましょう。
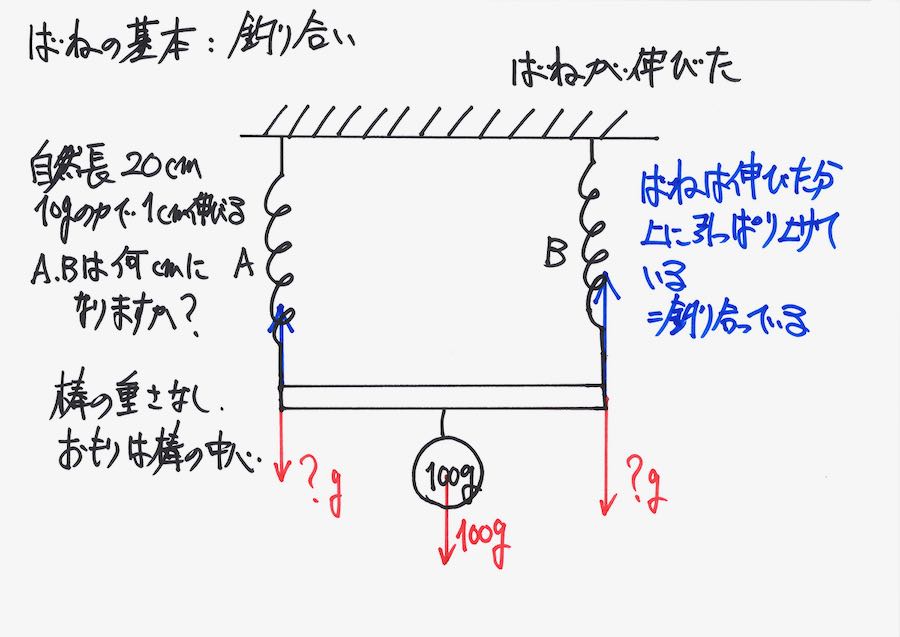

それぞれのバネは、「かかる重さと同じ力で引っ張り上げて、釣り合う」状態になります。
ここで、状況を考えてみましょう。
大事なことは「おもりの左右で対称性がある」ことです。
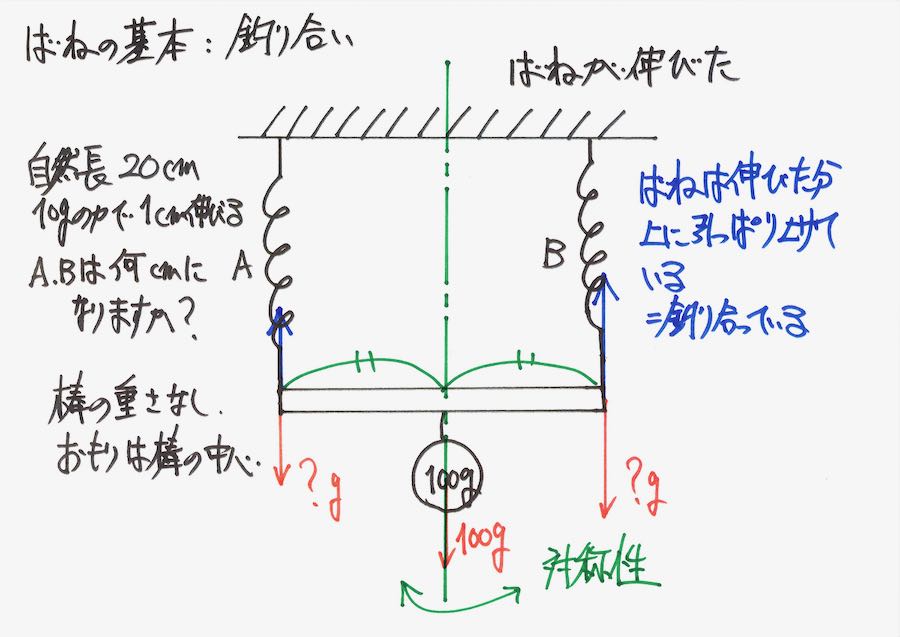

「左右で同じ」はずですから、他にも「同じこと」があるはずです。
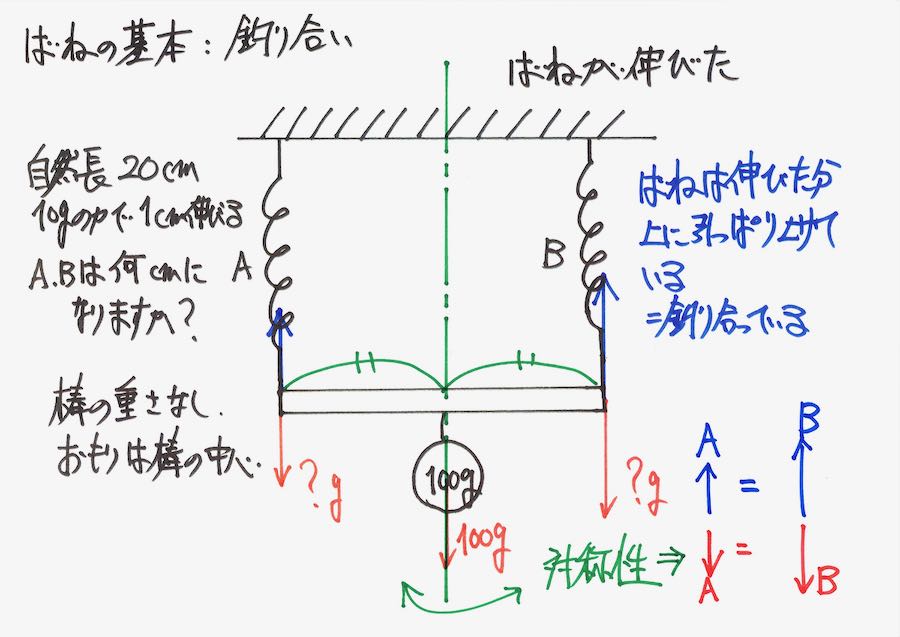

A,Bそれぞれの重さ、そして、バネが引っ張り上げる力も同じ、と分かります。
対称性は、算数・理科で非常に大事な性質です。
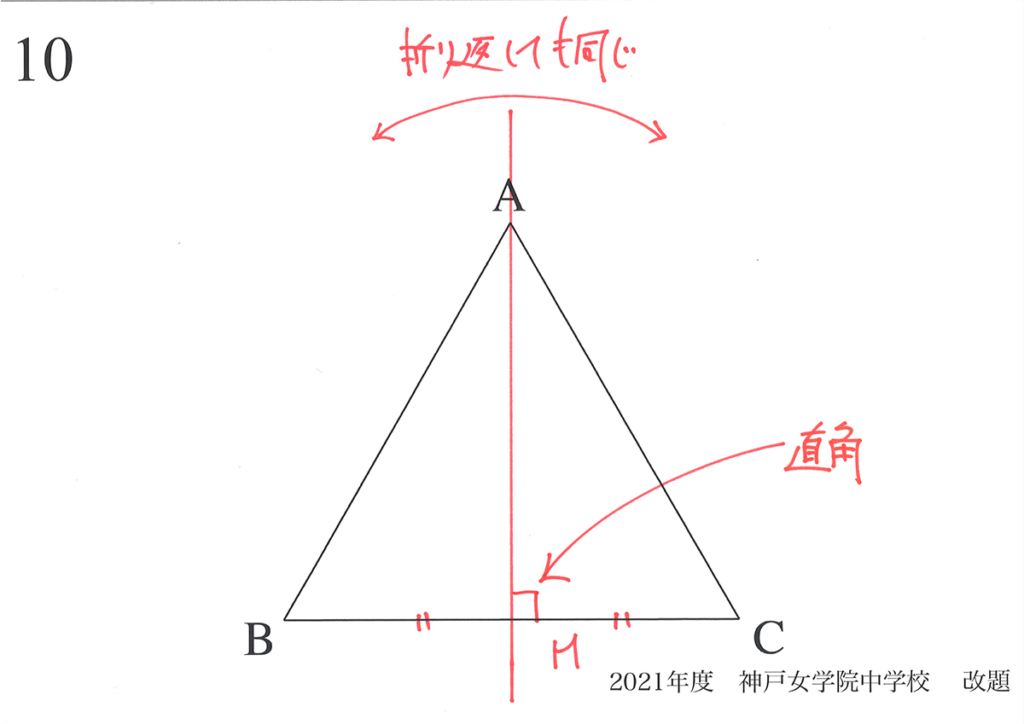

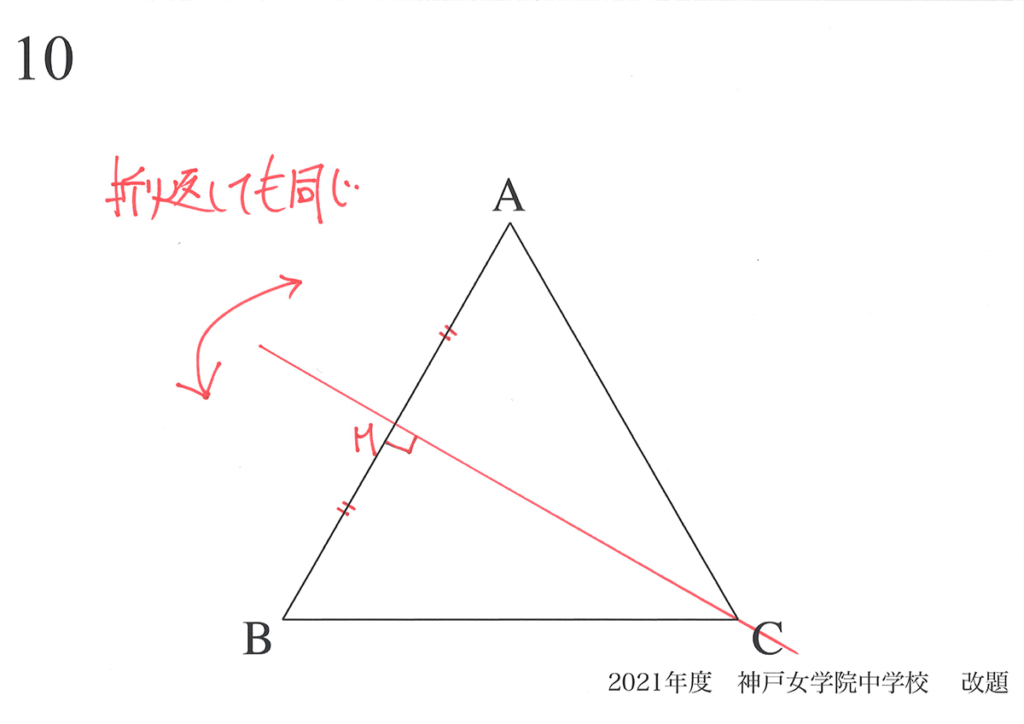

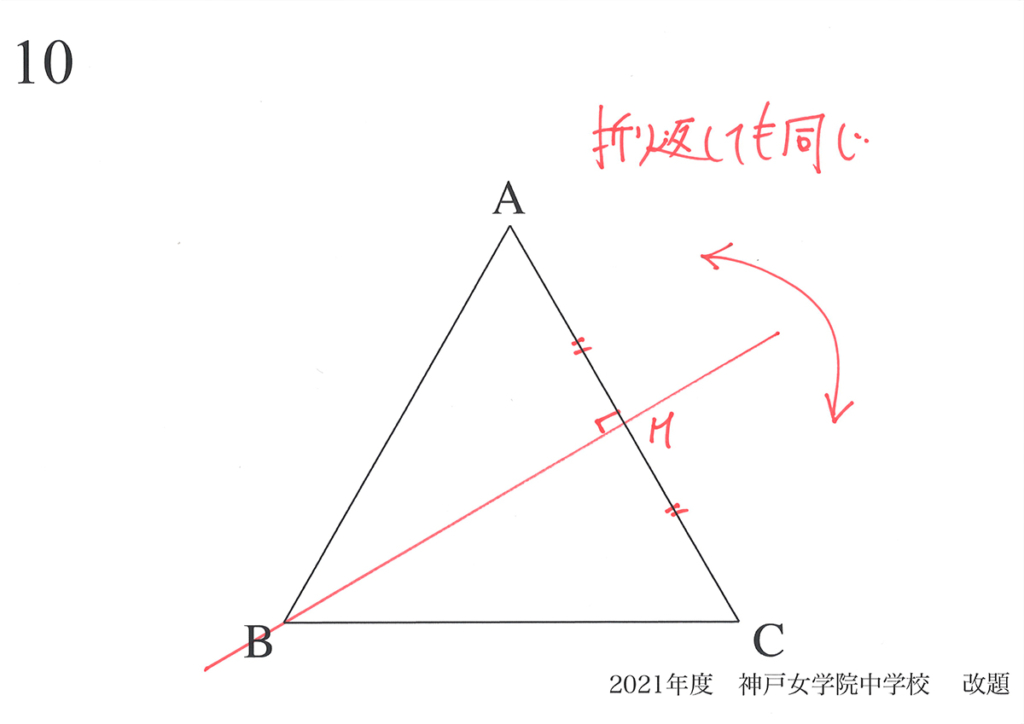

「対称性」というと難しく感じるかもしれませんが、「折り返して同じ」と考えましょう。
上のように「つり合いを考える」のは、少し遠回りな考え方かもしれません。



「つり合う」って考えなくても、
「引っ張られる」でも同じ答えだね。



答えが同じだったら、今まで通り、
「引っ張られる」でも良いかも・・・



「つり合う」と考えるのは、
バネとおもりが止まるイメージだね。
・おもりなどの「モノ」にかかる力がつり合って、止まる(静止する)状況
バネ・かっ車などでは、おもりなどがの「力・重さ」が掛かって、つり合います。
この時、「つり合って止まる」のを「静止状態」と言います。
「バネが伸びて、力が釣り合う」イメージをしっかり持つと、応用問題も解けます。
次回は、この問題を「てこの考え方」で考えてみましょう。
次回は下記リンクです。


