秒速で考える「速さ」の具体的イメージ〜だいたいの計算の考え方「桁を合わせる・近づける」・「だいたいの感覚」とテストの◯✖️・「考える自由」を持つ〜｜日常生活と理科・速さの話2

前回は「「歩く速さ」と「走る速さ」の具体的なイメージ〜「電車の速さ」と比較・電車の動きを観察・「だいたい」が大事な理科の現象のイメージ〜」の話でした。

秒速で考える「速さ」の具体的イメージ

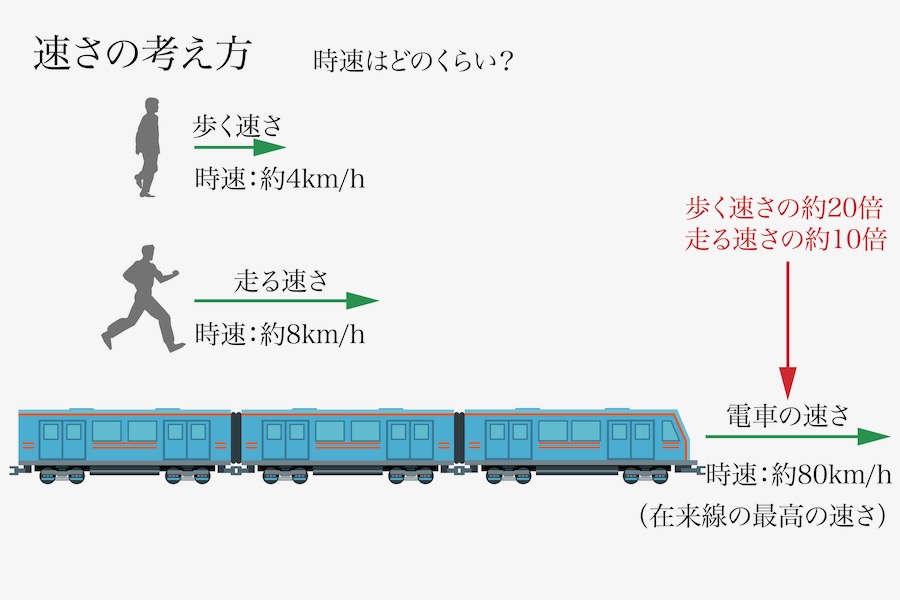
人の歩く・走る速さと電車の速さを比較して、具体的に「何倍違うのか」を考えました。

速さは、一般的に時速で表現されます。

「時速=1時間の間に、どのくらい移動する距離」です。

乗り物などの速さは「時速で考える」ことが前提となっており、

道路に大きく数字が描かれていますが、それは「最高時速」です。

このように、速さを考える際には「時速」が一般的ですが、今回は秒速を考えてみましょう。

「歩く速さ」「走る速さ」「電車の速さ」の秒速は、それぞれどのくらいになるでしょうか。

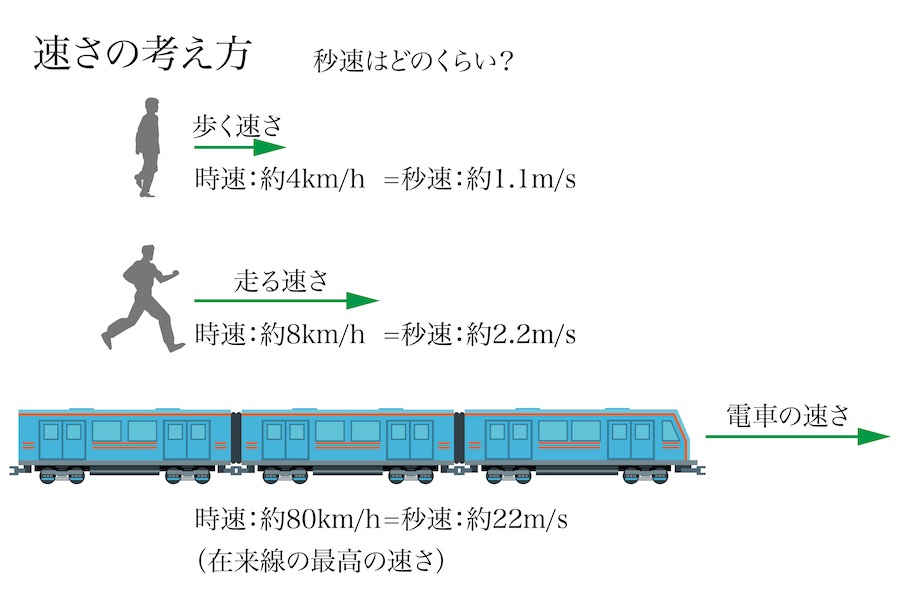
具体的に計算してみましょう。

上の単位「m/s」は「メートル・パー・セカンド」と呼びます。

英語で、1秒は”1 second”で、1メートルは”1 metre”なので、それぞれの頭文字が使われます。

日本語で書くと「m/秒」または「メートル/秒」となりますが、便利で世界共通なので”m/s”で表記します。

それぞれの秒速は、上の図のようになります。

歩く速さは「ちょうど秒速1m/s程度」で「1秒間に1m程度移動」となります。

それぞれ割り算しても良いですが、一番小さな「人の歩く速さ」を基準に考えも良いでしょう。

比較すると、素早く計算できます。

時速でも分かりやすいかもしれませんが、秒速にすると具体的なイメージが分かりやすくなります。

「たった1秒」の間で、電車は22m程も移動します。

つまり、電車が一番早い時は「1秒で校庭の25m走トラックを、ほぼ完走」します。

だいたいの計算の考え方「桁を合わせる・近づける」

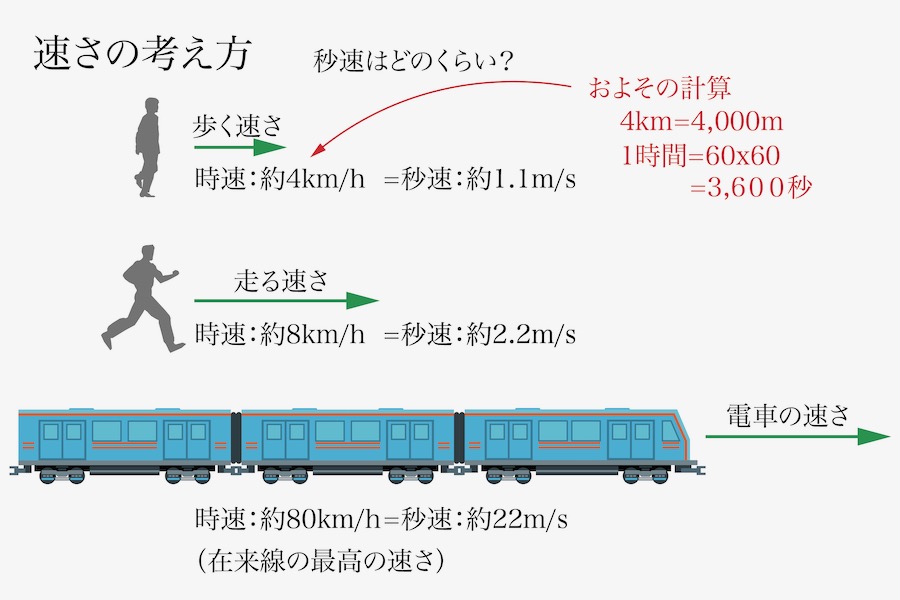
「時速から秒速に直す」計算の仕方を考えてみましょう。

しっかり割り算で計算しても良いですが、暗算で「およその計算」をしてみましょう。

まずは、「1時間=60分=60×60秒=3,600秒」です。

少し大きな掛け算を習うと当然のことですが、具体的に考えると「1時間は3,600秒もある」のです。

「およその計算」をする時には、「大体の桁が近くなるように」しましょう。

このような小さな桁の計算は、筆算で出来る小学生も多いかと思いますが、少し大変です。

そこで、先ほどの「だいたいの桁が近くなるように」しましょう。

「4km=4,000m」なので、これで「3,600秒と4,000で桁が近い（同じ）になる」のです。

割られる数（長さ）と割る数（時間）が、「同じ〜千」の単位になりました。

これで、考えやすくなりました。

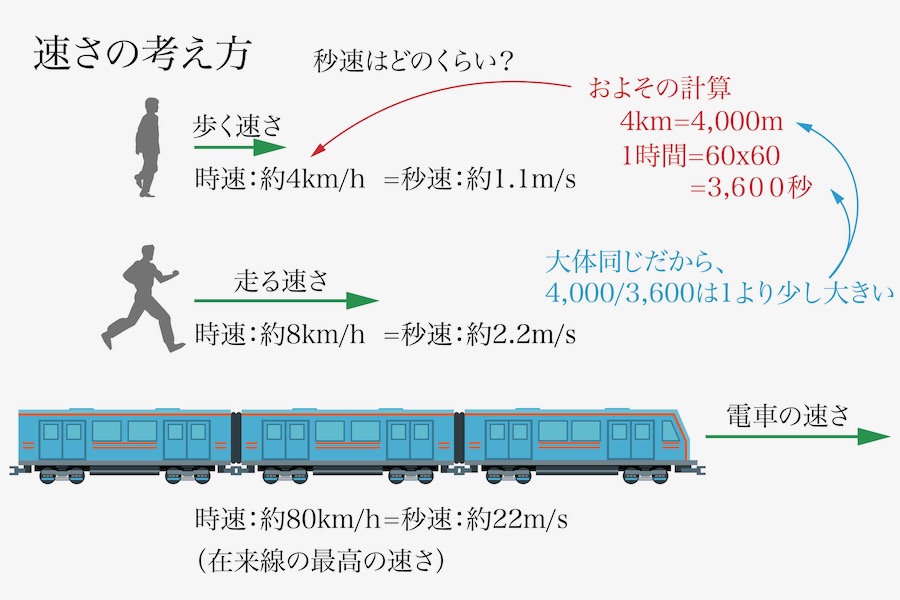
今回は「桁を近くする・合わせる」過程で、たまたま近い数になりました。

4,000と3,600は「だいたい同じ数」です。

ここで、

このように、「1より少し大きい」と考えましょう。

少し計算が早い方なら、

頭で計算して「4,000/3,600=1.111・・・」と計算するでしょう。

この時、このようにしっかり計算しても良いですが、

「だいたいの感覚」を考えるようにすると良いでしょう。

「だいたいで良い」と考えると、

「計算しないと分からない」ではなく、「だいたい分かれば良い」となります。

「だいたいの感覚」とテストの◯✖️：「考える自由」を持つ

この「桁を合わせる・近づける」計算の考え方は、様々な分野で有効です。

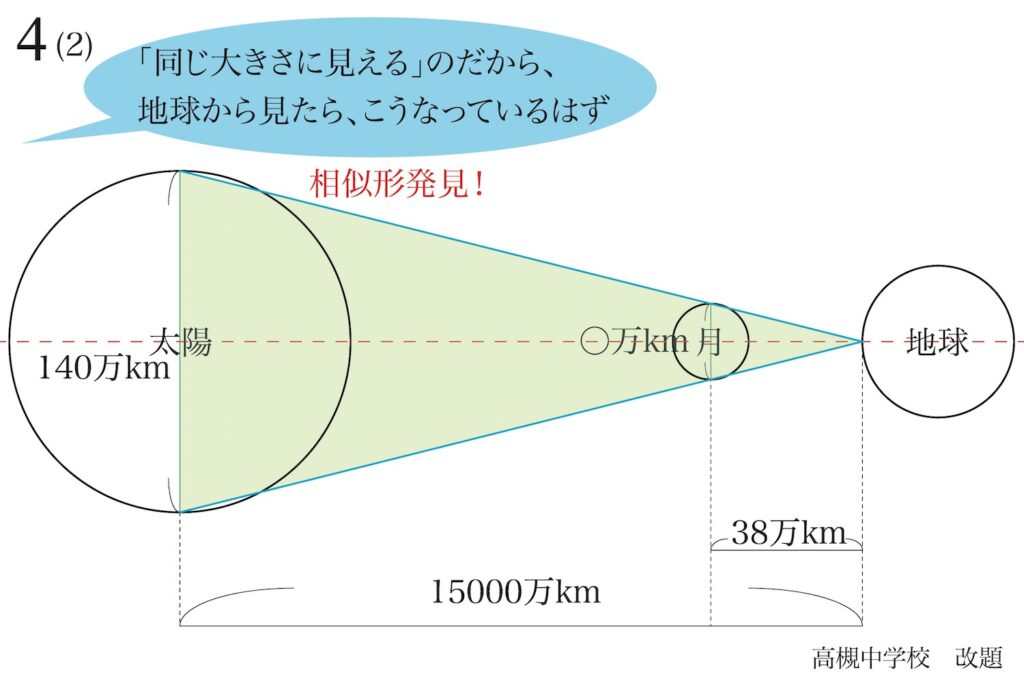
天体の問題を考えるときは、少し桁が大きく複雑な計算をすることが多いです。

天体の問題で「だいたい計算する」話を上記リンクでご紹介しています。

この時、「〜万km」という「想像できないほど大きなスケール」の距離が登場します。

「万」と言うのは「想像できそうで、想像しにくい」のが現実です。

世の中には「1万円札」があるので、「1円と1万円の違い」は想像できます。

一方で、「1kmと1万km」の違いは、「同じ1倍万の違い」なのにイメージしにくいです。

「算数・数学的に同じ」であっても、人間は「経験していないこと」はイメージしにくいのです。

そこで、こういう計算の際には、まずは「万=10,000」と直して約分するのが大事です。

今回考えた「歩く速さ」は「日常のスケール」で、天体は「非日常のスケール」です。

全然違いますが「だいたいの数字を暗算で考える」ことは、理科では大事な発想です。

「歩く速さ」は「約1.1m/s」ですが、「だいたい1m/s=1秒で1m」と考えましょう。

確かに「4,000/3,600は1.1くらい」と答えると、

場合によっては、算数（数学）のテストでは✖️になることがあるかもしれません。

「計算しなさい」という問題なら、「しっかり計算」しましょう。

一方で、いつも「試験（テスト）なら」を考えすぎない方が良いでしょう。

「だいたい」とか「どのくらい」と、日常の身の回りの理科や算数を考えてみるのも良いでしょう。

「テストで◯なのか✖️なのか」は、誰でも気になると思います。

それによって点数が変わり、場合によっては偏差値も変わる（下がる）ことがあります。

テストの点数は大いに気になりますが、

「テストではない時は、自由に考える姿勢」の方が良いと思います。

「◯なのか✖️なのか」は、算数（数学）や理科では比較的明確です。

算数（数学）の計算結果が、「時代によって変わる」ことはないでしょう。

一方で、理科や社会の考え方や「正しいこと」は「変わる可能性がある」のが現実です。

上のような、理科の天体に関する記述は「ある程度の決まった答え」があります。

一方で、「新たな発見」による「新たな学説」が登場する可能性もあります。

歴史も様々な研究者による学説があり、時代で解釈が変わることがあります。

有名な「本能寺の変」の「真の理由」に関しては、実に様々な学説があります。

2000年以降くらいから盛んになり、様々な歴史家などの方々が様々な説を展開しています。

小学校高学年のテスト・中学受験などで、「記述式」で答える試験があります。

「選択式」の問題と異なり、答えがたくさんある記述式問題。

意見を問う問題ならば、それぞれの人の考え方によって多様な答え方があります。

それこそが「多様性」であり、世界（欧米的感覚）では「多様性の実現」は重視・大事にされています。

「正しい答え」にこだわり過ぎると、記述問題ではつまづきやすい可能性があります。

「決まった答え」を答える問題を、解くことが多い中学受験生・高校受験生・大学受験生。

それでも、「考える自由」は自分なりに持つようにして、学びを進めと良いでしょう。

すると、勉強もはかどって学力も増強して、「志望校に合格する」可能性がアップするでしょう。

次回は下記リンクです。