前回は「かっ車の考え方・コツ・ポイント 3〜動かっ車の基本の理解・大事な「ひもの長さ」・動かっ車と定かっ車の複合問題・「基本を理解する」学びが近道・暗記と理解すること〜」の話でした。
動かっ車の移動距離を描く：どこかの点に注目
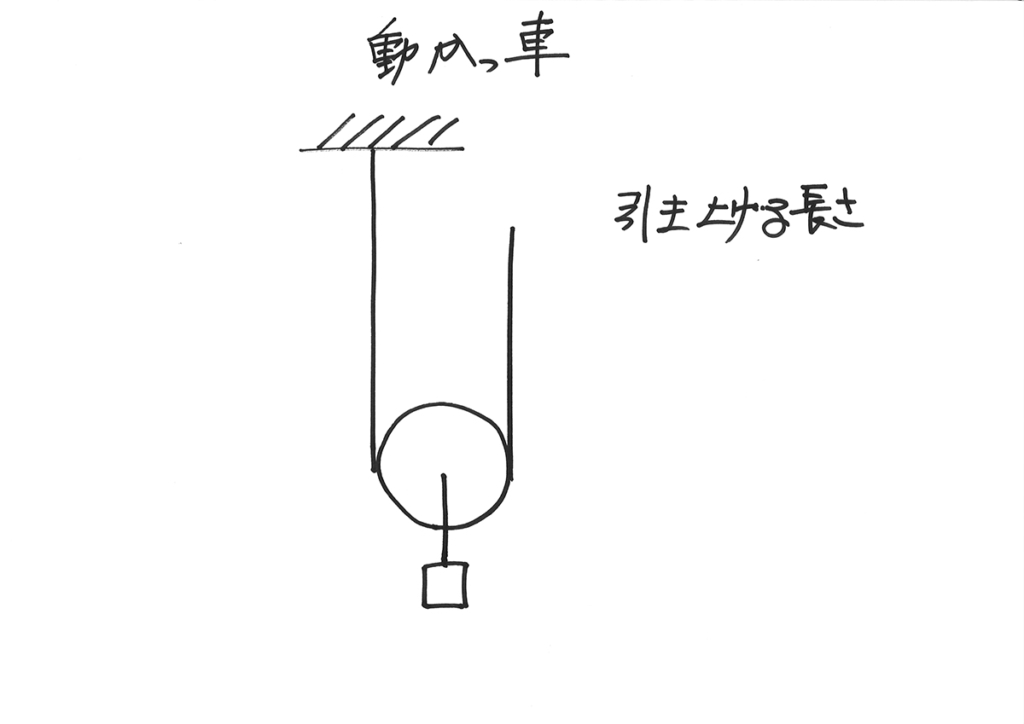
今回は、「動かっ車」の移動する距離を描いて考えてみましょう。
女子小学生これは知っているけど、
理由はよく分からない・・・
男子小学生おもりの移動する長さの
2倍、引き上げるんだよね。
動かっ車についたおもりを、引き上げる長さを具体的に考えてみます。
今回は重さは関係ないので、「重さの矢印」は描かないです。
図は出来るだけシンプルに、必要なことを描くことが大事です。
実際に、描いて考えてみましょう。
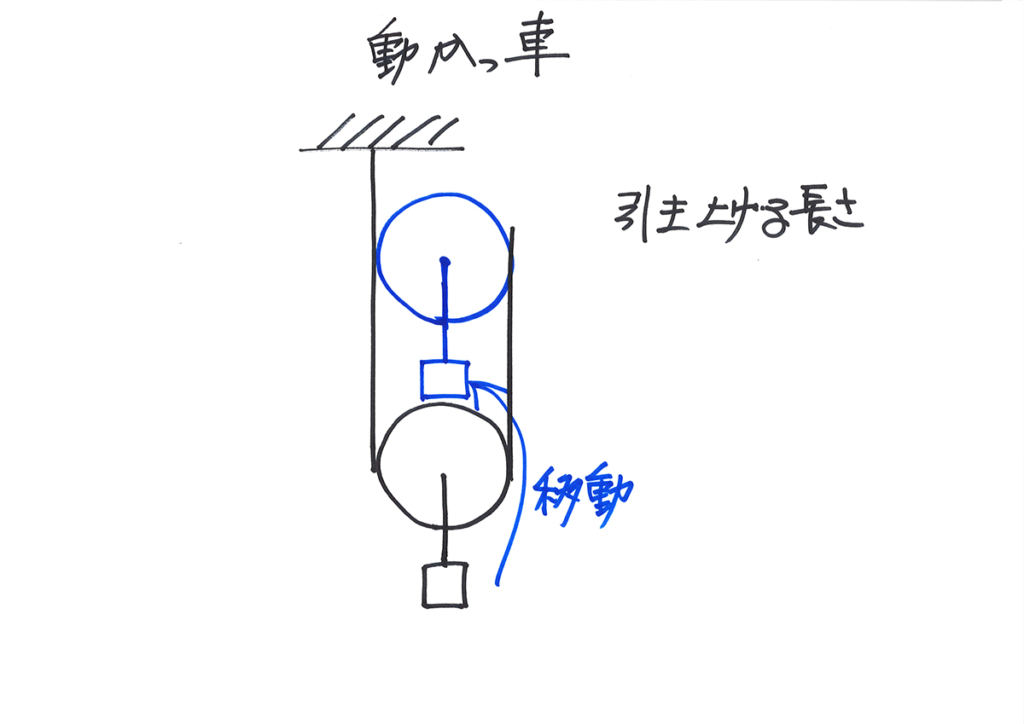
おもりを引き上げたら、おもりは上に移動します。
ここで「ひもをどのくらい引き上げるか」を、描きながら考えてみましょう。
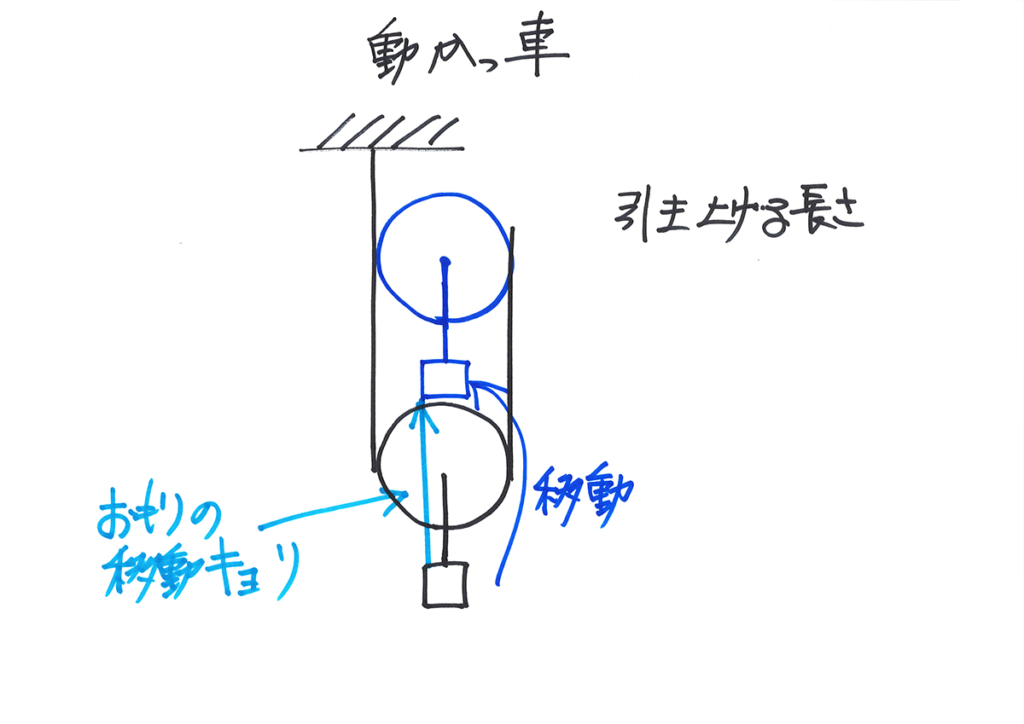
おもりの移動距離はわかりますが、「ひもとの関係」がなかなか分かりません。
男子小学生描いてみると、ゴチャゴチャして
よく分からなくなるけど・・・
ここで、「おもりの移動距離」は何か？を考えてみましょう。
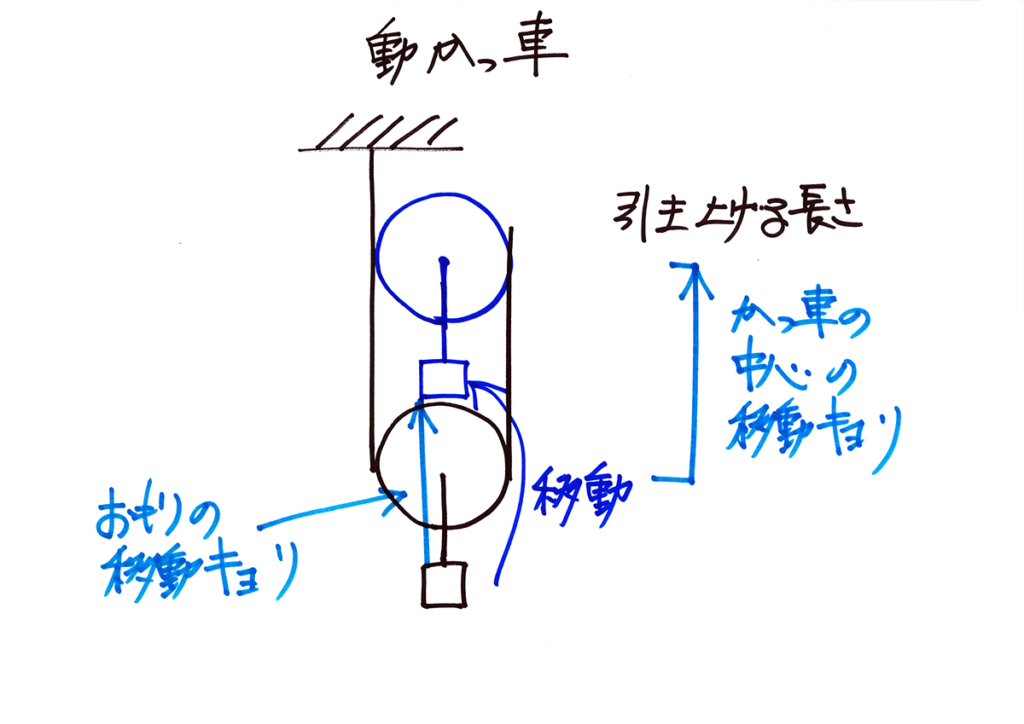
おもりと動かっ車は「つながっている」から、「おもりの移動距離=動かっ車の移動距離」です。
物や図形が移動する時は、どこかの点に注目するのが大事です。
今回は、動かっ車の中心に注目します。
すると、「おもりの移動距離=動かっ車の中心の移動距離」です。
女子小学生かっ車の中心の移動を考えると、
分かりやすいね！
これで、大分考えやすくなりました。
大事なポイントに注目
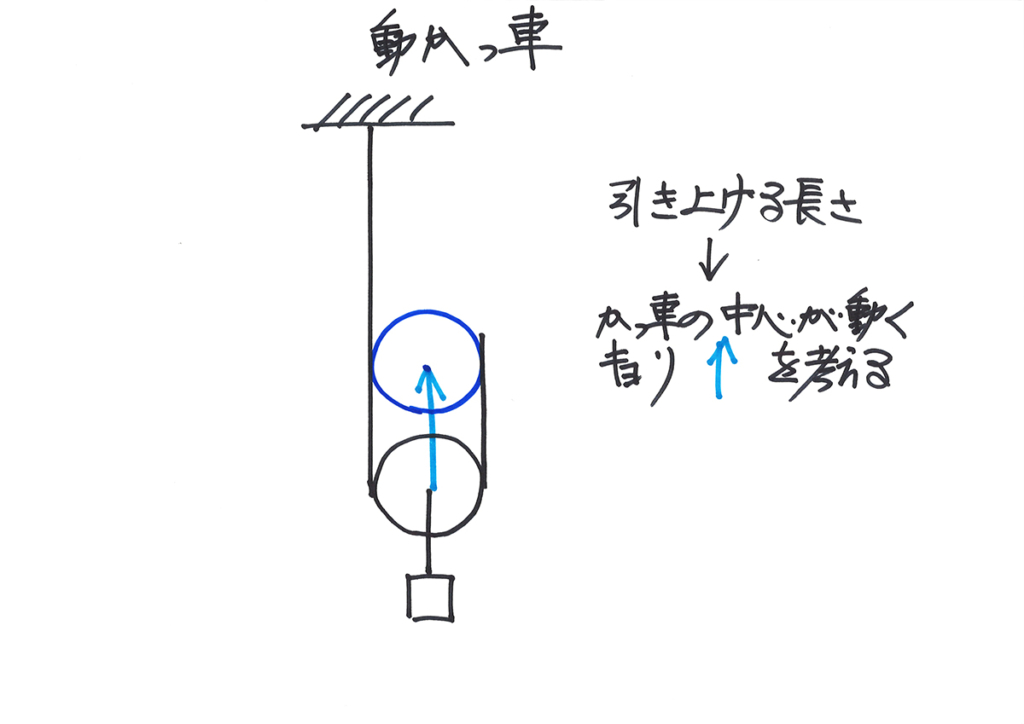
複雑で分かりにくい時は、「何が大事か」を考えましょう。
「かっ車の中心」ではなくて「かっ車の端」でも良いですが、中心の方が考えやすいです。
女子小学生おもりではなく、
「かっ車の中心」を考えるんだね。
女子小学生なんだか、
分かりやすくなった気がする。
そのちょっとした「わかりやすくなった気持ち」が大事です。
これで、だいぶ見通しが良くなりました。
「おもりの移動距離」と「引き上げる距離」を考えてみましょう。
黒鉛筆だと分かりにくいようでしたら、色鉛筆で描いてみましょう。
男子小学生色を変えて描くと、
分かりやすいね！
「おもりの移動距離=動かっ車の中心の移動距離」と考えました。
糸を引き上げることをイメージしながら、「動かっ車の中心の動き」を考えましょう。
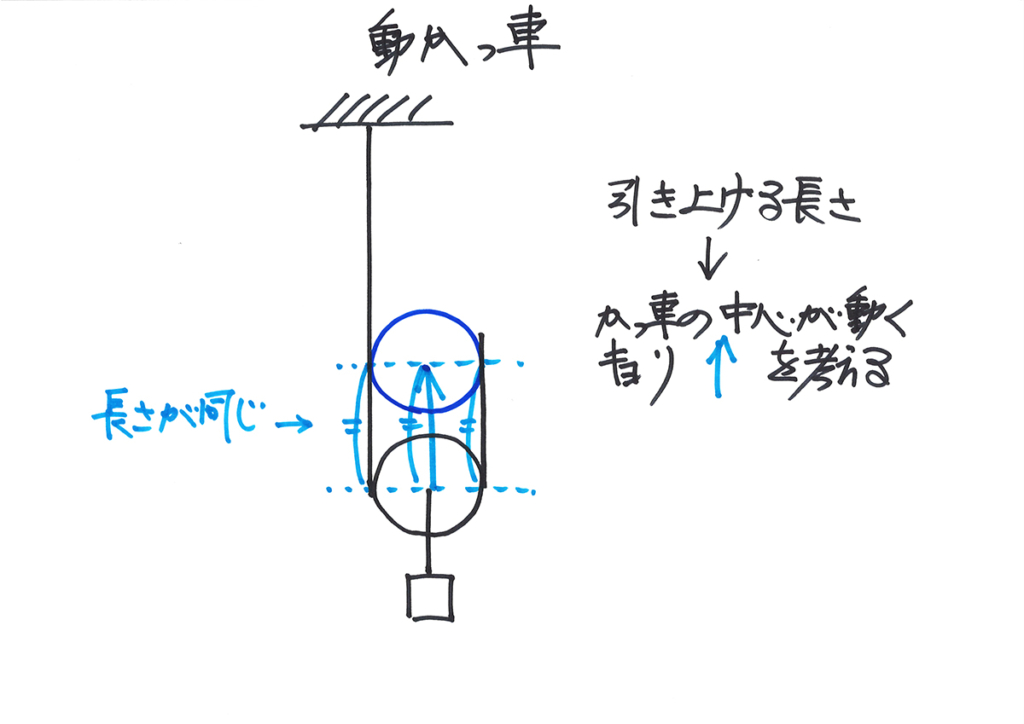
上図のように、「動かっ車の中心の動く距離=動かっ車の左右のひもの長さ」が図形的に分かります。
男子小学生この長さが同じなのは、
描くと分かるね！
このことを意識して、糸を引き上げてみましょう。
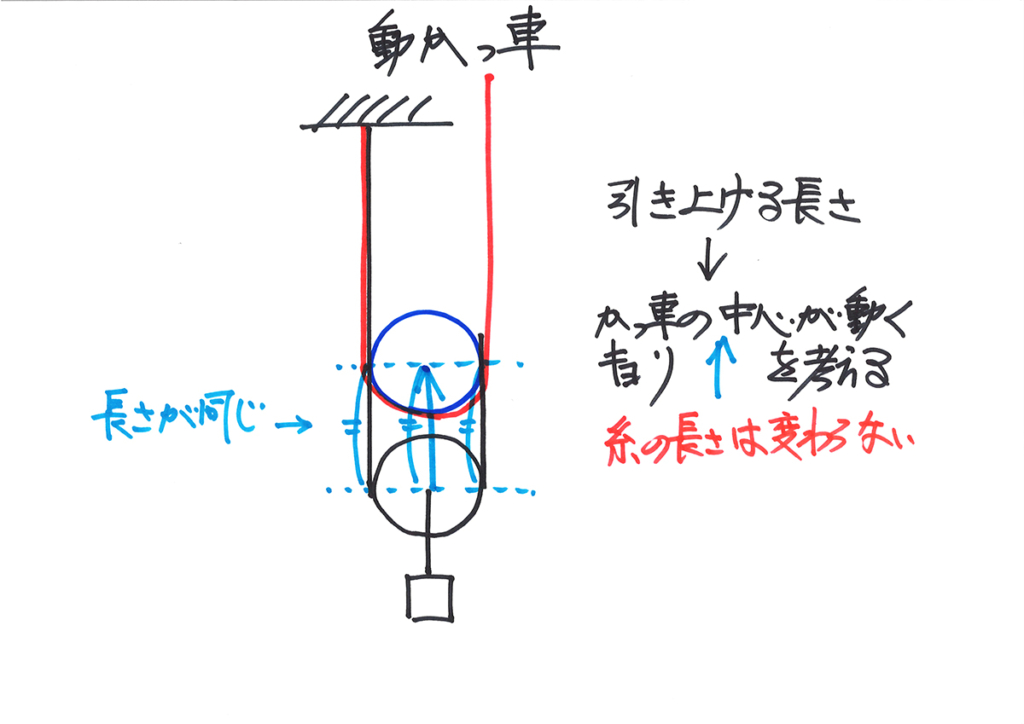
定かっ車の時と同様に、ひも・糸の長さは変わらないことに注目します。
女子小学生ここでも、
ひも・糸が大事なんだね。
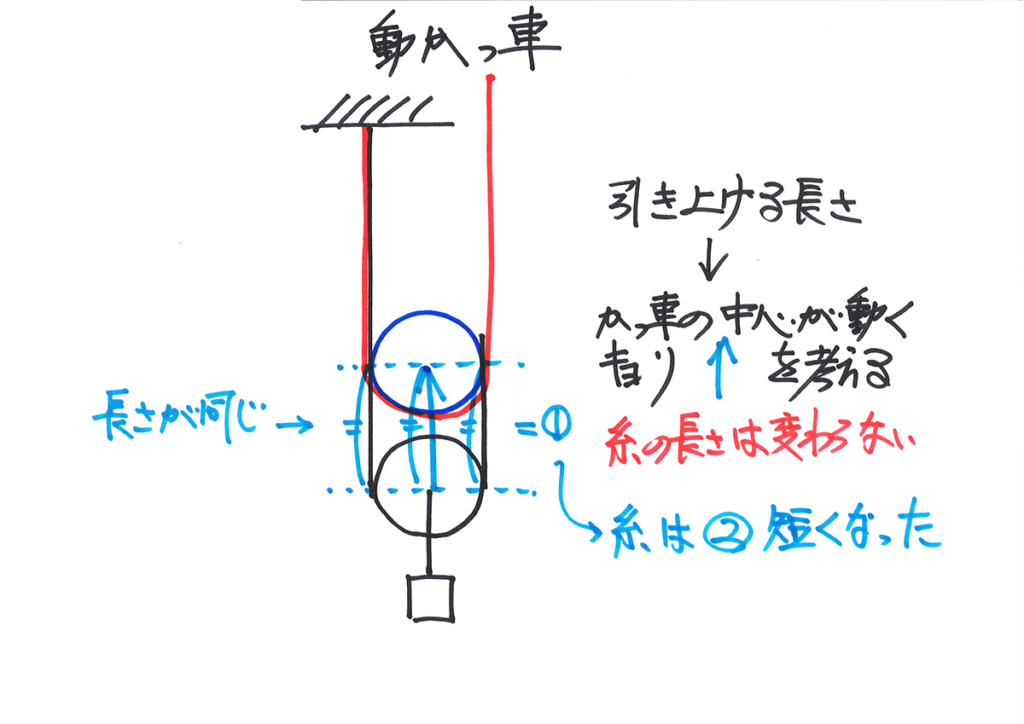
先ほどの「動かっ車の中心の移動する距離=①」とおくと、糸は②短くなります。
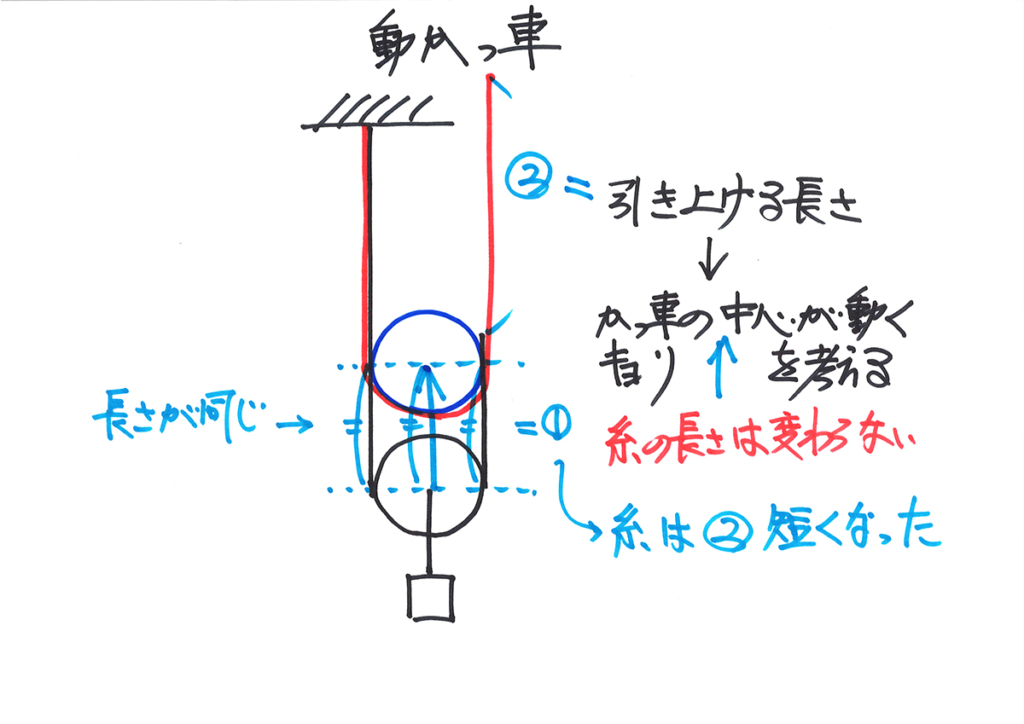
ここで、「糸の長さは変わらない」ことが大事です。
糸の右端は、②の長さ分、上に上がったことになります。
これで、「引き上げる長さ=おもりを引き上げる長さの2倍の距離」が分かりました。
男子小学生なるほど・・・
ちゃんと分かったよ。
女子小学生暗記していたけど、
こう考えると、よく分かった！
理解して楽しく成績アップ
「動かっ車が〜個あると、引き上げる長さが〜倍」などを暗記しても良いです。
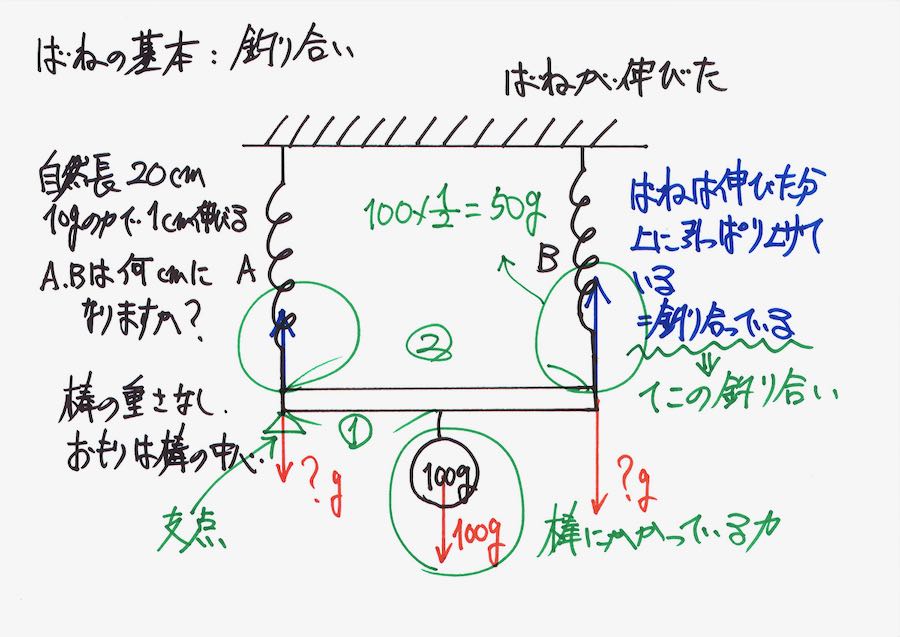
てこの問題では、「長さがおもりの逆比」という事実を「暗記する」と早く解けます。
これらの「力が〜倍」「長さが〜倍」「長さが重さの逆比」などを理解することが大事です。
力・ものの動き・ばねなど（力学）や電気は、このようにしっかり理解する方が楽しいです。
理由をしっかり理解しながら、学ぶ楽しさを感じて欲しいです。
男子小学生ただ暗記するよりも
楽しい気がする！
女子小学生自分が「かっ車」を目の前で、
動かしている気持ちになる！
「実際にかっ車を動かしているイメージ・気持ち」を持つと良いでしょう。
楽しくなると、無理に暗記するよりも主体的に学ぶので、学力が上がります。
きちんと理解することが、力・ものの動きなどの問題に対する応用力が、大きく上がります。
定かっ車・動かっ車の基本をよく理解したら、これらが複数ある場合を考えてみましょう。
「パターン化して覚える」ではなく、かっ車の動き・引き上げるイメージを考えると良いでしょう。
「ひも・糸の本数が〜本の場合は〜」が「暗記」ではなく「感覚的に分かる」ようになるでしょう。
次回は下記リンクです。
