「分からない」が「分かる」になる小学校6年生の勉強法〜異なる補助線から学ぶ図形の本質・補助線を比較・辺の比・平行な直線の意味と相似形を発見・面積比・同じ辺を共有する図形〜｜中学受験・算数

前回は「算数の成績アップの学び〜「大事な一冊」と他の問題集と参考書・少し早めに受験生向けの月刊誌に触れる・来年をイメージ〜」の話でした。

異なる補助線から学ぶ図形の本質：補助線を比較

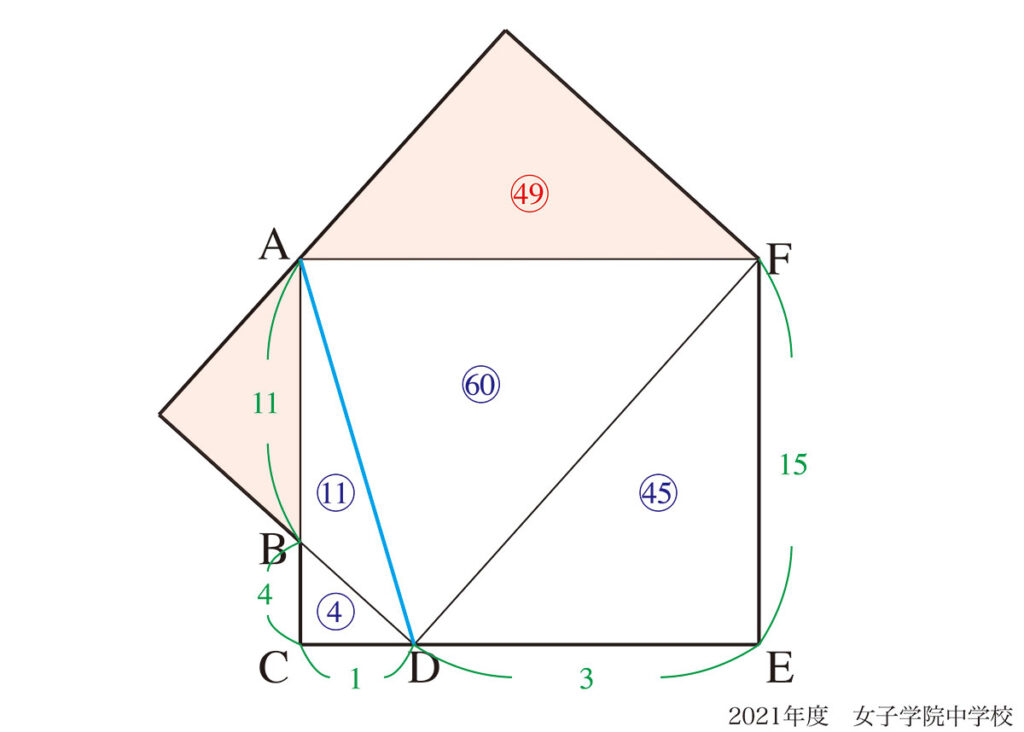
算数実践の問題1では、最も本質的で良い補助線は上の解法Aの青色の補助線です。

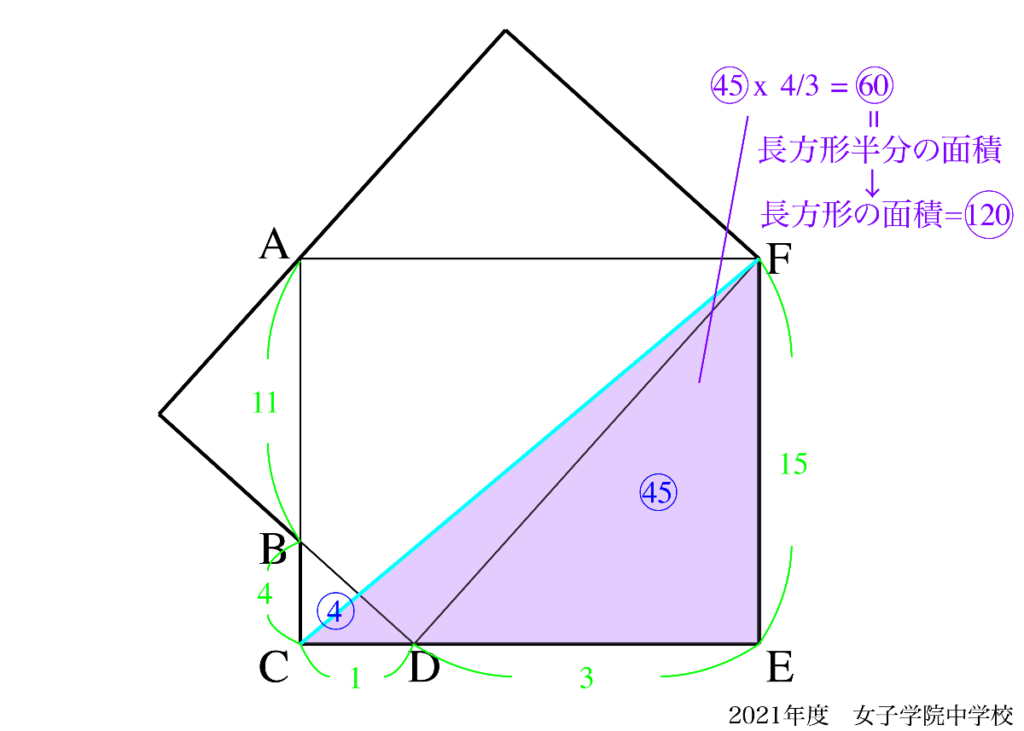
少し遠回りになりますが、この問題は上の解法Bの補助線でも解くことが可能です。

二つの解法は上記リンクでご紹介しています。

ここでは、「最も良い補助線」と「最善ではないが解ける補助線」によって考えています。

自分で手を動かして色々と考えると、とても良い勉強になります。

これらの補助線を、「自分なりに比較してみる」と良いでしょう。

解法Aの補助線は、なぜ良いのでしょうか。

解法Aの補助線が解法Bの補助線より良いのは、いくつか考えられます。

上のa,bの視点は非常に大事なポイントです。

他にもポイントがあるかもしれませんが、これらを意識すると良いでしょう。

辺の比：平行な直線の意味と相似形を発見

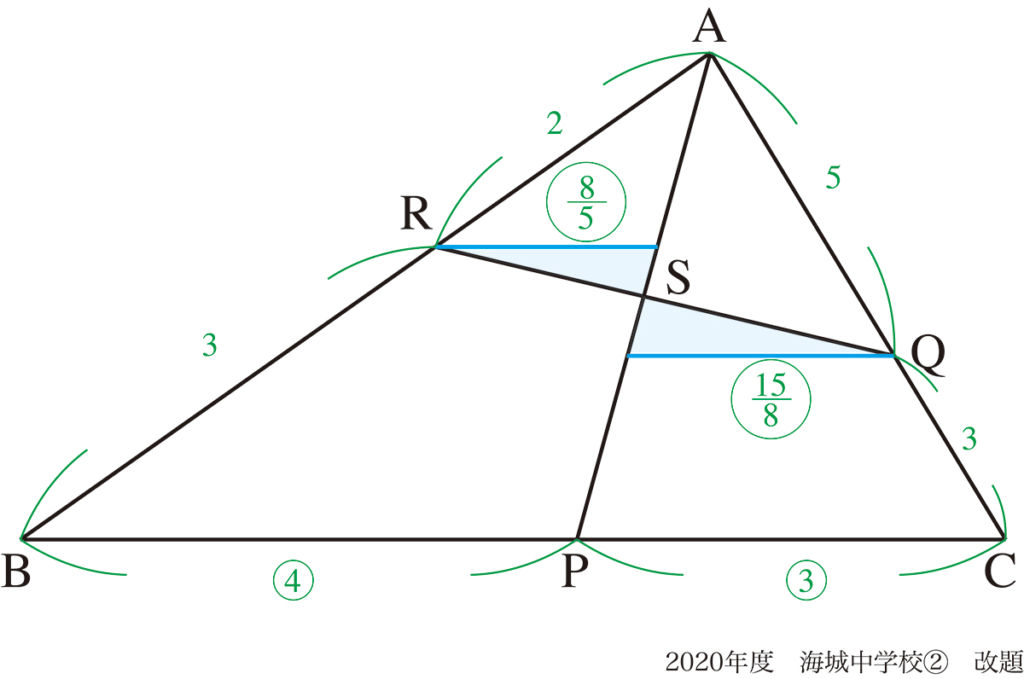
三角形に様々な線が引かれて、辺の比を求める算数実践の問題2も良い問題です。

典型的でシンプルな図形問題ですが、辺の比、面積比を考えた解法を紹介しています。（上記リンク）

どちらかというと「辺の比」を考える方が素直ですが、ぜひ両方ともしっかりと理解して下さい。

ここで二つの考え方の「考え方の方向性」をしっかり理解しましょう。

「平行な直線を補助線にする」考え方は最も大事なので、平行の意味を復習します。

「全く同じ向き」を向いているのが「平行」です。

平行な直線があると「錯覚と対頂角が同じ」で相似形が沢山見えてきます。

「なぜ、平行な直線がポイント・鍵になるのか」をもう一度考えてみると、

このように、色々考えると図形を解く力が上がるでしょう。

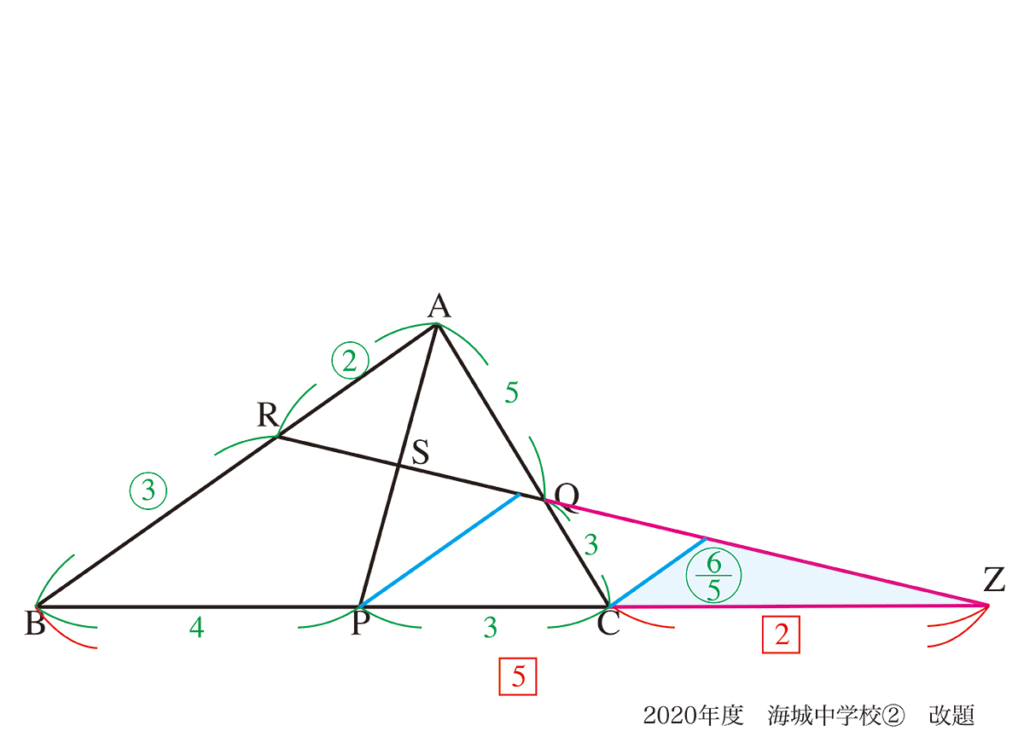
「図形のある辺に平行な直線」を引くとき、図形の外側に出てゆく場合があります。

この「図形の世界を広げる」考え方はしっかり出来るようになりましょう。

少し遠回りに感じる方もいるかもしれませんが、「平行な直線を引く」と解ける可能性が高いです。

慣れれば、図形の内側でも外側でもスイスイ比を考えられるようになるでしょう。（上記リンク）

これは「何か鉄則を学ぶ」よりも、「平行な線を自分で引いて考える」と良いでしょう。

面積比：同じ辺を共有する図形

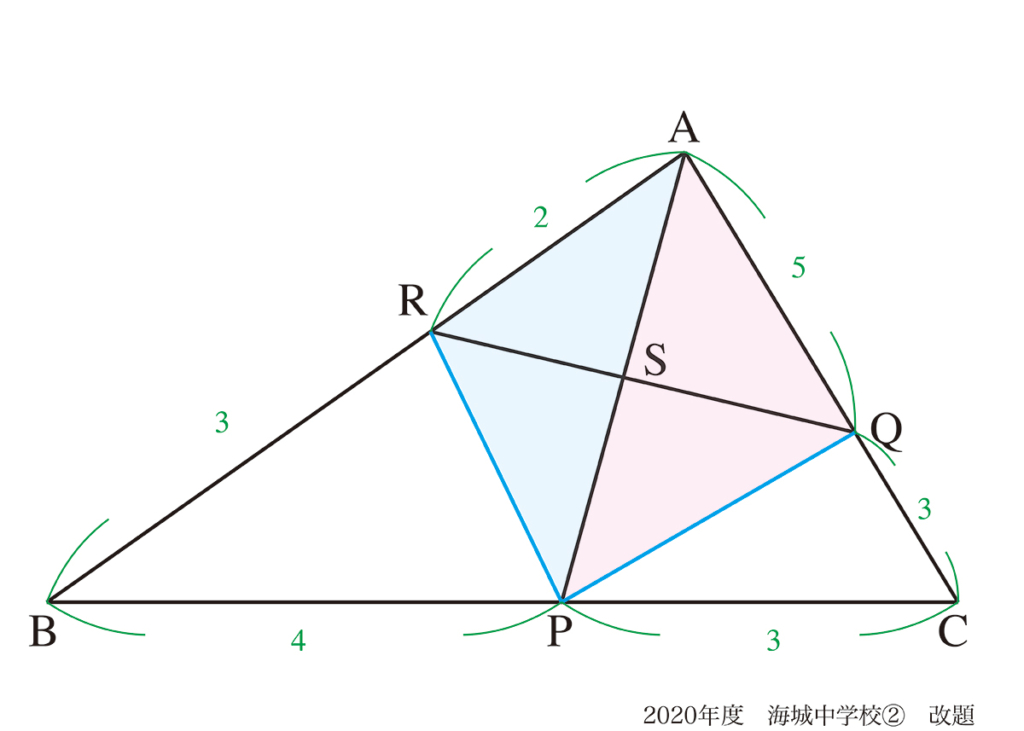
この問題は面積比に注目すると、比較的素直に解けます。

すっきりと図形を分割している点がポイントです。

問題1の解法Aの補助線にも共通しますが、「図形をきれいに分割」している点がポイントです。

ここで、「図形がきれいに分割できない=新たな交点が出来る、余る図形がある」線は、

あまり上手くないことが多いです。

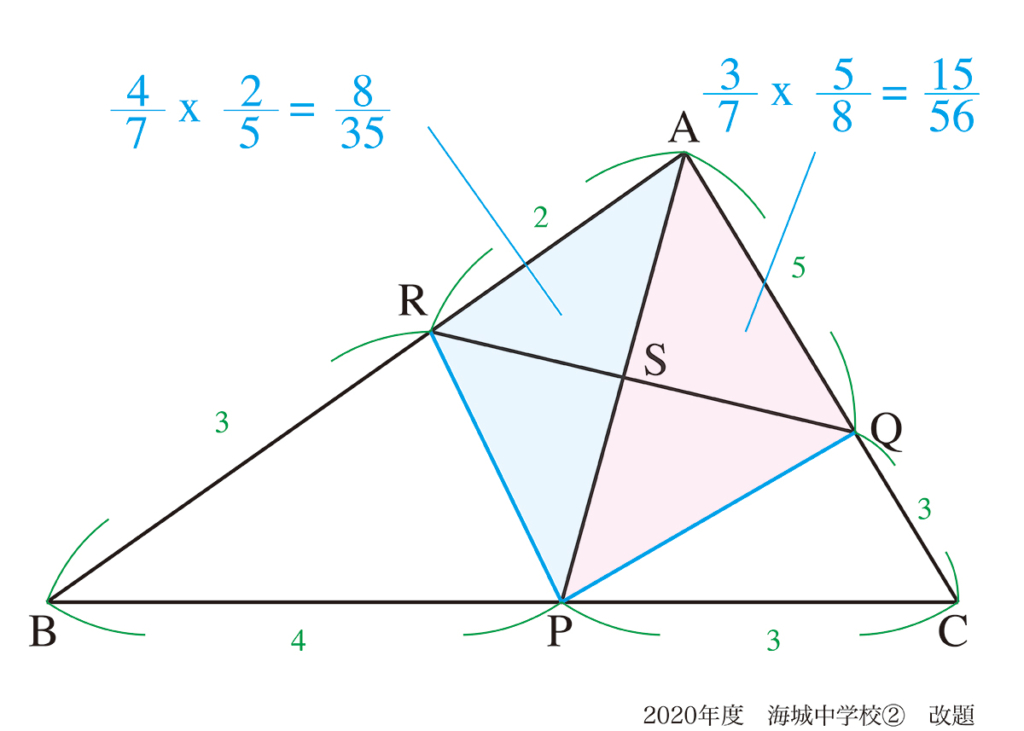
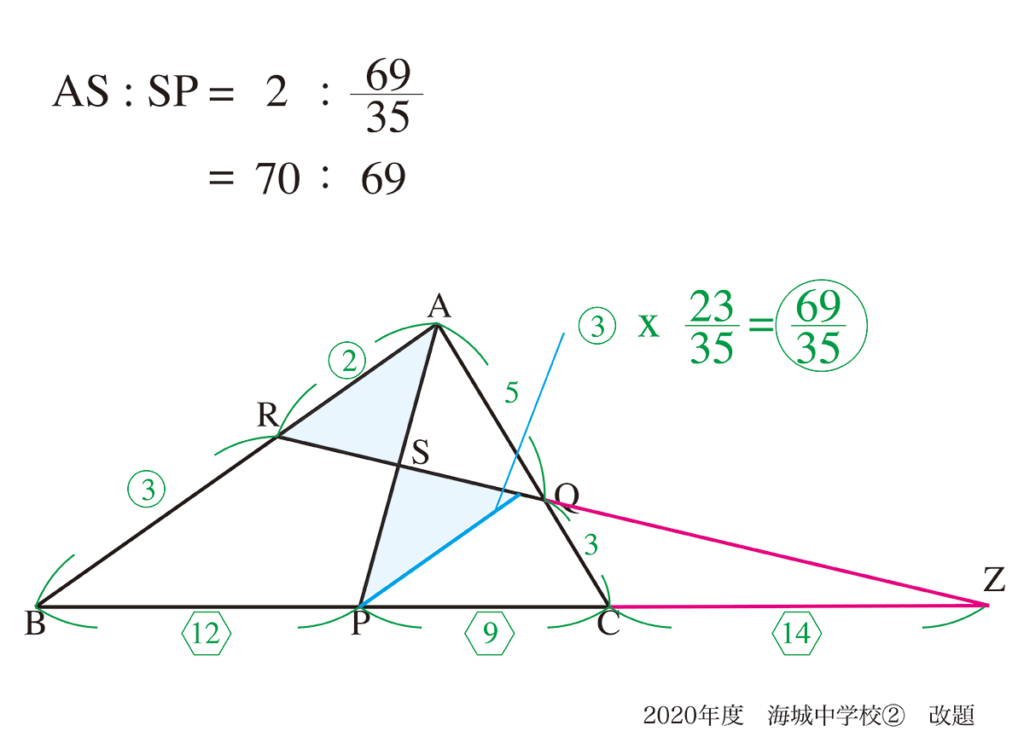
この問題では、図形をきれいに分割して、解く対象の辺と面積比が連動しやすいのがポイントです。

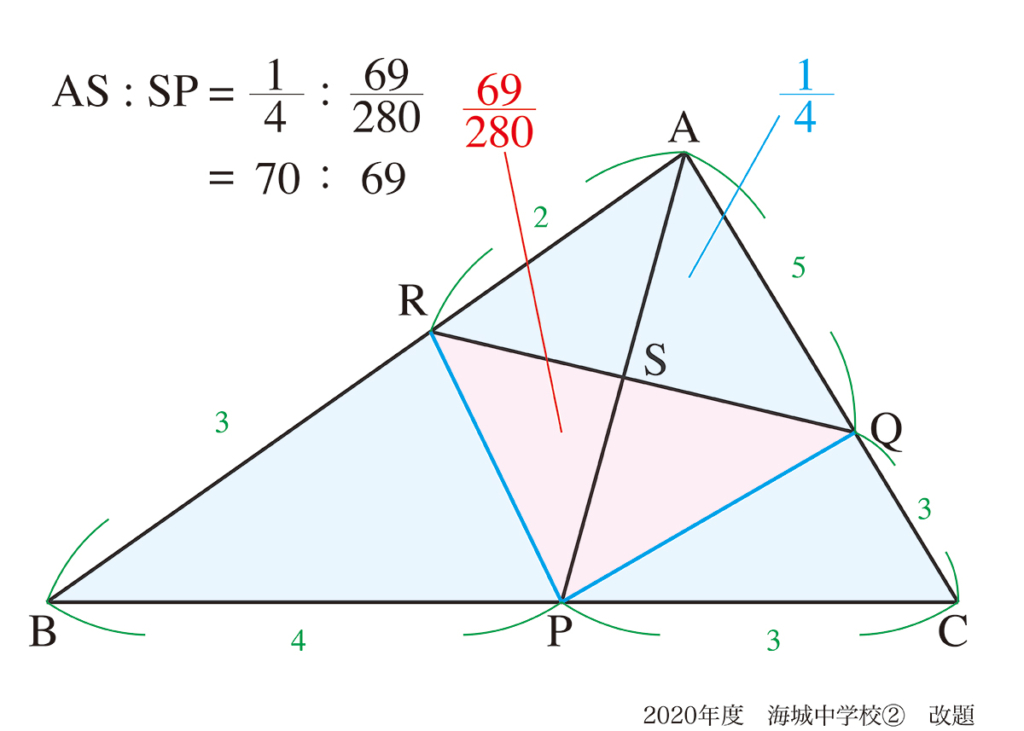
特に(2)の解法では、計算が少し大変ですが、図形がきれいに分割できているので考えやすいでしょう。

これは、どちらでも良いですが、両方できるようにしましょう。

そして、描いて考えていると「辺の比と面積比のどちらが良いか」が初期段階でわかるようになります。

応用問題・難問に取り組む方は、「ただ解く」ではなく「何が良いのか」を考えましょう。

そのように「深く考える姿勢」によって、「1題解くことが数題分に匹敵」するでしょう。

解いたことがある良い問題を、もう一度じっくり深く考えてみましょう。

「良い問題をじっくり深く10題考える」は「良い問題をサッと100題考える」以上の効果があるでしょう。

深く考えると「思考の軸」が生まれて、応用問題・難問を解く力が大きく上がります。

小学校6年生の受験期後半以降は、一題をしっかり習得しましょう。

特に第一志望校の過去10年分の問題は、

このくらい深く学びましょう。

これは「暗記する」ではなく、「深く考えたら、覚えてしまった」状態です。

このような状態を目指して学ぶと良いでしょう。

次回は下記リンクです。