前回は「「自分の好きな科目」が自然と見つかる学び〜得意科目の発見と学びの進化と深化・英語の入学式と卒業式・OrientationとCommencement=始まり〜」の話でした。
中学3年から高校1年での学問の大きな変化
中学受験の際の成績と、中学1〜2年生頃の成績は「大体似ている」傾向があります。
中学生になると「算数」が「数学」に変わり、場合によっては「代数」や「幾何」が始まります。
「数学の基礎」とも言える算数ですが、やはり算数と数学では大きく異なります。
数学と「学問の学」の字がついている通り、数学は学問的傾向が強くなります。
それでも、中学1~2年生の数学は概ね「算数の延長線上」にある傾向があります。
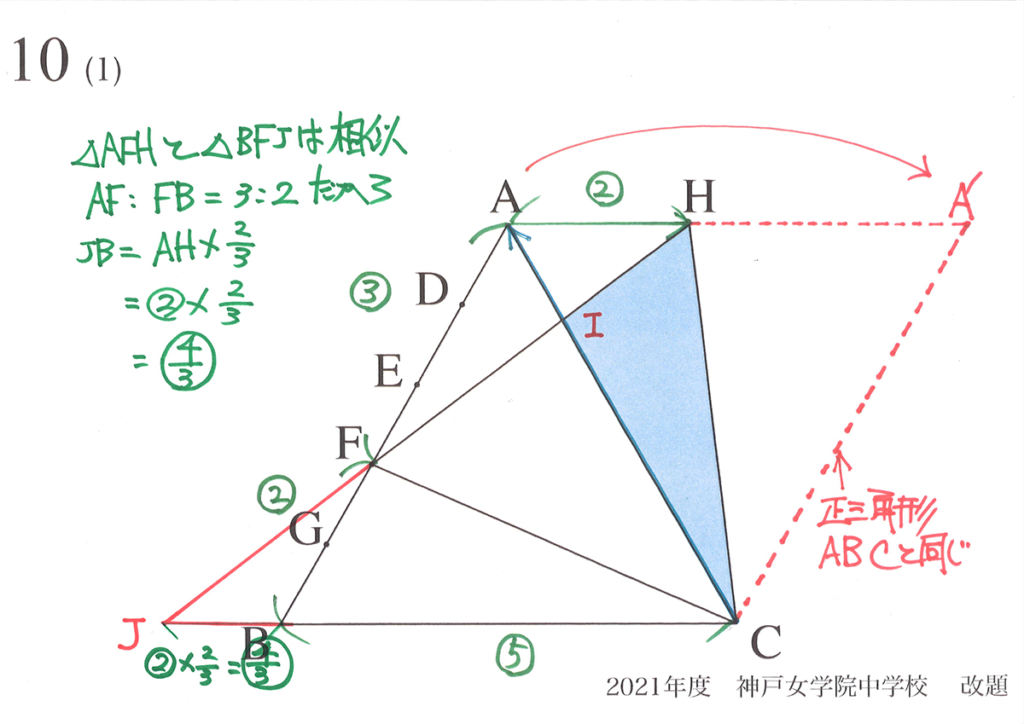
大きく異なるのは幾何学で、小学校の「算数の図形」とは全然異なります。
「算数の図形問題」の難問は多数ありますが、基本的法則・原理は非常に少ないです。
それに対して、幾何学は円に関する様々な性質や定理などが登場し、一気に複雑化します。
数学科教師A円に接線を引いて、
この様に円周角を取ります・・・
数学科教師Aすると、この角度と
この角度が必ず等しくなります・・・
数学科教師Aこれは「接弦定理」と言って、
とても大事です！
「小学校の算数の図形」が一気に複雑化する幾何学以外は、
男子中学生代数は、中学受験の
算数と似ているところがある・・・
中学2年くらいまで「算数の延長」となります。
これが一気に、大きく変化するのは、中学3年〜高校1年です。
学校のカリキュラムにもよりますが、この中学3年〜高校1年の頃に様々な変化があります。
代数は代数学に一気に近くなり、数学らしさが急速に高まってゆきます。
女子中学生なんだか、最近
たくさんの定理が登場してきた・・・
「理科の延長」だった「なんとなく物理」が、一気に「本格的物理の基礎」と変化するのです。
運動方程式・エネルギー保存則などを学ぶようになり、「物理学の非常に大事な基本」を学びます。
男子中学生エネルギー保存則、
ってなんだろう・・・
イメージすることを楽しむ物理・化学実験
これらの物理法則などを暗記するのは簡単ですが、暗記しただけでは、ほとんど意味がありません。
法則は「公式」として習うことが多いのが現実です。
公式をきちんと理解して、自分で立式してゆく必要があります。
この「立式する」ことは、物理学の非常に根幹的な部分です。
基本的な問題から学んで、徐々に様々な状況を描いて、働く力などをイメージして、描きこみます。
それらの力をもとに立式して、問題を解いてゆきます。
この時、「イメージする力」は非常に重要です。
状況がよく分からないのでは、立式しようがないからです。
「イメージすること」の話を、上記リンクでご紹介しています。
小学生の頃から「イメージすること」を楽しんでやってきた子は、こういうことは得意だと思います。
あまりそういう経験がない中学〜高校生の方は、今からでも遅くないです。
物理・化学などの実験は、積極的に楽しみながら取り組んでみましょう。
中学3年くらいになると、大体自分の方向性が出てきて、
男子中学生僕は、数学や物理が好きだから、
理科系だな！
女子中学生私も数学結構好きだから、
理系に行きたい！
男子高校生僕は数学は性に合わないし、
英語とかの方が好きだから、文系かな！
大きく理系・文系に分かれてきます。
大学の「理系・文系」の分類に関しては、「意味がない」と言う意見もあります。
ところが、現実的に中高生の学びにおいては、「文系と理系の違い」は大きいのが現実です。
両方出来る子もいますが、多くは、
男子中学生数学得意だけど、
古文はちょっと・・・
女子中学生英語が好き！
授業が英語ばっかりだと良いのに・・・
自分の指向性に応じて、得意・不得意や「楽しい・楽しくない」科目が出てくるでしょう。
その自分の気持ちを大事に、「やりたい科目」は、どんどんやりましょう。
失敗を楽しんで考える姿勢：失敗が大発見につながること
物理が、どんどん「本格物理」になってきて、実験が増えてくる学校が多いと思います。
実験は結構大変で、うまくゆかないこともあります。
男子小学生物理楽しいけど、
実験が予想と違ったよ。
男子小学生僕、物理は好きだけど、
あまり向いてないのかな・・・
実験は「うまくゆかない」ことも楽しんでみると良いでしょう。
うまくゆかないことから、何か発見があることがあります。
ノーベル賞受賞者のの中には、
サイエンティストTあれ？
なんかいつもと違うぞ・・・
「予想しなかった状況・事態」を「ただの失敗」と思えないで、考えた方も大勢います。
サイエンティストTなぜ、
こんなおかしなことになるんだろう・・・
そして、研究した結果、
サイエンティストTあっ！
こんな大発見があったぞ！
「新発見」となることもあるのです。
男子中学生えっ？
失敗しても、新発見になるの？
「失敗→新発見」ではありませんが、そのような可能性もあります。
そこで、「失敗もまた良し」と思いましょう。
うまく行かなかったら、がっかりせずに
男子中学生先生・・・
この辺が上手くいかなかったんですが・・・
「上手く行かなかった実験結果」を物理の先生に話してみましょう。
物理の先生Oなになに、
どんなところが上手くいかなかったのかな？
先生も楽しんでくれるでしょう。
そういう姿勢が将来的に非常に大事で、「失敗を考えてみる」と学力も上がるでしょう。
次回は下記リンクです。
