前回は「難しい記述問題の考え方・書き方・書けるようになる勉強法〜グラフに線を引いて理解・傾向を浮かび上がらせる線・直線を引く考え方・一本の線が大きな効果を生む・グラフをじっくり読んで「面白い」と思う気持ち・思考を深化〜」の話でした。
一本の線を入れて分かること：武蔵らしい図表とグラフがある記述問題
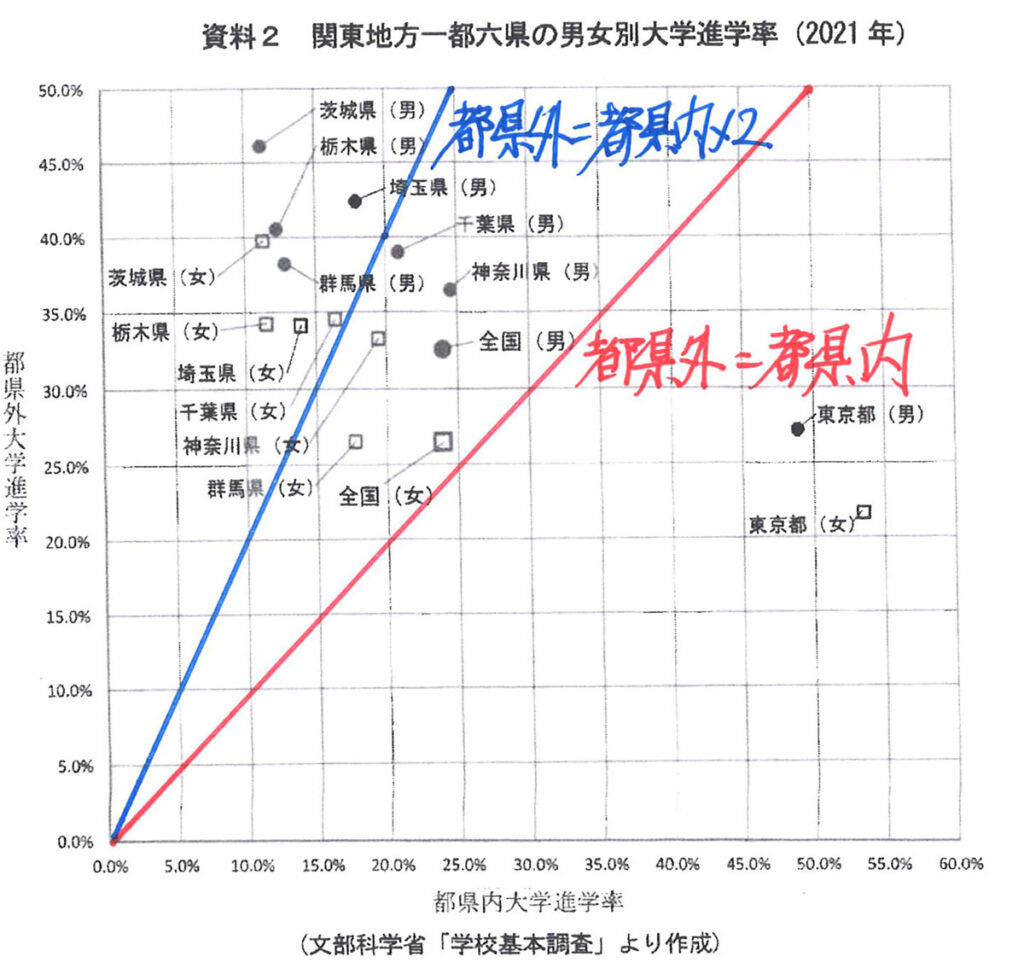
この武蔵中の問題は「学校制度」という切り口で、各国との比較、歴史、社会に関して論じています。
そして、図表とグラフが一緒に提示されており、非常に武蔵らしい問題です。
問題とは関係ありませんが、上記のような青色の直線を引いてみました。
これで、様々な特徴がグラフから見えてきました。
問題にある、座標（縦軸と横軸の数字）だけでも、大きな傾向は、ざっと分かります。
そこに、「一本の線を入れることで、非常に明瞭にわかる」ことが実感できたと思います。
うん。
点だけの時と、全然違うよ。
たった一本直線を入れるだけで、
こんなに見え方が違うのね。
一本（赤色）入れて、そしてもう一本（青色）を追加してみました。
もう一本、簡単な直線を入れてみましょう。
もう一本？
どうしたらいいの？
こういう「何かをしてみる」時は、「どうしたら良いか」を考えすぎずに「やってみる」のが良いです。
もう一本の線から分かること：様々な特徴を理解する姿勢
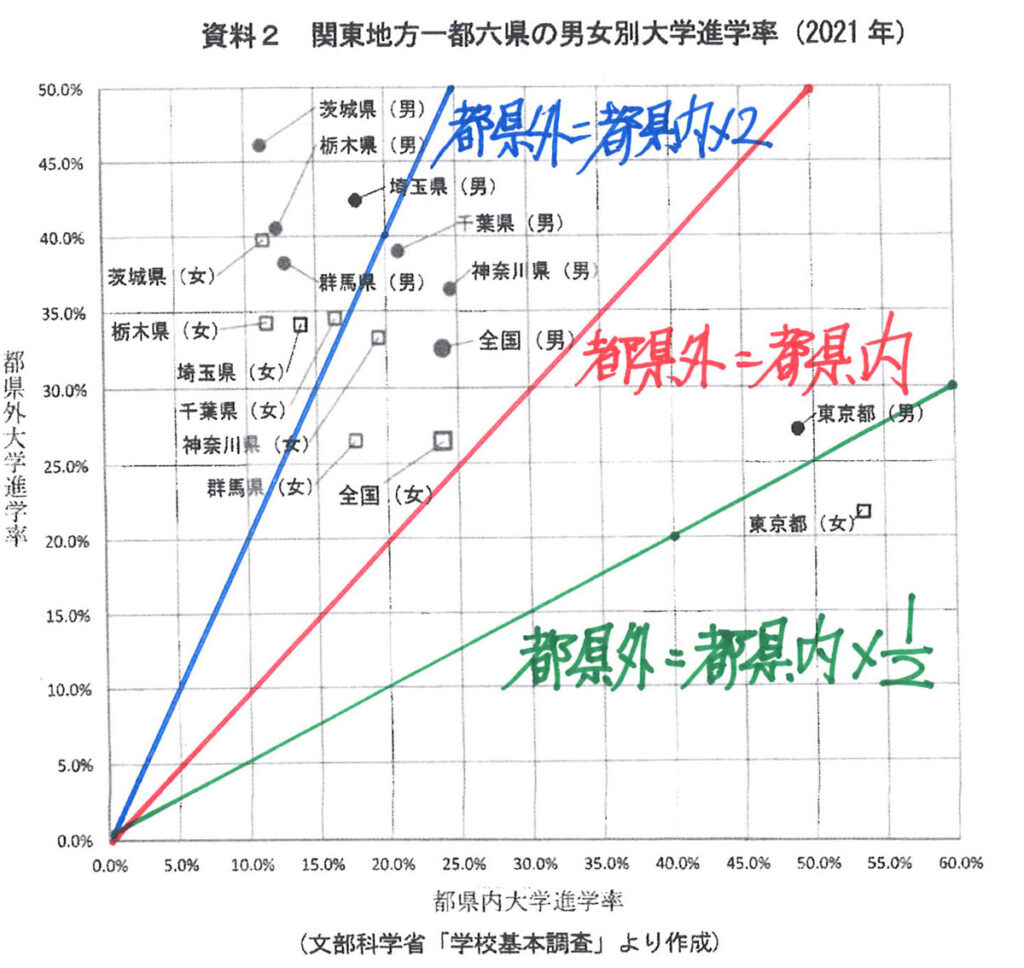
一例として、上のような直線が考えられます。
「都・県外の進学率=都・県内の進学率x1/2」の直線（緑色）です。
前回の「青色の直線の傾向」の逆となります。
今度は、都・県外に進学する人が
非常に少ない傾向の線だね！
さっきの青線は、
都・県外の進学率が都・県内の進学率の2倍で・・・
今回の緑線は、
都・県外の進学率が都・県内の進学率の半分ね！
この直線より下は、「都・県外の進学率=都・県内の進学率の半分以下」となります。
つまり「同じ学年の1/3以下が、都・県外の進学」となります。
あれ？
なんで「1/3以下」って分かるの？
分かりにくい時は、比を数字に置き換えてみましょう。
この緑線のラインは、
都・県内の進学率 = ②
と置くと、
都・県外の進学率 = ① = ② x 1/2
となります。
あっ！
分かった！
全体が③になるから、
都・県外の進学率①=全体の1/3ね！
だから、緑線の下は、
「都・県外の進学率は全体の1/3より少ない」だね。
これも
面白いね。
東京の女子だけが、
緑色の線の下だね！
東京の男子だけが、赤と緑色の
間にある。
大きな傾向が出てきました。
東京都の女子が「都外に進学するのは、大学進学者の1/3（33%）以下」です。
グラフを読む：具体的傾向と数値を読んで理解を深める
問題にはありませんが、実際に数値を読んでみましょう。
「東京の女子の都外の進学率」は、どのくらいでしょうか。
21%と22%の
間かな・・・
21.5%くらい
かな・・・
「グラフから読み取る数値」は大体で良いので、21、21.5、22%のどれでも良いでしょう。
・あまり厳密に考えすぎないで、小数点以下は四捨五入・切り上げ等でもOK
・理科の実験などは、誤差が必ずあるので、だいたいの傾向が大事
グラフを作る問題は、
あまりやったことないけど・・
なんか
難しそう。
「グラフを読む」のと「グラフを作る」ことの大きな違いが分かったと思います。
「大きく違う」のですが、難しく考えすぎないで「どういう傾向が分かるか」と考えましょう。
「グラフを描く」問題は少ないですが、いくつかの学校で出題が見られます。
曲線の時、
描くのが難しい・・・
直線は
いいけど・・・
曲線の時は、
どういうふうに曲げれば良いのかな・・・
「曲線を描く」時も、あまり難しく考えないようにしましょう。
曲線は「色々な形」がありますが、中学入試では「大体の曲線」が描けていれば○です。
少し寄り道しましたが、記述式はこのように
他に
何か考えられないかな・・・
と考えてみましょう。
こう考えたら、
どうだろう・・・
も良いでしょう。
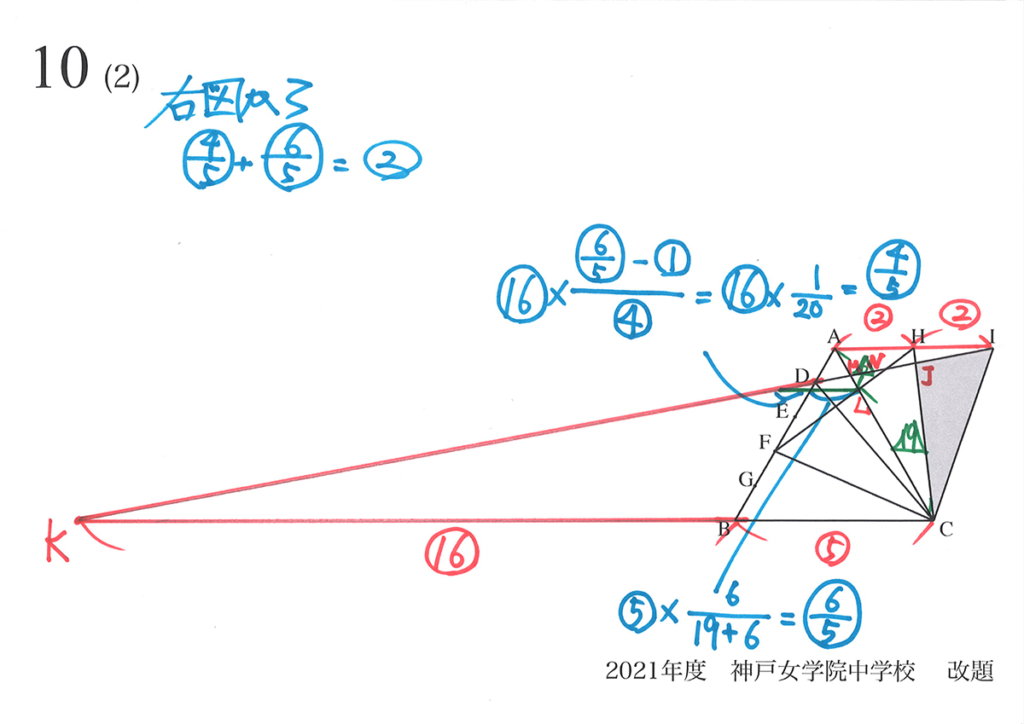
図形問題の補助線と同じで、一番良いのは「自分でやってみる・引いてみる」ことです。
「自分でやってみること」が、学力が上がる最も近道です。
この図形は
この補助線を思いつくようになろう！
と教わって、「補助線のパターン」を覚える学び方もあるでしょう。
確かに、補助線の引き方には「ある程度のパターン」があることが多いです。
それは、「様々試してみて、良い補助線も引いてみて理解する」のが最も良いでしょう。
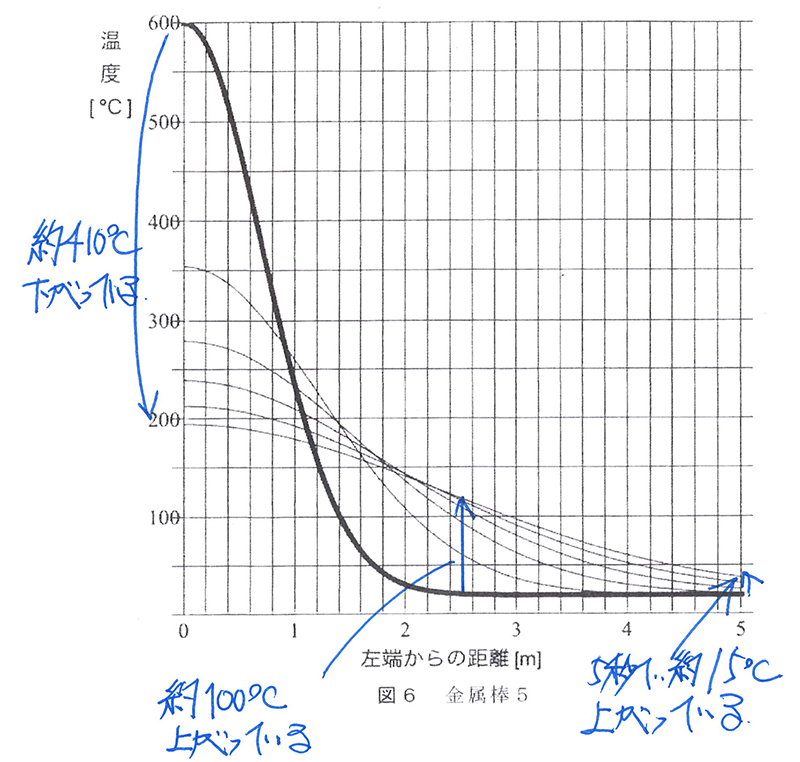
算数・理科・社会、いずれの科目でも「グラフを読んで、理解する」姿勢を作りましょう。
このような姿勢で「しっかり考える」ことが、大事です。
それは「数をこなす」よりも記述式問題に強くなるでしょう。
こういう応用問題は「暗記」ではない「理解力」が試されます。
記述式や応用問題が出題される傾向の志望校受験生は、しっかり理解しましょう。
