前回は「直角二等辺三角形の斜辺・対角線の長さの比較〜問題のヒントを探す・「2回掛けた数字・自乗」を比較・問題 11(4)解法〜」の話でした。
問題11(5)（再掲載）
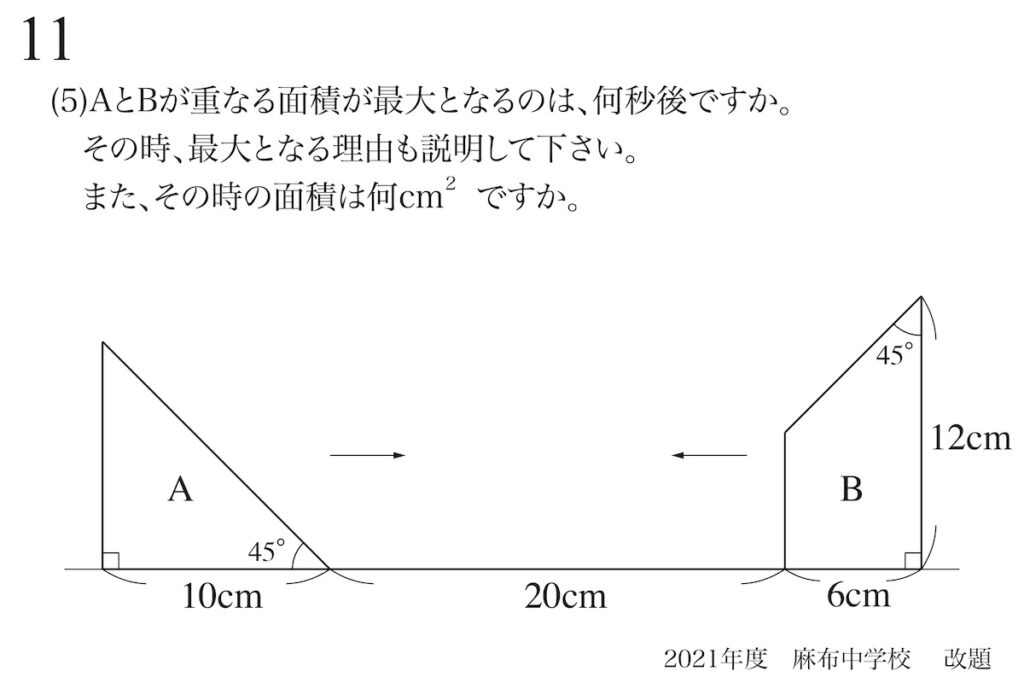
二つの図形が動く時：相対的位置
(2)で「相対的位置」を考えましたが、「二つの図形が動く」ままでも「9秒後の状況」は分かります。
具体的な「〜秒後の状況」は、相対的位置を考えなくても出来ます。
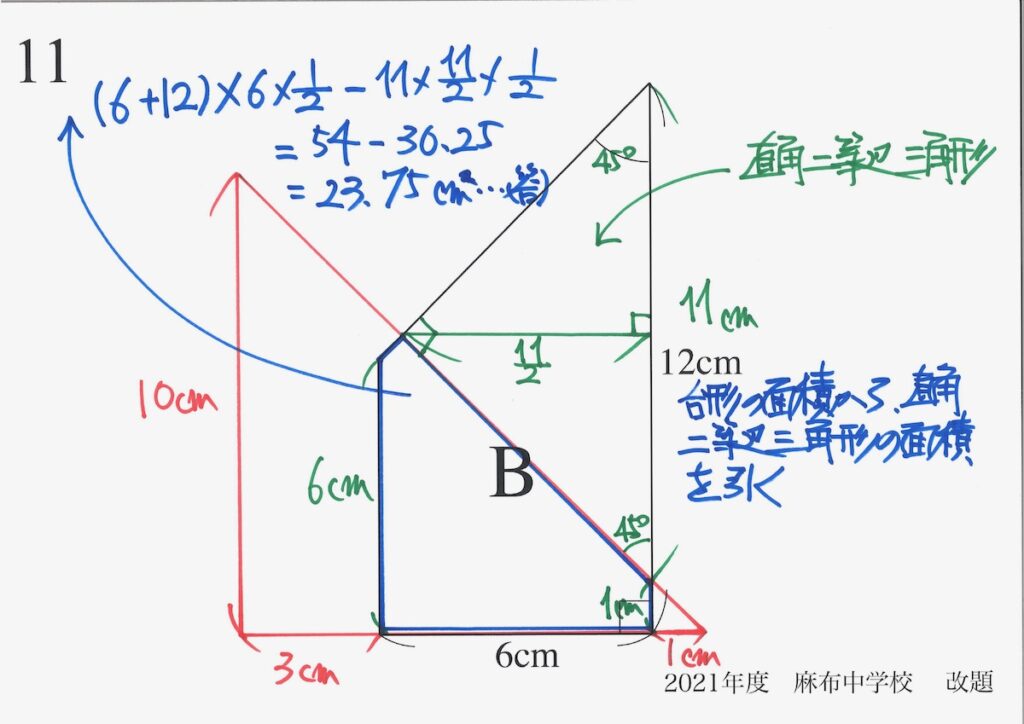
「相対的位置」を考えなくても、「Aが右に〜cm動いて・・・」と考えても解けます。
(5)のように「重なる面積が最大」となると、「二つが動く状況」は非常に考えにくいです。
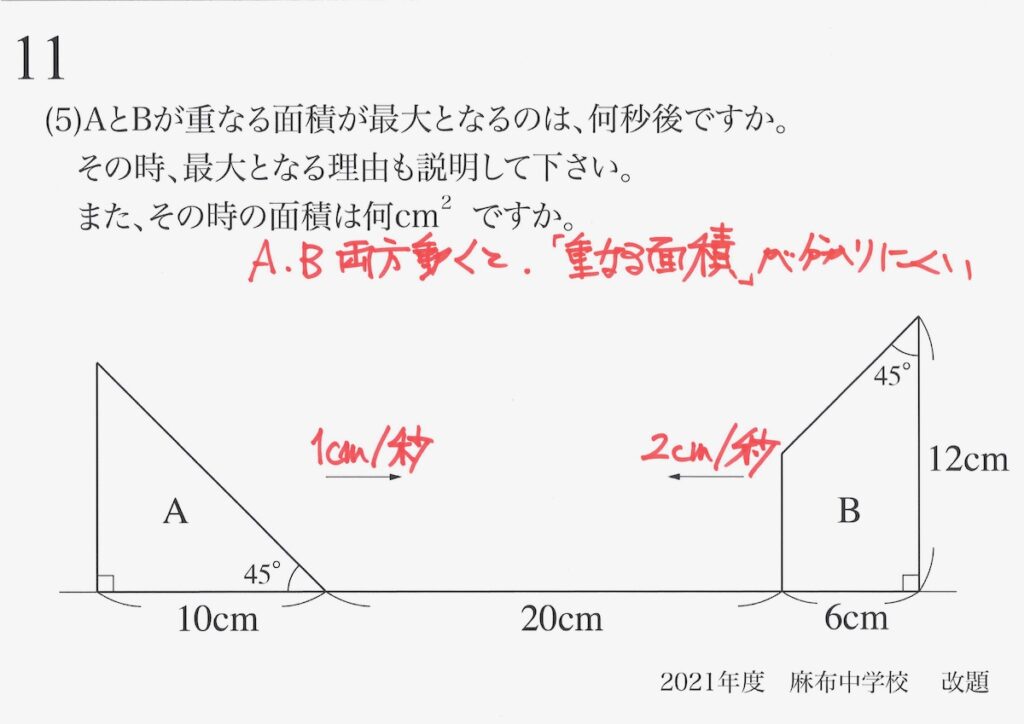
(2)と同様に「相対的位置」を考えて、「BにAが3cm/秒の速さで向かってくる」状況を考えましょう。
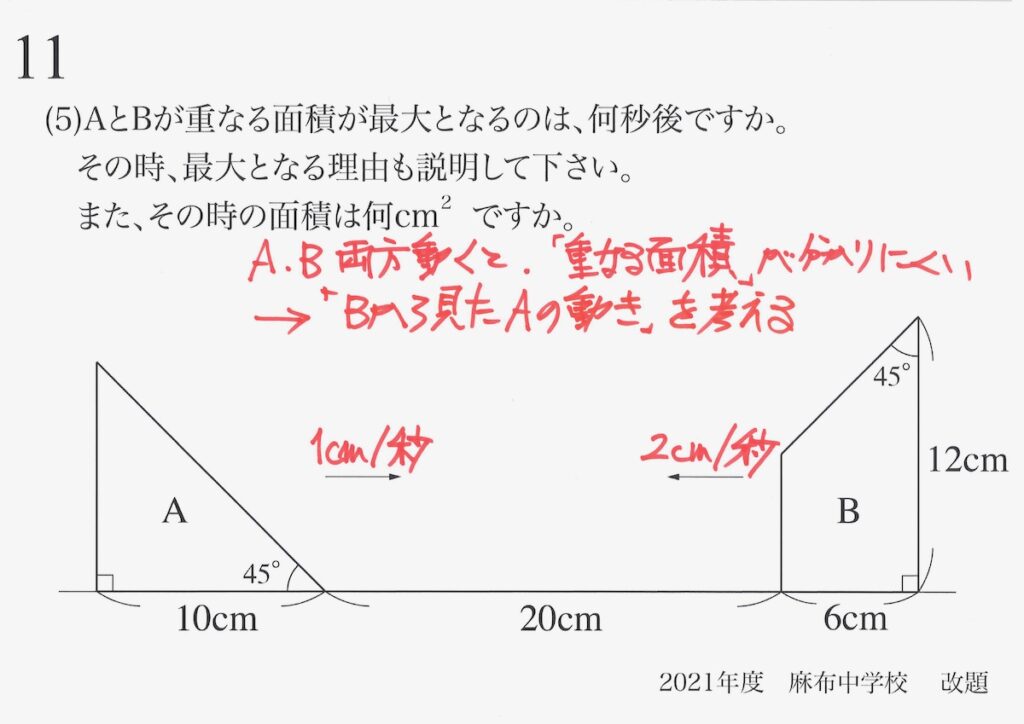
この時、逆の「AにBが3cm/秒の速さで向かってくる」を考えても同じです。
「相対的」ということは、「逆を考えても同じ」なので自分が好きな方で考えましょう。
重なる面積の形を追いかける
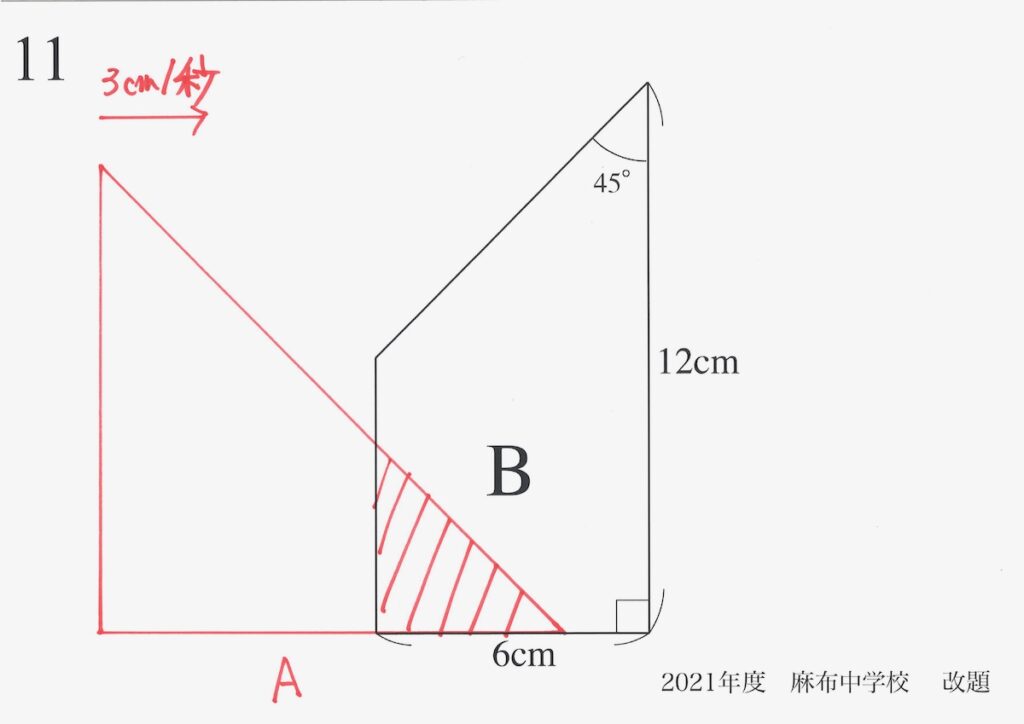
AとBが接してから、重なる面積がどうなるか描いてみましょう。
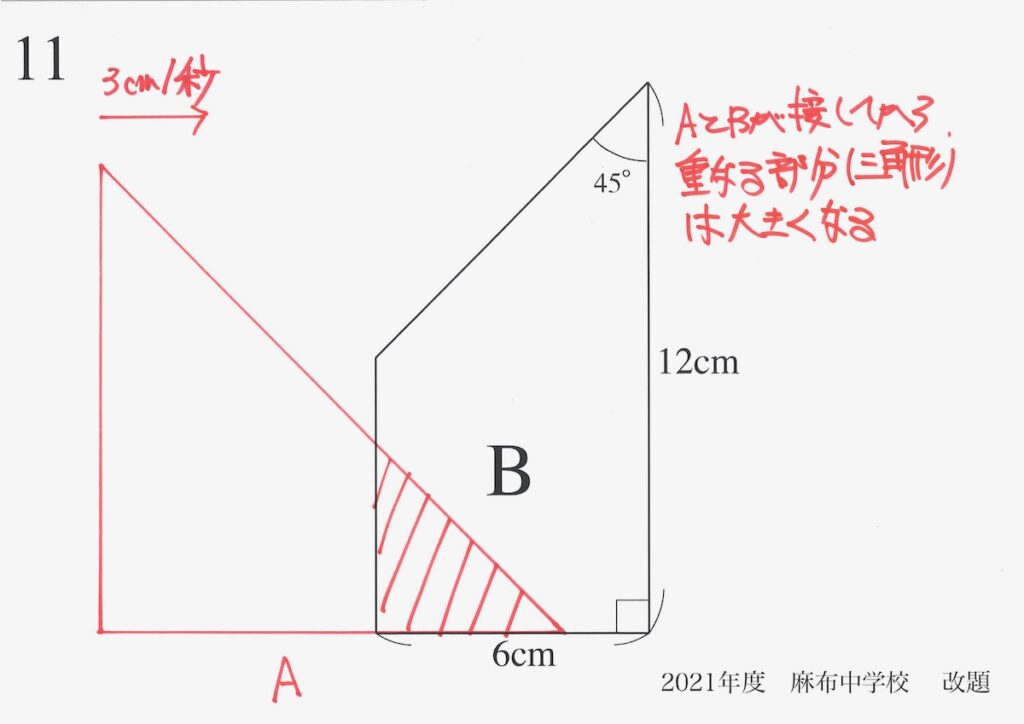
重なる部分は、直角二等辺三角形になって、しばらく大きくなります。
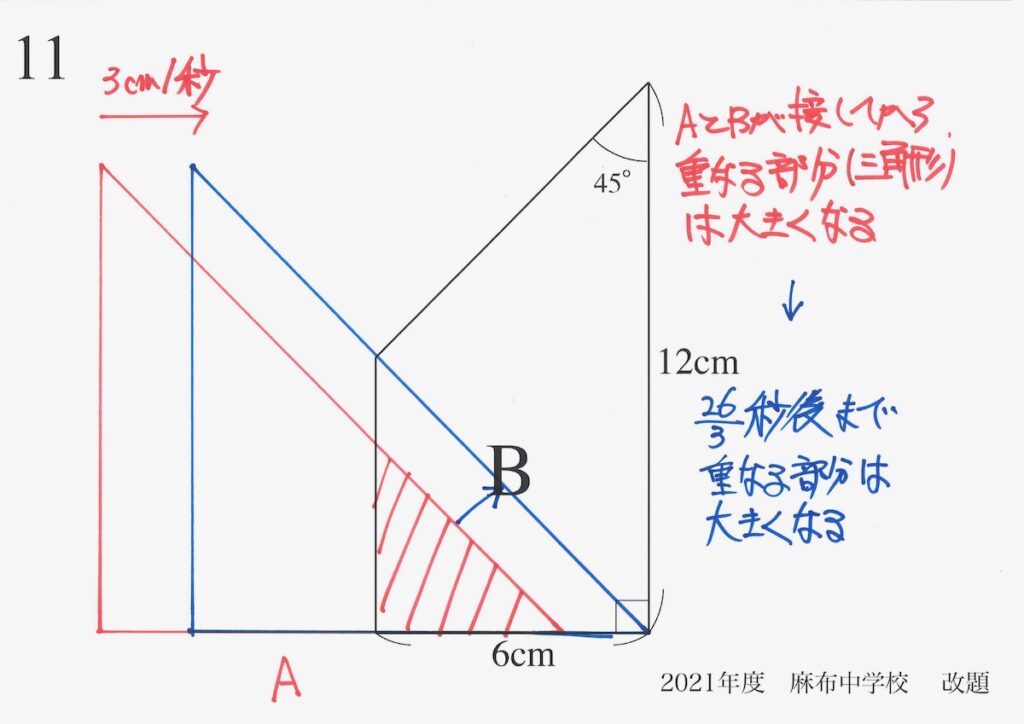
どこまで、「似た状況が続く」か考えましょう。
男子小学生Aの右下の角がBの直角になるまで、
重なる部分は直角二等辺三角形だね！
女子小学生それまでの
時間を考えればいいね！
26/3秒後までは、重なる部分・面積は大きくなってゆきます。
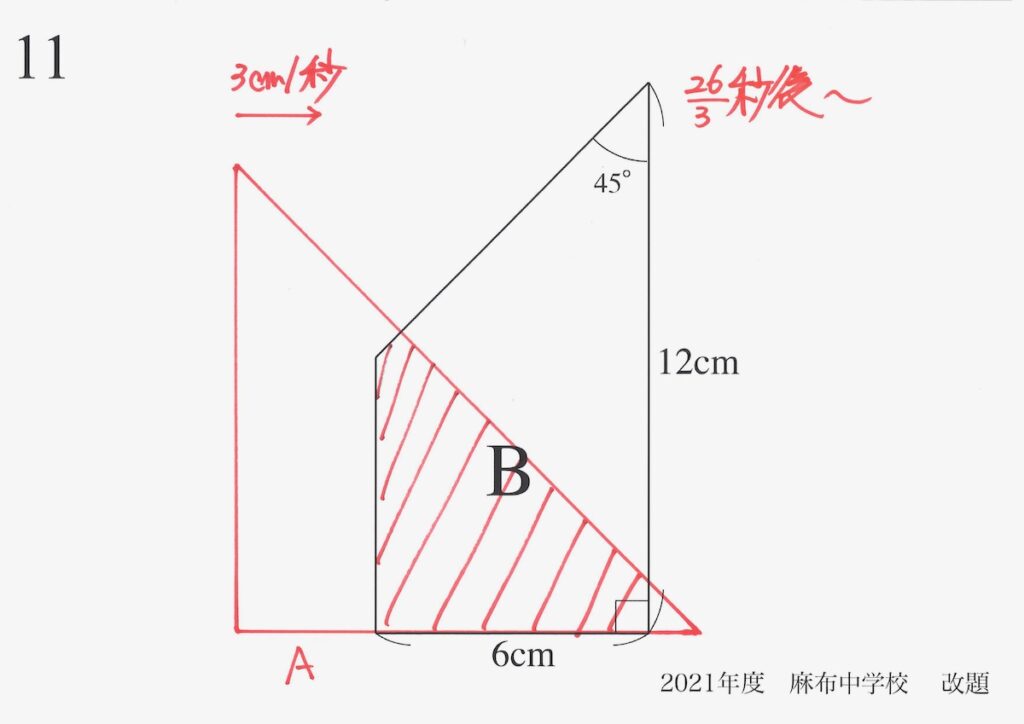
その後は、(2)で考えた状況に近くなります。
男子小学生ここは、(2)と
同じように考えられそう！
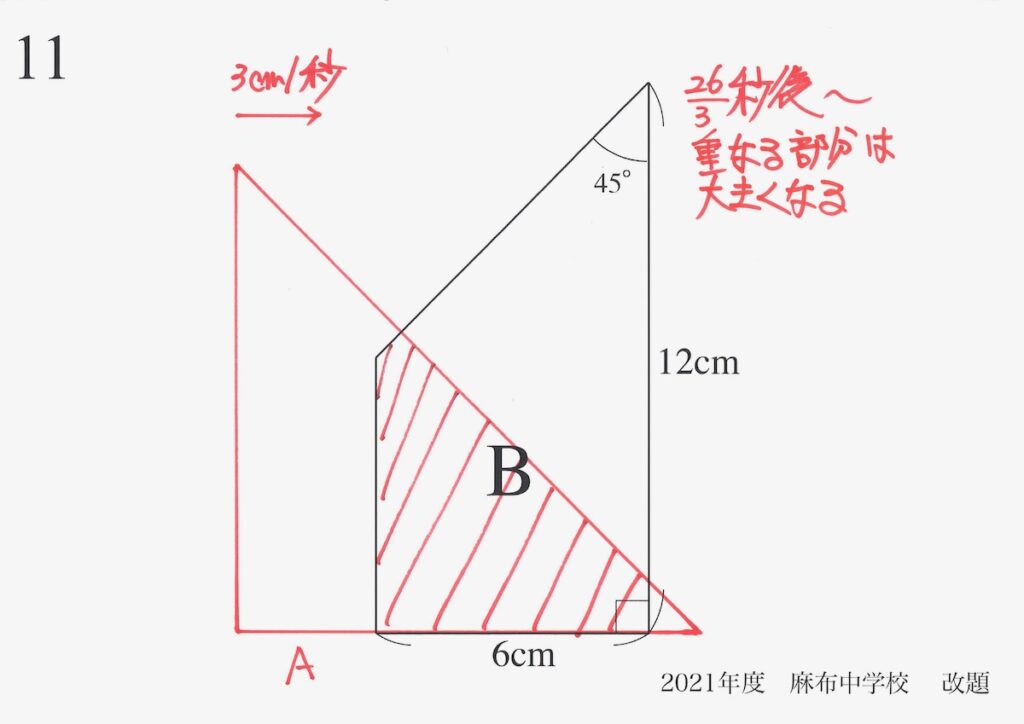
女子小学生重なる部分が増えるから、
面積も増えるね！
男子小学生少しずつ、重なる部分が
増えていく感じだね。
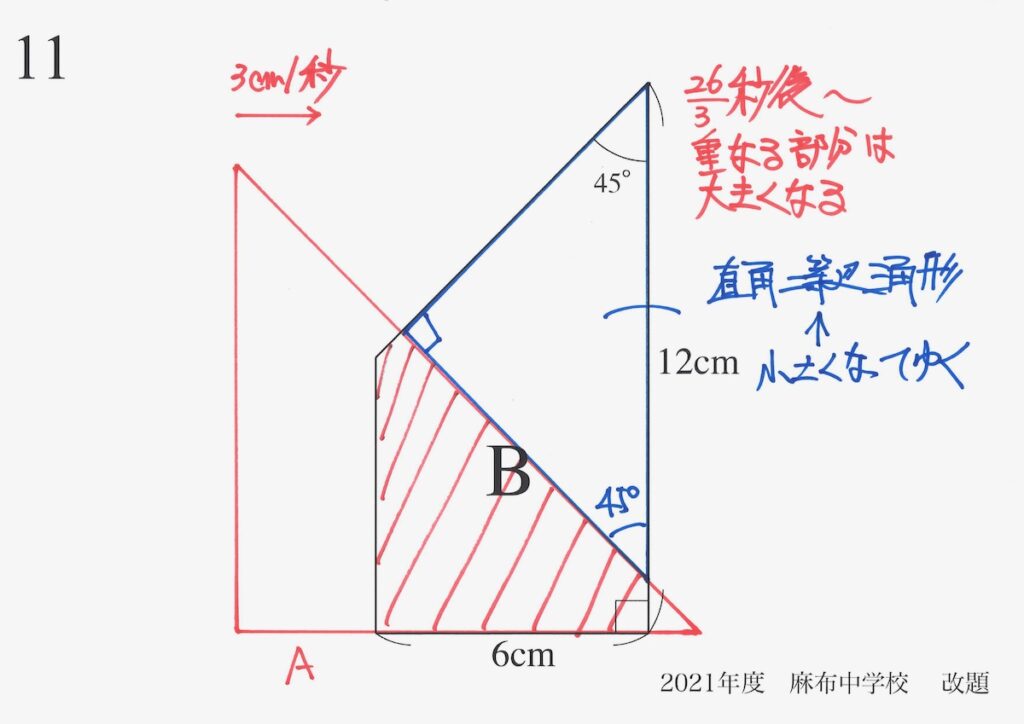
「重なる部分の面積=B（台形の面積）-青色の直角二等辺三角形」と考えてみましょう。
女子小学生Bのうち、重なっていない部分は
青色の直角二等辺三角形だね！
男子小学生こっちの青色の直角二等辺三角形は
小さくなっていくね！
女子小学生「重なっていない部分の面積」が小さくなっていくから、
「重なった部分の面積」は増えていくね！
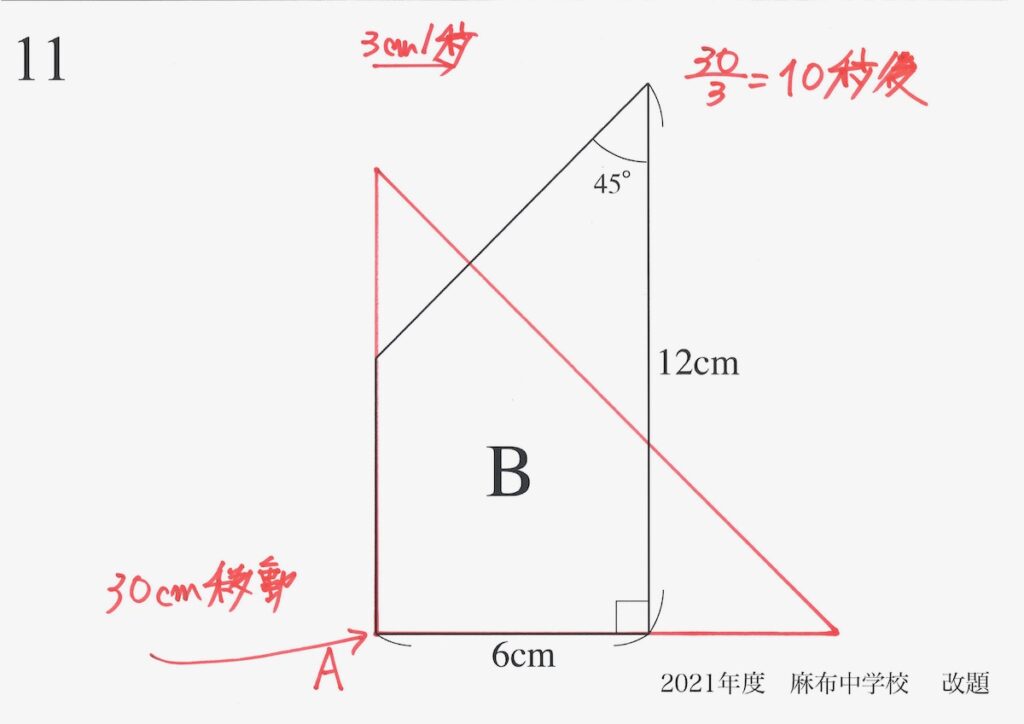
10秒後には、上のような状況になります。
ここまで、重なる部分・面積が大きくなるのは、図を描いて「明らか」として良いでしょう。
少し動かして考える：増える面積と減る面積
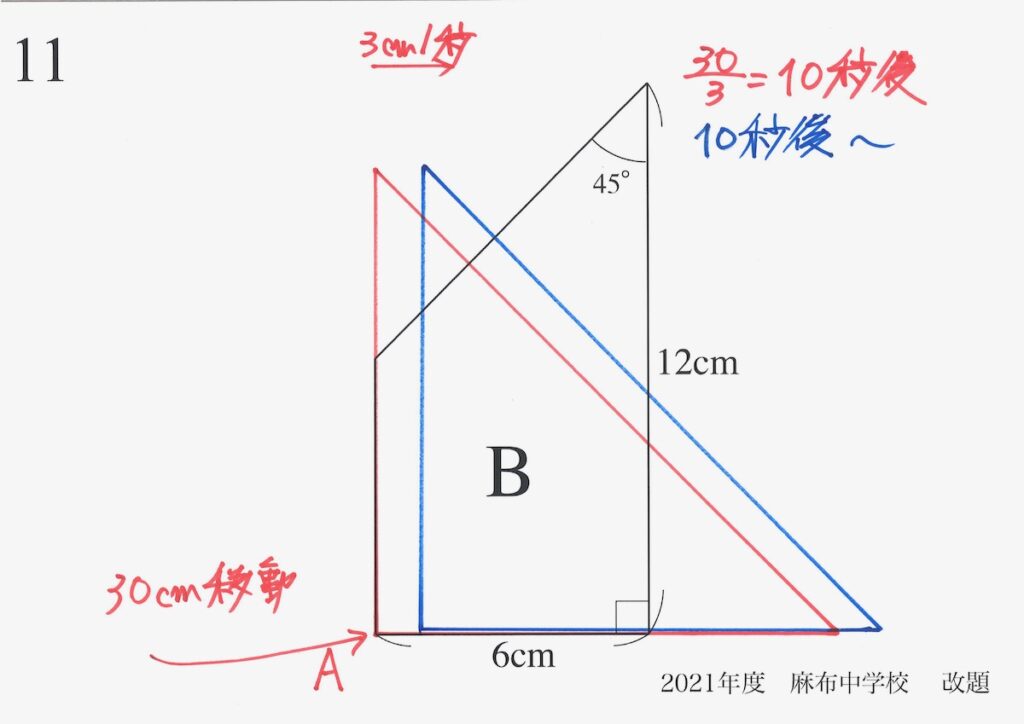
この後、少しAを右に動かしてみましょう。
男子小学生ここからは
少し難しそう・・・
重なる部分がだいぶ大きくなった10秒後から、Aは赤から、青に移動します。
ずっと大きくなり続けた重なる部分の面積をどう考えるか、が問題です。
男子小学生ちょっと小さくなった
気がする・・・
女子小学生赤の時が
一番大きいかな・・・
中学以降の数学であれば、面積を立式して具体的に分かります。
算数の範囲では面積の立式は少し難しいので、「面積がどうなるか？」を考えましょう。
図を見た感じでは、10秒後の赤の状況が「重なる部分が一番大きい」感じがします。
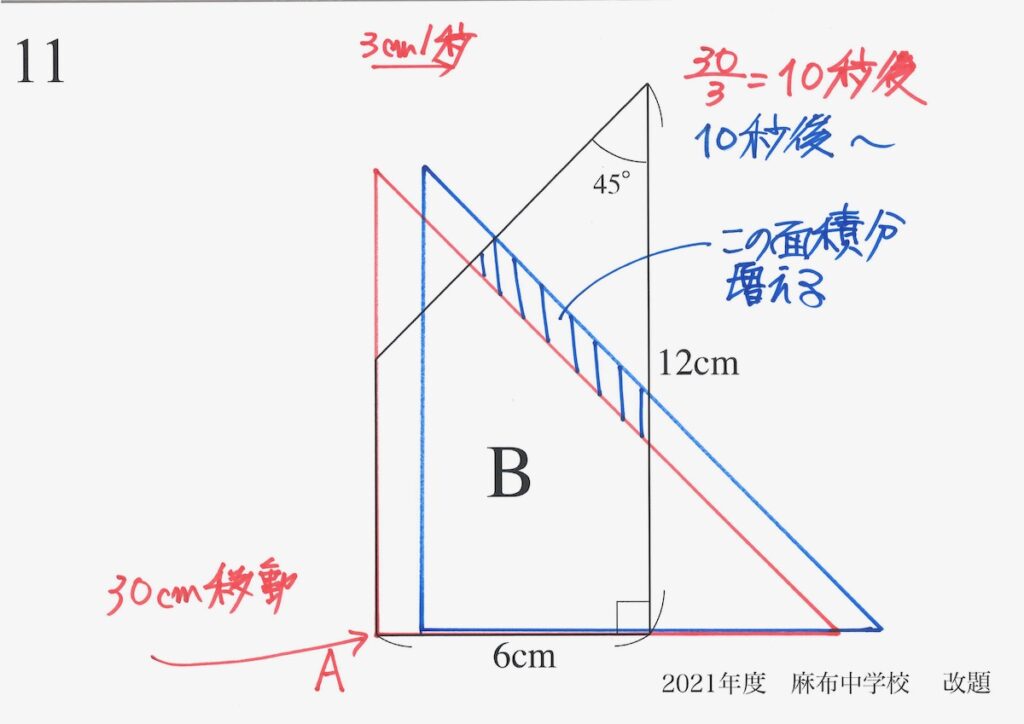
重なる部分の「増える部分・面積」と「減る部分・面積」を考えましょう。
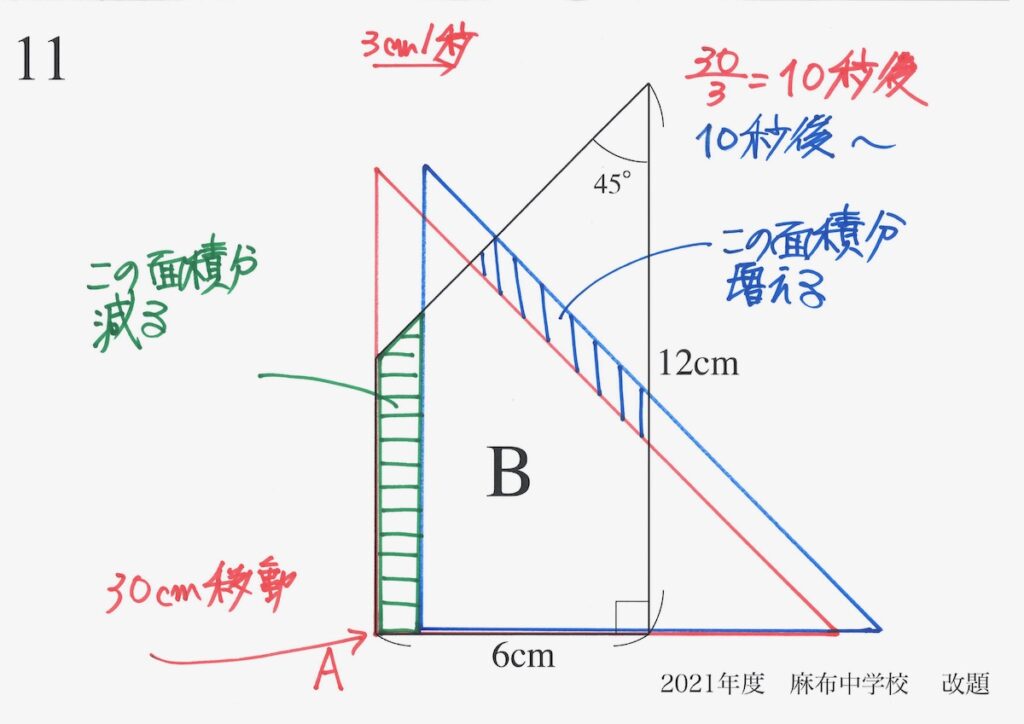
「増える面積」と「減る面積」を描いて、比較してみましょう。
「減る面積」の方が、少し大きそうです。
男子小学生確かに
そんな気がするけど・・・
女子小学生どうみても、
緑の「減る面積」の方が小さいけど・・・
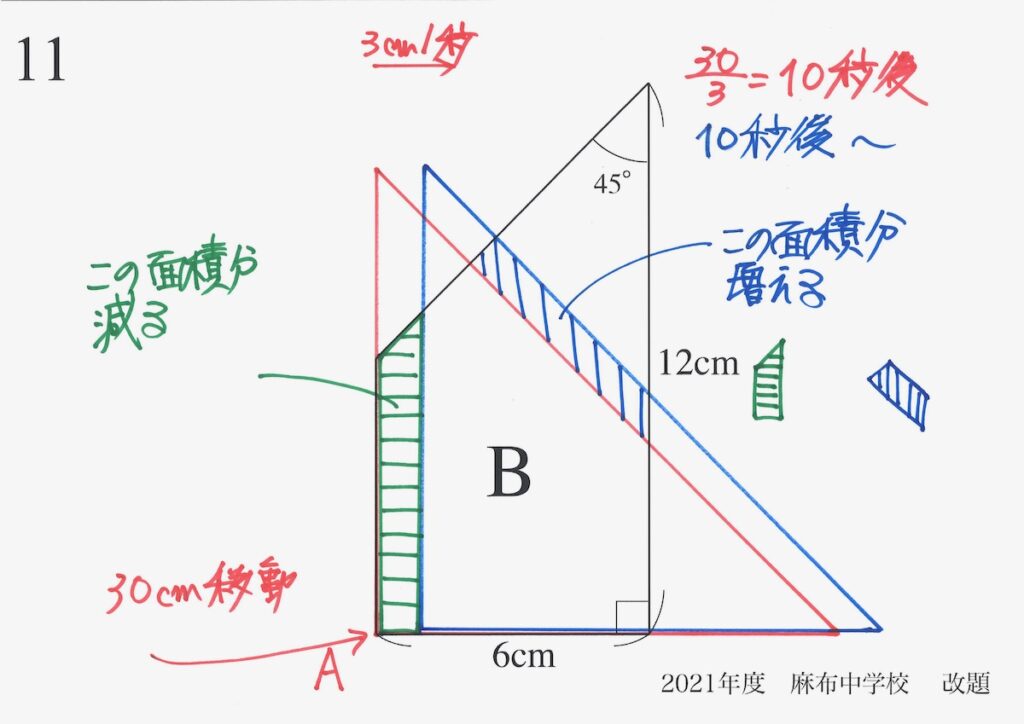
「減る面積の方が大きい」が分かれば、「赤の時が、重なる部分・面積が最大」と分かります。
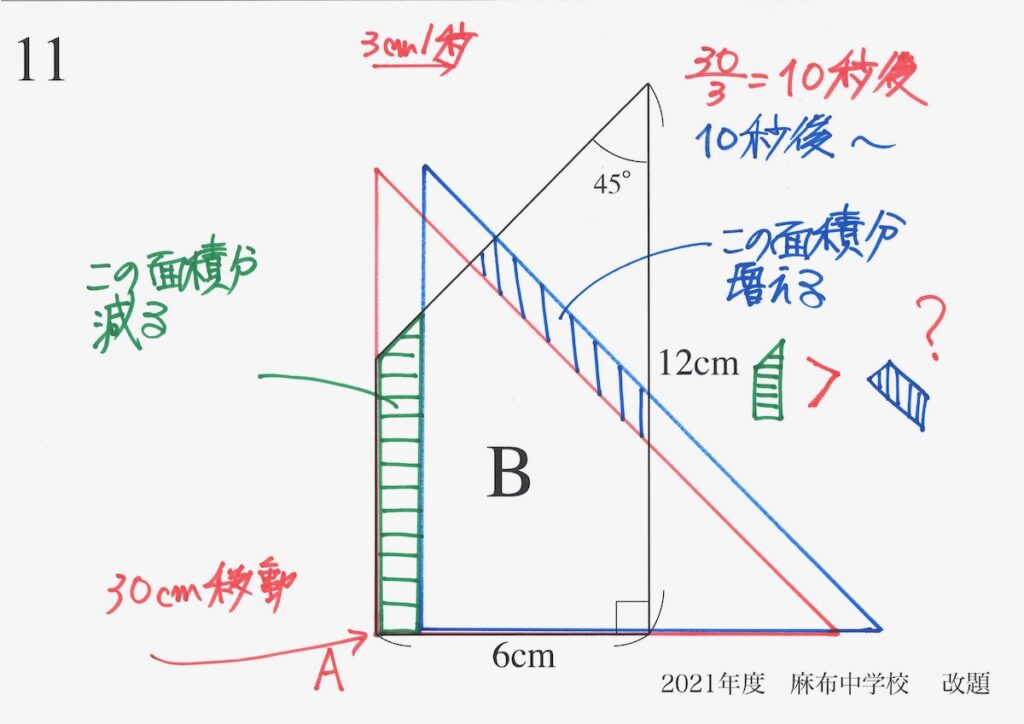
上の図で、「青色の部分 > 緑色の部分」を示すことを考えてみましょう。
算数実践 57（上のリンク）で「長さ」を考えましたが、同じように「面積」の大小を考えてみましょう。
次回は下記リンクです。
