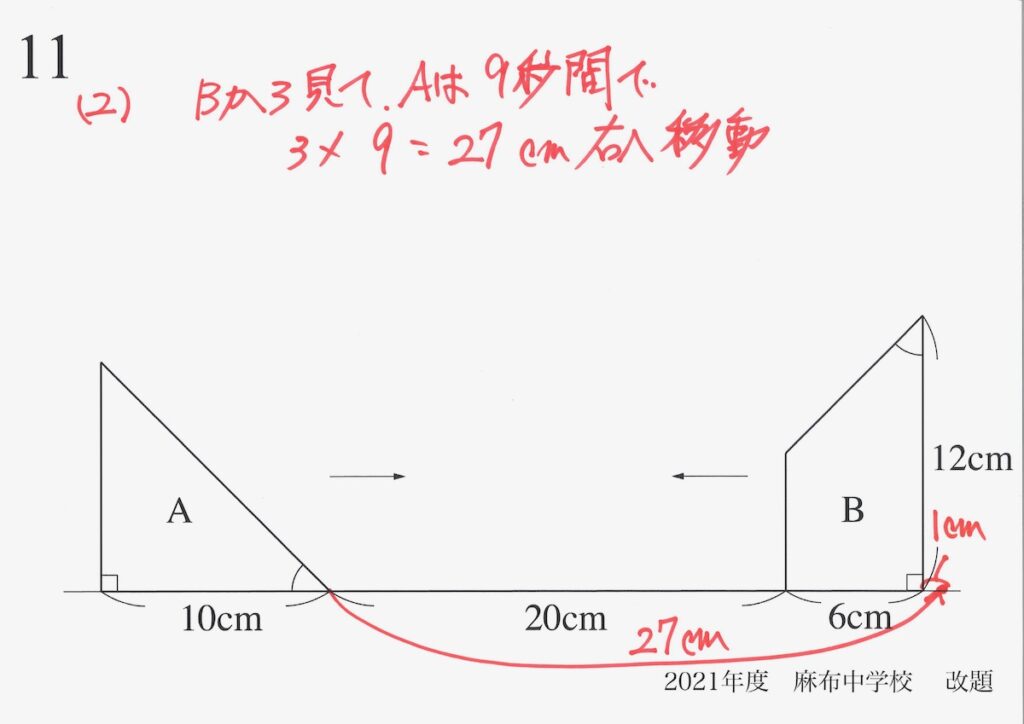
前回は「重なる図形の面積が分かるポイント・コツ〜重なる図形を描く・片方の図形に対する速さ・「直角・同じ長さ」など図形の特徴を把握・問題11(2)解法〜」の話でした。
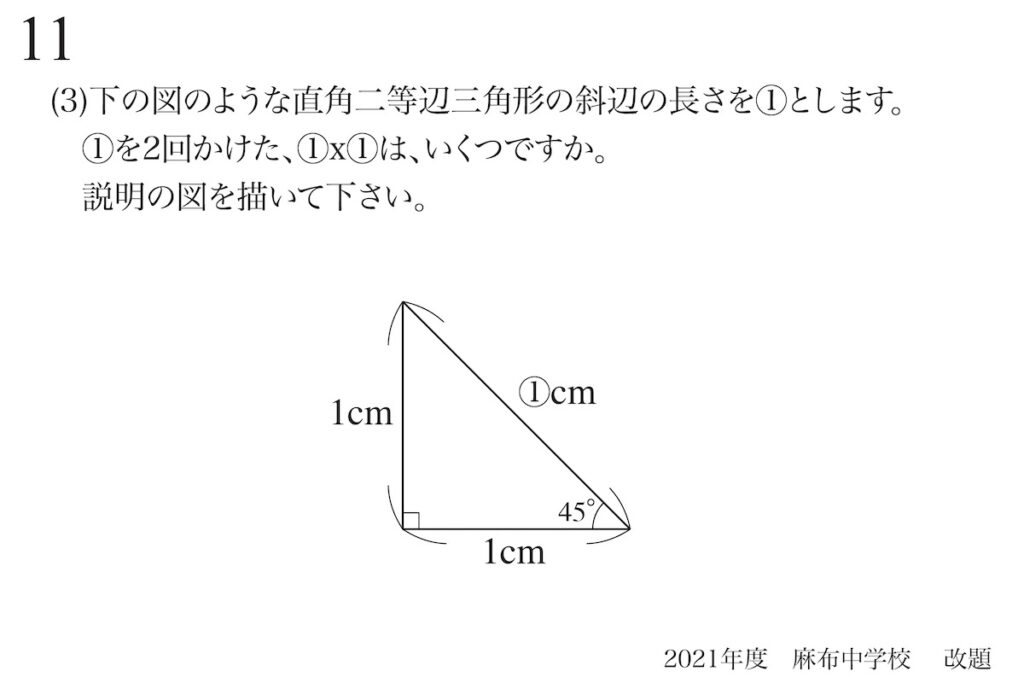
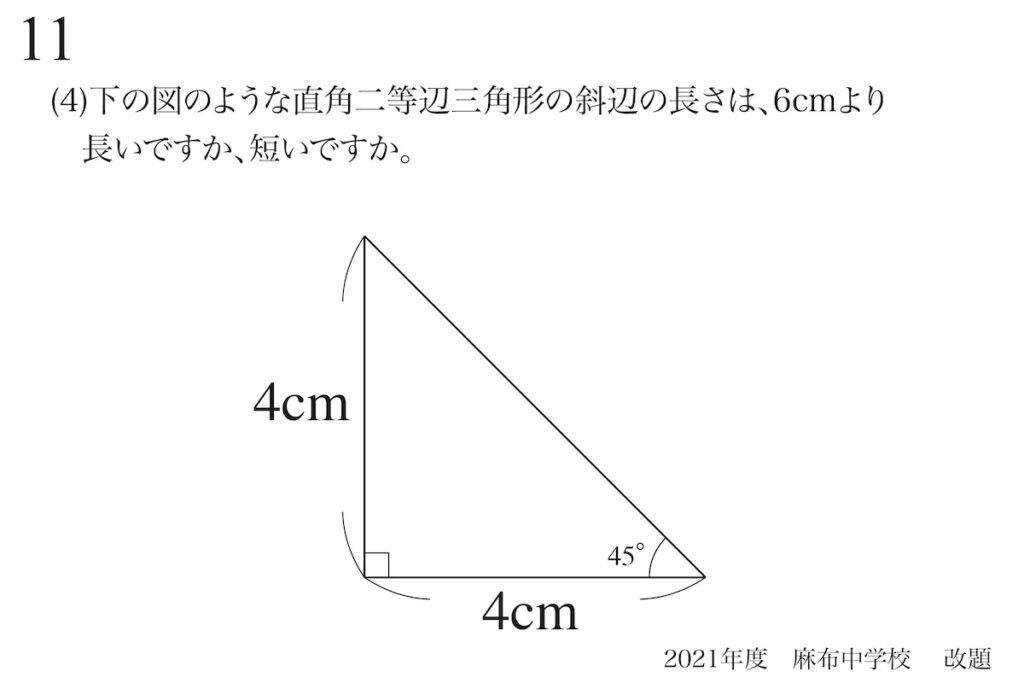
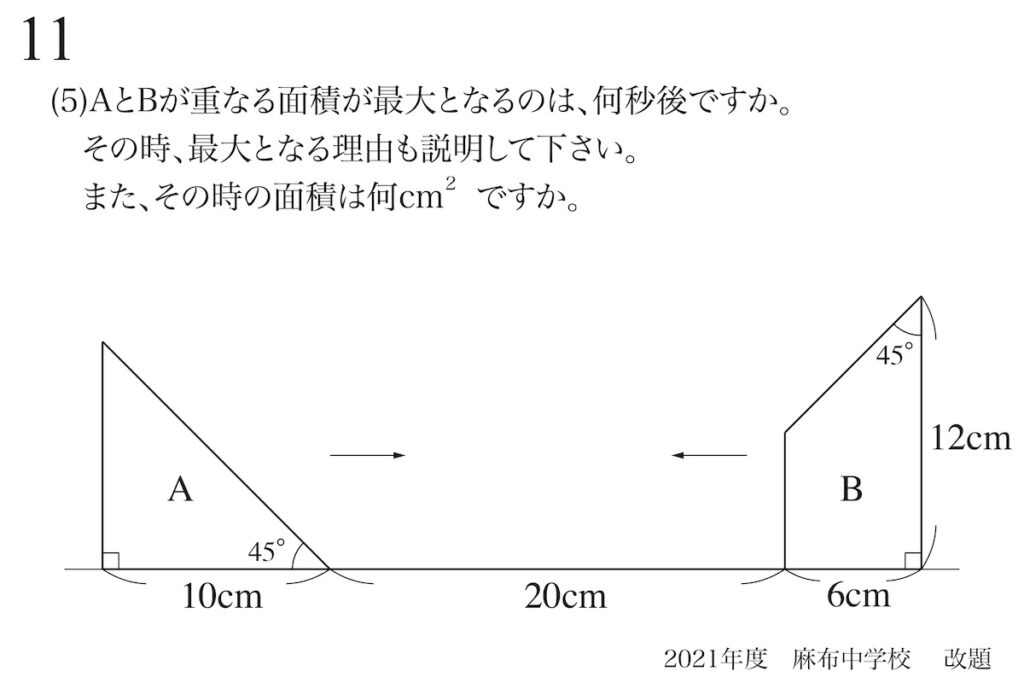
問題11(3)(4)(5)
直角二等辺三角形の性質:正方形と直角二等辺三角形
今回は(3)〜(5)の出題です。
(3)(4)は少し問題から離れますが、(5)につながります。
・元の図形の特徴を把握
・元の図形の中にある「正方形・正三角形・直角二等辺三角形」など特徴的図形を発見
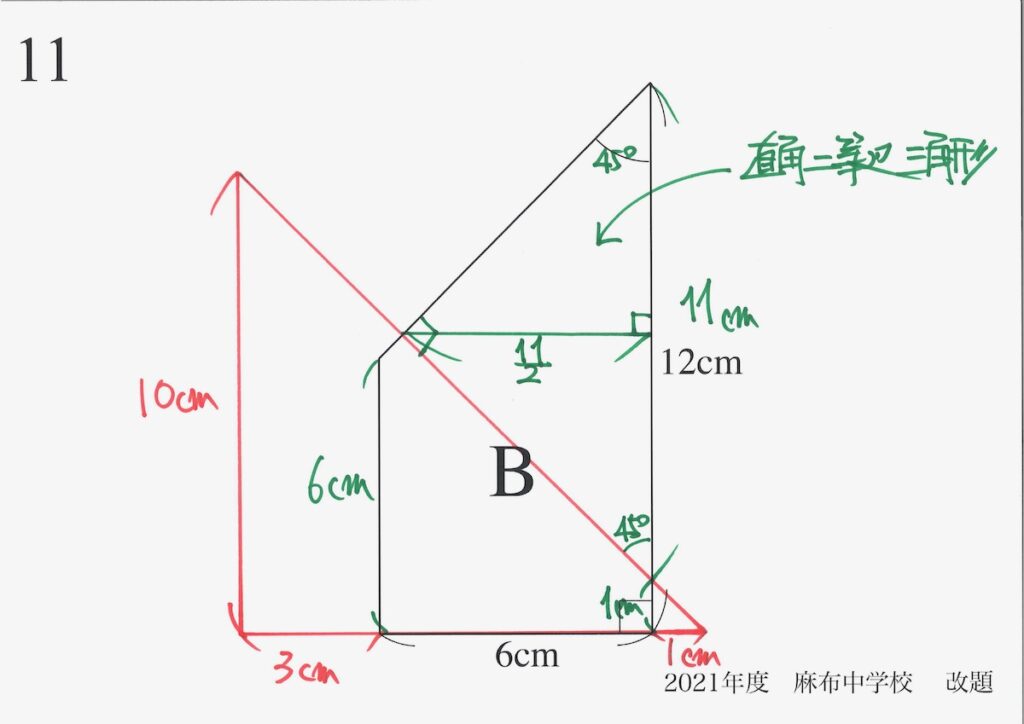
今回動く図形は、両方とも「直角二等辺三角形がポイント」です。

小学校2〜3年生くらいから使う「一組の三角定規」は、「直角二等辺三角形」と「正三角形の半分」です。
 女子小学生
女子小学生三角定規のセットは、
角度の問題もあるね!
これらの二つの三角定規を組み合わせて、角度を問う問題も算数ではよく見かけます。
直角二等辺三角形は、比較的馴染み深い三角形です。
正方形に斜辺を入れると、直角二等辺三角形が登場します。


方眼紙で工作する時、「斜めに切る」と直角二等辺三角形がたくさん登場します。



確かに工作の時は、
直角二等辺三角形が、よく出てくるね!
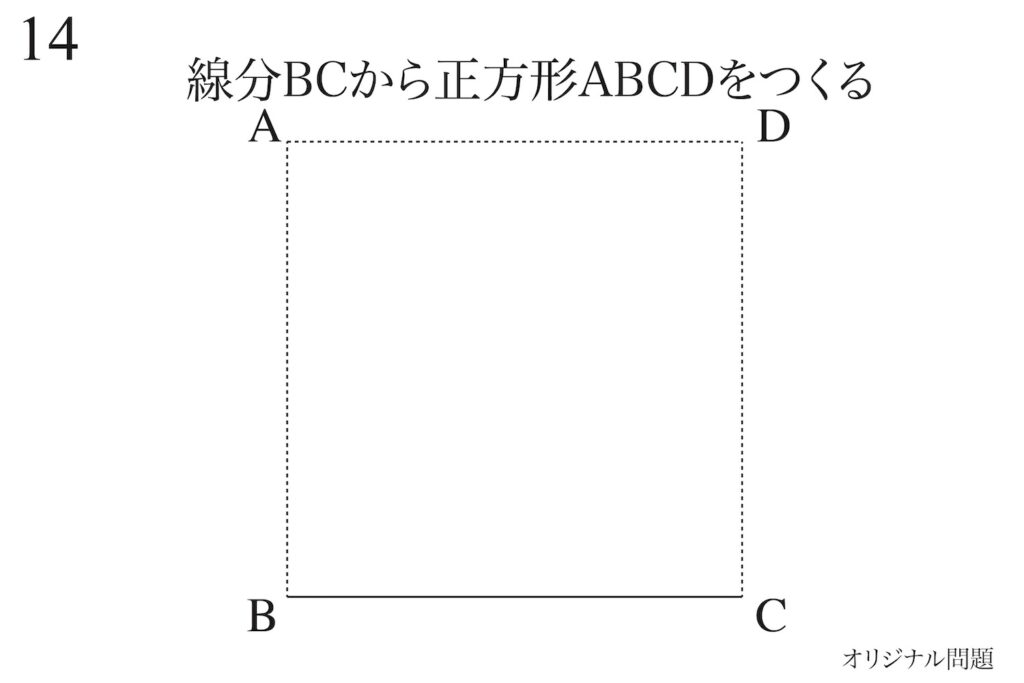

正方形の作り方を復習しましょう。
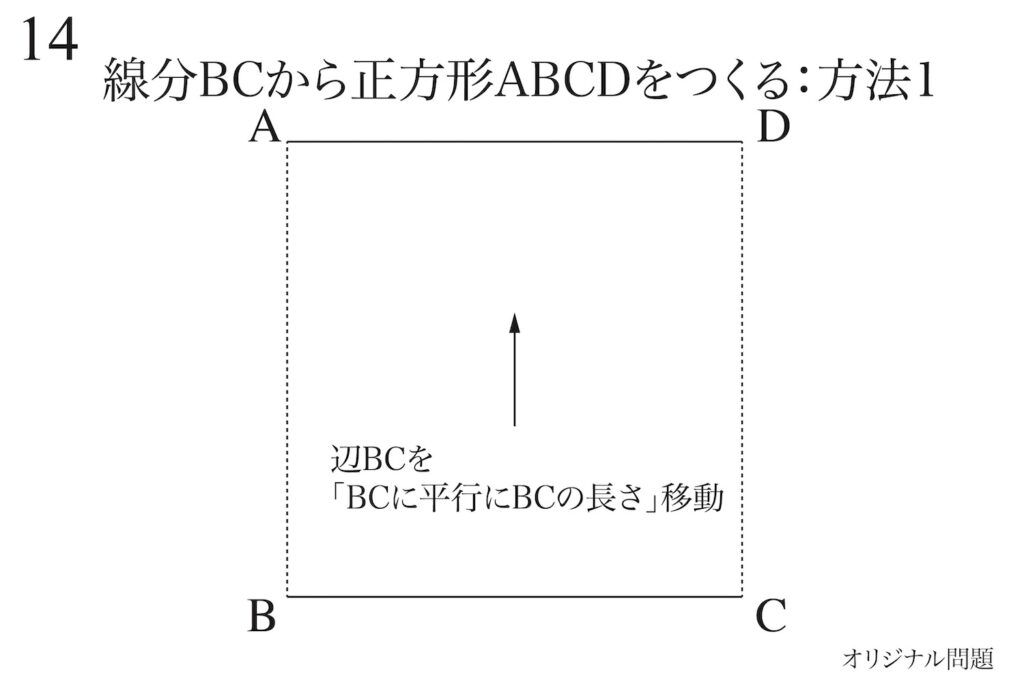

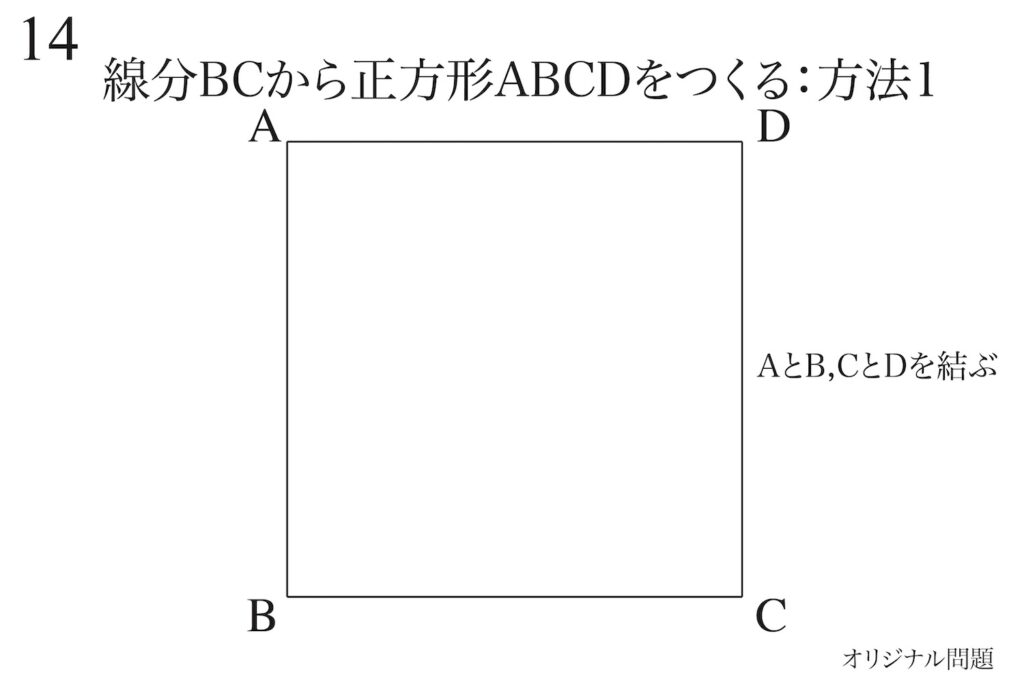

一辺を「その辺と同じ長さ」平行移動すれば、正方形を作ることができます。
もう一つ「正方形の作り方」を考えましょう。
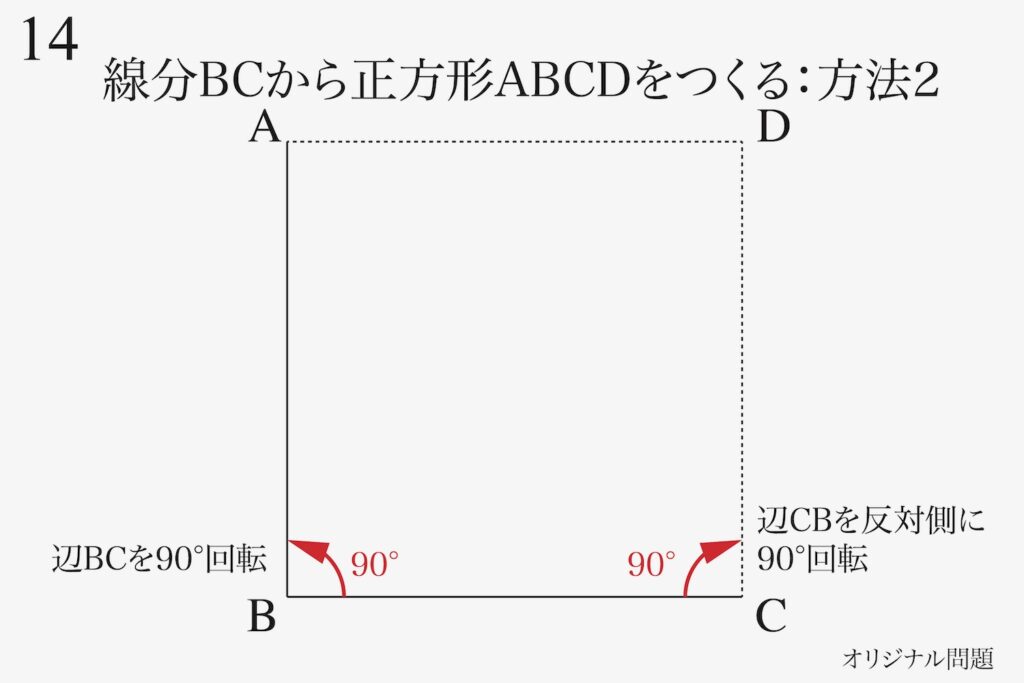

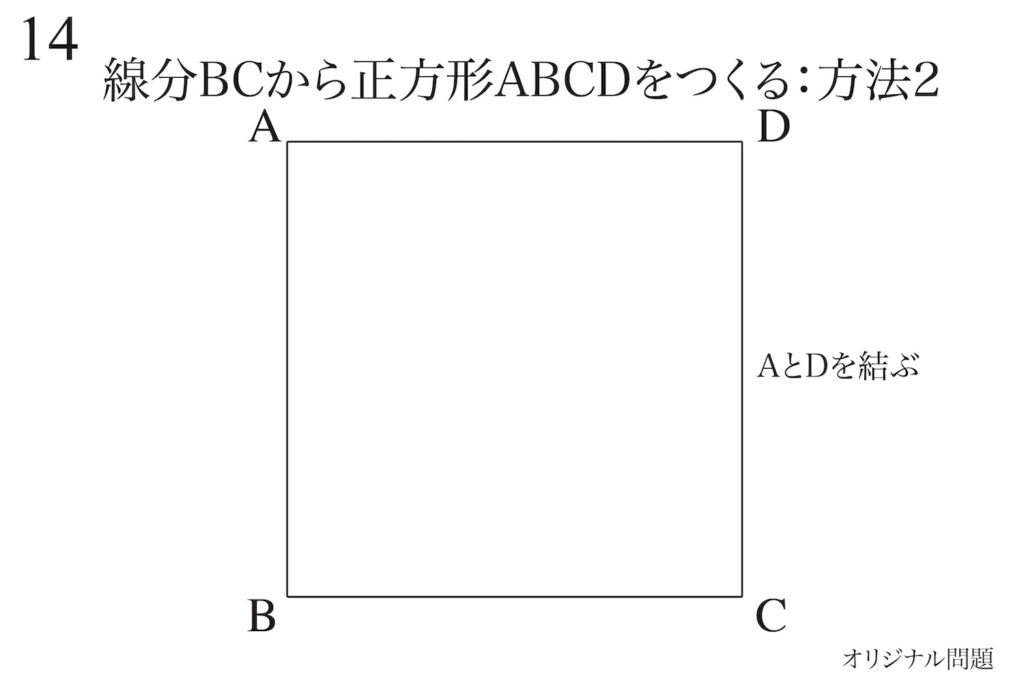

「辺を90度、反対側に90度回転する」と正方形が作れます。
・全ての辺が同じ長さの四角形
・全ての角が同じで直角の四角形
直角二等辺三角形は、正方形を「斜めに半分」した図形なので、正方形と特徴が似ています。
・直角を挟む辺の長さが同じ三角形
・直角以外の角度は45度(直角の半分)の三角形
とても分かりやすい直角二等辺三角形ですが、「斜辺の長さ」は算数では分かりません。
中学以降の数学で習いますが、今回は「斜辺の大体の長さ」を考えます。
図形の性質と最大・最小の面積
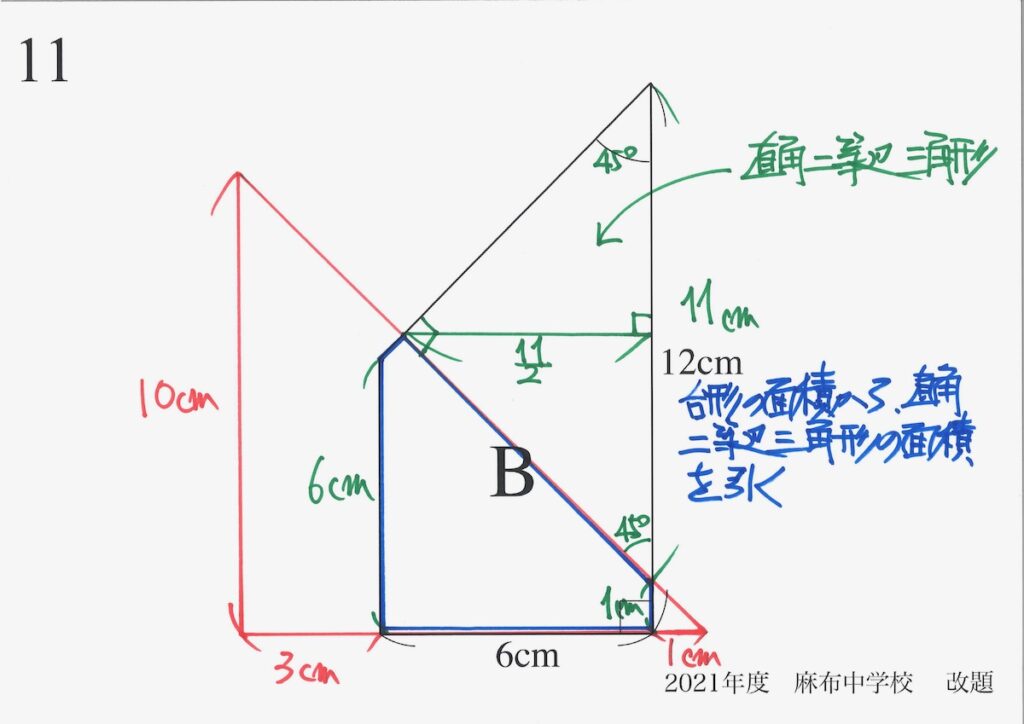

図形の面積の最大・最小を考えるときは、「どのように面積を計算するか」で考え方が変わります。
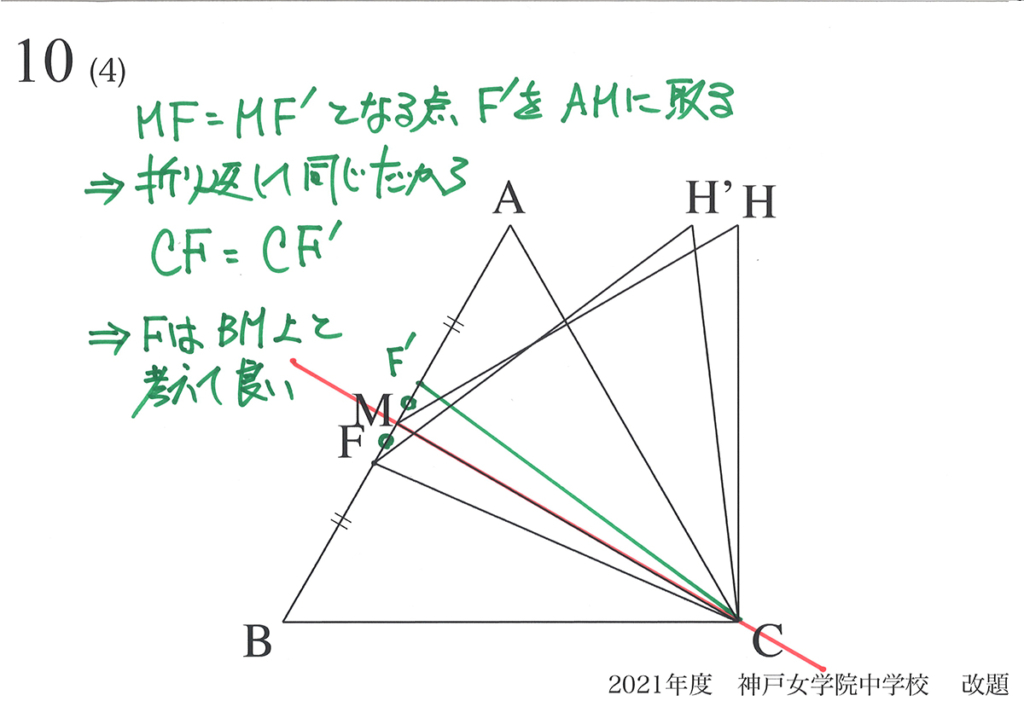

「面積の最大となる」時を考えるのは、基本的には中学以降の数学的内容になります。
算数実践56でご紹介(上記リンク)しているように「予想して、説明する」算数的考え方で考えてみましょう。
少し難易度が上がるので、出来なかった方は解法を読んで、理解して頂ければと思います。
次回は下記リンクです。


