前回は「二つの移動する図形が分かるポイント・コツ〜相対的位置・「変化しない量」は大事なポイント・問題11(2)解法〜」の話でした。
問題11(再掲載)
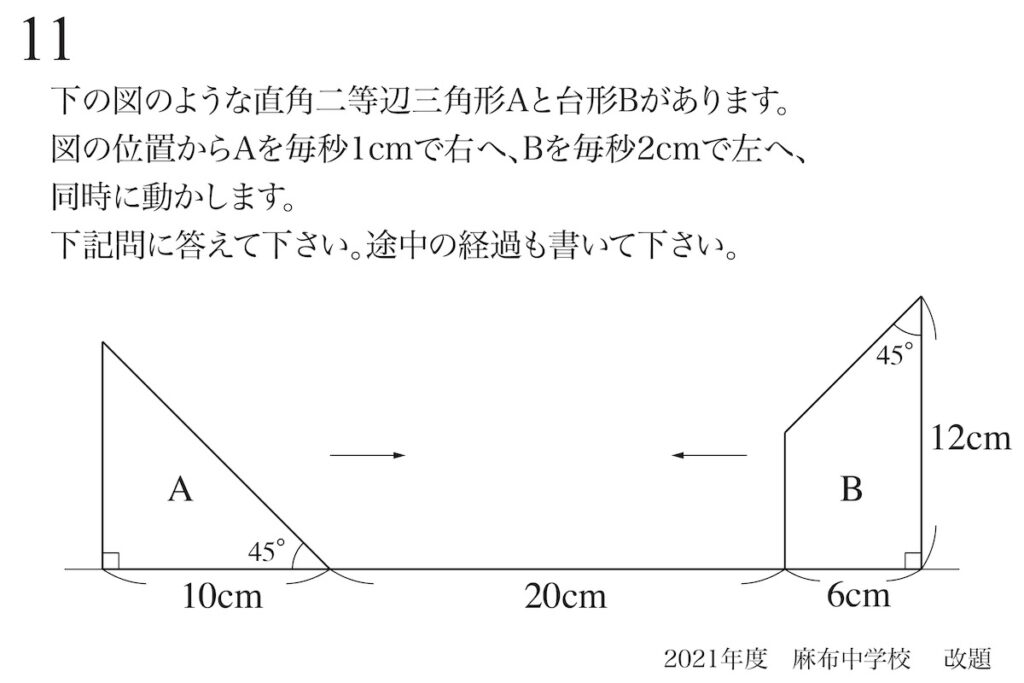
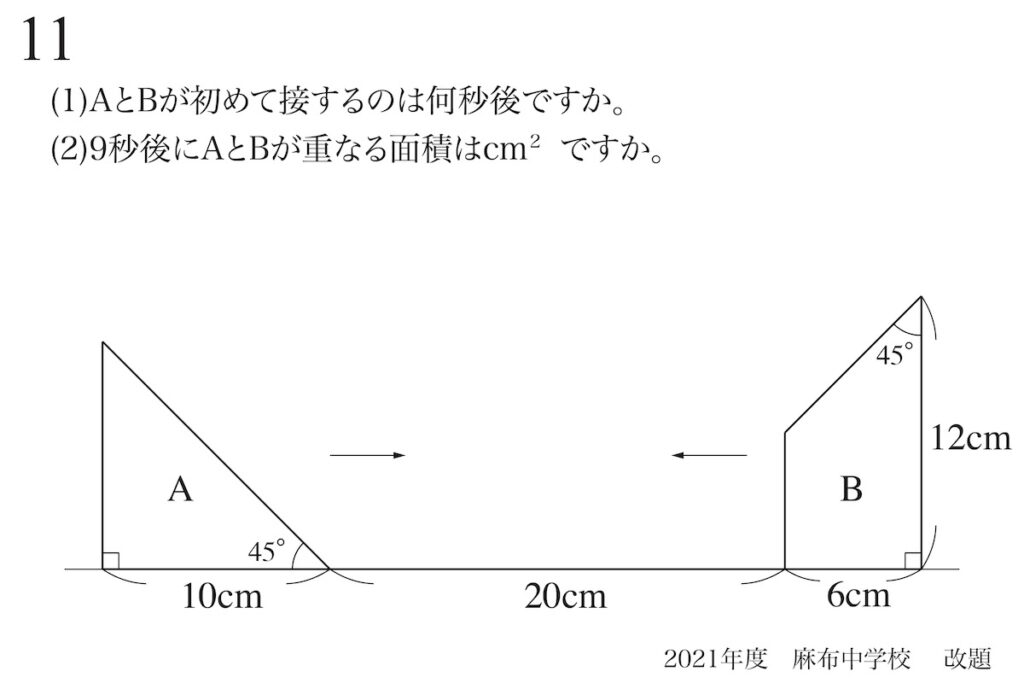
重なる図形を描く:片方の図形に対する速さ
求めるのは面積ですが、「重なる図形」をしっかり押さえることが大事です。
図形が動いたり、回転したりする問題は、まず「動いた後」や「回転した後」の状況の把握が大事です。
「回転した図形」の解くコツを上記リンクでご紹介しています。
対して、「動く図形」の場合は、「動いた後」の図形が描かれていないことが多いです。
 男子小学生
男子小学生確かに、回転する図形は
問題文と一緒に図形が描かれていることが多いね・・・



「動く図形」は問題文で「動いた後」が
描かれていることは、あまりないね・・・
そこで、「動いた後」の状況をしっかり理解して、描くことが大事です。
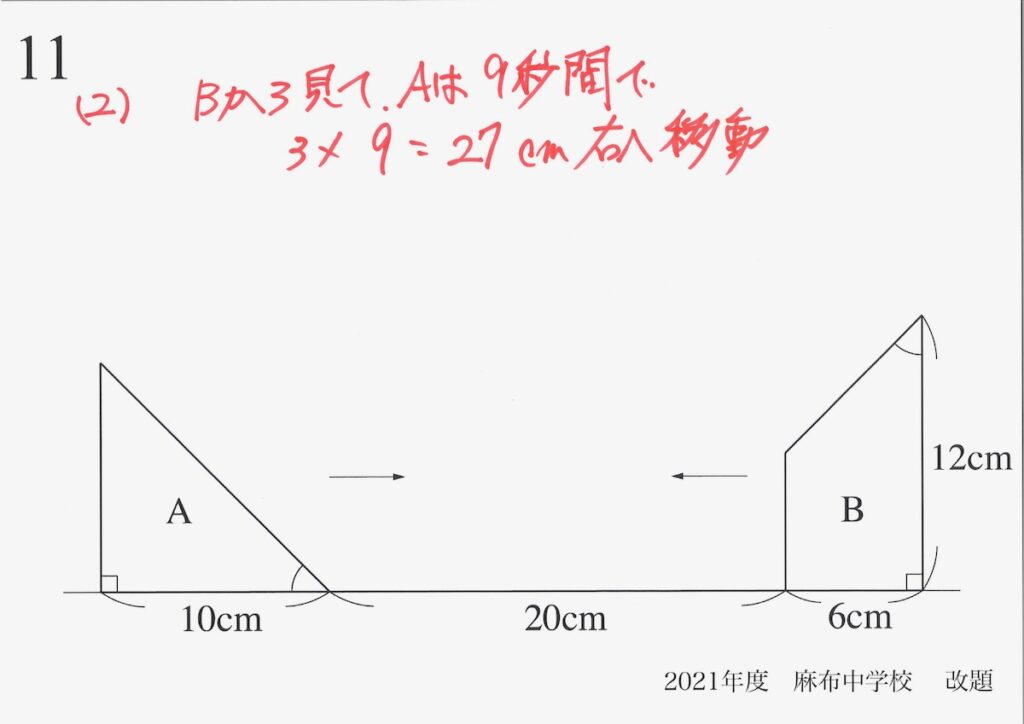

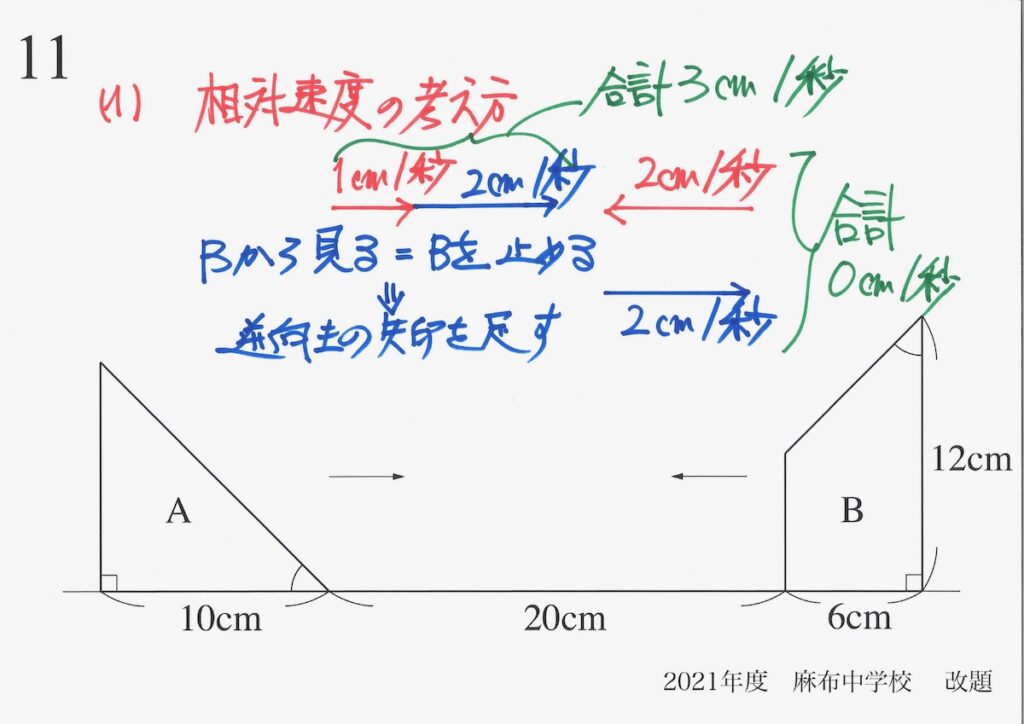
ここでは、相対的速さを考えて、「Bから見て、Aが27cm右へ移動する」と考えましょう。
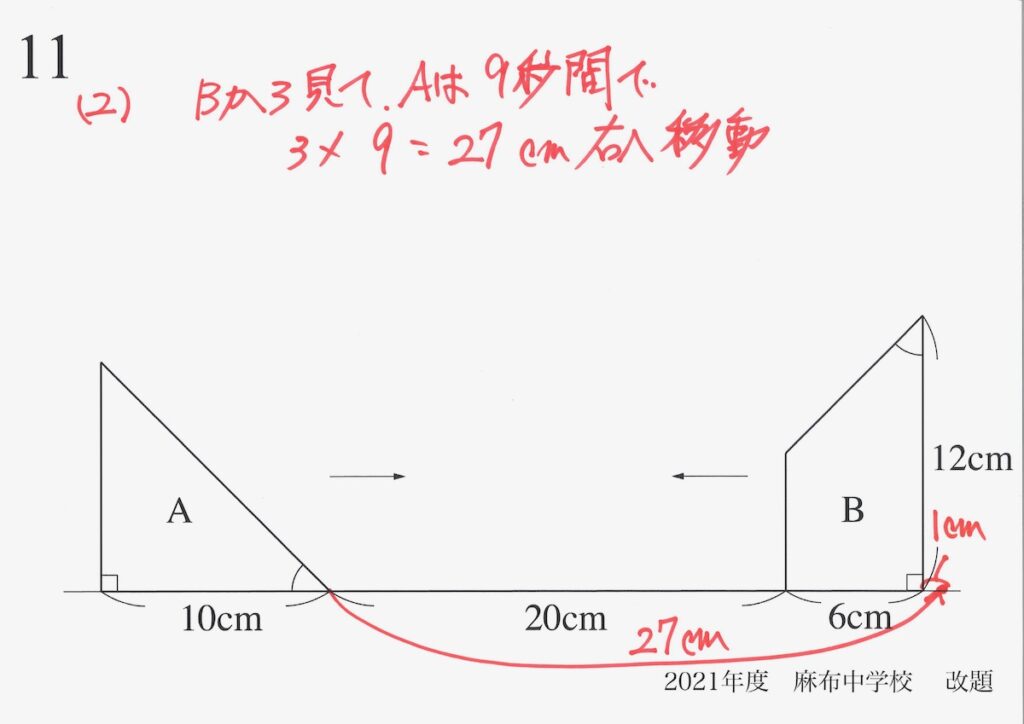

上のような状況を「しっかり描いてみる」ようにしましょう。
すると、上の状況が「頭の中で描ける」ようになるでしょう。



頭の中でパッと
描けるようになるの?



そうなると、問題を
解くのが早くなりそうだね!
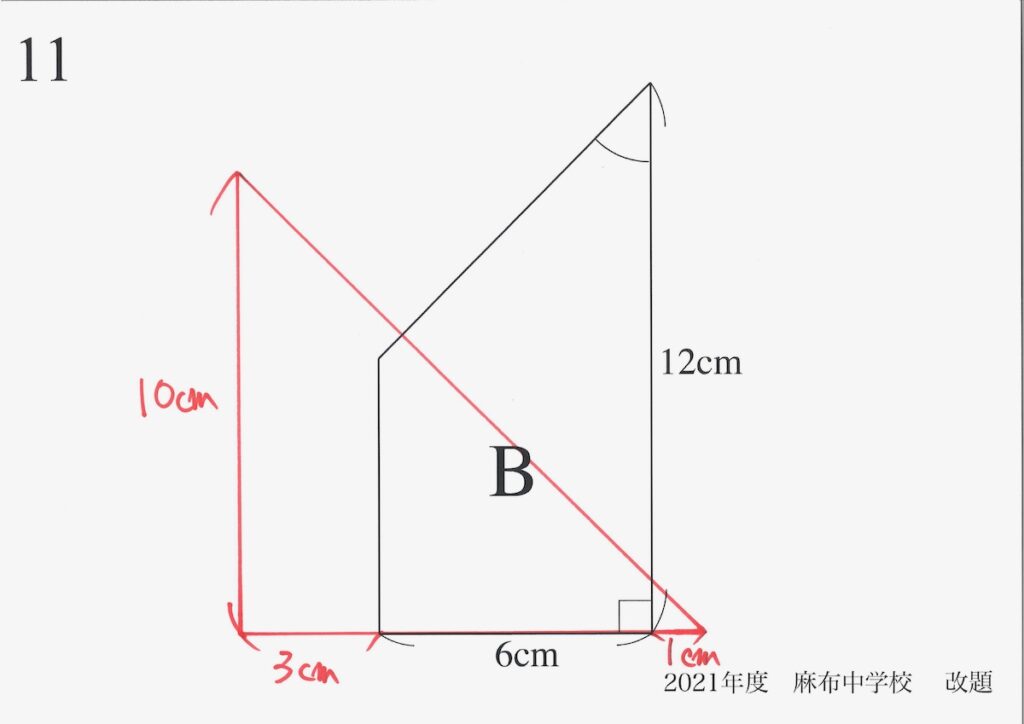

状況をしっかり理解すれば、上記のように「重なる部分」がしっかり分かります。
前回「向かい合った図形が重なり合うまでの時間」は、相対的速さを考えなくても出来ます。
今回の「向かい合った図形がどのように重なるか」は、「両方動く」となかなか難しいです。
「相対的速さ」は自動車や電車の動きをイメージして、ぜひ出来るようになりましょう。
・片方の図形に対する動き・速さ
・矢印で考えて「速さを足す」「速さを引く」で考える
・自動車や電車の動きをイメージ
「直角・同じ長さ」など図形の特徴を把握
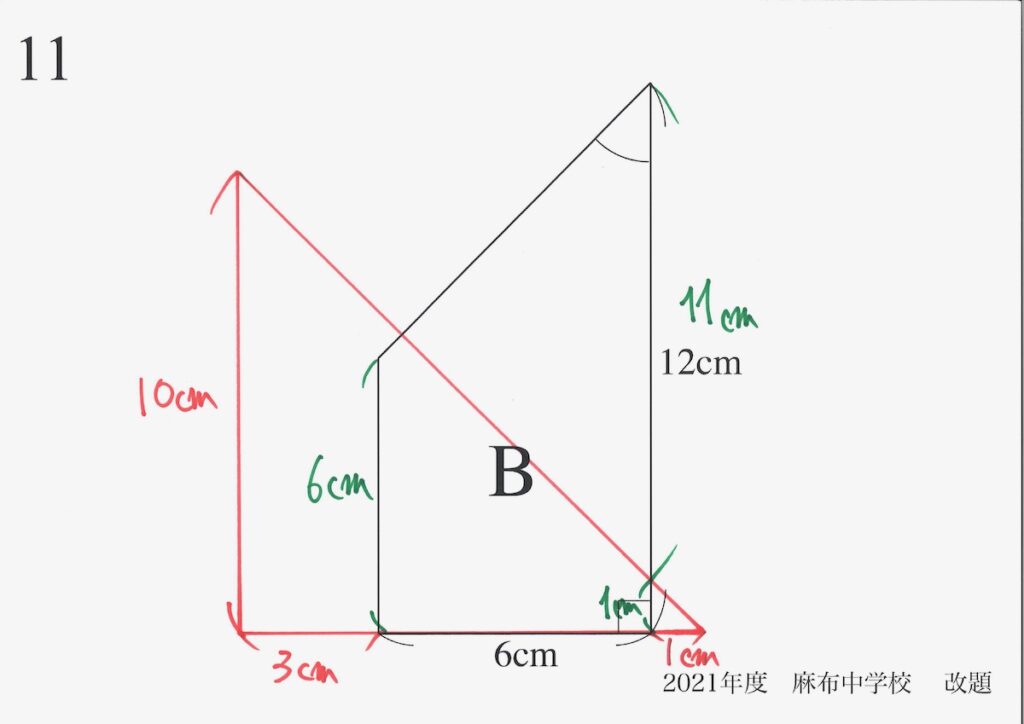

ここまで、しっかり描けることが大事です。
この図形を間違えてしまったら、面積も間違えてしまいます。
「求める面積」を焦って考える前に、「図形」をしっかり理解しましょう。
ここで、元の図形の特徴を考えましょう。



直角二等辺三角形と
台形だね!
右側の台形は「直角二等辺三角形を含む台形」なので特徴的な図形です。
これらの図形が重なると、様々なところに「直角二等辺三角形」が出てきます。
・元の図形の特徴を把握
・元の図形の中にある「正方形・正三角形・直角二等辺三角形」など特徴的図形を発見
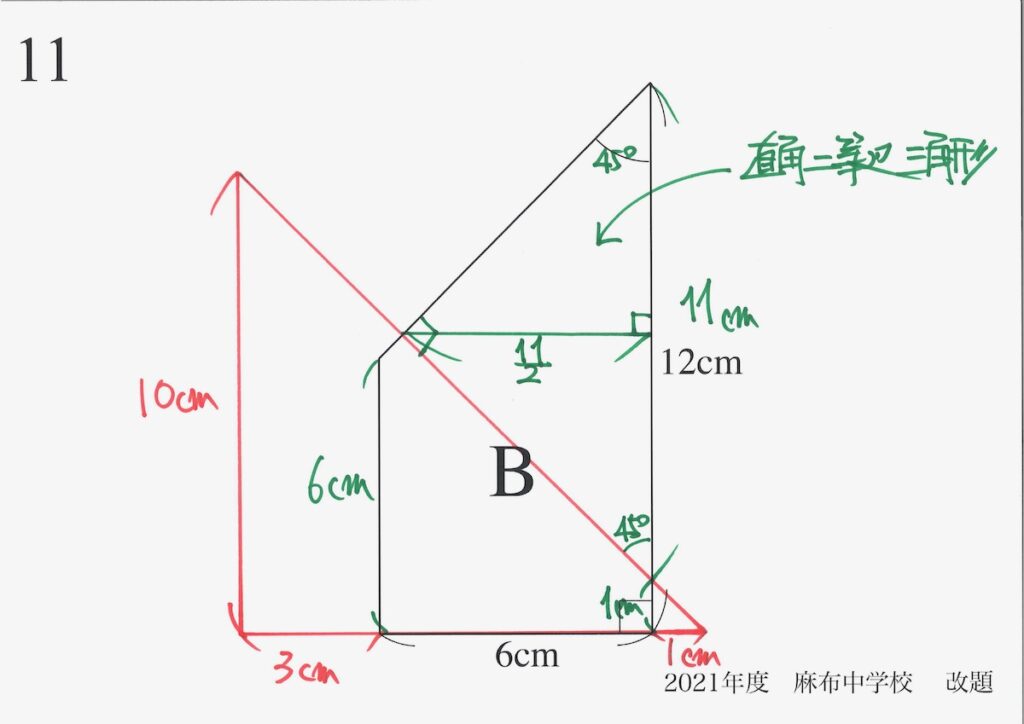

右上の「重なっていない部分」に、直角二等辺三角形が出てきました。
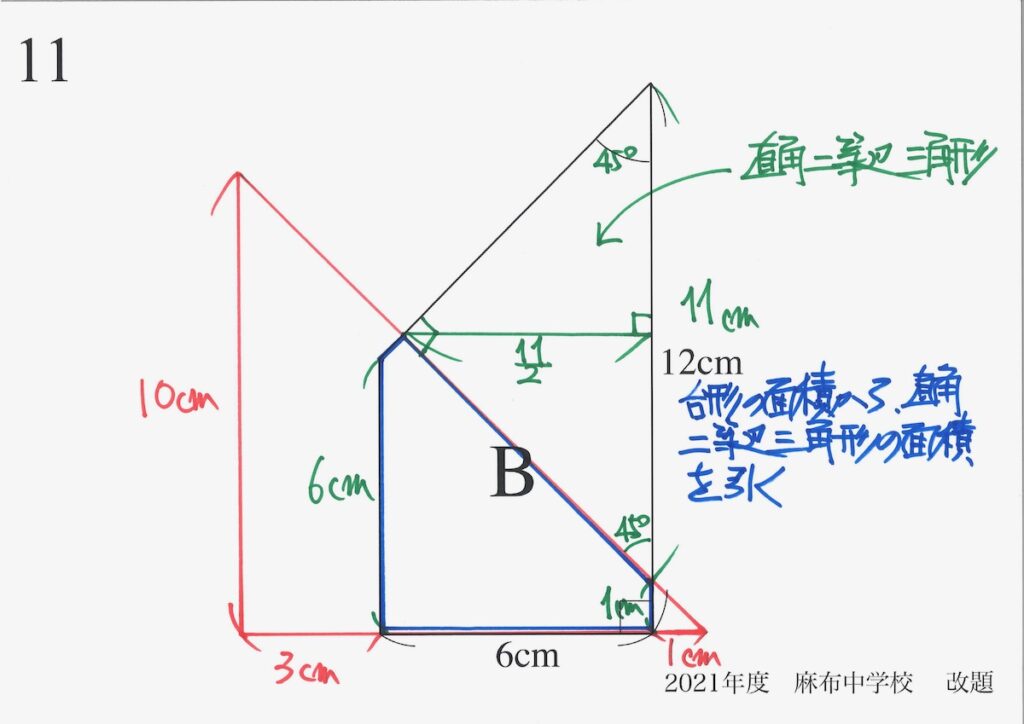

面積は「台形から直角二等辺三角形を引く」で求めましょう。
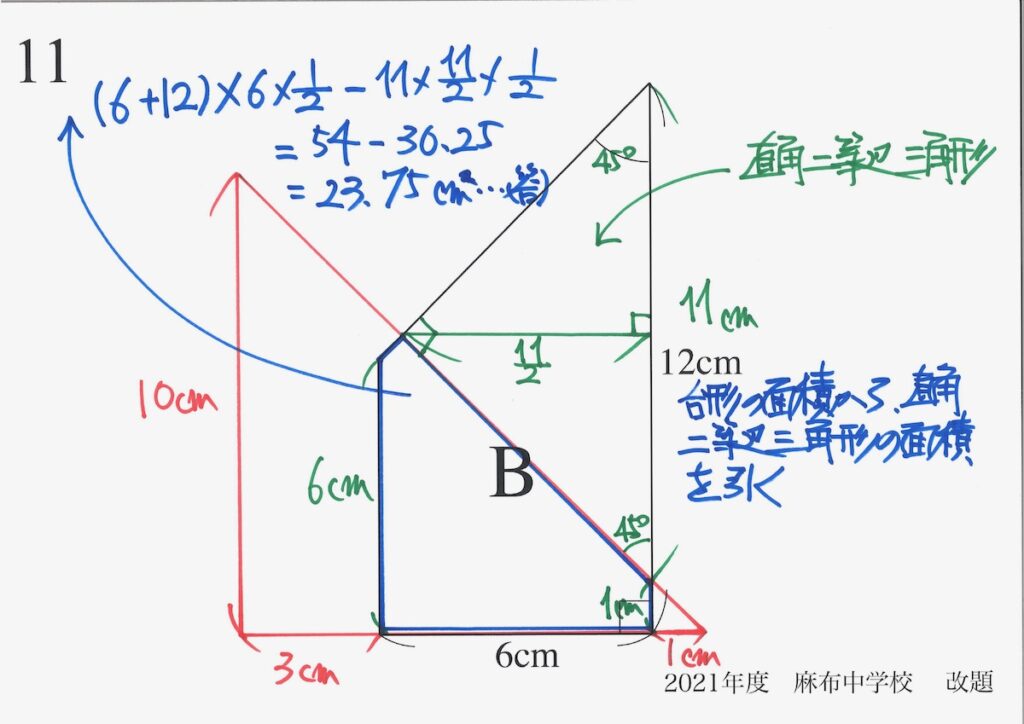

大事な、数字を押さえて計算して、面積が求まりました。
重なる部分の面積=23.75cm2
「重なった部分を分割する」考え方でも良いでしょう。
一つの方法だけでなく、他の方法で「自分で考えてみる」と図形問題の理解が上がります。
次回から、続いて(3)~(5)の問題へ進んでゆきます。
次回は下記リンクです。



