前回は「移動する図形と面積〜「鉄則」「公式」よりも理解する姿勢・公式を自分でつくる姿勢・応用力を育てて学力アップ・問題11〜」の話でした。
問題11（再掲載）
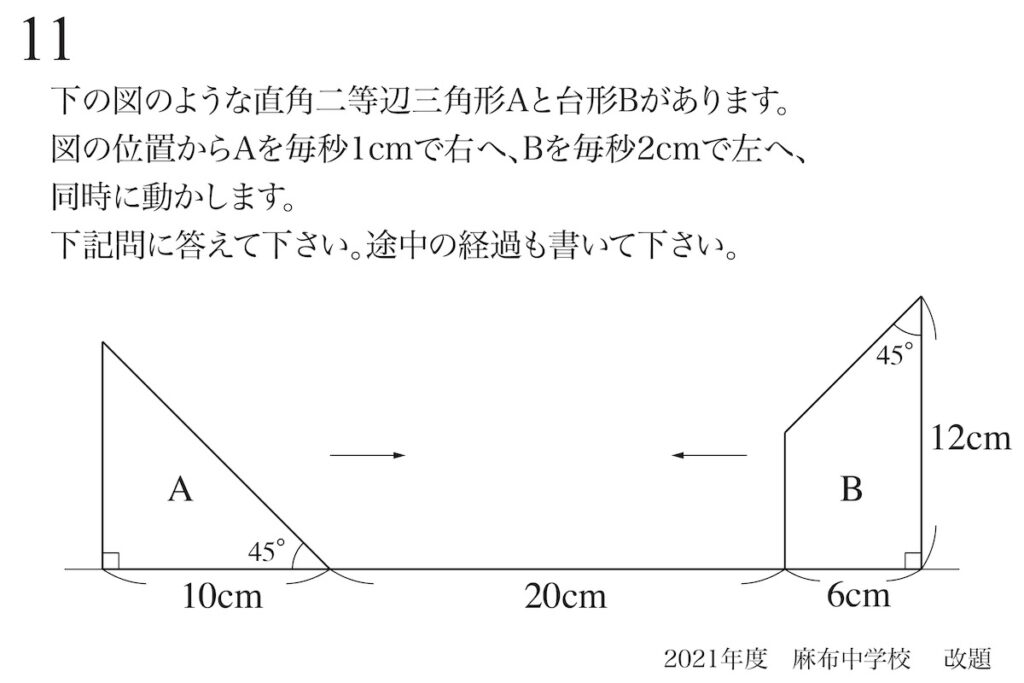
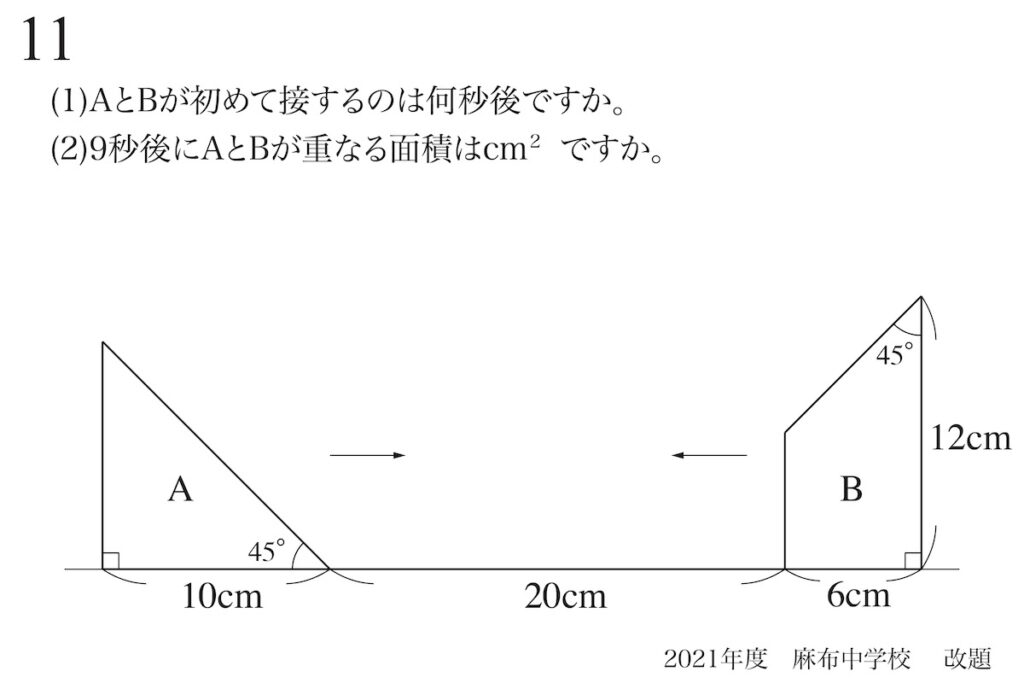
向かい合う点の移動：電車のイメージ
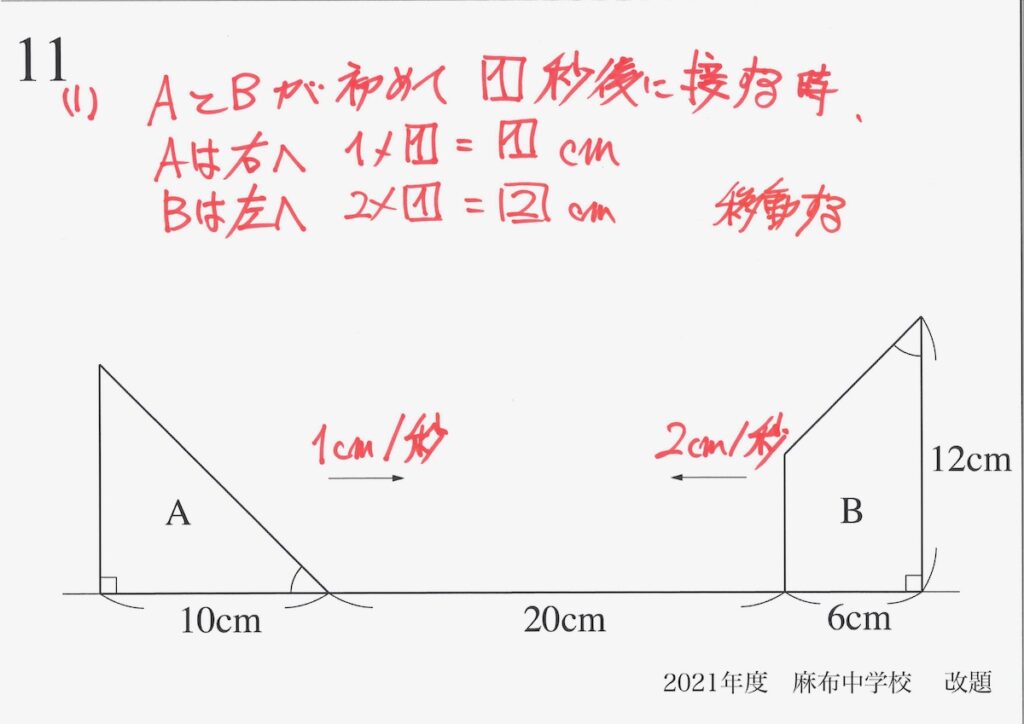
「2つ動くので片方止めて・・・」という考え方があります。
まずはオーソドックスに解いてみましょう。
両方からAとBが向かってきます。
「点が動く」と難しいイメージがあるかもしれませんが、日常生活を考えてみましょう。
電車に乗っていると、「向かい合う反対側から電車が向かってくる」ことがあります。
それと同じように、「動く点」を考えるときは、自分が「動く点」になったイメージを持ちましょう。
そして、「電車の動き」を考えると良いでしょう。
上記の通り、「何秒後に初めて接する」と未知数を設定すると、両方の移動距離が分かります。
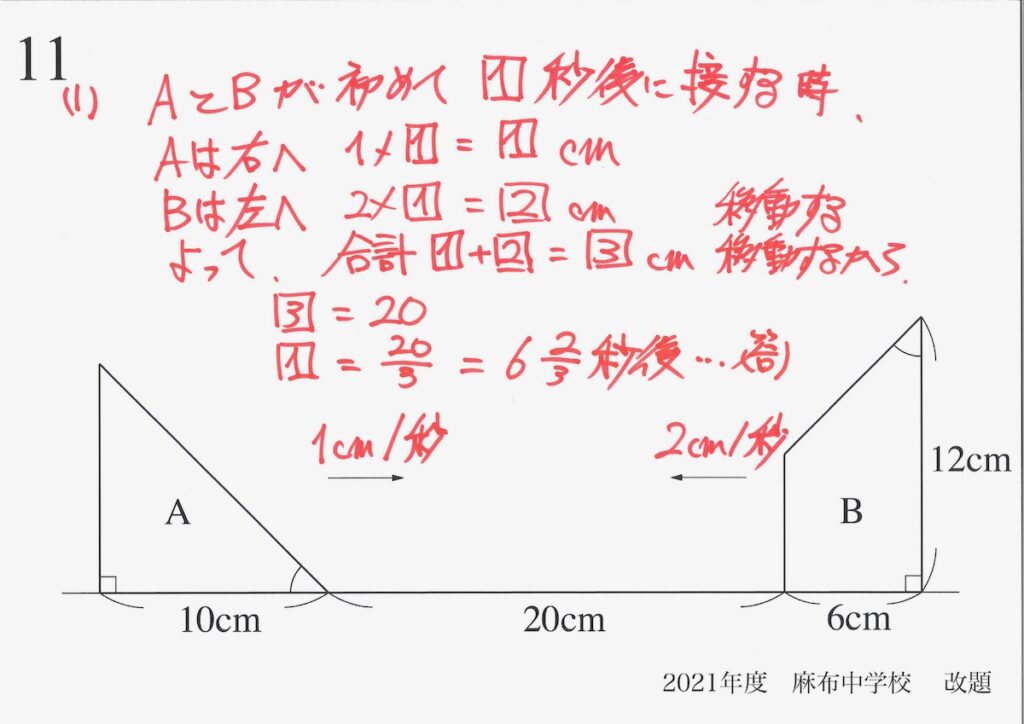
足して計算すれば、初めて接するのが「20/3秒後」と分かります。
男子小学生これでも
いいけど・・・
男子小学生「二つ動くときは、一つ動きを止める」
のがいいんじゃない？
女子小学生そう！
そっちの方が早いね！
動く点の片方を止める：「速さを足す」理由と矢印
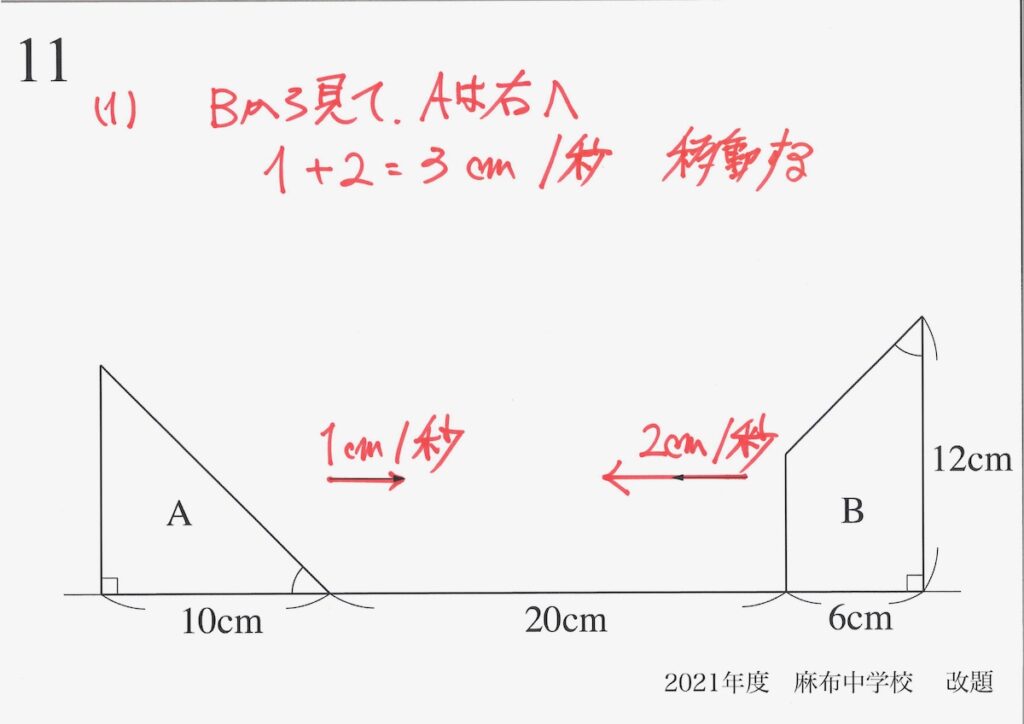
それでは、図形Bからみて、「図形Aがどのように動くか」を考えましょう。
「図形Bを止めて、図形Aを動かす」と同じことです。
BからAを見ると、相対的に「3cm/秒」の早さで向かってくることになります。
「A,B両方動く」状況が「Bを止めて、Aだけが動く」状況になり、簡単になります。
この時、相対的早さは「二つの速さを足す」ですが、しっかり理解できていますか。
男子小学生大丈夫だと
思うけど・・・
女子小学生説明の必要があると、
少し困るかも・・・
先ほどと同じように電車に乗っている時に、追い越したり、向かい合ったりすることを考えます。
今回は、矢印で考えてみましょう。
矢印で図形問題を考えるコツを、上記リンクでご紹介しています。
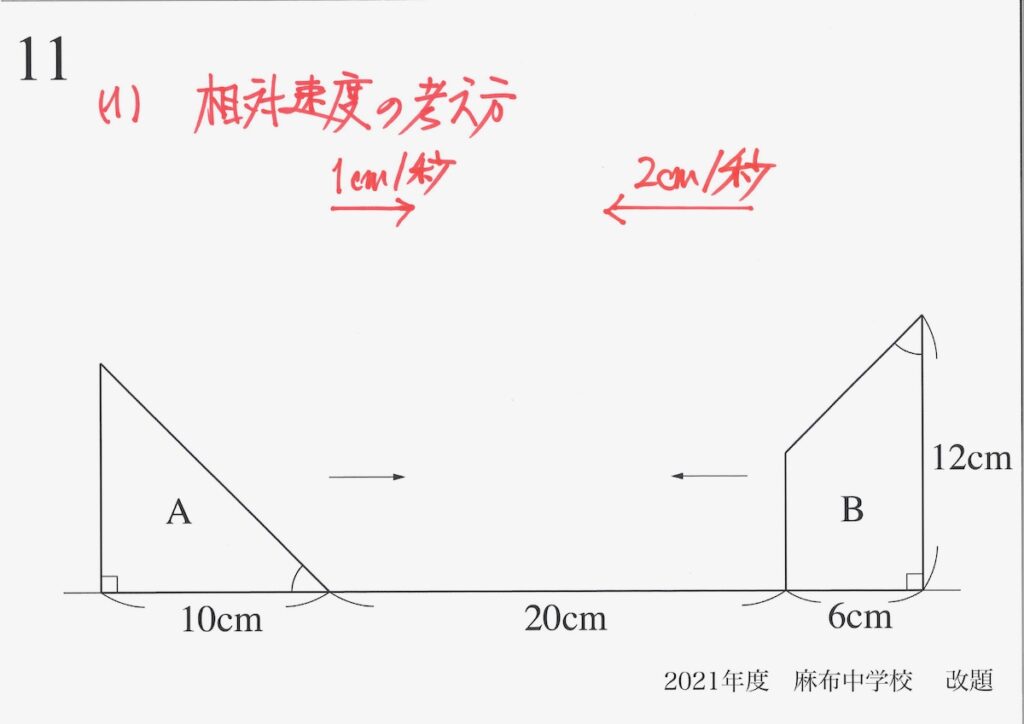
動く速さを「矢印の大きさ（長さ）」で表します。
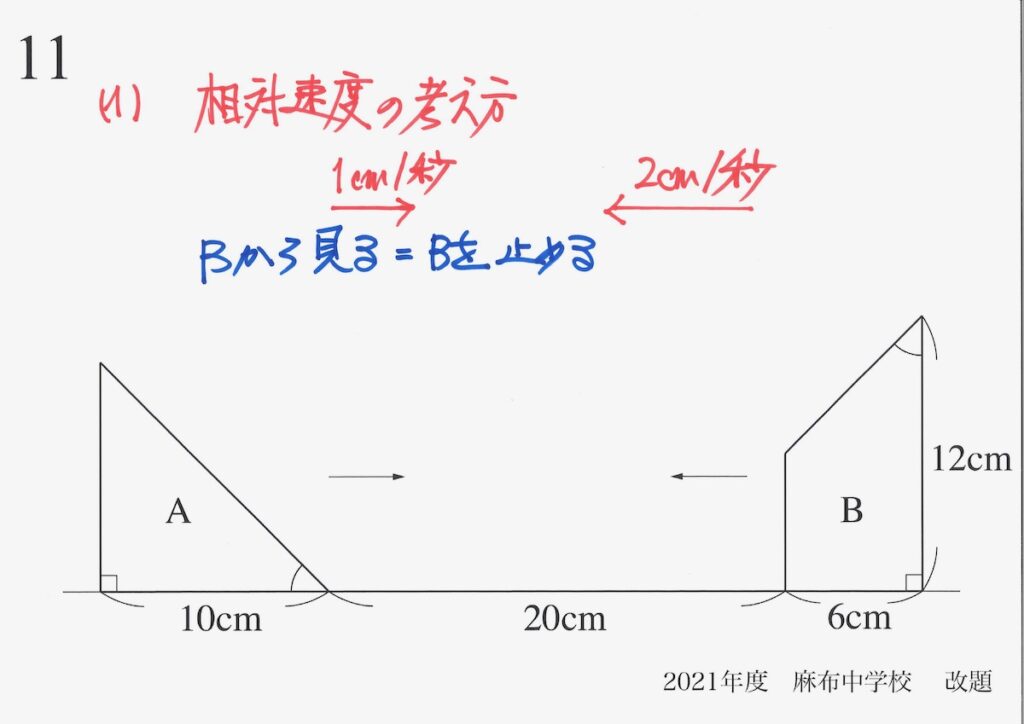
「2cm/秒」は「1cm/秒」の二倍の長さの矢印になります。
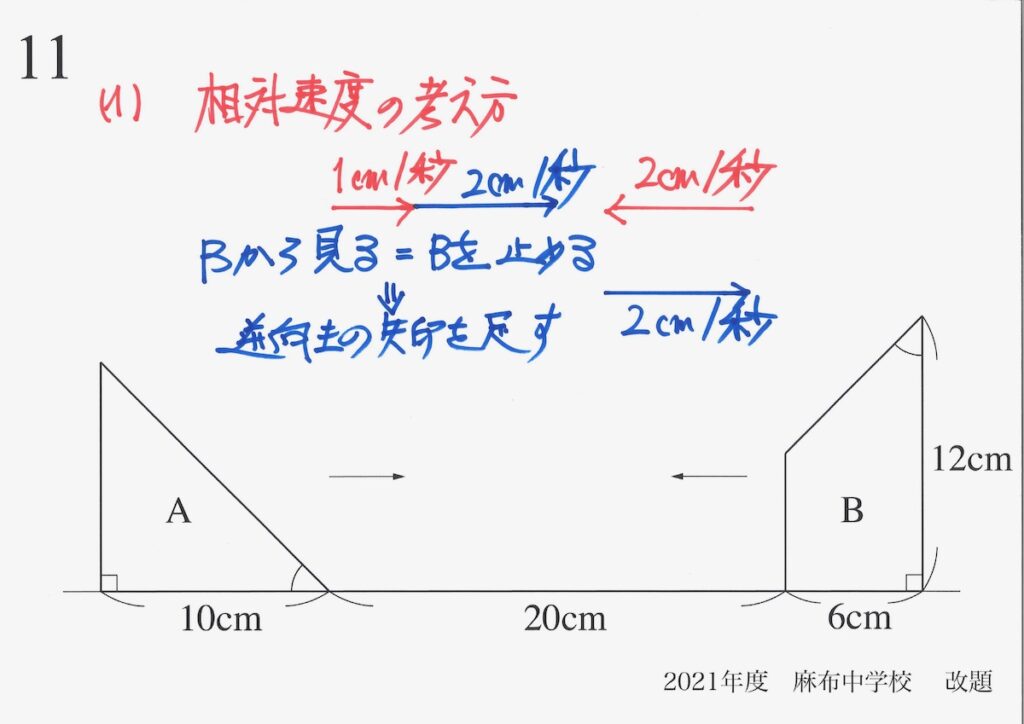
「Bから見る」=「Bを止める」なので、Bを止める方向に矢印を書き加えましょう。
右向きに「2cm/秒」の大きさの矢印を足します。
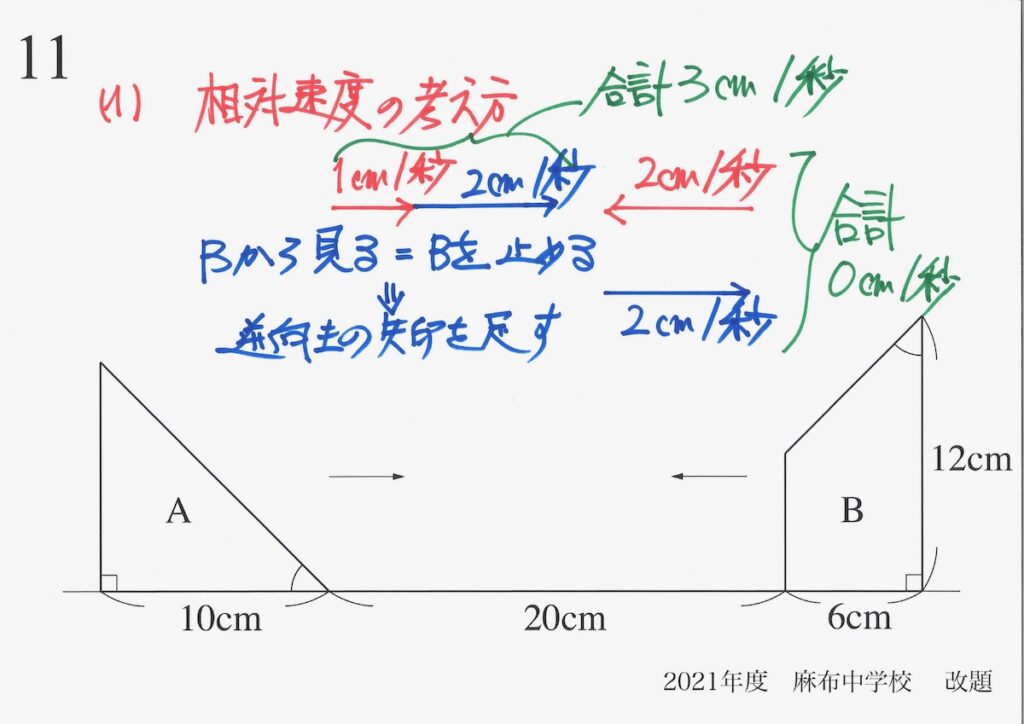
Bの速さの矢印は「逆向きで同じ長さ」なので、合計すると「0cm/秒」となり、止まります。
Aの速さの矢印は「同じ向き」なので、「1+2=3cm/秒」となります。
男子小学生なるほど！
よく分かった！
女子小学生矢印って、
便利だね！
男子小学生図形だけでなく、
「文章題と図形の問題」でも役立つね。
問題が考えやすくなり、上記のように「合計の速さで長さを割る」考え方になります。
もし、上記のような「相対的速さを説明する」問題が出題されたら、電車の絵を描いても良いでしょう。
速さは「同じ時間で移動する距離」と関係するので、「移動距離」で考えても良いでしょう。
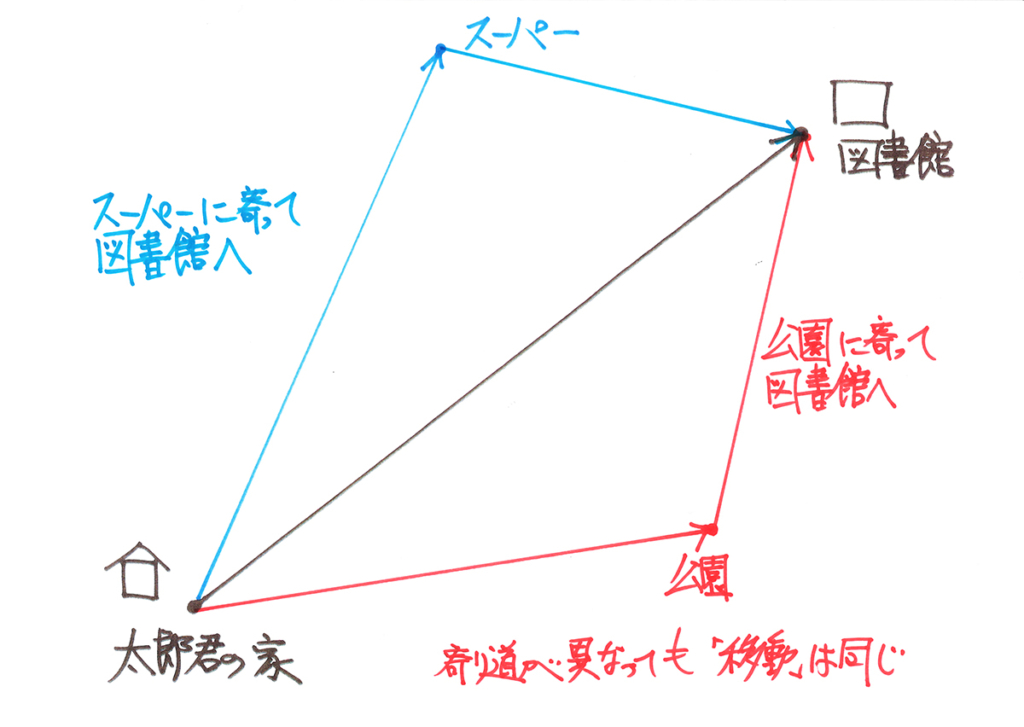
矢印の根本的理解をする話を、上記リンクでご紹介しています。
矢印の話は中学〜高校の数学の内容を含みますが、直感的に理解すると良いでしょう。
男子小学生同じように
「追いかける時は速さを引く」って分かるね！
矢印を考えると、図形問題は色々と考えやすくなります。
ぜひ応用してみましょう。
次回は下記リンクです。
