移動する図形と面積〜「鉄則」「公式」よりも理解する姿勢・公式を自分でつくる姿勢・応用力を育てて学力アップ・問題11〜｜麻布中2021年算数1・過去問・中学受験

前回は「動く点の動き方・解き方と「動く点の気持ち」をイメージ〜「どうなるか」を考える・自分で状況を変えて考える・具体的にイメージ・問題10(5)解法〜」の話でした。

問題11

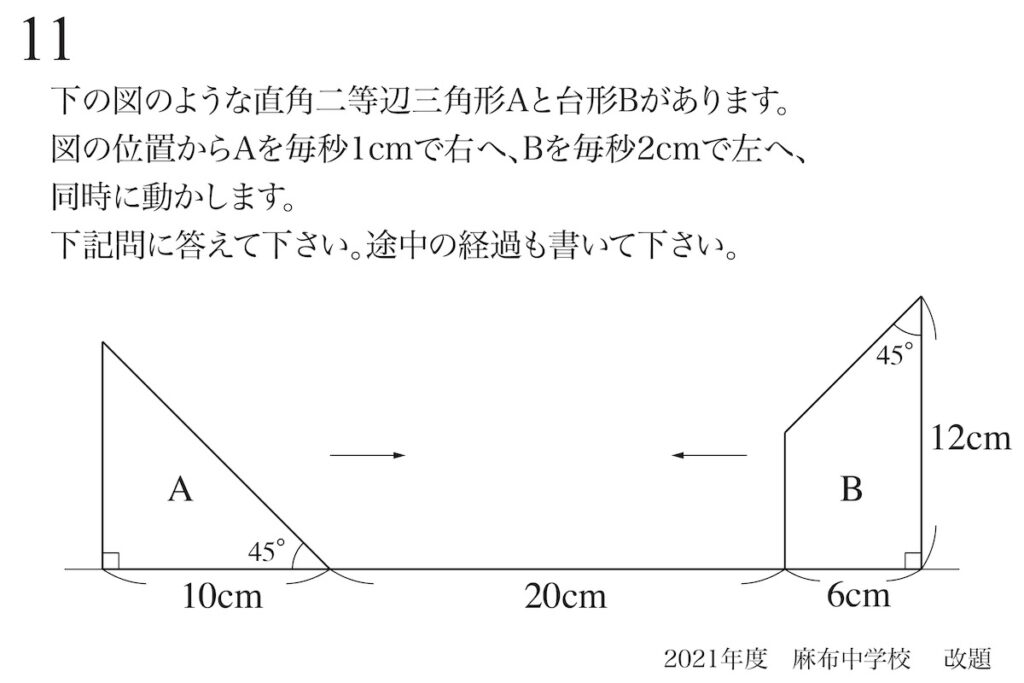
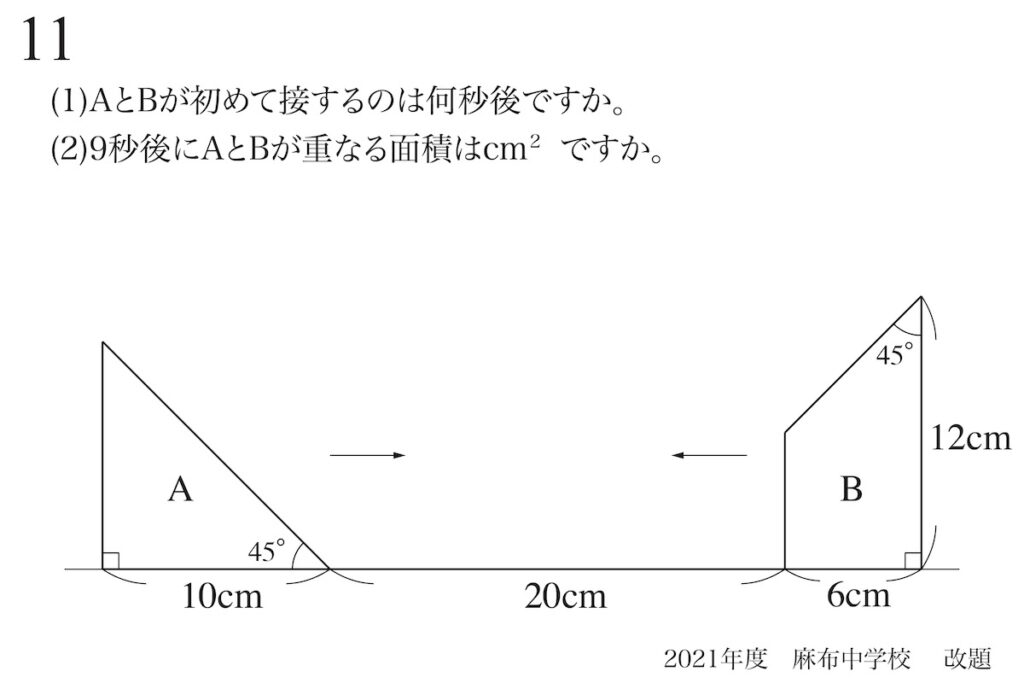
移動する図形と面積：「鉄則」「公式」よりも理解する姿勢

久しぶりの算数実践です。

2021年麻布中学の改題です。

原題は(2)のみで、解いたことがある方も多いと思います。

(1)を追加し、今後いくつかの問題を追加します。

難関校〜最難関校志望の方には、出来て欲しい問題です。

「動く図形は・・・」という「解法の鉄則」みたいな考え方があります。

それを「しっかり理解した上で、考える」ようにしてみましょう。

動く図形に限らず、「鉄則」や「公式」は内容を理解するようにしましょう。

「鉄則」や「公式」を丸暗記していると、「分かりやすい問題」は解けるようになります。

ところが、応用問題などに対しては、丸暗記だけだと、

と「思うように解けない」場合が多くなるでしょう。

「鉄則」や「公式」には、「しっかりした考え方」が背景にあります。

この「しっかりした考え方」をセットにして理解すると算数の学力が、大きく上がるでしょう。

公式を自分でつくる姿勢：応用力を育てて学力アップ

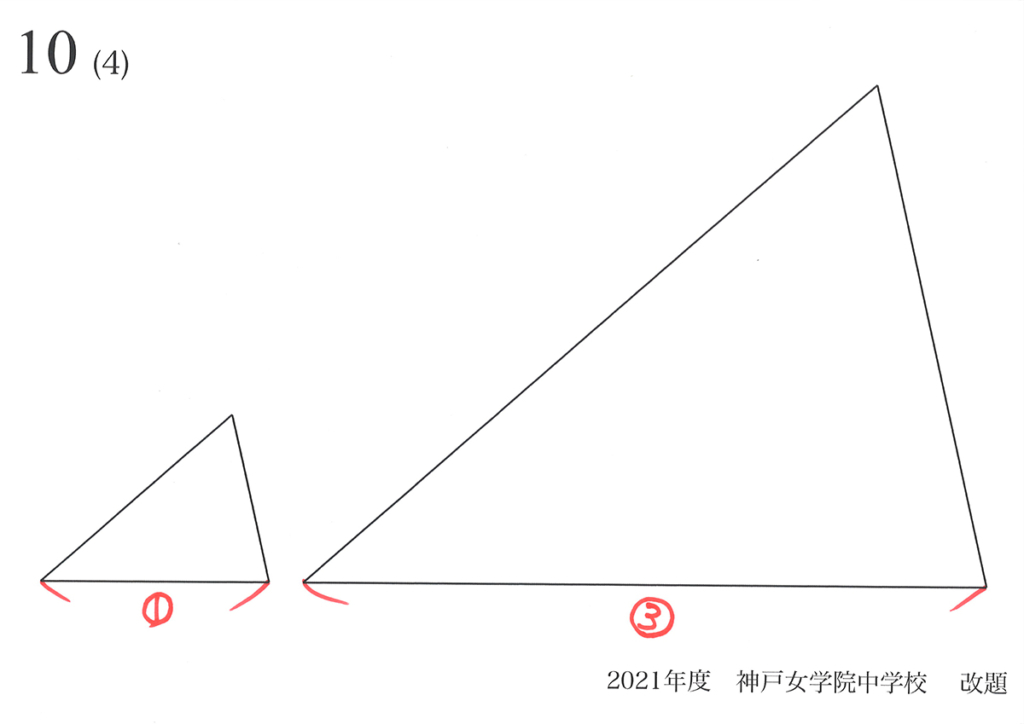
相似形の面積比は「（辺の比）x（辺の比）」です。

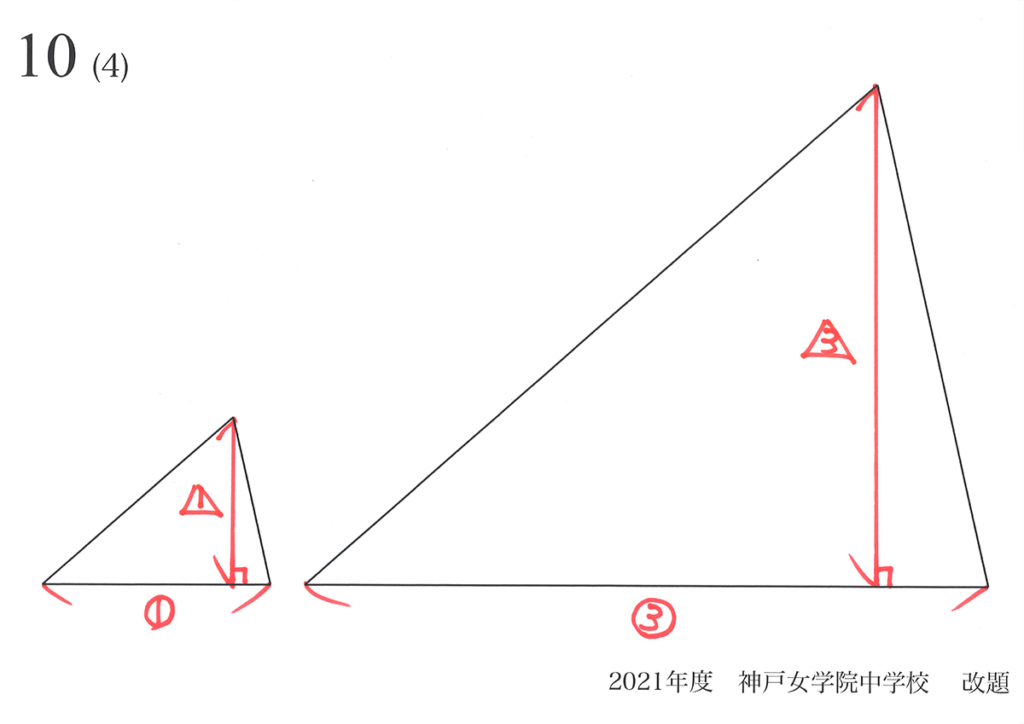
これは大抵の方が知っている公式ですが、説明できる方は少数かもしれません。

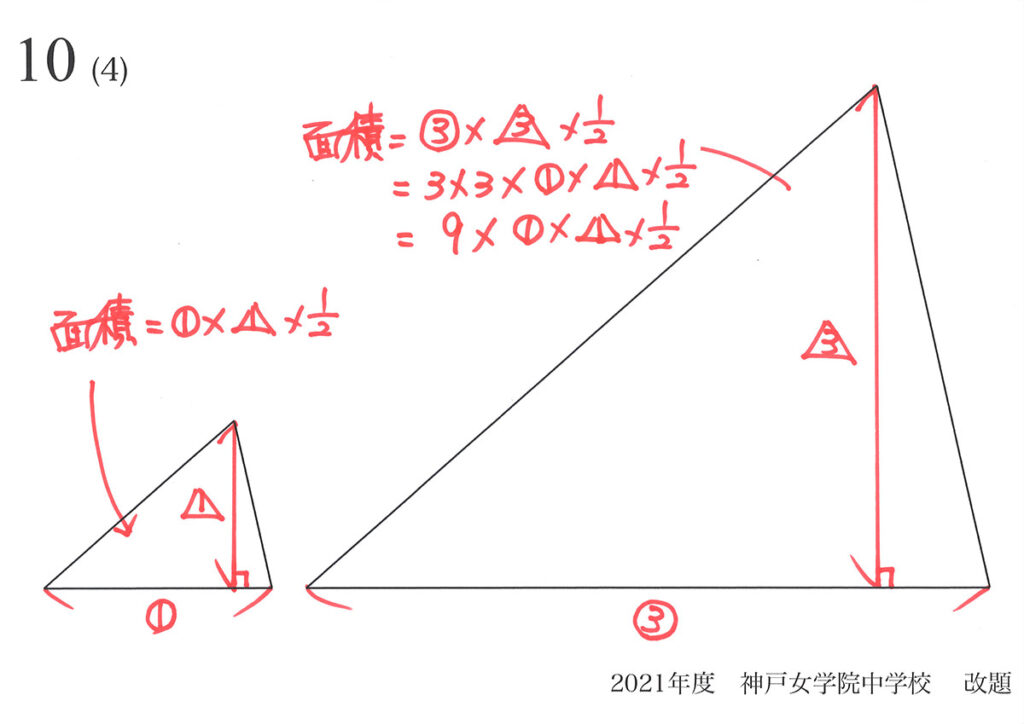
辺の比をしっかり考えれば、面積比が明確に計算できます。

面積比を理解する話を、上記リンクでご紹介しています。

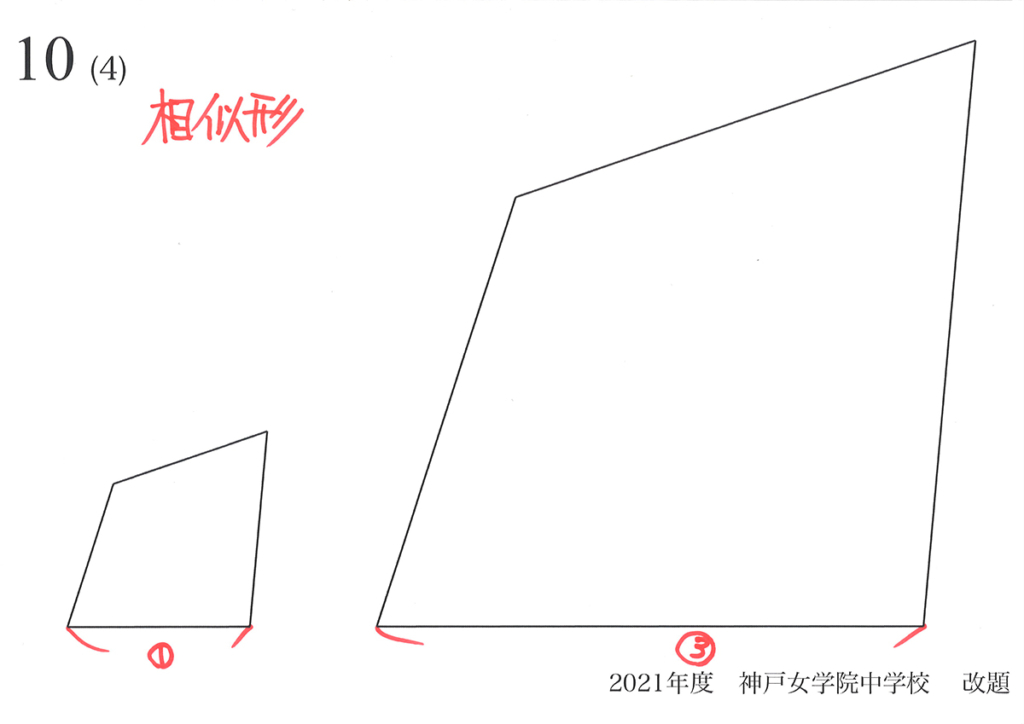
三角形の相似形の「面積比」は比較的簡単ですが、四角形は少し難しいかもしれません。

「平面図形の相似比」は方眼紙に図形を描くイメージを持ちましょう。

すると、「縦・横の辺の比」に応じて「縦・横に引き伸ばされる」イメージができます。

そして、感覚的に四角形でもどんな形でも「相似形の面積比は（辺の比）x（辺の比）」が分かります。

四角形の場合を、感覚ではなくしっかり計算して理解しましょう。

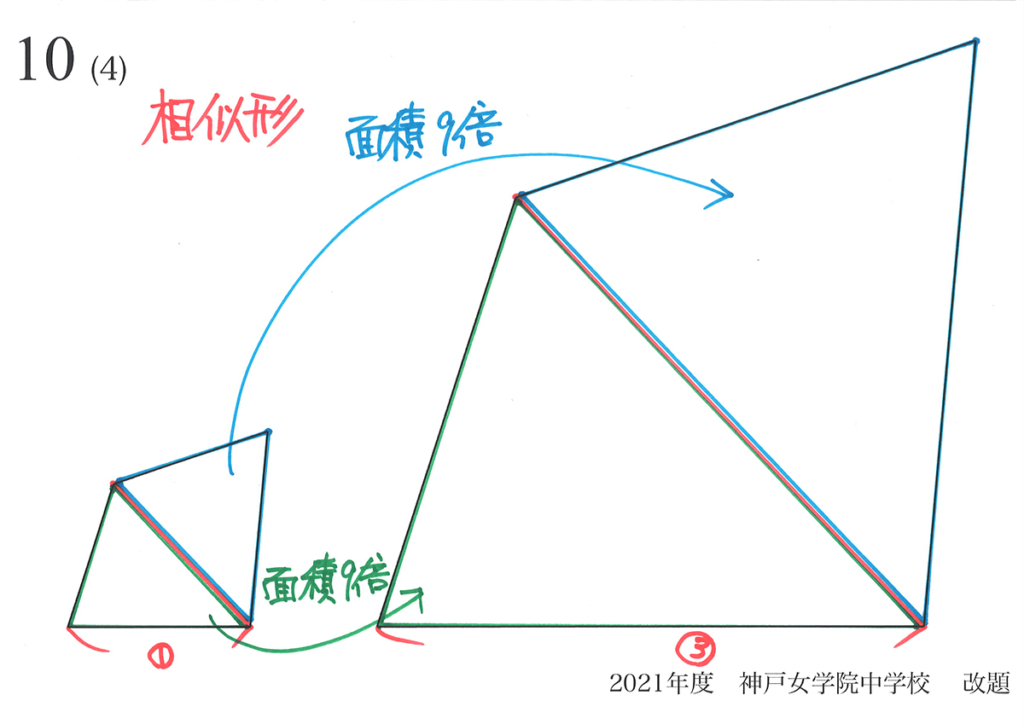
四角形を三角形二つに分割すると、それぞれの三角形の面積比が「（辺の比）x（辺の比）」です。

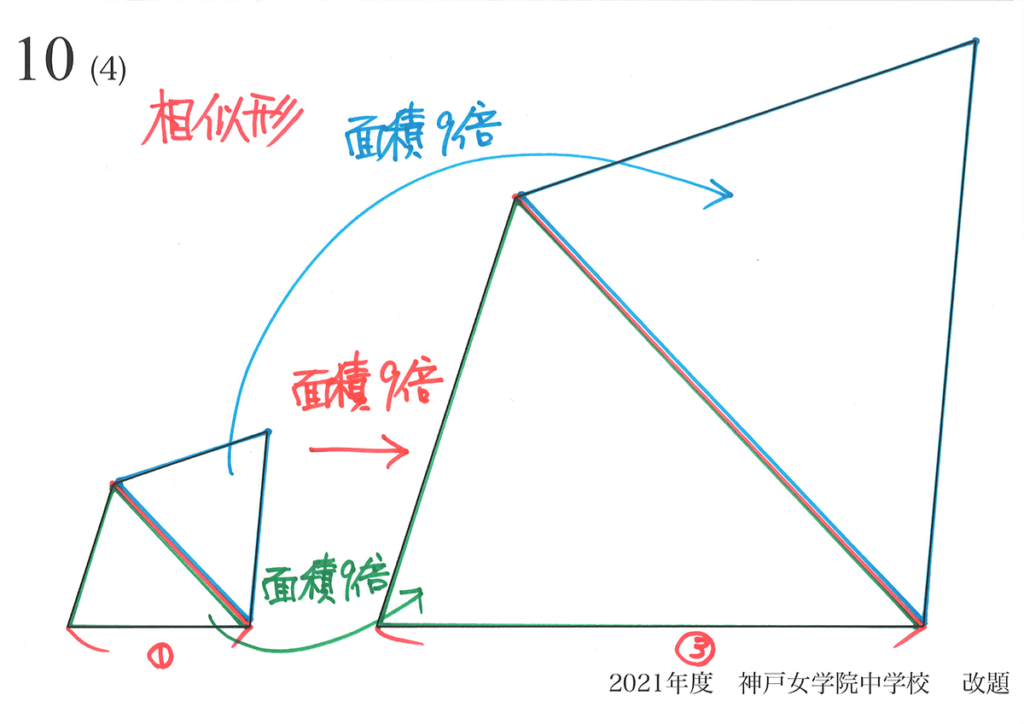
分割した面積が全て共通して「面積比が（辺の比）x（辺の比）」です。

そこで、「分割した図形を元に戻して合計した図形」も「面積比は（辺の比）x（辺の比）」です。

このように考えると、多角形の場合は、すべて「三角形に分割」すればできます。

複雑な曲面でも同様ですが、厳密に計算するのは難しいです。

そこで「分割した図形」と「分割した図形を元に戻して合計した図形」を考えると同じというイメージが大事です。

「公式をしっかり理解する」ことは、応用力も育つ傾向があります。

解法は次回（下記リンク）ご紹介します。