前回は「文章題のおすすめ考え方・解き方〜実験して考える・簡単な場合を考える・状況をしっかり把握・「自分の実験」と答案・考えていることを答案にアピール・「大事な差」に着目・問題3解法A〜」の話でした。
問題3（再掲載）
文章題を「苦手に思わない」考え方：棒グラフや絵を描いてイメージ
男子小学生入れ替えたことで、
なぜ、総重量の違いが起こるのか？
「入れ替えによって何が起こるか」に着目すると、解けました。
その後は、未知数を設定して方程式の要領で解きました。
まず、この方法できちんと解けることが最優先になります。
「10gのおもりより、50gのおもりが9個多い」まで共通します。
こういう問題では、しっかりと状況を把握するために棒グラフを描くようにしましょう。
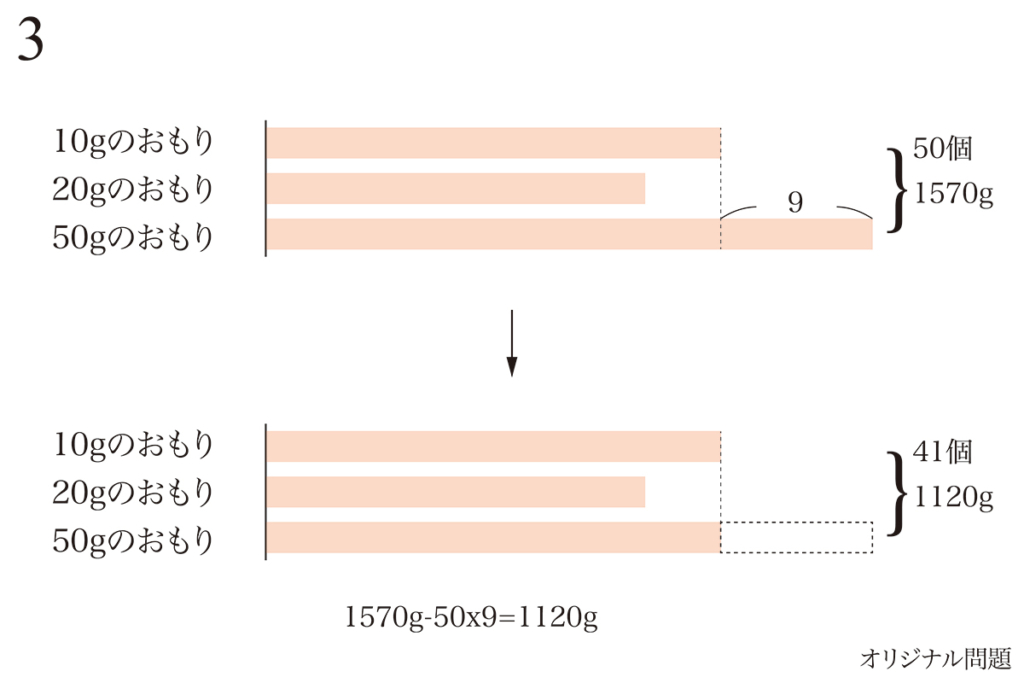
「50gのおもりが9個多い」ため、3つの数量がバラバラで扱いにくいです。
50gのおもり9個を取って、その分の重量を減らしましょう。
女子小学生50gのおもり、9個分
減らすと分かりやすい！
ここで、「10gと50gのおもりのみ」に着目します。
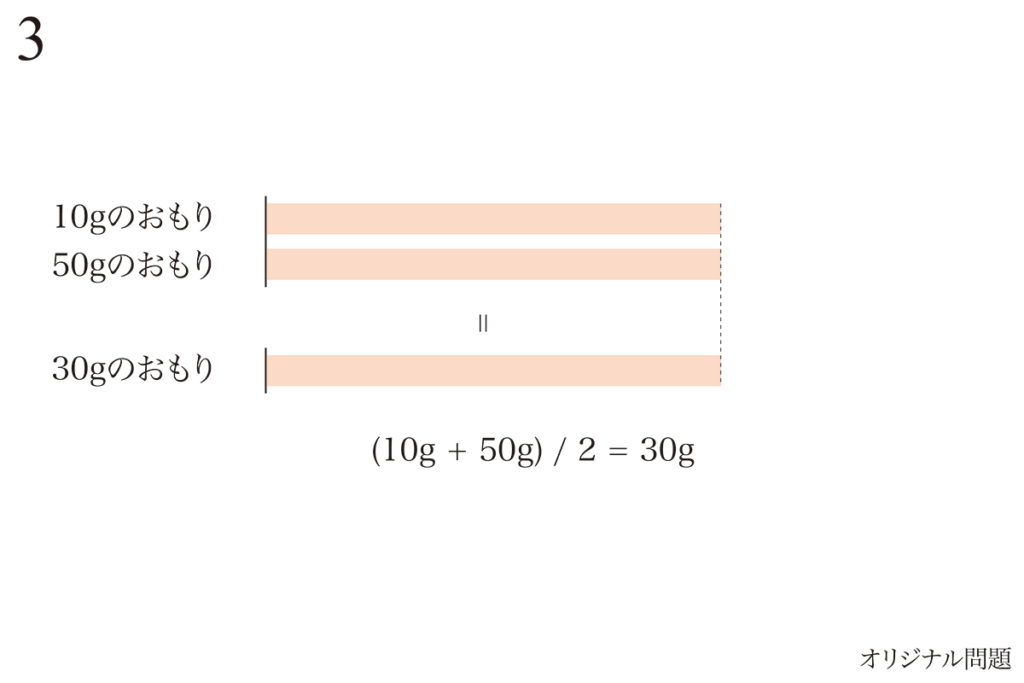
女子小学生あっ、平均を取ると
まとめられるね！
「10gと50gの平均30g」を考えると、二つの棒を一つにまとめられます。
この「まとめる」考え方は大事で「対象が3つ」から「対象が2つ」に絞られます。
棒グラフや絵を描いて「文章題が分かる」
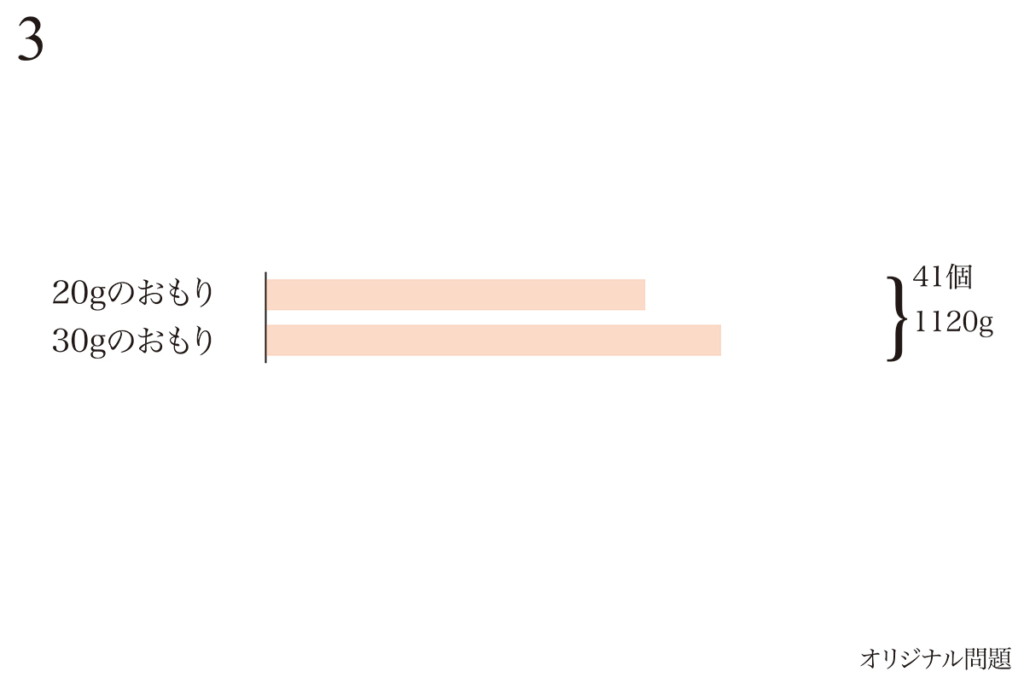
すると、最終的には上の棒グラフになります。
ここからは、つるかめ算の要領で解けますので、略します。
このように、棒グラフや絵を描くと、文章題は非常に見通しが良くなります。
男子小学生うん。
全然分かるようになった！
女子小学生棒グラフって、
文章題では、とても大事！
文章題を読んで分からない時、「文章とにらめっこ」しても、先には進まないことが多いです。
問題を解くときに、簡単な絵を書いて考える話を上記リンクでご紹介しています。
簡単な絵・棒グラフ・グラフなどを描くことを、ぜひやってみましょう。
算数（数学）の学力が、どんどん上がってゆくでしょう。
対象をまとめる発想：「平均」は「ならすこと」
最初の「気づき」の部分は、同一です。
先に書いた通り、途中から未知数を設定して①などと置くことは解法としては考えやすいです。
解法Bの方が「平均」を考えている点で、本質的と言えます。
「平均」とは「ならすこと」です。
小学生らしく、発想が柔軟な感じがします。
未知数設定による方程式による解法は、中学から学ぶ数学である代数学の最も大事なコンセプトです。
それを算数に取り込んで、X,Yという「難しそうな雰囲気」を①などに置き換えて、小学生は考えます。
小学生らしい発想で算数を考える話を、上記リンクでご紹介しています。
方程式的に解くよりも、小学生らしい柔軟性を持って解決した方が、望ましいように感じます。
①などの未知数を設定して粛々と解くよりも、考えに柔軟性があって伸びそうです。
中学校の教育理念にもよりますが、このように「平均を考える」などのコンセプトで解いていると、
採点者おっ、
いいね！
採点者この発想は
とっても良いな・・・
採点者は良い評価を与え、相応の点数を与えるでしょう。
方程式の発想も大事ですが、上記のような「3つを2つにまとめる」という発想も、応用がきく大事な考え方です。
ぜひ身につけて下さい。
次回は下記リンクです。
