前回は「図形・正六角形の解き方〜対称性のある図形の大事なポイント・中心・対称性・対称軸・まず相似形を探す・平行な辺に着目・辺の長さの比と面積比・問題4(1)解法〜」の話でした。
問題4(再掲載)

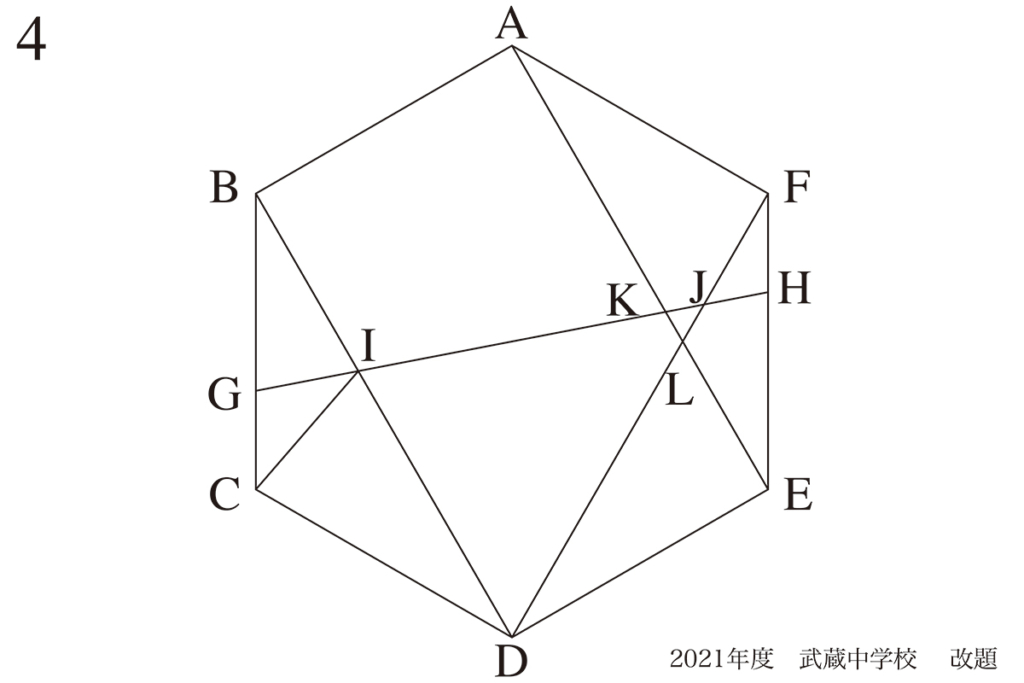
少しずつ面積を求める:分かっていることを図形に描く
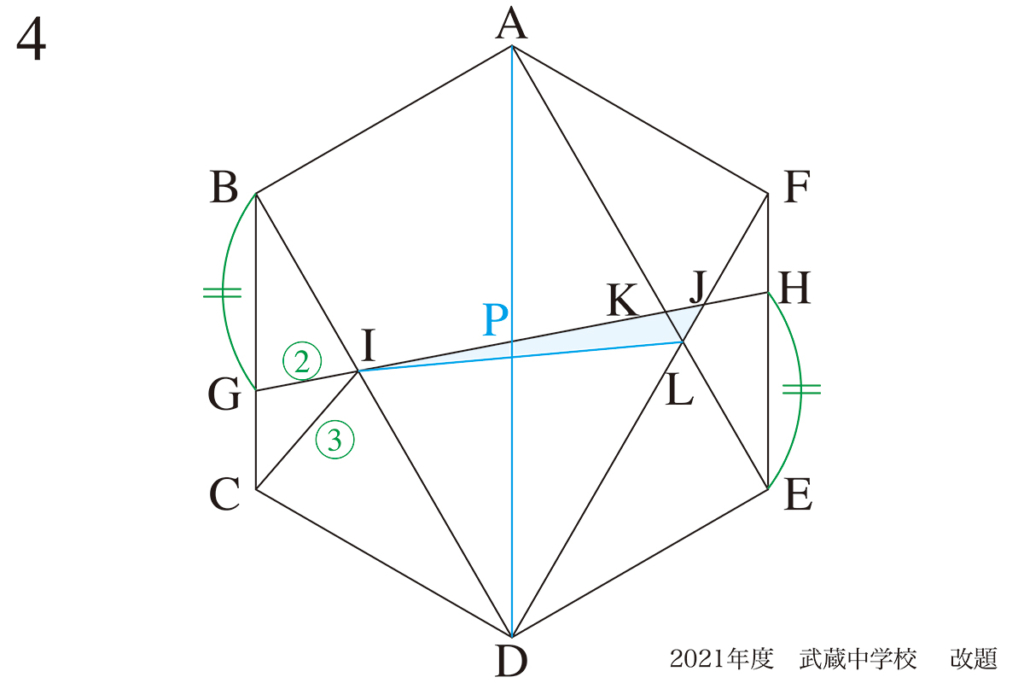
今回は(2)の解法です。
とても小さな△JKLの面積を求める問題です。
こういう時は、
 男子小学生
男子小学生一気に
解こう!
このように「一気に」ではなく、



少しずつ、分かるところから
考えてゆこう!
着実に考える姿勢が大事です。
・一気に考えるのではなく、分かるところから徐々に考えてゆく
・図形に「わかっていること」を描いて整理する
△JKLの面積を求める一段階前の三角形の面積として、下記の△IJLを考えましょう。
(1)でわかった比を元に、他の辺の比を求めてゆきます。
BC,AD,FEが平行なので、相似三角形はたくさん見えてきます。
△APKと△HEKが相似→PK : KH =3 : 2
△PJDと△HJFが相似→PJ : JH =3 : 1
並んだ点の長さの比を整理:対称性・対角線

並んでいる点P,K,J,Hは、PK, KJ, JHの三つの辺があり、関係する比が求まりました。
比が合計3+2=5、下の比は合計3+1=4 なので、5と4の最小公倍数20を考えます。



最小公倍数を
考えるんだね!
比を按分して、辺の比を求めましょう。
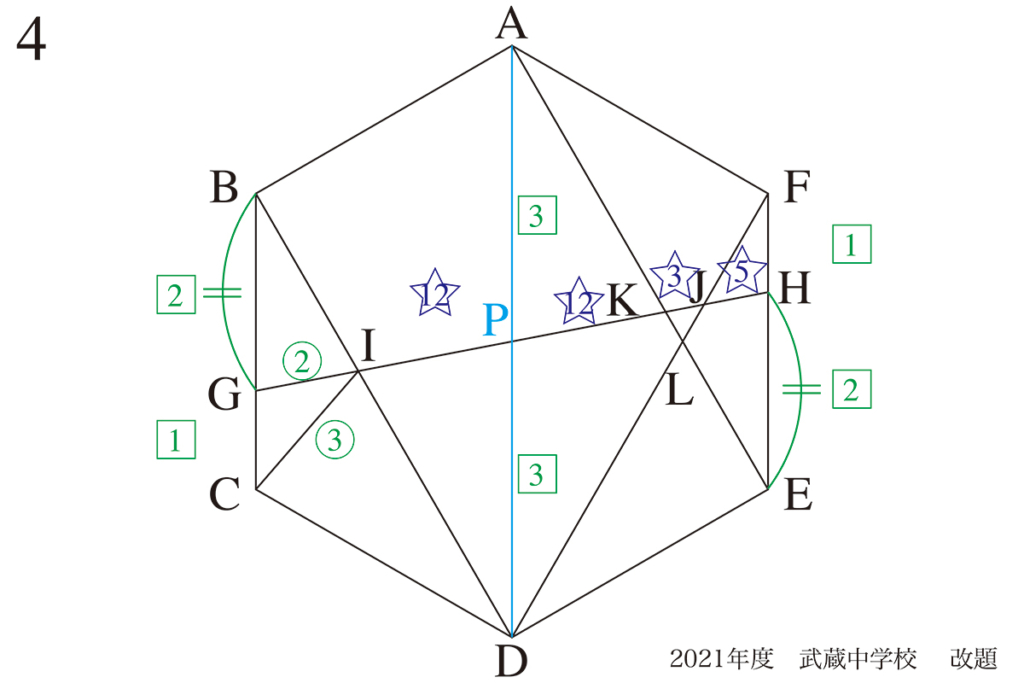
PK : KH =3 : 2 → 4をかけて → PK : KH =12 : 8(比の合計は20)
PJ : JH =3 : 1 → 5をかけて → PJ : JH =15 : 5 (比の合計は20)
PK : KJ : JH = 12 : 3 : 5 と求まり、IP=PKであることが分かります。
連比と最小公倍数:相似形の面積比

同様に△PJDと△HJFが相似→DJ : JF = 3 : 1
△ALDと△ELFは相似→DL : LF =2 : 1
上の比が合計3+1=4、下の比は合計2+1=3 です。
そこで、4と3の最小公倍数12を考えて比を按分して、辺の比を求めましょう。
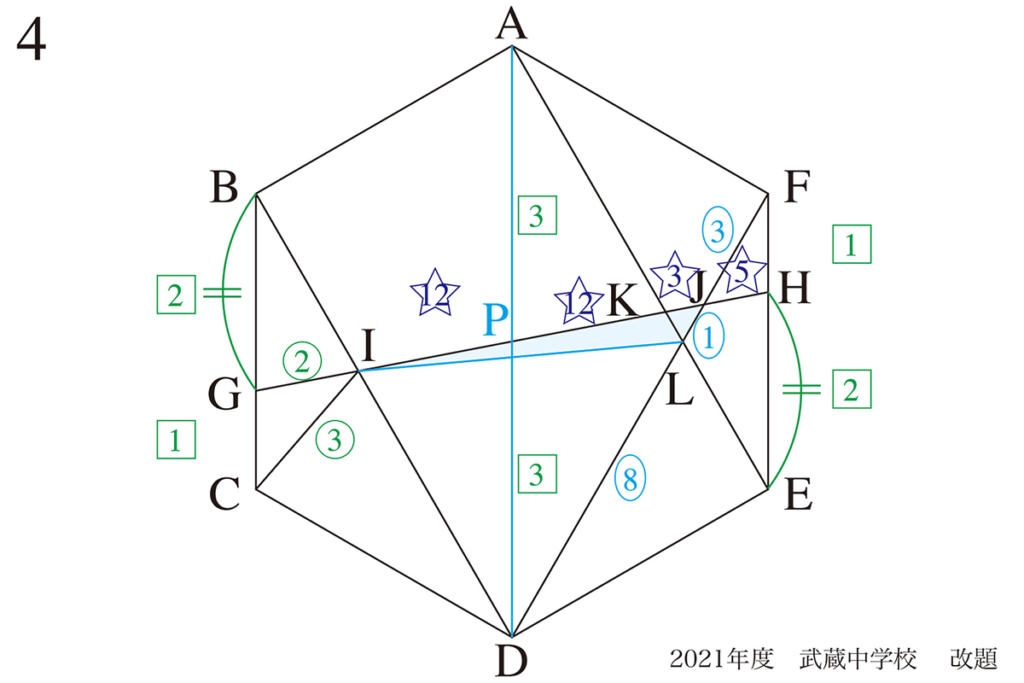
DJ : JF = 3 : 1 →3をかけて→DJ : JF = 9 : 3(比の合計は12)
DL : LF =2 : 1→4をかけて→DL : LF =8 : 4(比の合計は12)
DL : LJ : JF=8 : 1 : 3 と求められます。



辺の比が
少しずつ分かるね!
これで、(1)で求めた△DIJの面積を元に、下記のように求められます。
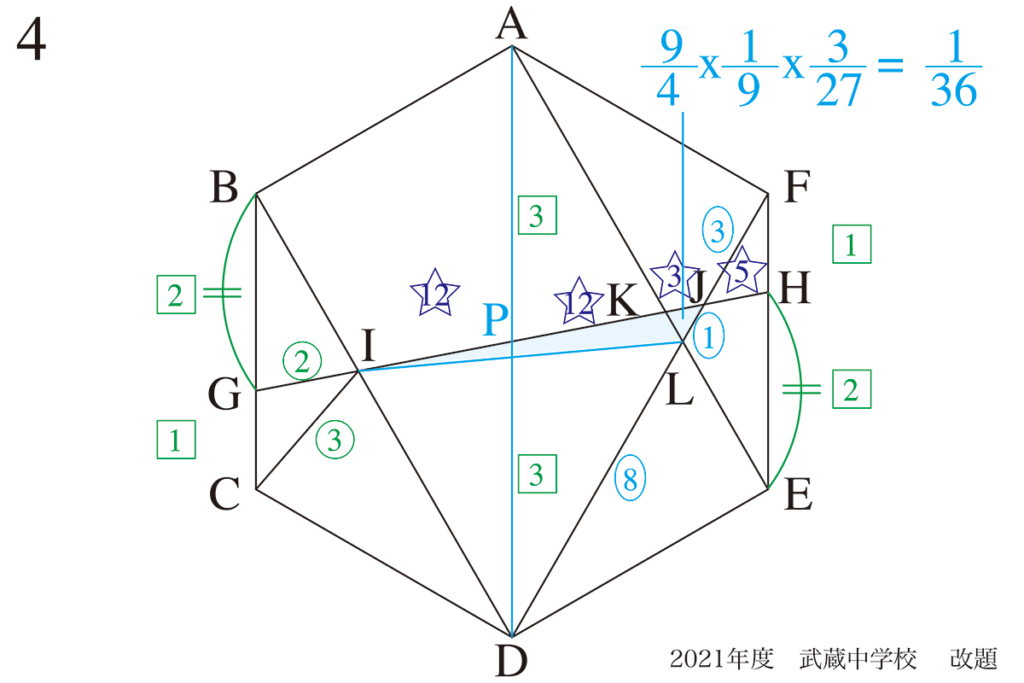

答えは、1/36です。
1/36
この解法が最もオーソドックスです。
あることに気づくと、少し計算が省略できます。
また、その「あること」は図形に関して、非常に大事なことです。
ヒントは「平行」で、少し考えてみてください。
次回は下記リンクです。


