前回は「グラフの読み取りのポイント・コツ〜図形と現象の対称性・グラフが「分かる」姿勢・大雑把に考える・「大体分かる」ことも大事に・図形や現象の変化をイメージ・問題10(5)解法〜」の話でした。
問題10(5)再掲載
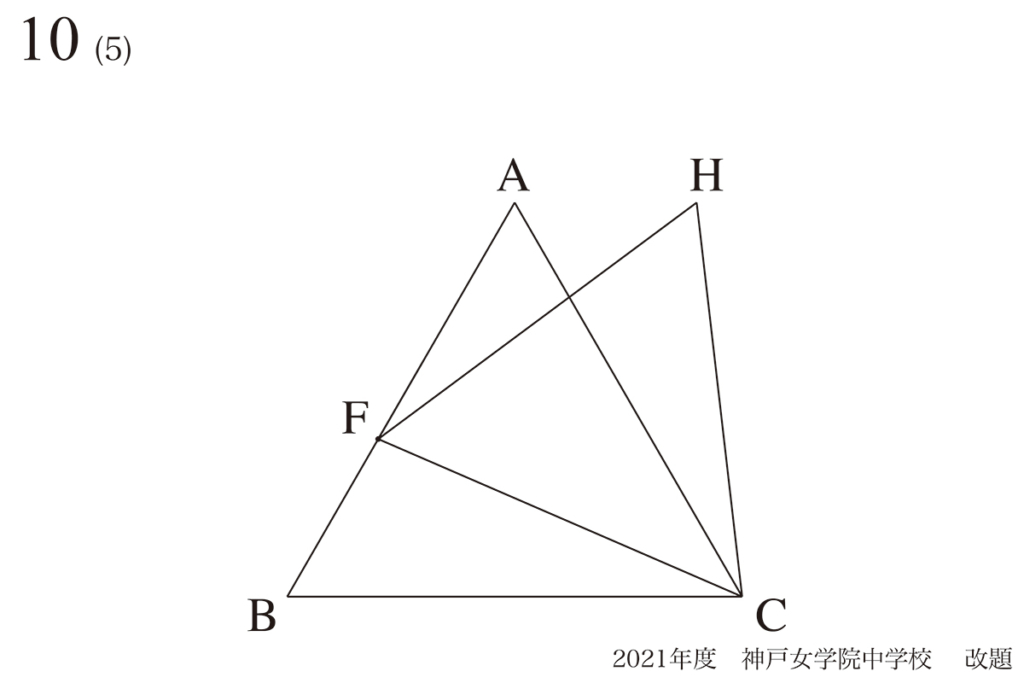
「動く点の気持ち」をイメージ：「どうなるか」を考える
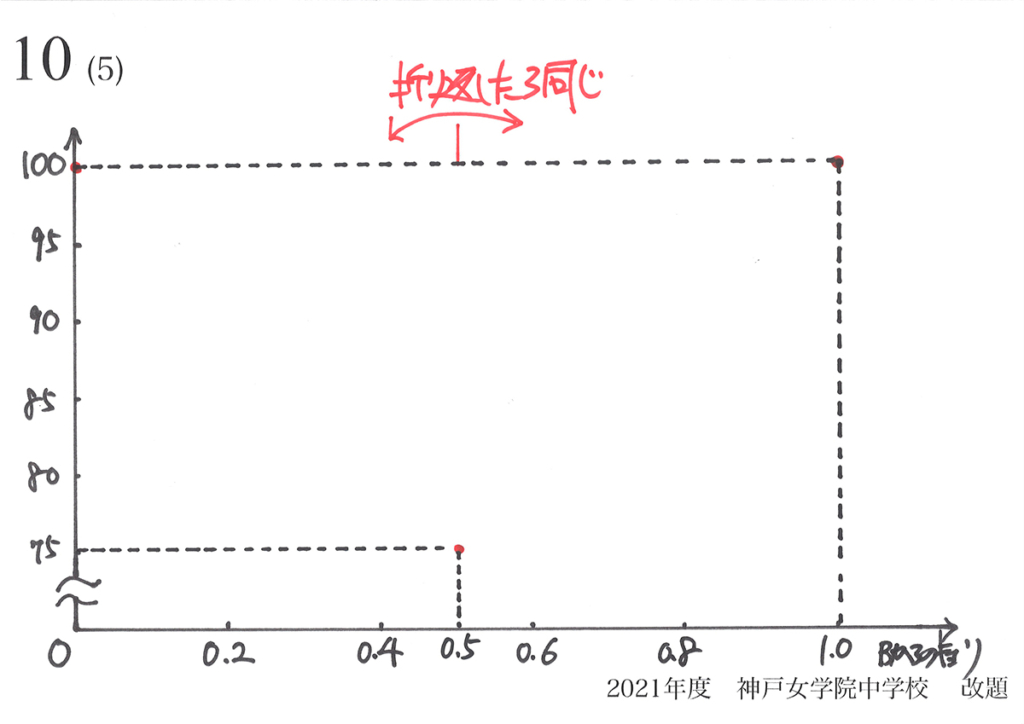
正三角形FCHの面積を考えるとき、「最大・最小しか分からない」時を考えました。
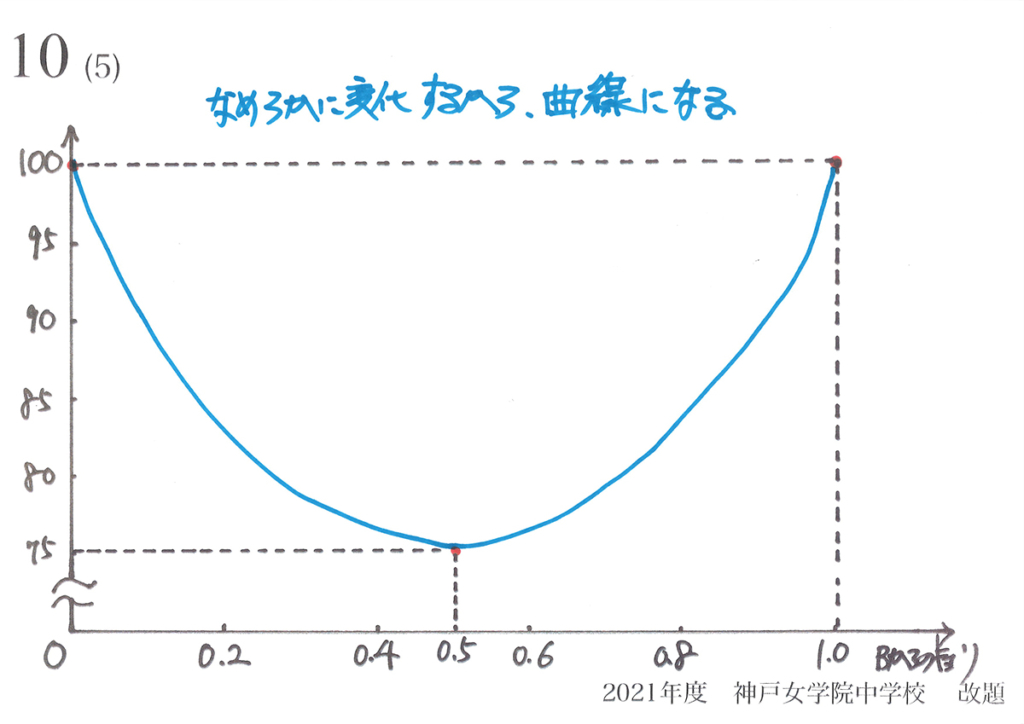
ポイントは「なめらかにつながる」でした。
正三角形の面積は「正三角形の（一辺の長さ）x（一辺の長さ）」に比例します。
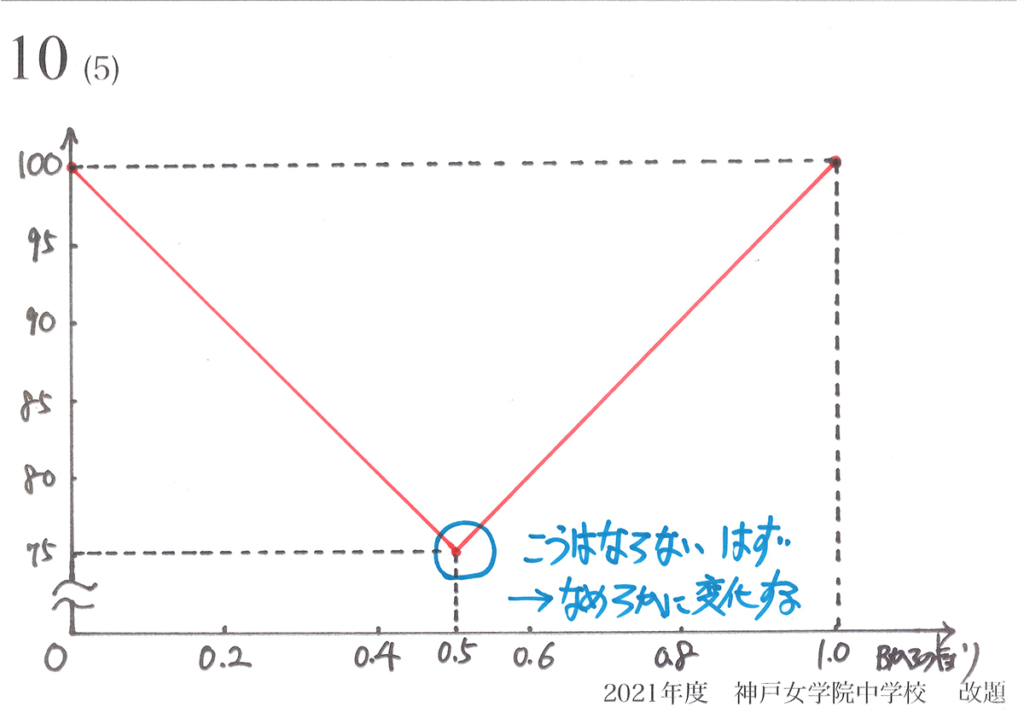
そのため、上のグラフのように「どこかが尖ったグラフ」になるのは、不自然なのです。
そこで、「徐々に変化して、なめらかにグラフの曲線が出来る」イメージを持ちましょう。
男子小学生ちょっと、いまいち
良く分からないよ。
女子小学生分かるような、
分からないような、不思議な気持ち・・・
ここは「なんとなく分かる」でも良いでしょう。
少し状況を、変えて考えてみましょう。
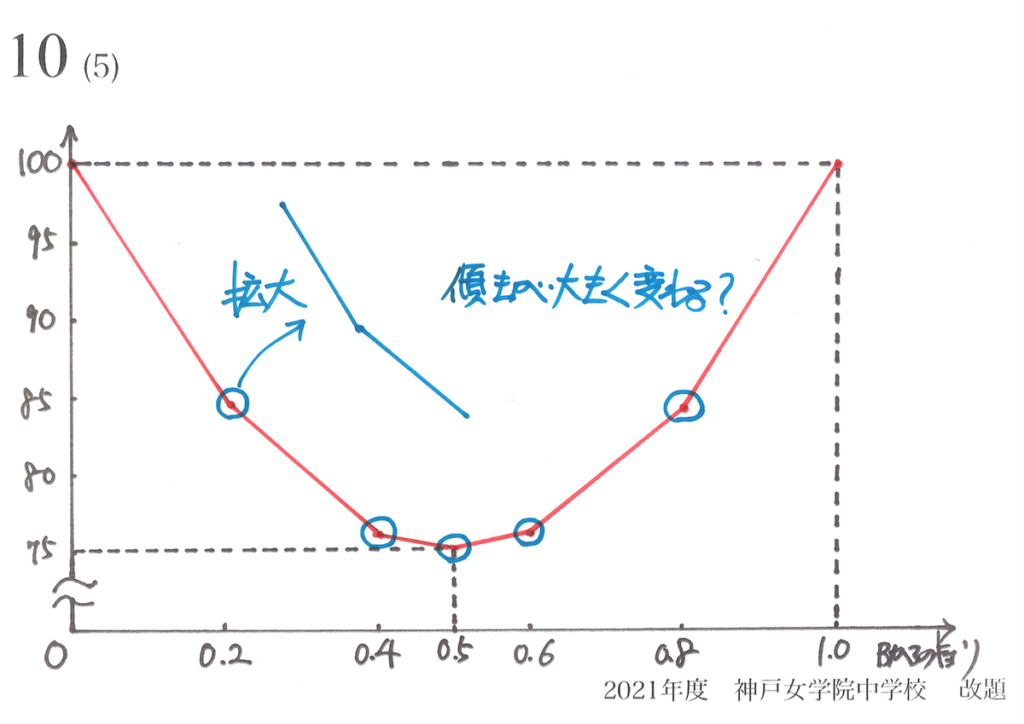
今回は「辺ABを五等分する点」を考えました。
それでは、「辺ABを十等分する点」を考えたらどうなるでしょうか。
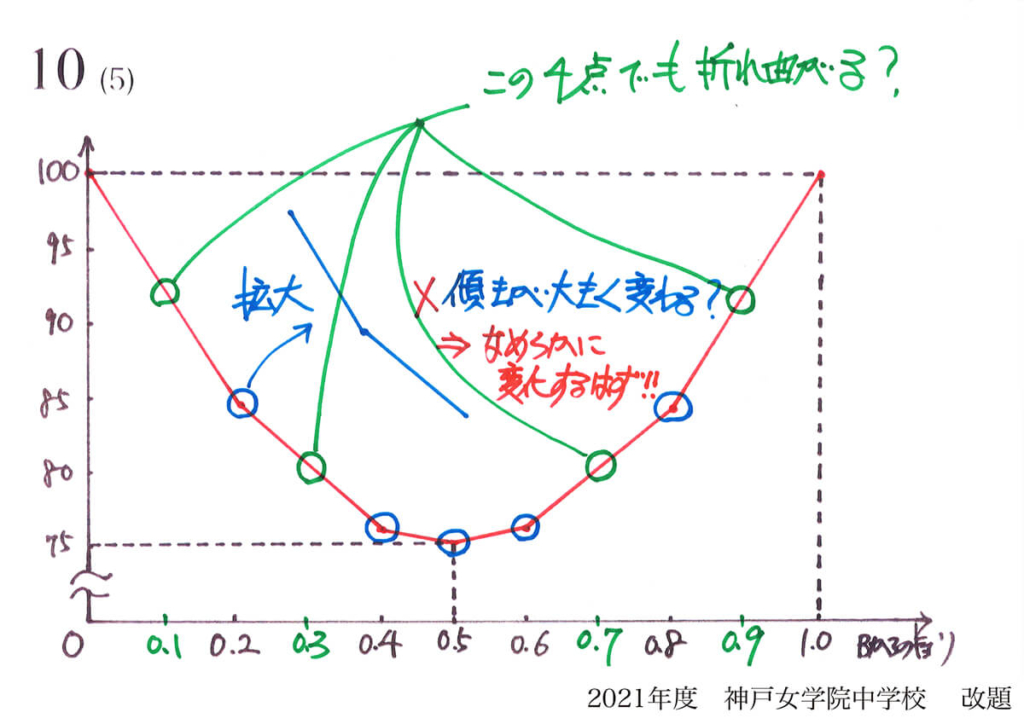
このグラフの横軸の各点の半分の位置に、もう一つ「折れ点」ができます。
女子小学生直線だったところが、
折れ線になると・・・
女子小学生点をどんどん増やしてゆくと、
だんだん線がなめらかになる！
このように、「折れ点を増やしてゆく」となめらかになります。
自分で描いてみましょう。
男子小学生カックンカックンしていたのが、
細かくなると、なめらかになるね。
男子小学生ちょっと
面白いかも！
「動く点は難しい」と感じることは多いです。
ここで、「動く点の気持ち」になって、「自分が動く点になってみる」イメージも良いでしょう。
「面白い」と思うと楽しいですし、「面白い」と感じたことは記憶に残るので非常に良いことです。
自分で状況を変えて考える：具体的にイメージ
このように、算数や理科で分かりにくい時は、自分で状況を具体的に考えましょう。
あるいは、今回のように「もう少し細かい分割だったら」と考えてみましょう。
男子小学生自分で勝手に考えても
良いの？
「問題の条件・状況が変わるほど、大きく変更する」のでなければ、良いです。
女子小学生自分で色々と具体的に
考えると、よく分かる気がする！
自分の分かりやすいように、考えやすいように考えてみましょう。
次回は下記リンクです。
