前回は「グラフを描いて「分からない」から「分かる」ポイント〜状況のイメージとグラフのだいたいの形・傾きと変化の仕方・なめらかにつなぐ・連続的に変化するイメージ・問題10(5)解法〜」の話でした。
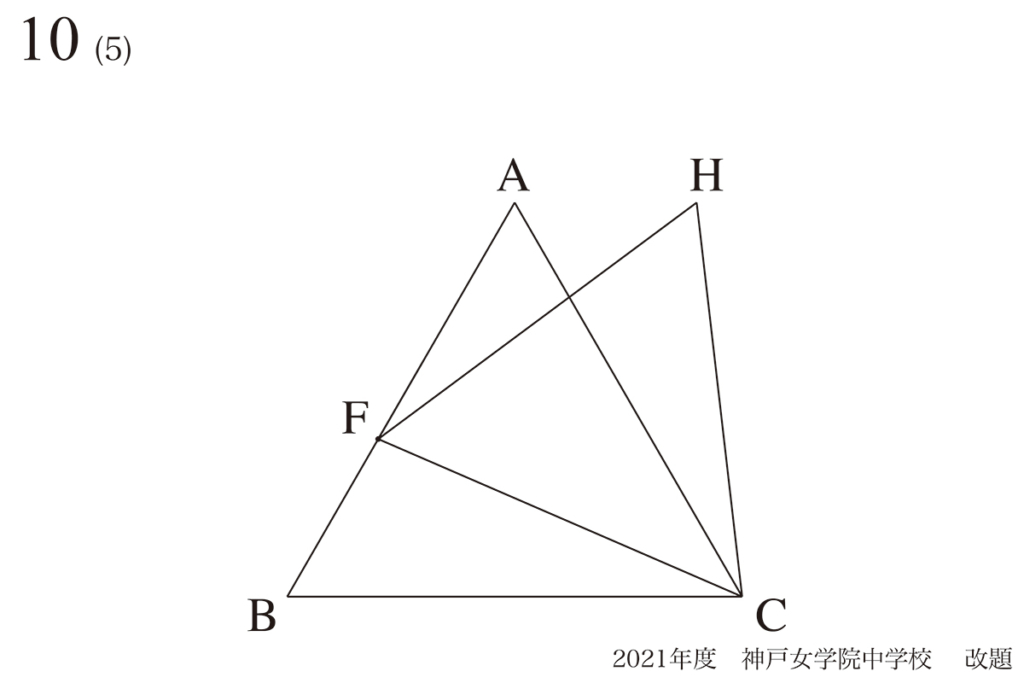
問題10(5)再掲載

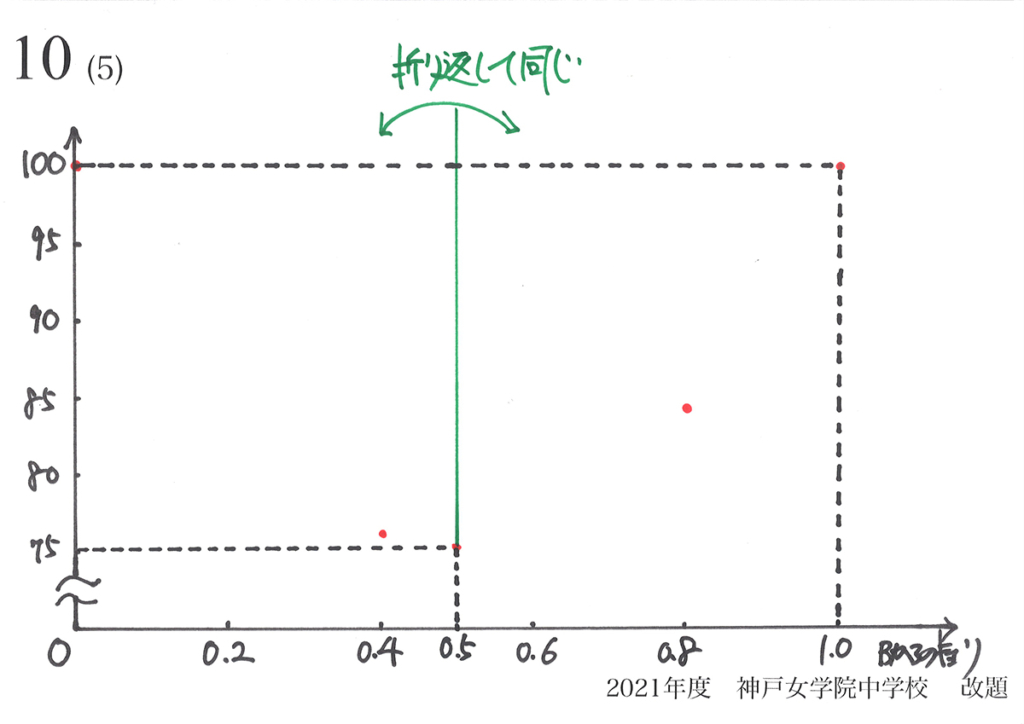
グラフの読み取りのポイント・コツ:図形と現象の対称性
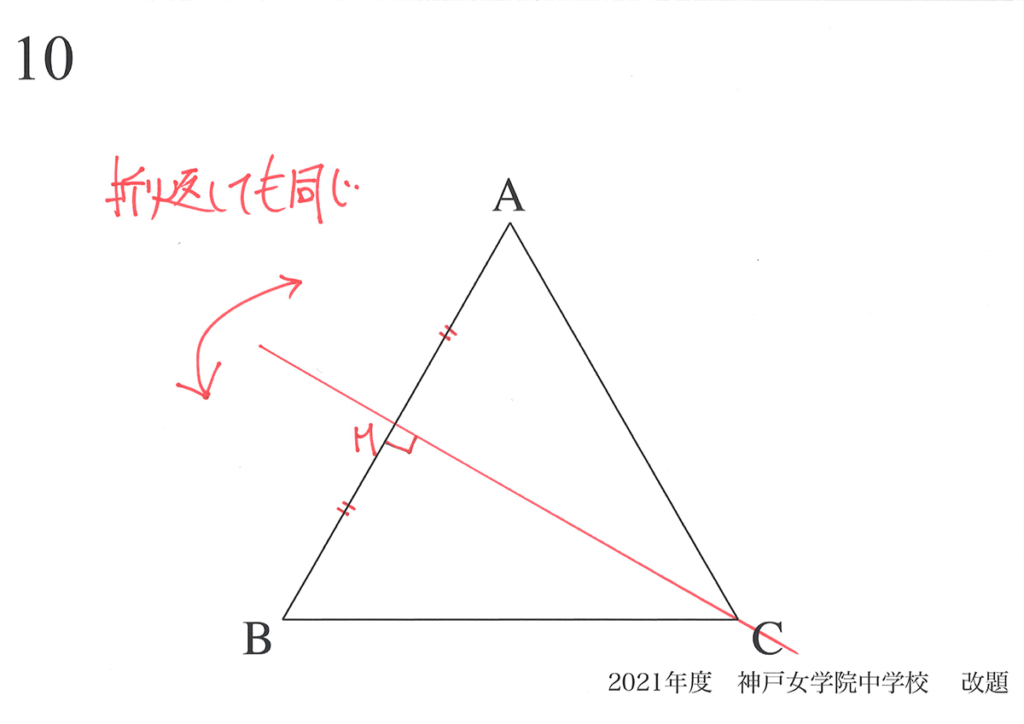
図形の対称性から「グラフの対称性」を考えて、グラフの大体の形を考えました。
逆に「グラフに(およその)対称性」があるときは、対象とする図形や現象に「対称性がある可能性」があります。
・図形に対称性がある時、グラフにも対称性がある
・グラフに(およその)対称性がある時、対象とする図形や現象に「(およその)対称性がある」可能性が高い
「図形の対称性→グラフの対称性」に対して逆の場合は、少し注意が必要です。
「グラフの(およその)対称性→図形・現象の(およその)対称性」です。
なぜ、こっちは(およその)が
つくの?
それは、理科の実験などは「誤差がある」からです。
実験や現象を対象とする場合は、対称・繰り返しがあっても「グラフがピッタリ対称」にはならない傾向があります。
そっかあ・・・
でも、何か「対称」とか「繰り返し」を見つけたら、大事だね!
グラフが「分かる」姿勢:大雑把に考える
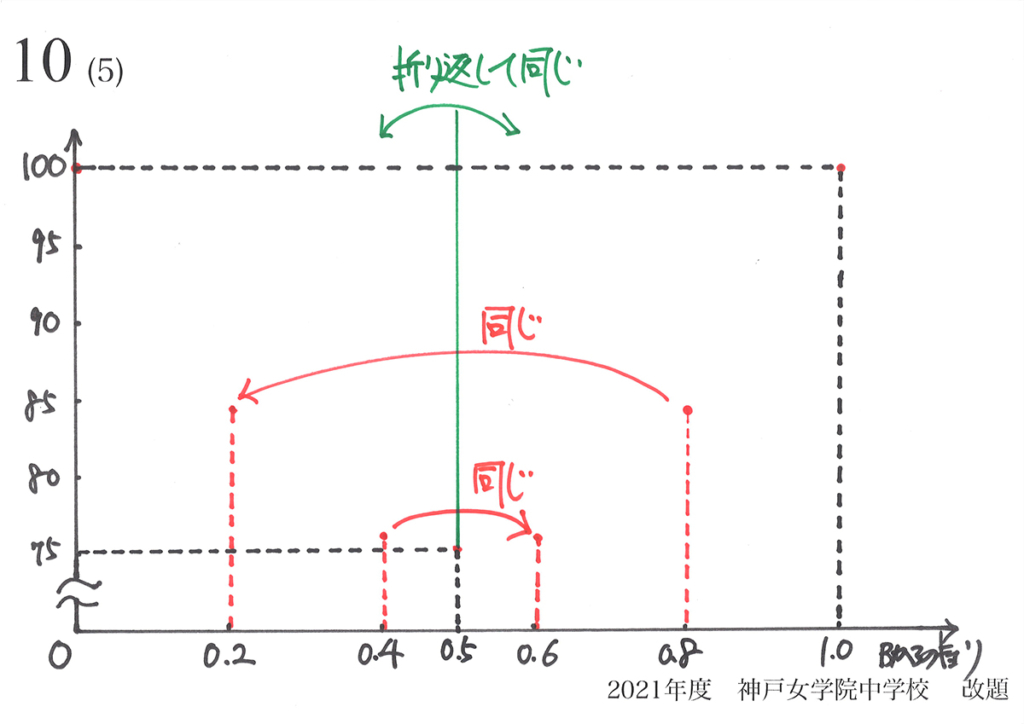
今回は「寄り道」で分かった面積76,84が、小問等でなく「分からない」場合を考えましょう。
この場合は、動点Fが点A,Bと中点Mにある時しか、面積が分かりません。
それじゃ、
グラフは描けないんじゃない・・・
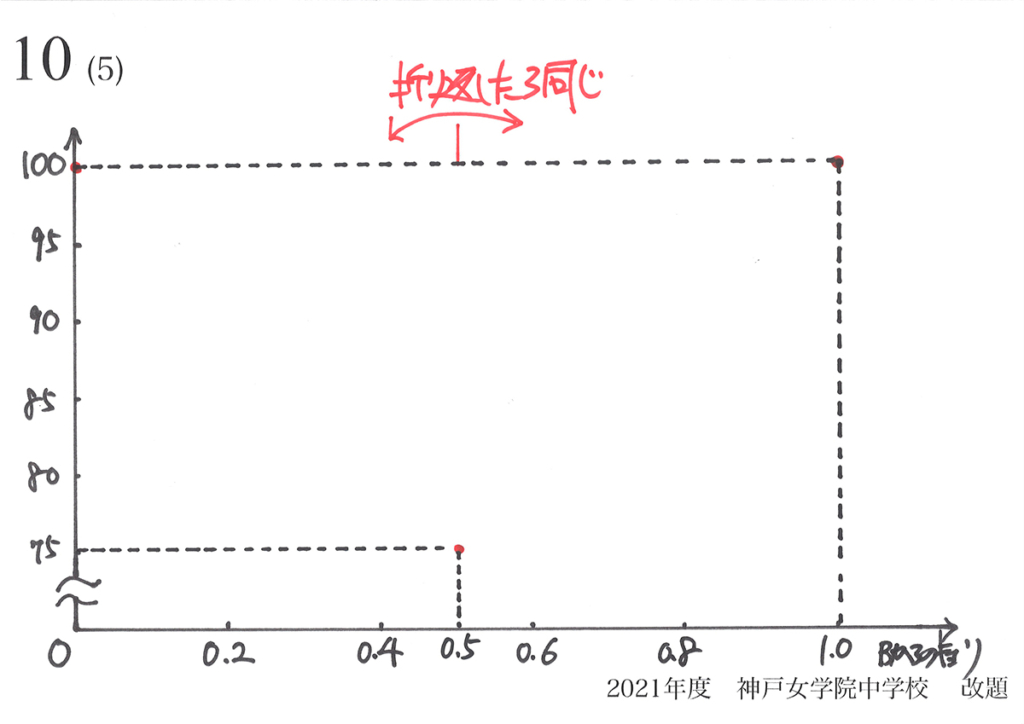
「動点Fが点A,Bと中点Mにある時」は、正三角形FCHの面積が「最大と最小となる時」です。
ここで「図形の対称性→グラフの対称性」を考えましょう。
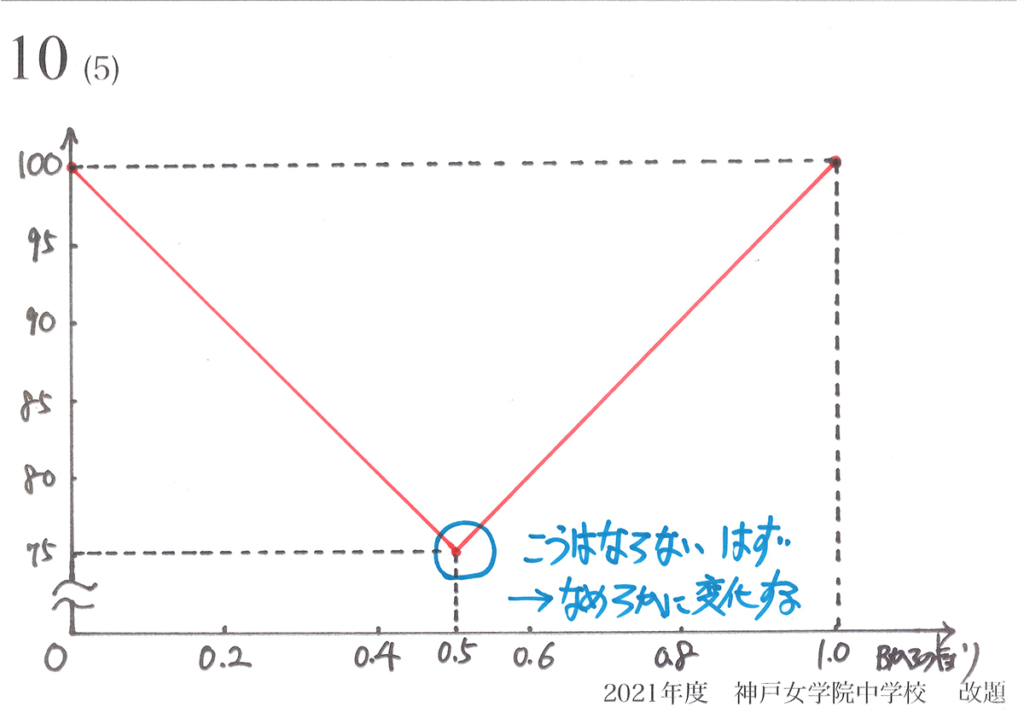
各点を直線でつないでみると、上のグラフのようになります。
こうはならないと
思うよ!
こんなに急な変化の
グラフって、なかなかないよね・・・
なんか変だし・・・
一番小さいところ(最小)で
尖っているのが変な感じ・・・
「大体分かる」ことも大事に:図形や現象の変化をイメージ
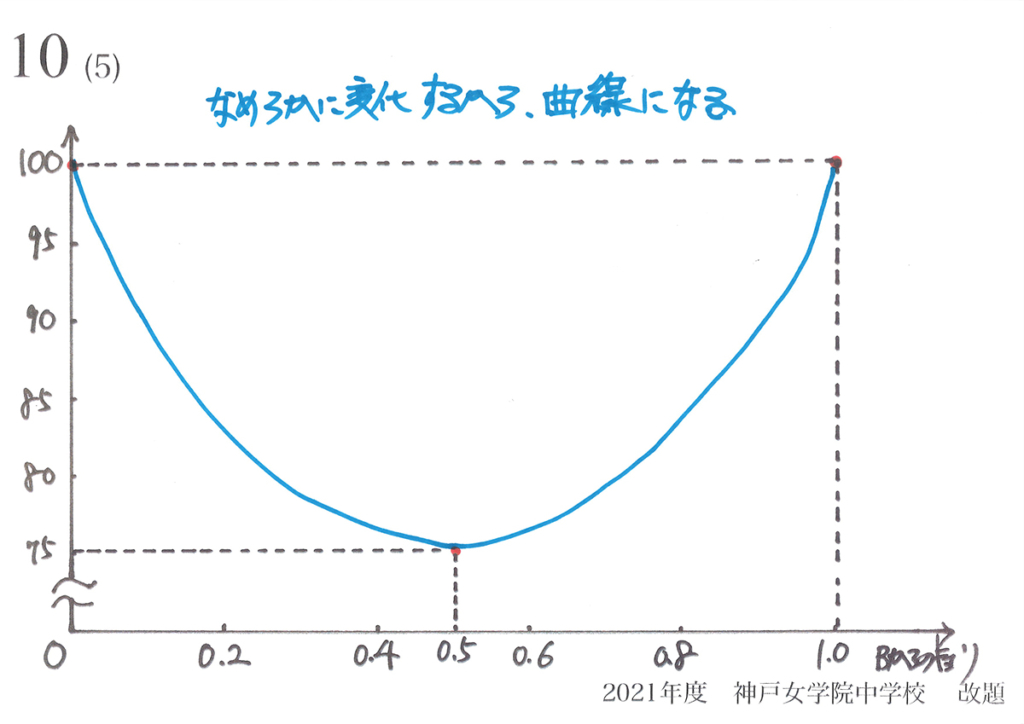
この場合、「急激に変化せず、なめらかに変化するはず」ということを考えましょう。
正三角形の辺FCの長さは、「点FがAからMに移動するにつれて、徐々に小さくなる」です。
このことをイメージしましょう。
すると、途中の点の数字が分からなくても、「大体の大雑把な形」は分かります。
この「大体」が算数・理科では、非常に大事です。
「大体の感じをつかむ」ことを気にしながら、学んでゆきましょう。
「だいたい」でも
良いの?
「だいたい」分かることは大事です。
算数でも理科でも、「全然分からない」ではなく「だいたい分かる」ことも大事です。
まずは「なんとなく分かる」ことも大事にしましょう。
「分かること」に自信持つようにしましょう。
そして、「分からない部分」や「理解できない箇所」を少しずつ学んでゆきましょう。
次回は下記リンクです。



