前回は「グラフを描く・理解するのが得意になるポイント〜図形の対称性・点をつないでグラフを描く・状況をイメージ・問題10(5)解法〜」の話でした。
問題10(5)（再掲載）
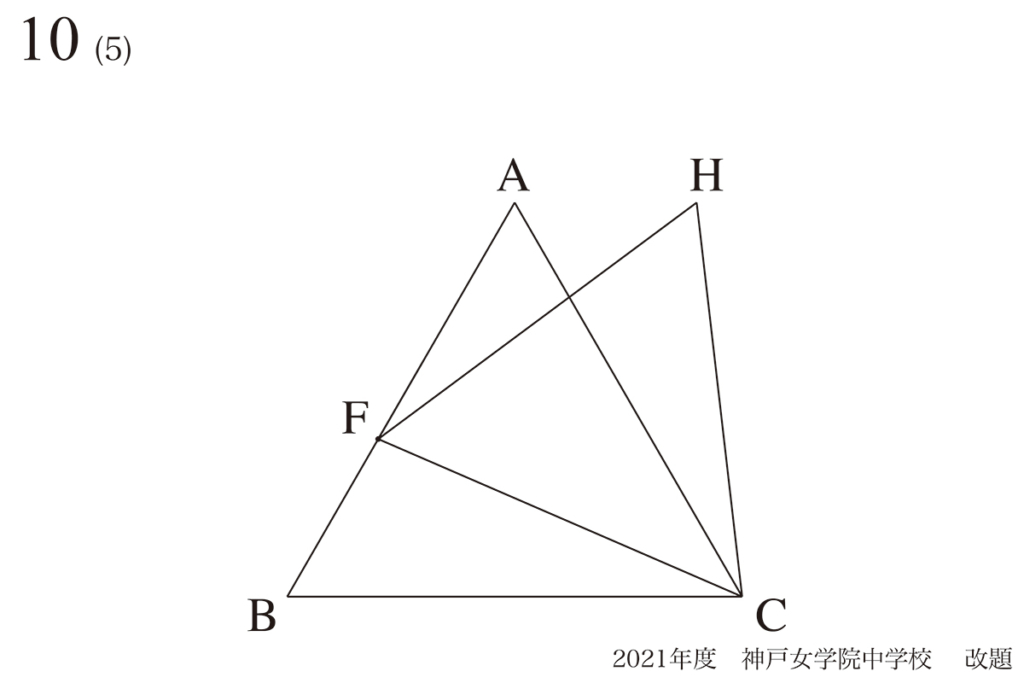
状況のイメージとグラフのだいたいの形：傾きと変化の仕方
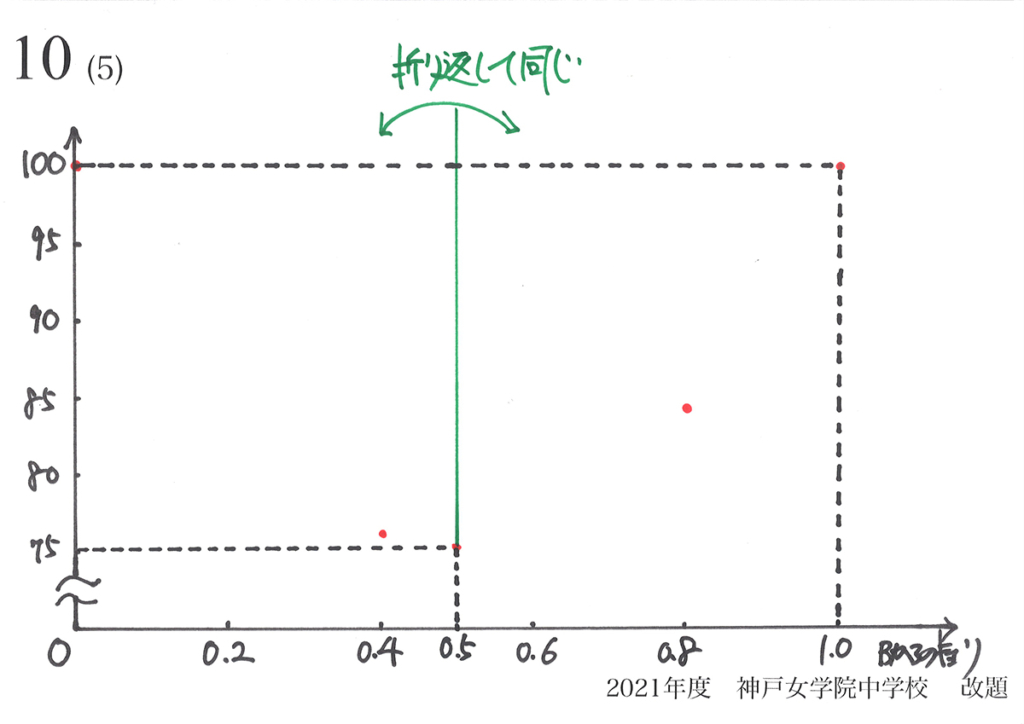
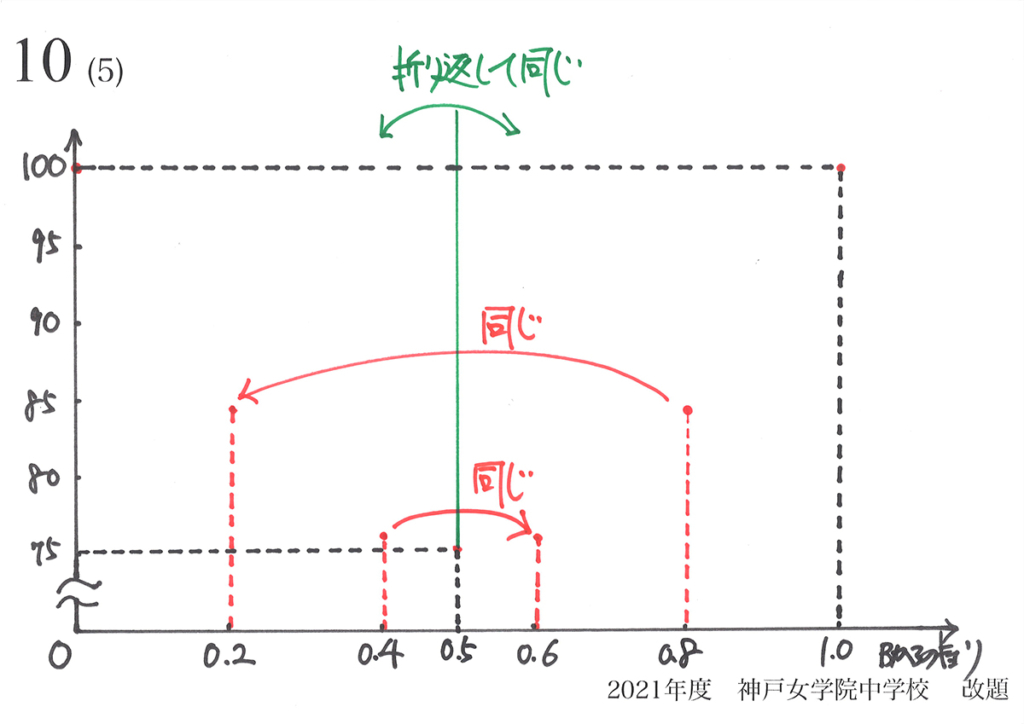
図形の対称性から、グラフに対称性があることが分かりました。
これで、グラフの大体の形が見えてきました。
点同士を結んで、グラフを描いてみましょう。
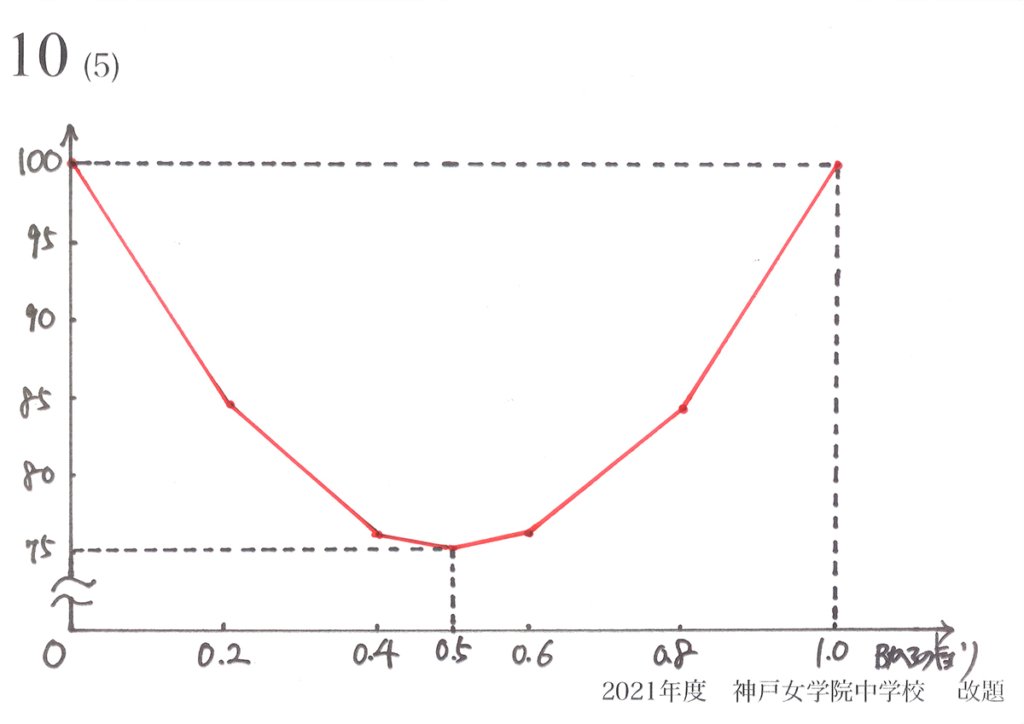
図形の大体の形として「折れ線グラフ」になります。
各点の前後で、「カックンカックンしている」ことを考えましょう。
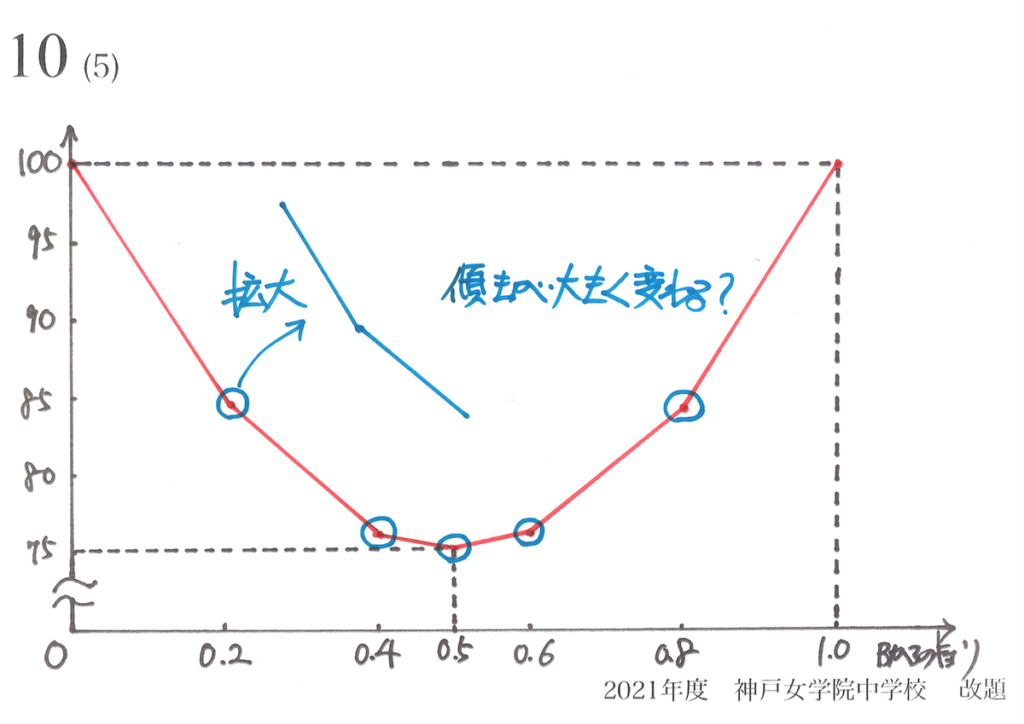
それぞれの点の前後で「傾きが大きく変化」しています。
グラフでは「最大・最小」の状況と「直線（曲線）の傾き」が重要です。
・最も特徴的な「最大・最小」の状況
・直線（曲線）の傾きと傾向
男子小学生「直線の傾き」は分かるけど、
「曲線の傾き」って分からない・・・
「曲線の傾き」に関しては、「大体の傾向」と考えましょう。
「傾き」と「傾向」は、共通した字があります。
女子小学生確かに「大体の傾向」が
大事な気がする！
矢印の考え方だと、「正三角形が次々に（連続的に）作られてゆく」のが分かります。
カックンカックンしている部分を拡大すると、
女子小学生なんか
変だね・・・
男子小学生正三角形が次々出来るから、
もう少しなめらかな感じになるんじゃない？
こんなに急激に変わらないで、なめらかに変わりそうです。
理由がわからなくても 「何か変」という気持ちを持つことを大事にしましょう。
それは、「状況をイメージ」して「グラフの大体の形を考える姿勢」です。
なめらかにつなぐ：連続的に変化するイメージ
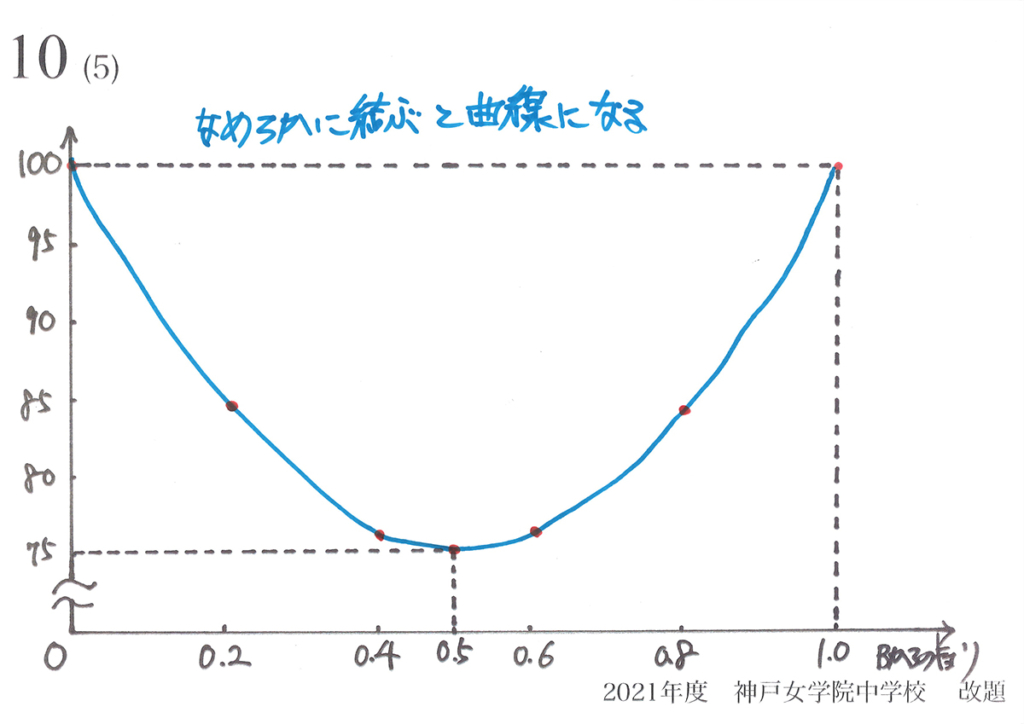
それでは、各点をなめらかにつないでみましょう。
曲線になります。
男子小学生あっ、
本当だ！
女子小学生きれいな
曲線だね！
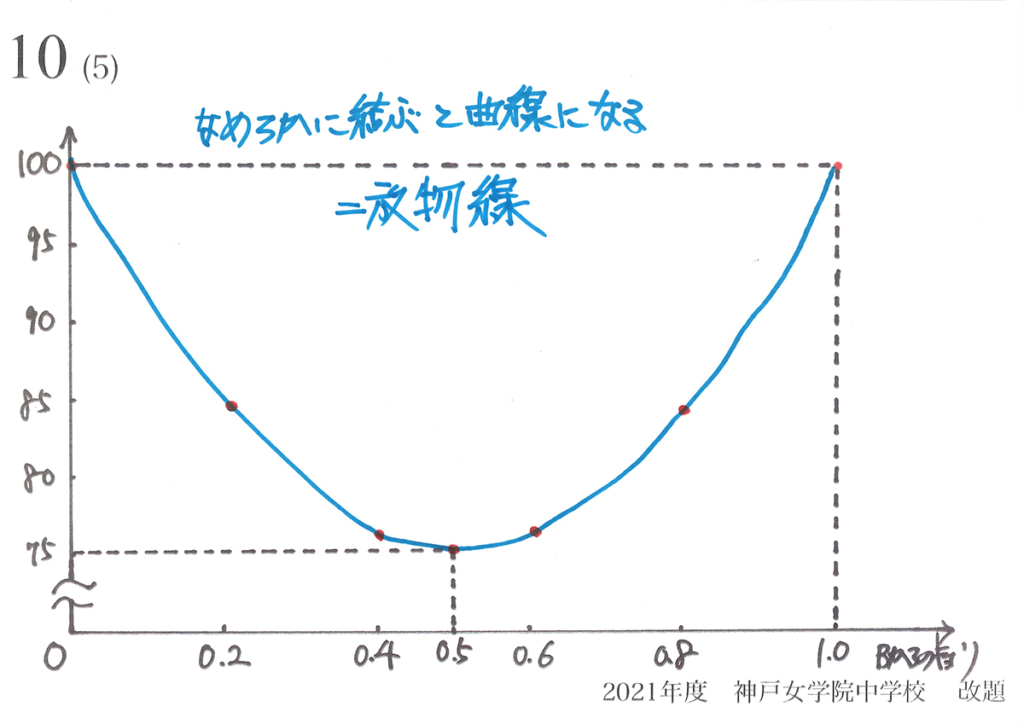
この曲線は「放物線」と呼ばれています。
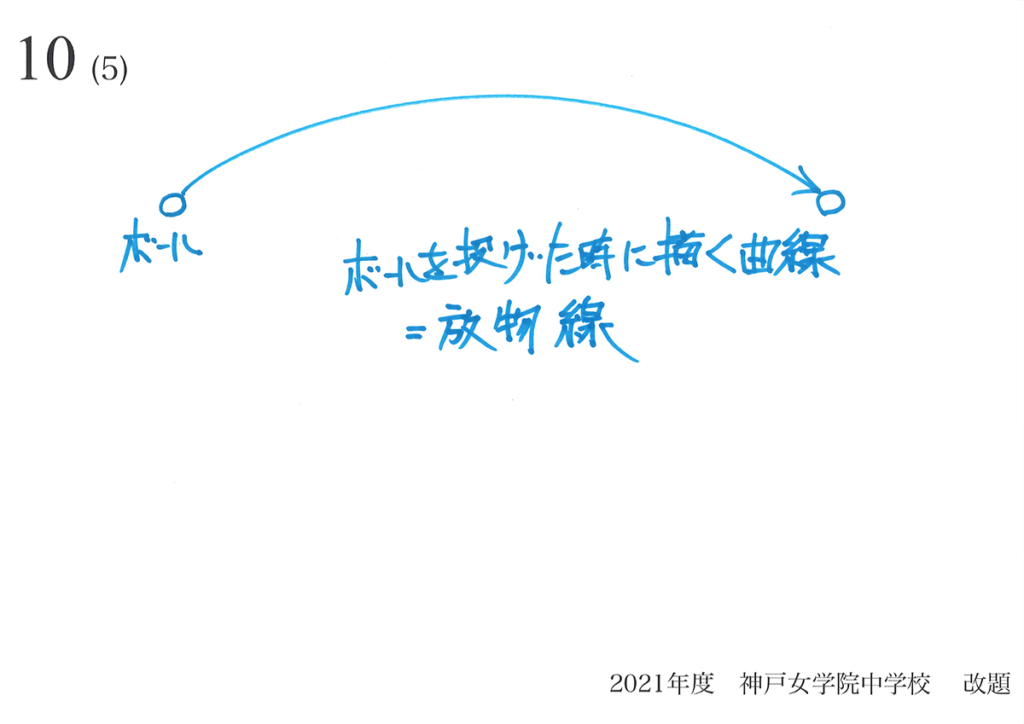
校庭でボールを投げると、「ポーン」と曲線を描きます。
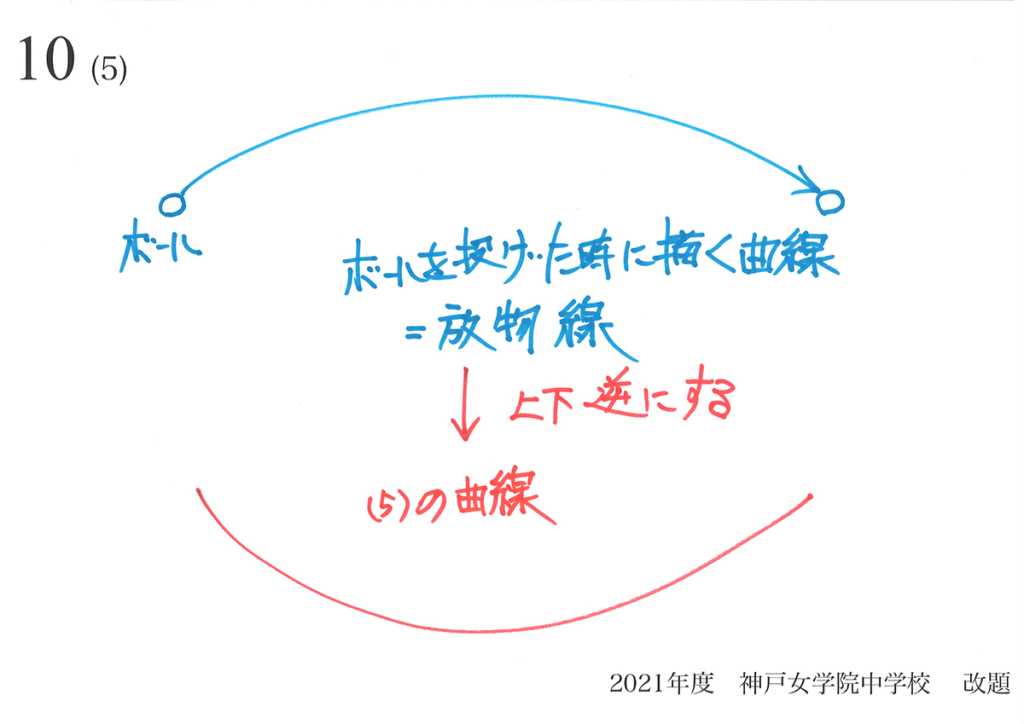
この放物線を上下逆にした曲線が、今回のグラフの形です。
小学校の範囲外ですが、校庭でボールの動きを楽しんで見てみましょう。
男子小学生今度、友達と野球するときに
ボールの動きを見るね！
この問題のポイントは、グラフを描くだけではなく、「理由を書くこと」でした。
・横軸の中点で対称性がある（折り返したら同じである）こと
・各点のところで（前後で）なめらかにつながること
これらの性質を「自分の言葉」で書くと良いでしょう。
今回の問題は、小学生の範囲を超えています。
そのため、「これは必要ない」と考える方もいらっしゃると思います。
ご参考として、お読みいただければ幸いです。
次回は下記リンクです。
