前回は「平行の大事な性質と動点P〜平行な直線を見つけたら考えること・変わらない長さを活かす考え方・面積と長さの次元と次数・問題10(4)解法B〜」の話でした。
問題10(4)再掲載

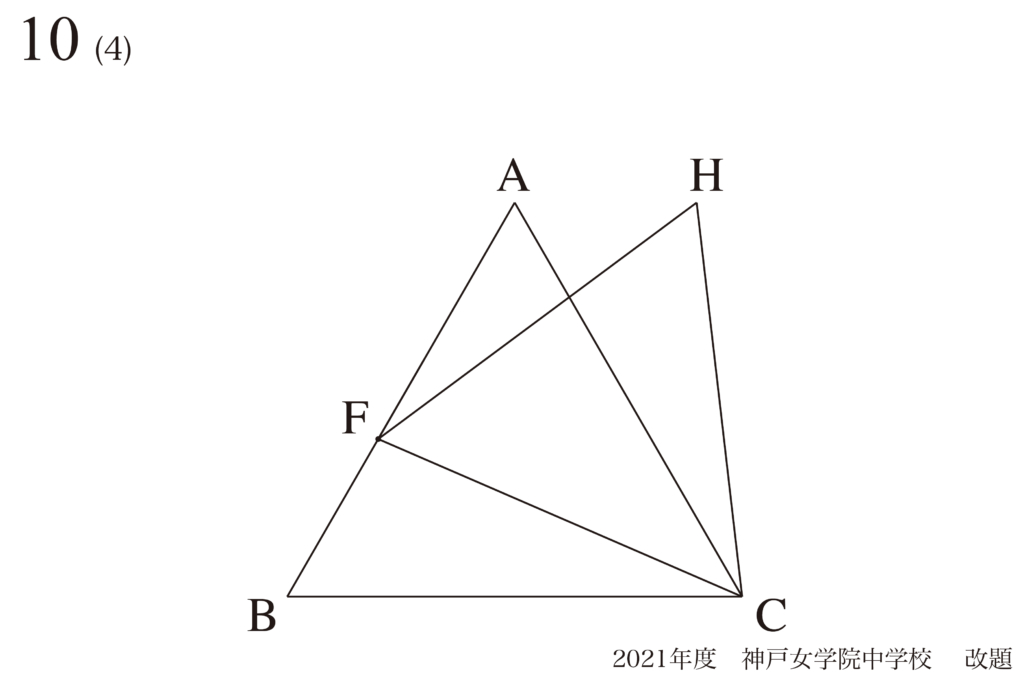
面積は「長さ・辺の比」:二次元と一次元
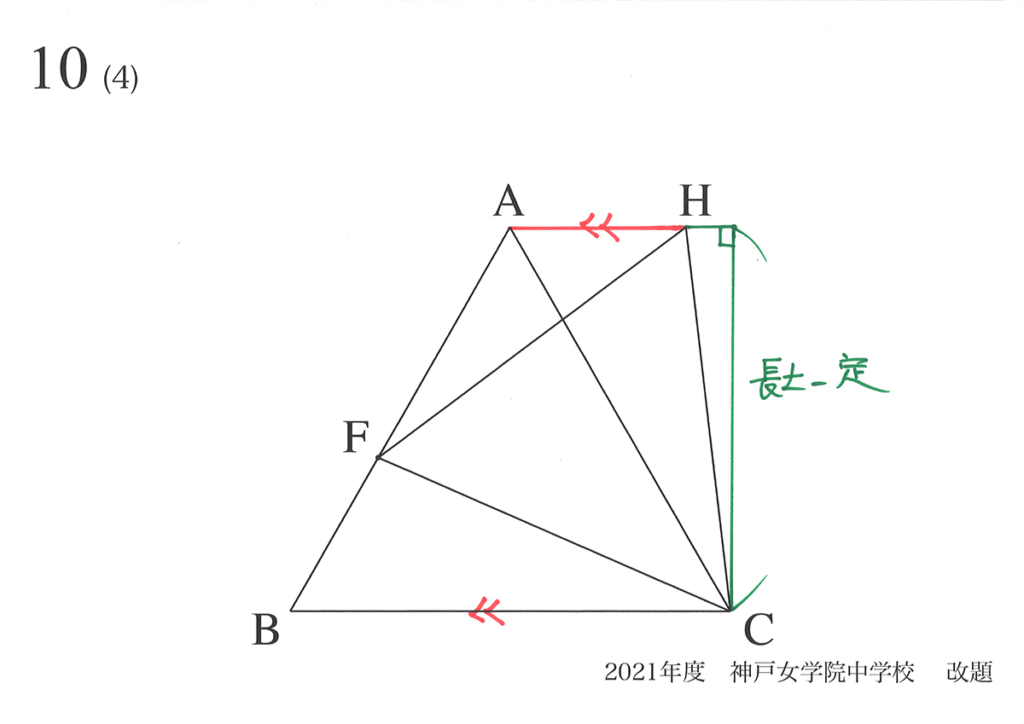
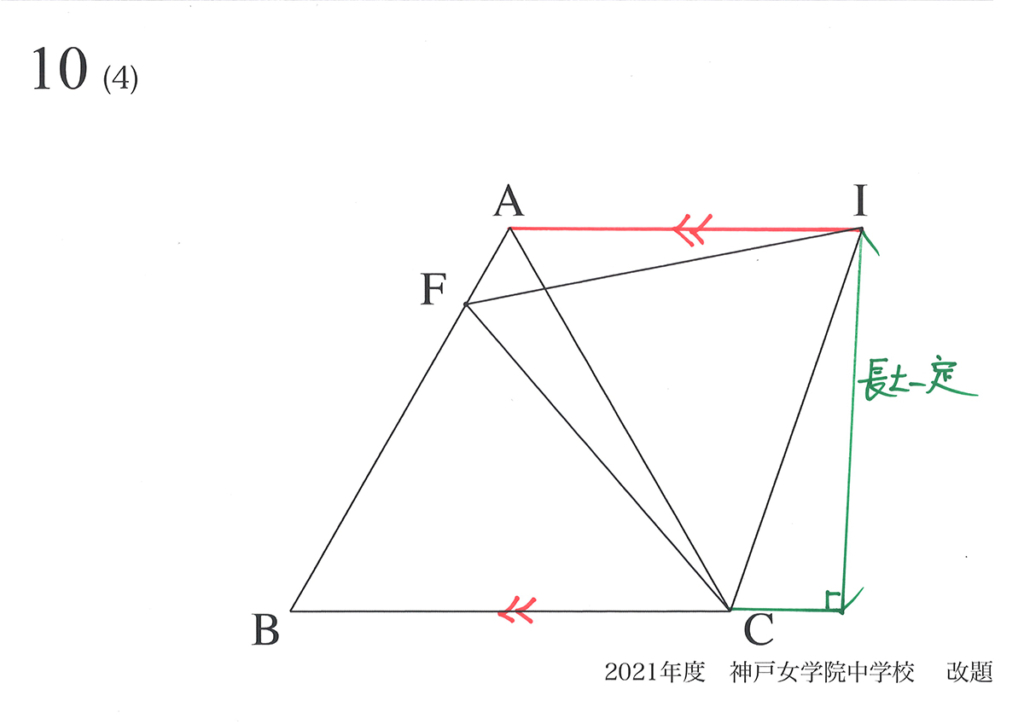
動く点Fが辺AB上を動く時、出来る正三角形の面積の最小値を考える時、「同じ長さ」に注目します。
・平行な直線同士の錯角は同じ
・錯角が同じ直線同士は平行
・平行な直線同士の長さ・距離は同じ(一定)
「同じ長さ」などは「問題を解く鍵」になることが多いので、見つけたら、
 男子小学生
男子小学生この性質を活用して
問題解けないかな?
「ヒントにならないかな」と考えましょう。
・変わらない(同じ・一定)の長さ・角度は、「普通ではない」大事な性質
・変わらない(同じ・一定)の長さ・角度を活用することを考える
「面積の最小値を考える」とは「面積を比較する」ことです。
そして、「比較する対象」は「次元・次数が小さい方が楽」です。
・長さは「cm」「m」など一次元
・面積は「cm2「「m2」 など、「単位に小さな2がつく」二次元
図形問題の「面積を求める」時は、大抵「辺の長さの比」を考えます。
そして、いくつかの「辺の長さの比」から「難しい面積も求まる」ことが多いです。
この時も、「面積を考えるときは、次数が一つ小さい辺の長さを考えている」ことになります。
・比較する対象の次元を小さくできないか、考える
・面積は「長さx長さ」で二次元、長さは一次元なので、一次元の方が簡単
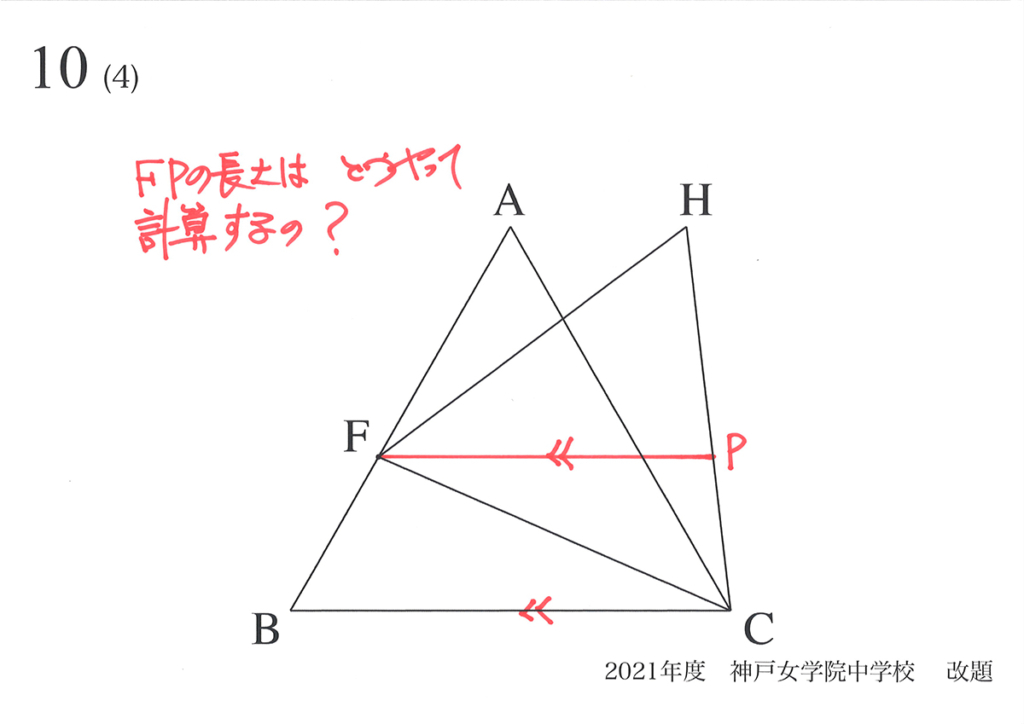

今回は、「正三角形の最小値」を考えるために、FPの最小値を図形的に考えてゆきましょう。
対称性から分かること:動く点と動画
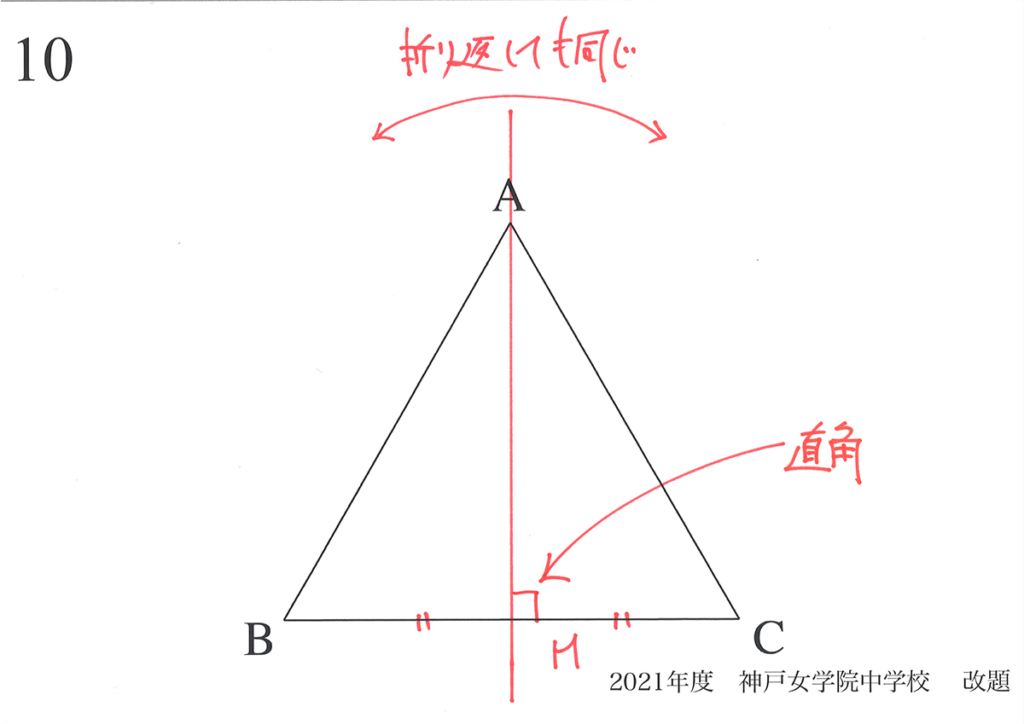

正三角形の対称性に関する話を、上記リンクでご紹介しています。
ここで考えたように、辺AB上の中点Mで折り返しても「同じ」です。
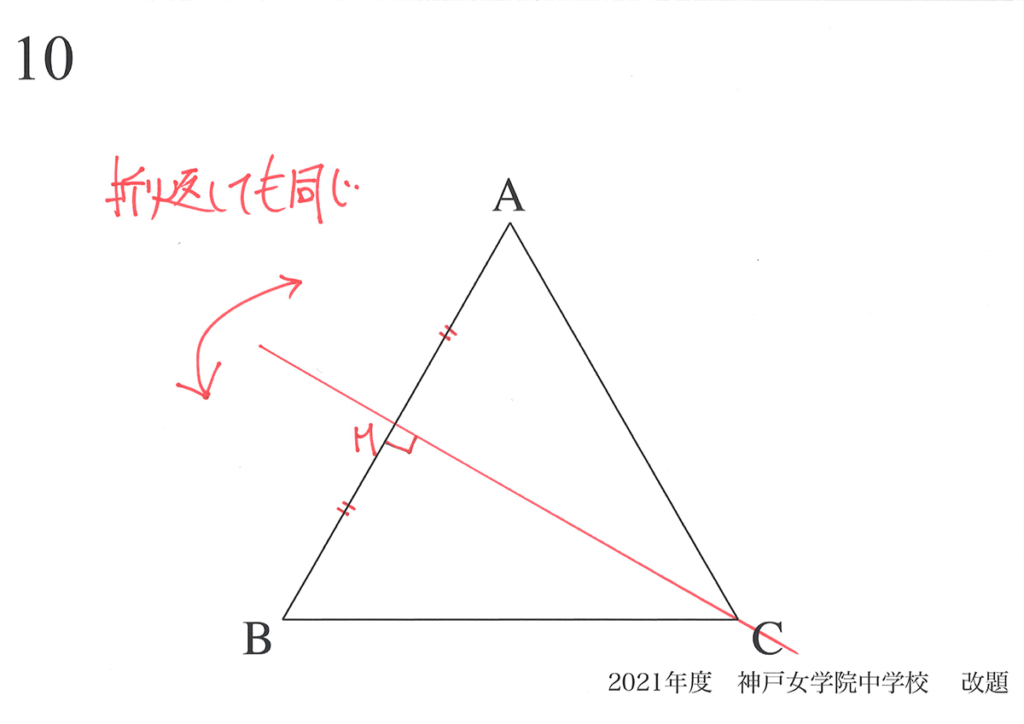

正三角形FCHの面積は、辺AB上を動く点Fが「BMにある時と、AMにある時が同じ」になります。
まず、「点FがBM上にある時を考えれば良い」と分かります。
点Fが、BからAに動いてゆく状況をイメージしてみましょう。



この「動く」のが
難しいよ・・・
「動く」は「辺AB上の全ての点を少しずつ動く」ので難しいです。
問題の図形は止まっているのに、「動画を考える」点が難しい理由です。
動く点が「連続的」ではなく「飛び飛びの位置を移動する」と考えてみましょう。
・1秒間に24枚の写真が連続的に映し出される(枚数は違う場合があります)
・1枚あたり1/24秒=約0.04秒なので、本当は「静止」しているのに、連続的に「動画」に見える
動画は実は「動いていない」のです。
実は「止まっている写真を高速で映写している」から「動いているように見える」だけです。
・連続的に、無限の点を移動するから難しい「動く点」
・代表的な点をいくつか選んで、具体的に描いてイメージする
・代表的、いくつかの点での状況(静止画)がたくさん並んで「動く点=動画」になるイメージ
点Fが頂点Aから中点Mに動いてゆく過程は、「点Fがある点を進むことの繰り返し」と考えましょう。
その過程と中点Mから頂点Bに動いてゆく過程を逆にした状況が「同じ」になります。
すると、、正三角形FCHの面積が最小となるのは



ひょっとしたら、
中点Mの時かも?
このように想像して、予測が出来ます。
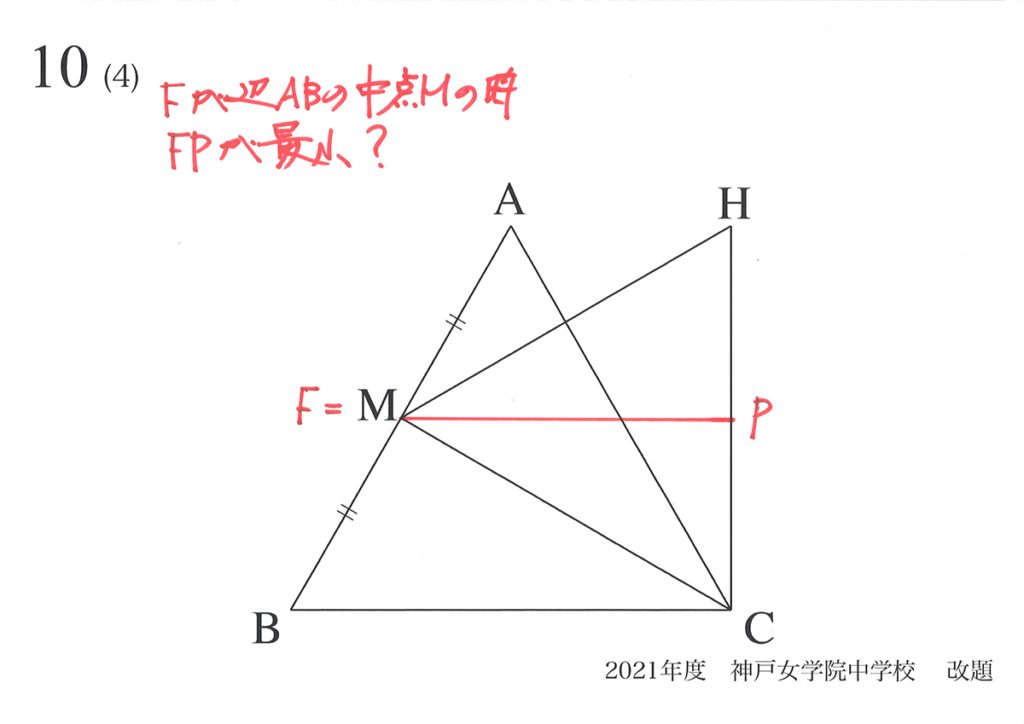

つまり、FPの長さが「Fが中点Mの時に最小となる」と予想できます。
予想を検証:垂線の性質
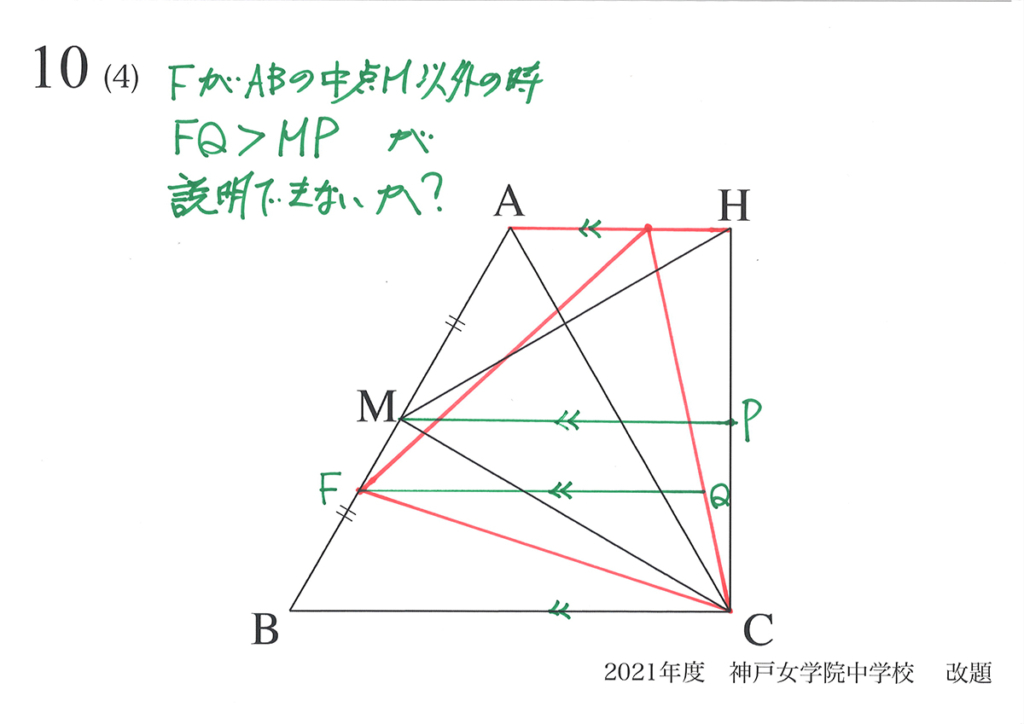

では、「F=中点Mの時、MPが最小」を検証・確認してみましょう。
そのためには、上の図のように描いてみましょう。
そして「F中点Mの時、そうでない時」の「FPを長さ」を図形的に考えてみましょう。
矢印の話から「AH、MP、FQ、BCが平行」なことが分かります。
「平行」が出てくれば、相似形がたくさん見えてきますから、考えやすくなります。



平行がたくさんあると嬉しいけど、
たくさんありすぎだよ・・・



こんなにたくさんあると
混乱してしまう・・・
難しく考えすぎず、「注目する二つの線」を中心に考えましょう。
「図形的に最小・最大」を考えるときは、自分なりに「ある部分の長さ」を設定してみましょう。
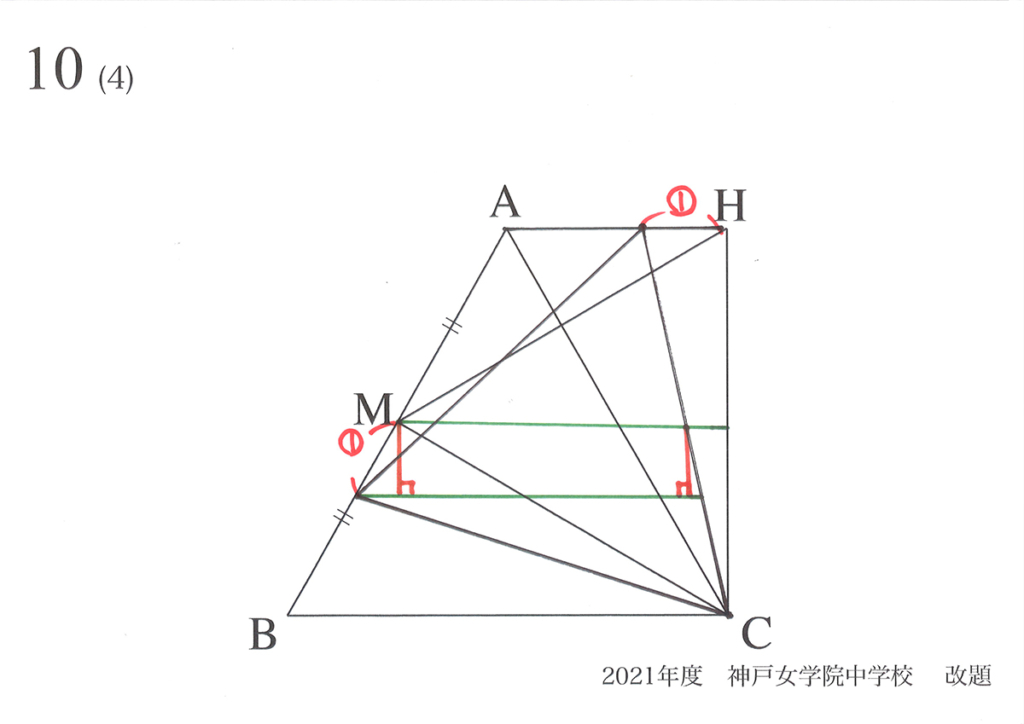

今回は、「点Fと中点Mの距離を①」と設定します。
これで、「F=中点Mの時、FPが最小」を考えてみましょう。
上図の垂線(垂直に下ろした線)がヒントです。
次回は下記リンクです。



