前回は「動点Pの問題が「できない」から「できる」へ〜変化しない量・長さ・モノに注目・2つのモノが動く時・変化しないモノは何か・問題10(4)解法A〜」の話でした。
問題10(4)再掲載
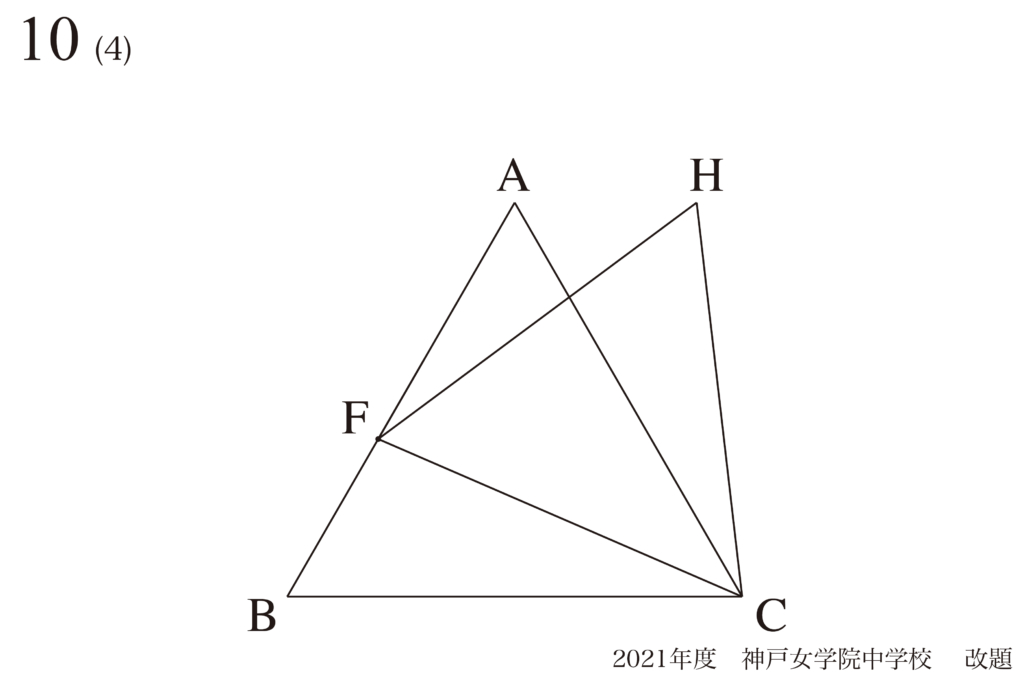
平行の大事な性質：平行な直線を見つけたら考えること
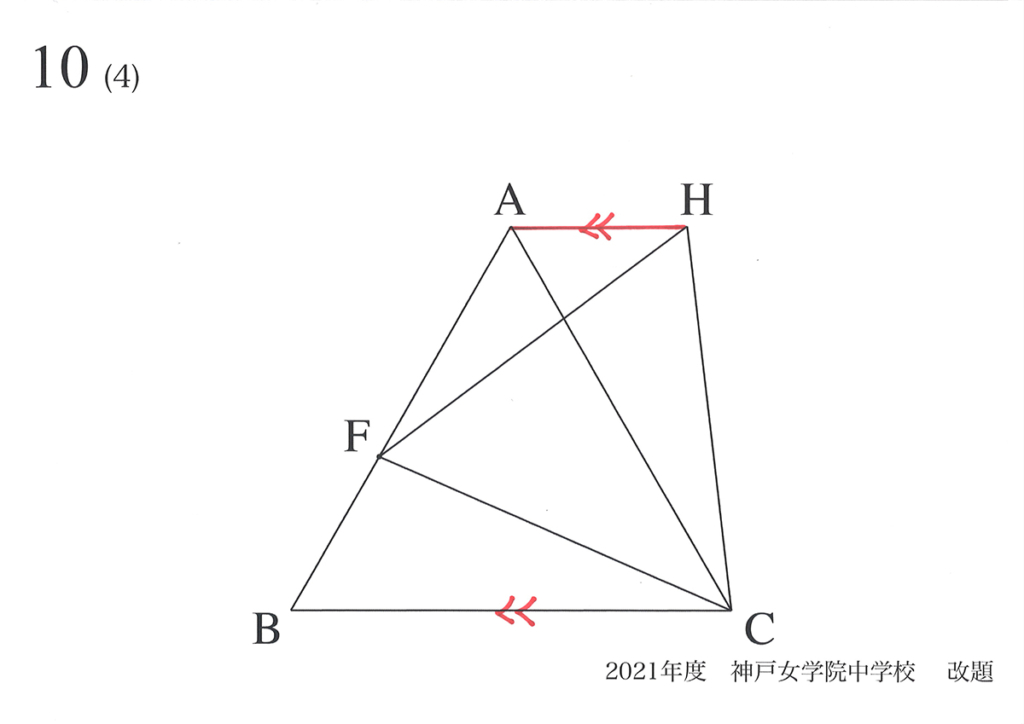
今回は、変わらないモノを考えて、この「正三角形の面積最小」を考えましょう。
変わらないモノを考えてみますが、「平行」がポイントです。
平行って、相似形が
たくさんできるね！
平行だと、
「お互いの線が交差しない」だよね。
「平行」にはもう一つ大事な性質があり、「平行な線の間の長さ・距離が一定」です。
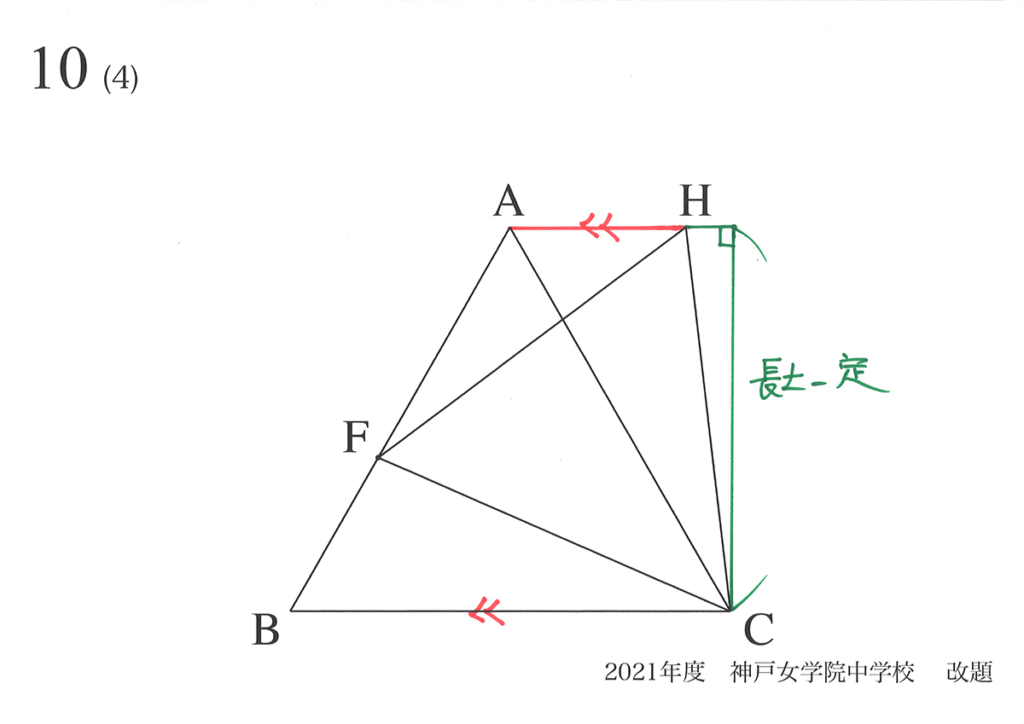
動点P（点F）の位置が変化しても、「平行な直線の間の長さは一定」です。
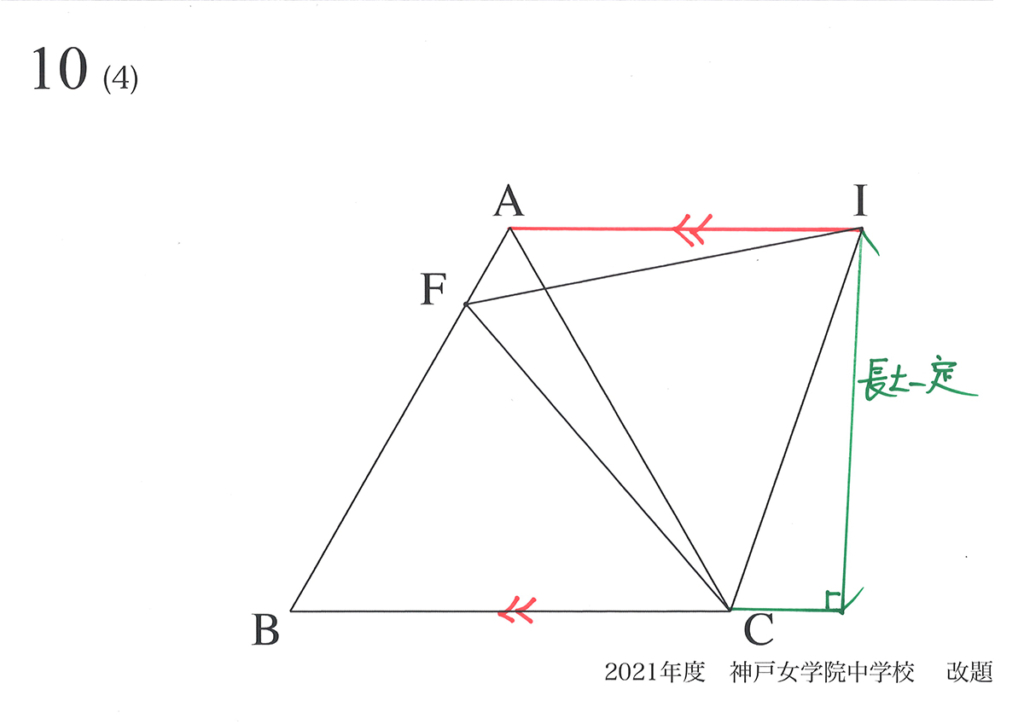
(1)(2)で考えた正三角形HFCも正三角形IDCには、「AH（AI）と BCが平行」です。
そのため、上の図の緑色の線の長さは同じ（一定、不変）です。
・変わらない（同じ・一定）の長さ・角度は、「普通ではない」大事な性質
・変わらない（同じ・一定）の長さ・角度を活用することを考える
このように「変わらない長さ」を発見したときは、
何か、これを使って
考えられないかな？
と考えるようにしましょう。
ここで、平行の性質の確認をしましょう。
・直線が互いに交わらない
・直線が互いに「全く同じ向き」を向いている
平行の直線は「決して交わらない」非常に特殊な直線の組み合わせです。
・平行な直線同士の錯角は同じ
・錯角が同じ直線同士は平行
・平行な直線同士の長さ・距離は同じ（一定）
そして、平行な直線があるときは、相似形がたくさんあることが大事な性質です。
・「相似形が必ずある」と考えて、相似形を探す
・相似形が見つからないときは、「相似形を作って考える」姿勢
変わらない長さを活かす考え方：面積と長さの次元と次数
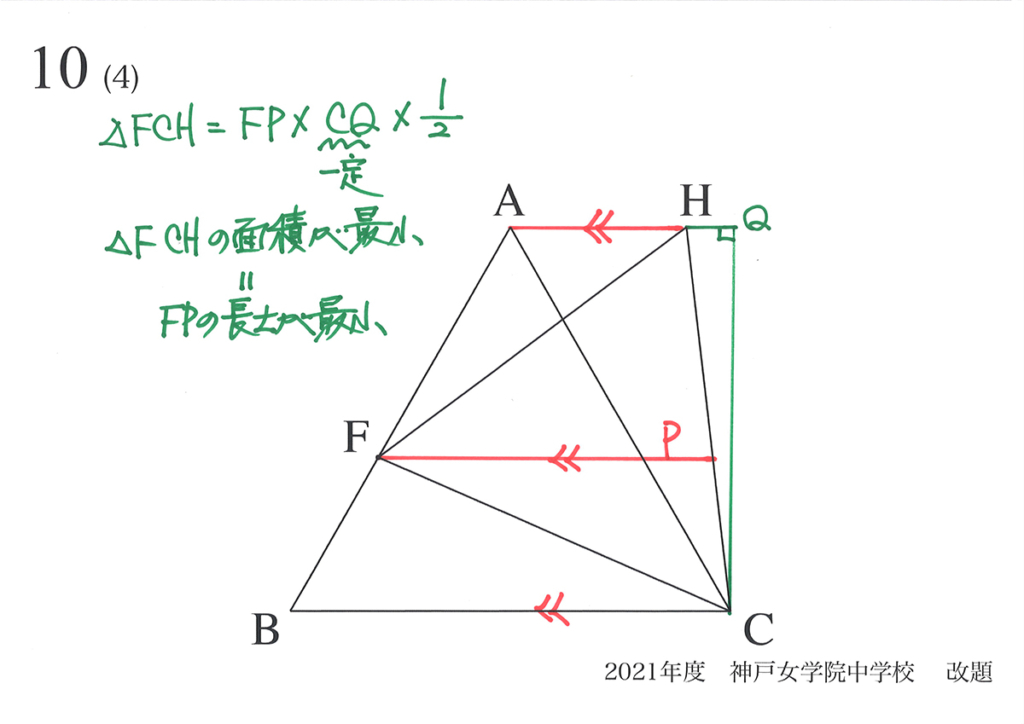
三角形の面積は「底辺x高さx1/2」です。
ここでは、「変わらない長さ」を使って面積を考えましょう。
上の図のように考えることができます。
これで、△FCHの面積が最小となる時は、図の「FPの長さが最小となる位置」です。
そっか！
これで、「面積を考える」が「長さを考える」になったね！
解法Aの時も「面積の比較」が「長さの比較」になって、
考えやすくなった。
・長さは「cm」「m」など一次元
・面積は「cm2「「m2」 など、「単位に小さな2がつく」二次元
算数や理科では「次元・次数を意識」すると良いでしょう。
「次元・次数」って
難しいけど・・・
言葉は難しく感じるかもしれませんが、面積では「平方センチメートル（メートル）」といいます。
この「平方」が二次元を意味します。
なんか、
少し分かった気がする。
・比較する対象の次元を小さくできないか、考える
・面積は「長さx長さ」で二次元、長さは一次元なので、一次元の方が簡単
確かに、「面積を比較」するより、
「長さを比較」する方が全然簡単だね！
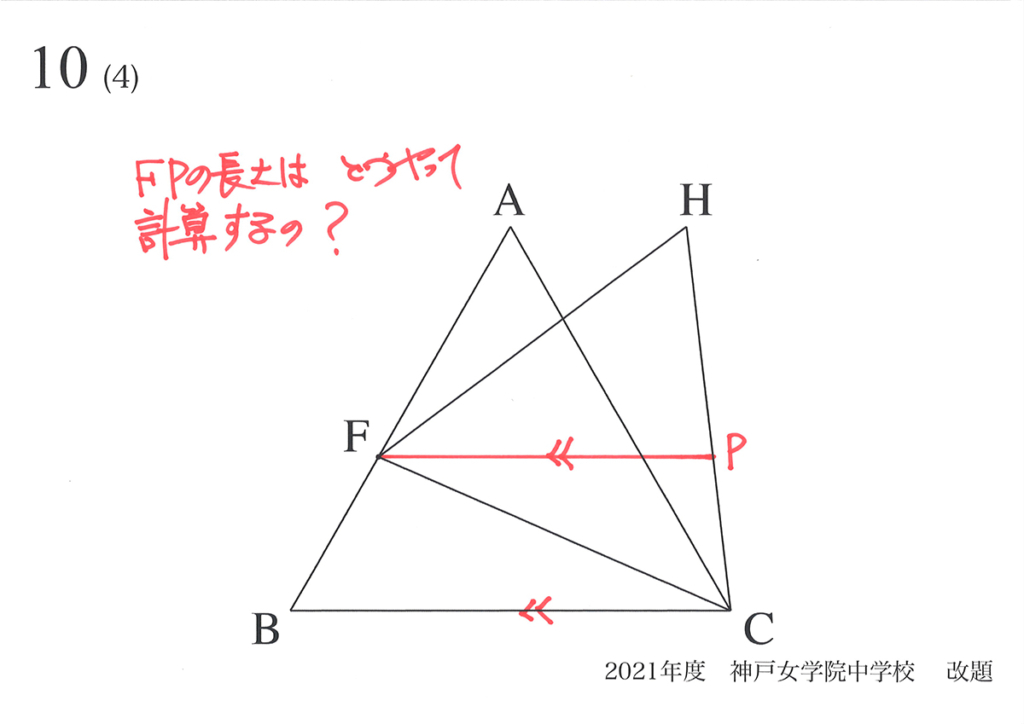
FPの長さをどうやって、考えれば良いかを考えましょう。
FPの最小値は、初等数学（中学2年程度）で比較的簡単に計算できます。
ここでは中学受験向けに、算数で考えてみましょう。
・解答に至らない「無駄なこと」が大事
・「遠回り」や「無駄」を経験すると、試験で「何が大事か」の感覚が磨かれる
少し難しいですが、手を動かしてみましょう。
