前回は「面積比を描いて理解して図形を得意に〜方眼紙のイメージ〜・面積比を計算して理解・四角形の相似形の面積比・大きい対象は小さく分割・問題10(4)ポイント〜」の話でした。
問題10(4)再掲載
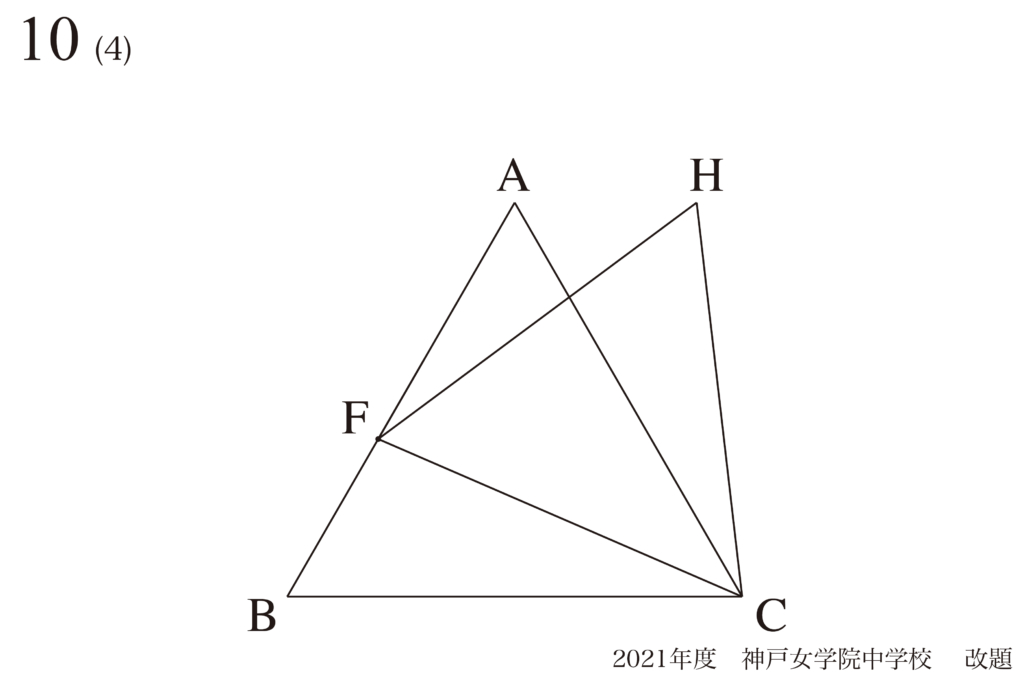
相似形を小さく分割
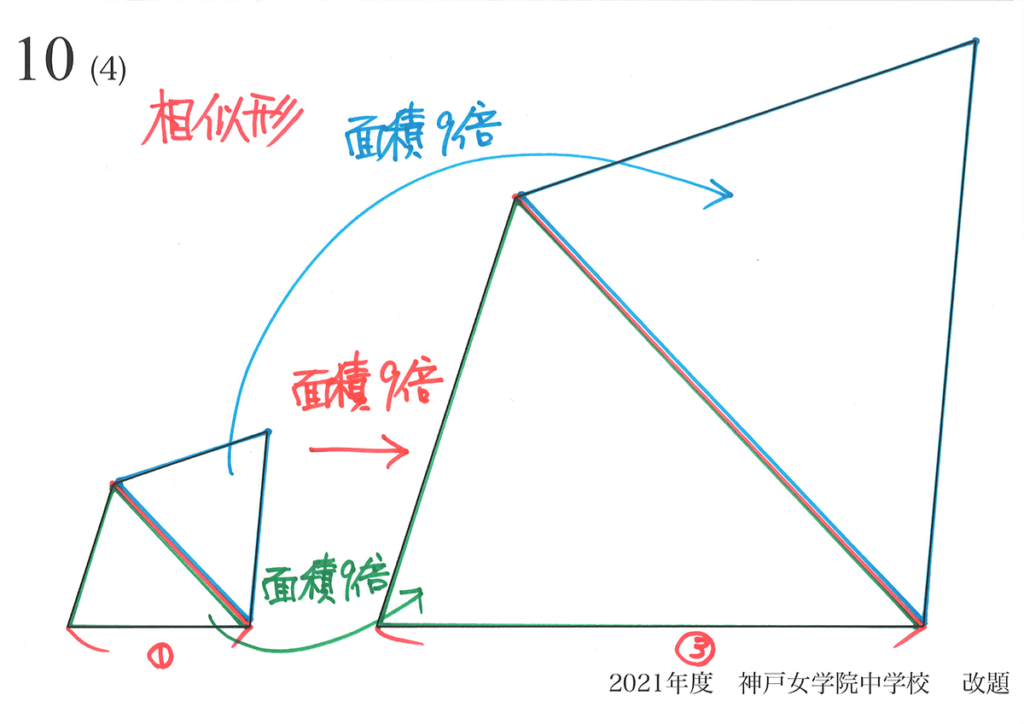
前回、「相似形の面積比=(辺の比)x(辺の比)」の具体的な説明の話をしました。
これは、辺の比が整数でなくても、小数でも分数でも成立します。
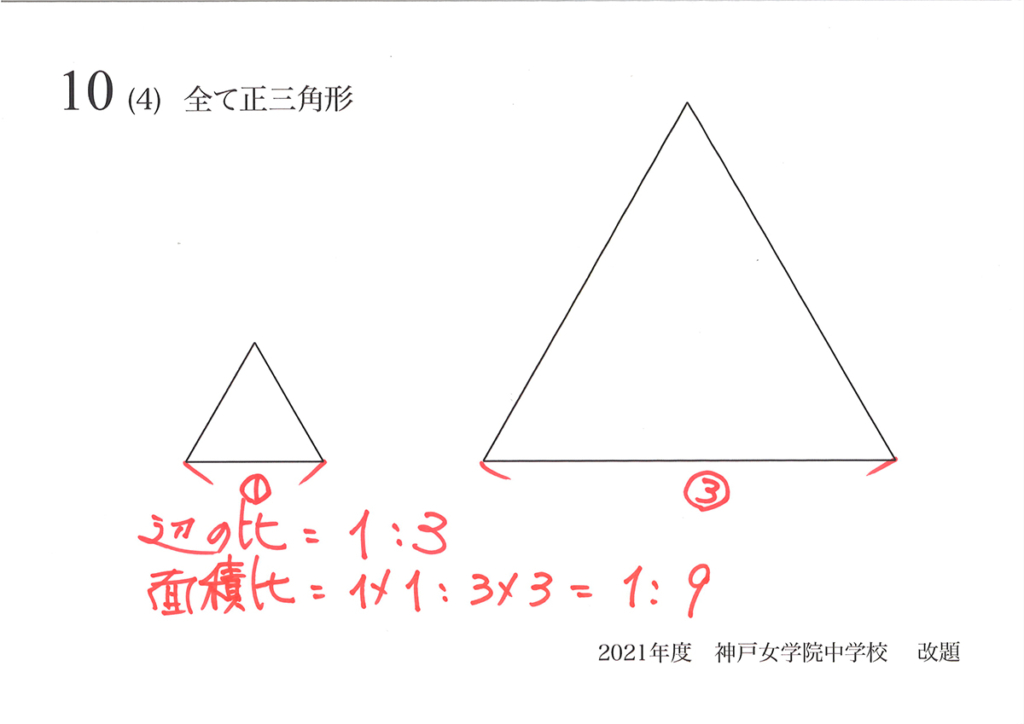
問題10は正三角形ですから、相似比=1 : 3 の正三角形を描いてみましょう。
大きい方の正三角形を、小さな正三角形で分割してみましょう。
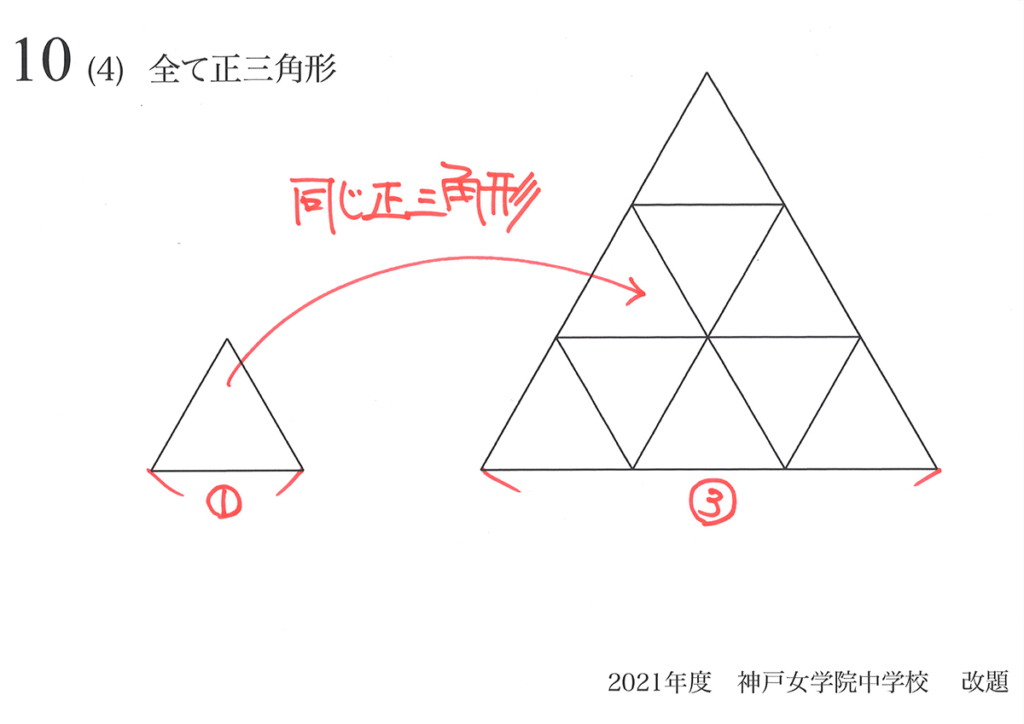
同じ正三角形がタイルのように、びっしり割れました。
これで「大きな正三角形=小さな正三角形 x 9」が分かります。
整数比の四角形等も、同じように分割できます。
ぜひ、自分で考えて描いてみましょう。
あっ、本当だ！
きれいに元の図形で分割できるね！
こうして考えてみると、
「相似比=辺の比 x 辺の比」がわかるね！
対象を小さく分割してゆくと、大事な性質が分かることがあります。
・大きい対象を小さくすると分かりやすくなる
・小さくすると「見えてくる大事な性質」がある
図形問題を解く時は、「大事な補助線を引く」ことばかりでなく、自分で色々と線を引いてみましょう。
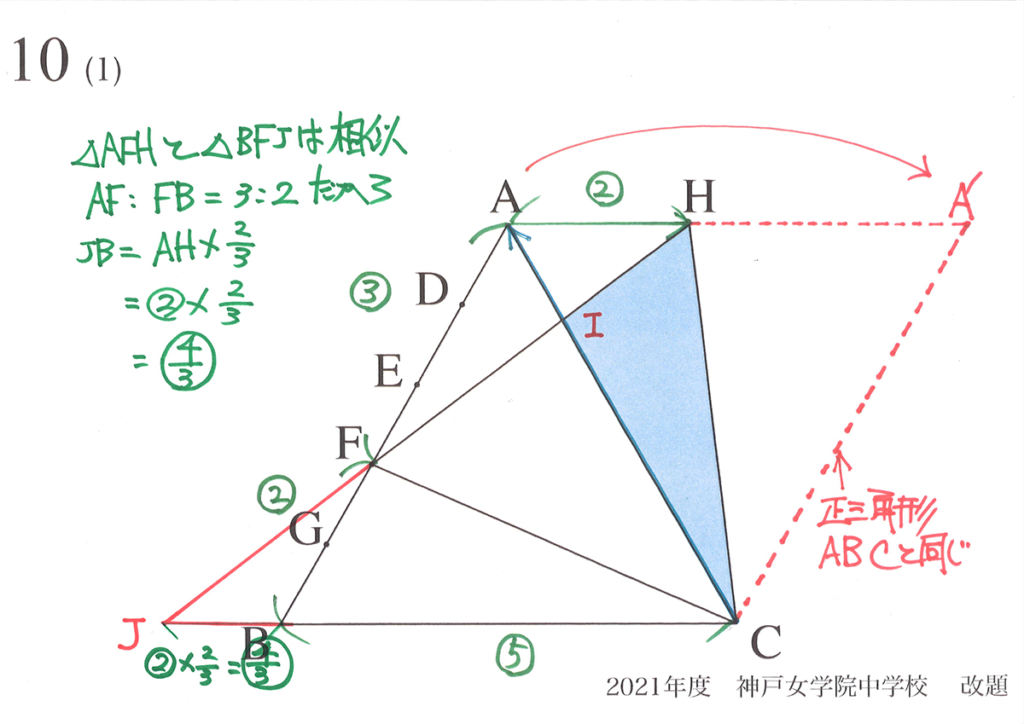
補助線が「図形の外に出てゆく」場合もありますが、「どちらかの相似形は元の図形の一部分」であることが多いです。
「図形を分けてみること」は、問題を解く鍵が見つかることがあるでしょう。
分割の数を考える：代数と幾何の接点
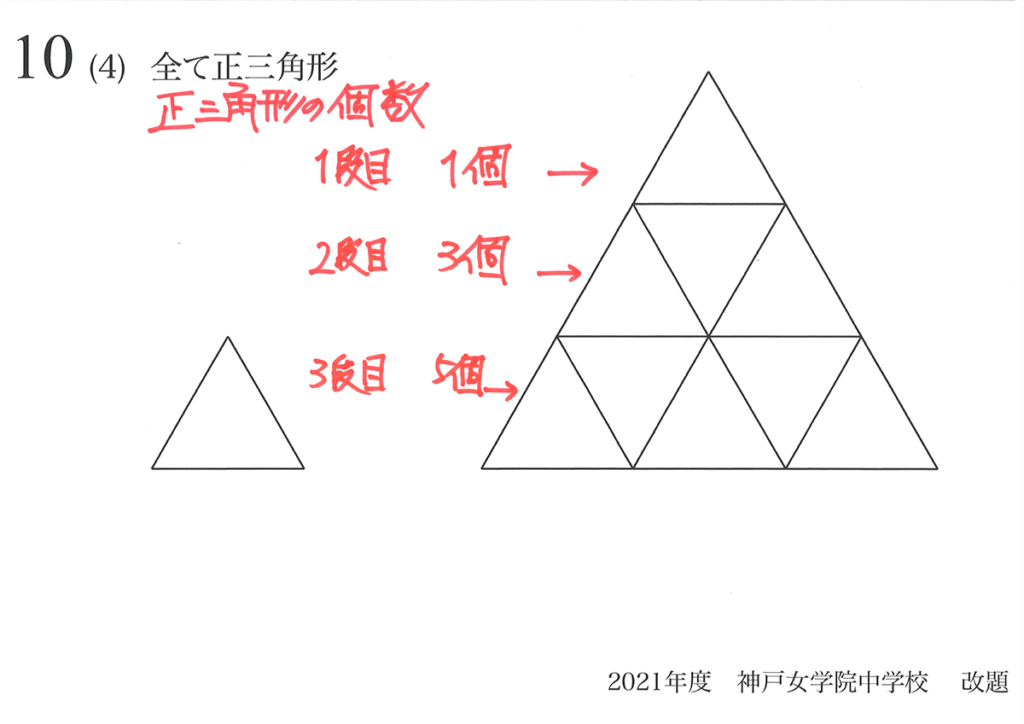
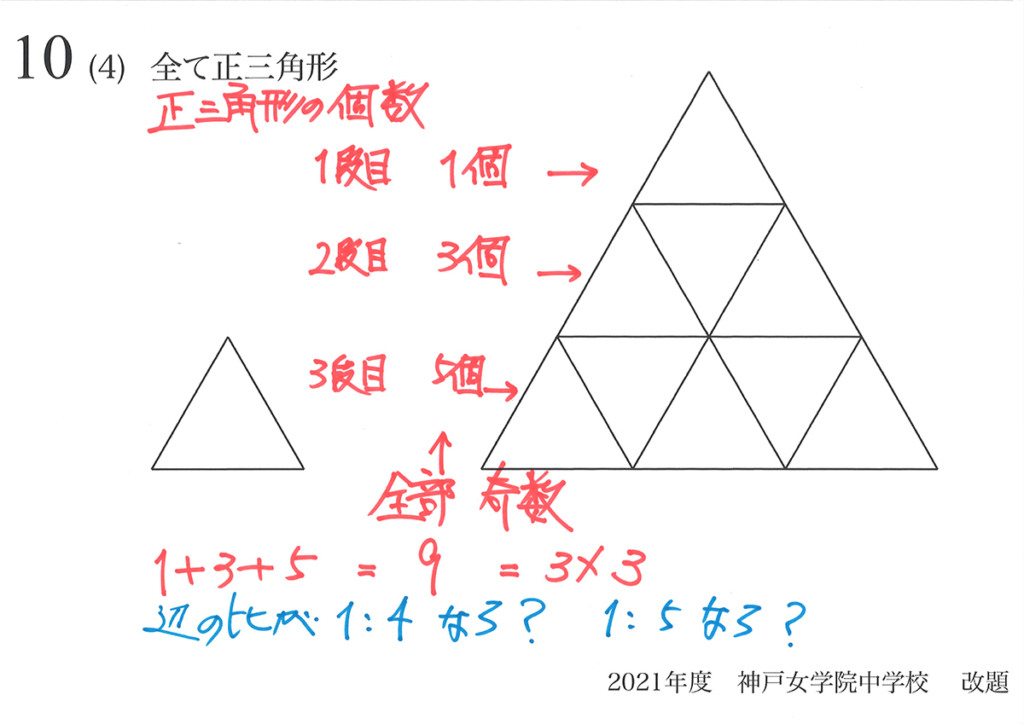
小さな正三角形で分割してみた、上の段から順に個数を数えてみましょう。
図形は中学以降は幾何（きか）と呼びます。
対して、「未知数を置いて解く」などの考え方は代数（だいすう）と呼びます。
「きか」と
「だいすう」？
中学になると、
難しそうな言葉になるのね。
今回は、「図形的な幾何」と「分析的な代数」の接点の話です。
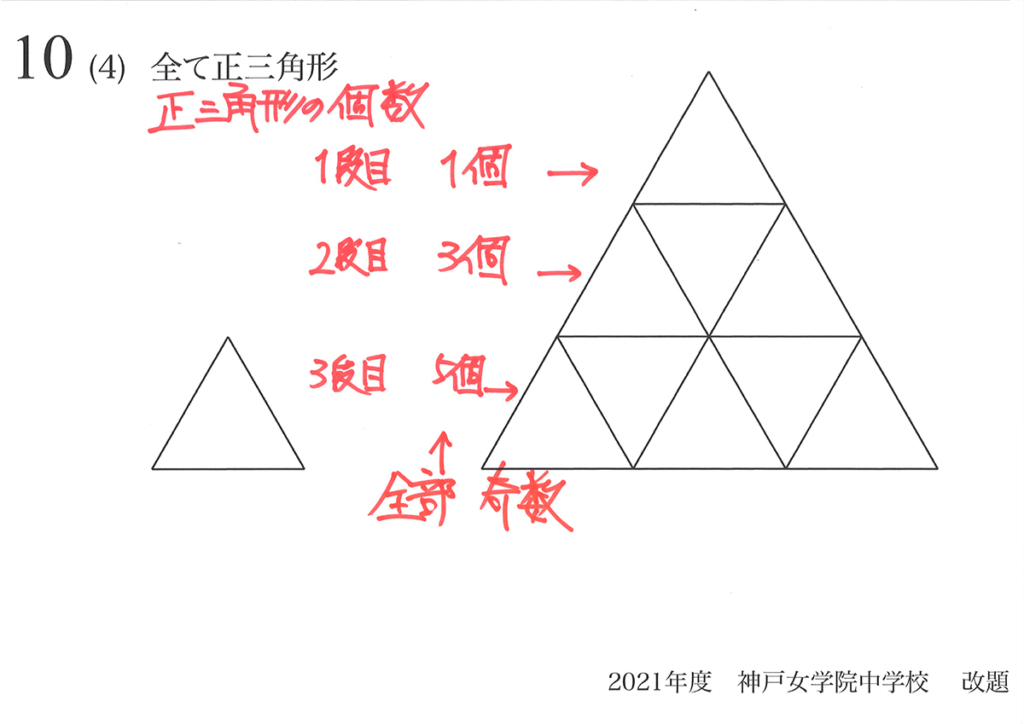
1段目から順に1,3,5個と奇数が、順番に並びました。
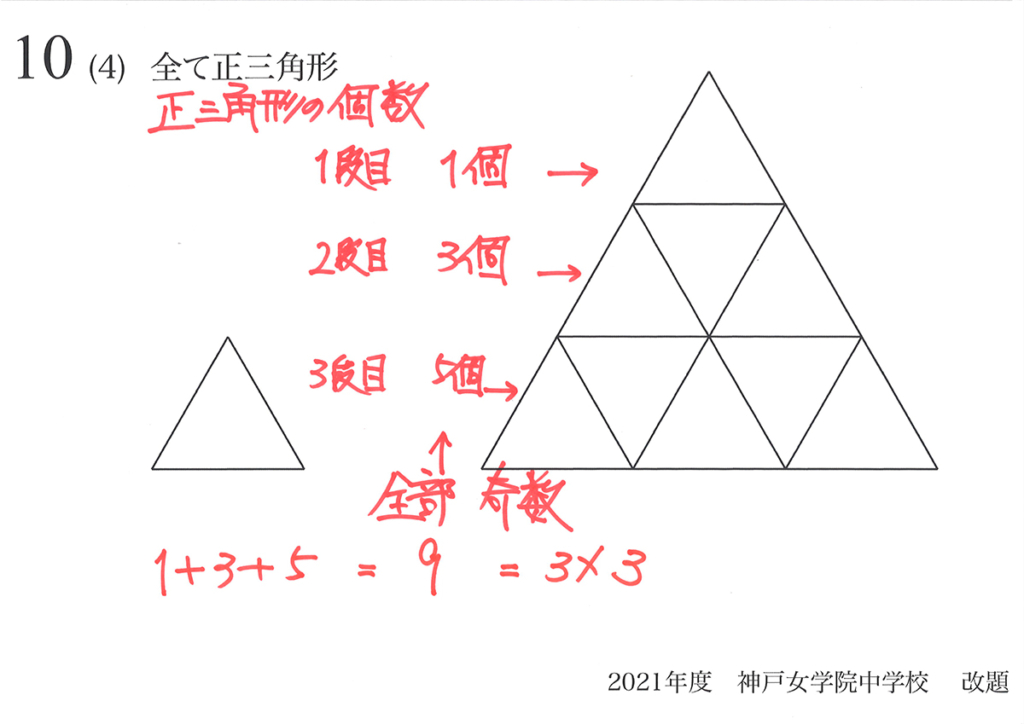
上の段から足してみましょう。
1+3+5と奇数を順に足してゆくと、9になります。
そして、この9は相似比で考えた「3×3」です。
不思議
だね・・・・・
合計すると相似比に
なるのは分かるけど・・・
上から「1,3,5と奇数が並ぶところ」が不思議です。
「横道にそれる」を楽しんで図形を得意に
中学受験で、累乗の問題が出題されることがあります。
「累乗」は中学の範囲ですが、一部の試験で見受けられます。
例えば、3×3は「3の自乗（じじょう）」あるいは「3の2乗（にじょう）」と言います。
と言うことは、相似比が4とかだと
同じようになるの？
相似比「1 : 4」や「1 : 5」の時も描いてみましょう。
自分で
描いてみる！
方眼紙使えば
楽に描けるね！
相似比「1 : 4」の時は、上と同様に考えて、
「1 + 3 + 5 + 7 = 16」となります。
また、
奇数だけが並んで、4の自乗になったね！
この話は、今回の問題を解くことには無関係です。
算数って、
楽しいかも！
受験生は、まだ時間に余裕があります。
たくさん
問題やらなきゃ！
と焦る気持ちも分かります。
今は、このように算数の楽しさ、不思議なところも感じてみて下さい。
解けないと悔しい算数ですが、色々と考えてみるのは楽しいですね。
楽しくなって、好きになると、もっと出来るようになります。
本当？
楽しくなると、「自分から、どんどんやる」から、ますます出来るようになるのです。
そうかも。
楽しむ気持ちを持ってみましょう。
