公式を暗記ではなく理解して学力アップ〜相似形の面積比・図形のイメージ・方眼紙と図形・問題10(4)ポイント〜｜面積の最小2・算数・過去問・中学受験

前回は「動く点を苦手に思わないコツ・ポイント〜動点P・移動する図形・点が動くのを描いてイメージ・動画のイメージ・動画は静止画の連続・問題10(4)〜」の話でした。

問題10(4)（再掲載）

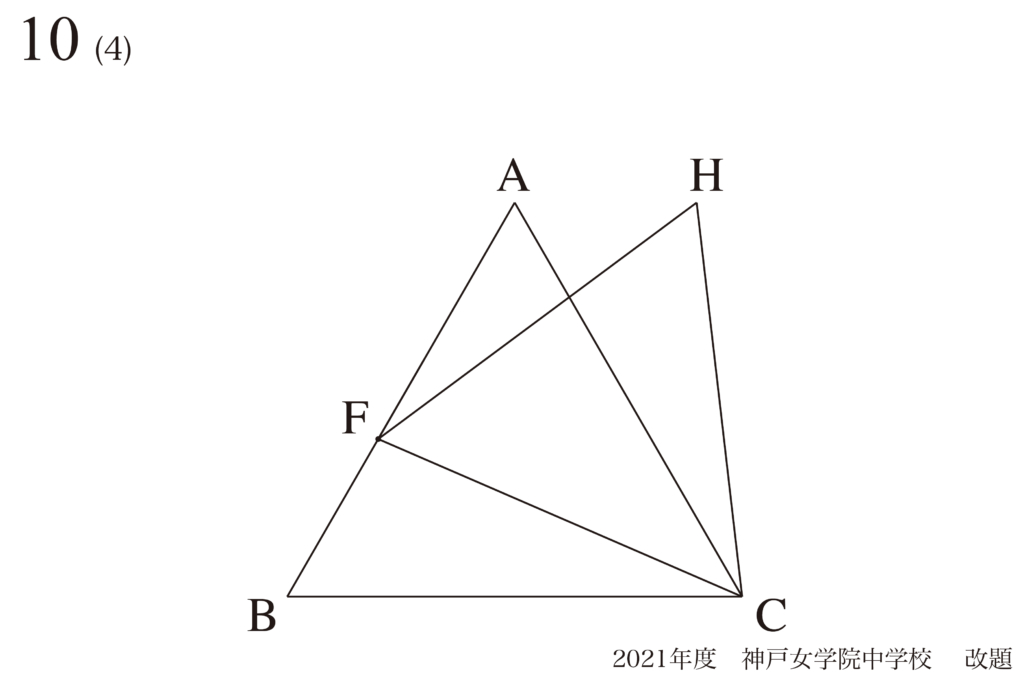
相似形の面積比：辺の比と面積比

今回は、相似形の面積比を考えます。

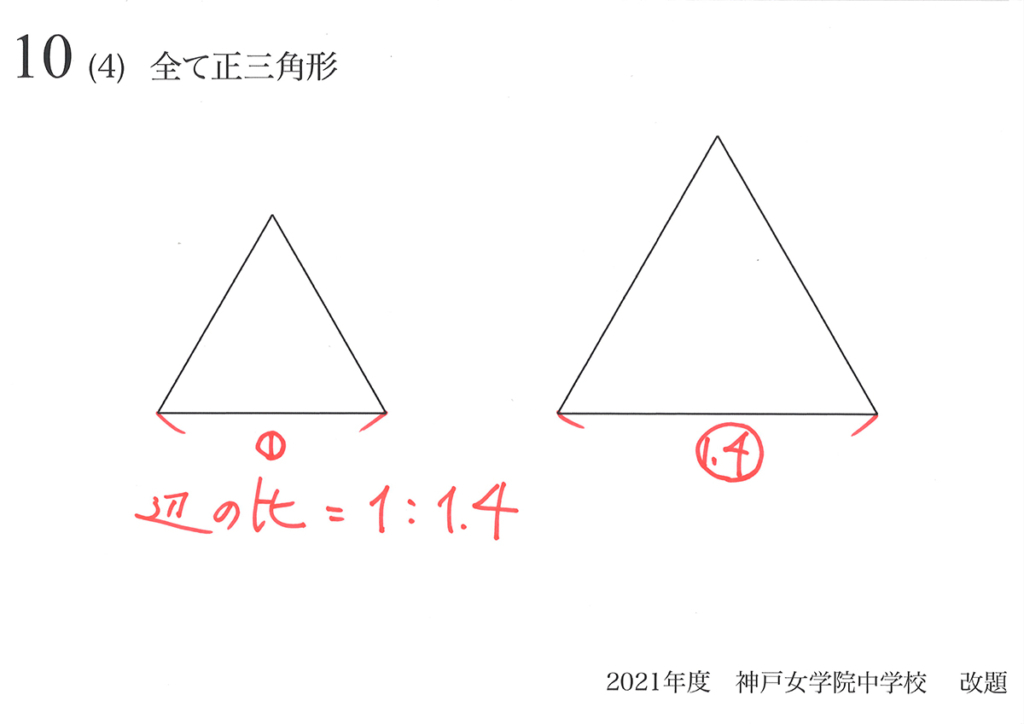
正三角形は、お互い全て相似形です。

下の図のように辺の比が 1:1.4 の時、面積比はどうなるか考えてみましょう。

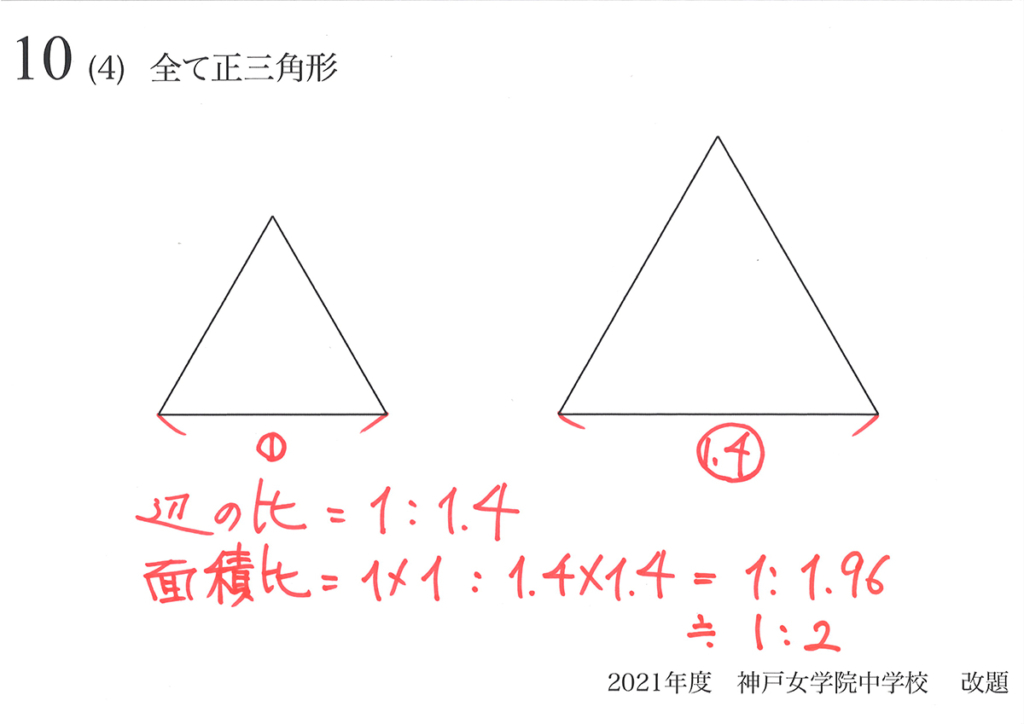
計算すると、1:1.96になります。

1 : 1.96 は「約 1 : 2」 です。

「辺の長さは、40%しか違わないのに、面積は約2倍になる」ことを実感しましょう。

「当たり前のこと」に感じるかもしれませんが、こういうことを「しっかり実感すること」は大事です。

公式を暗記ではなく理解して学力アップ

先ほどの、「相似形の面積比は(辺の比)x(辺の比)」を、きちんと説明できますか。

これは正三角形に限らず、全ての相似形（平面）で、成立します。

きちんと説明できるか、考えてみましょう。

これに限らず、「公式」は「説明できるように理解」しましょう。

ただ「公式」として覚えていると、応用力が育ちません。

「まる覚えしているだけ」だと、

このように「どのように公式を使うか？」が分からない場合があります。

公式を知っていることよりも、「公式を使う・運用すること」が大事です。

そして、「公式をきちんと理解していれば、応用力が育つ」ようになります。

そして、「公式を忘れてしまっても、理解しているから、すぐ自分でつくれる」くらいが望ましいです。

この相似比が(4)を解く鍵になります。

ぜひ、「公式の理由」を考えてみましょう。

図形のイメージ：方眼紙と図形

未就学児〜小学校低学年の頃は、大勢の方が「方眼紙で工作」をします。

小学校年長になると、少し縁遠くなる方眼紙。

図形問題をイメージするときは、方眼紙のイメージを思い出しましょう。

1cm（10mm）ごとに縦横に線が引いてある便利な方眼紙。

「寸法を測る必要がない」ので、工作をする際はとても便利です。

相似形の面積比は「計算して理解する」ことも大事ですが、イメージしましょう。

「相似形が大きくなる」は「図形を作る（構成する）元の方眼紙が縦横に伸びる」感じです。

図形問題を解く際に大事なのは、面積や比を求める論理性とイメージです。

次回は相似形の面積比に関して、考える話をご紹介します。

次回は下記リンクです。