前回は「図形問題を根気よく解くコツ・ポイント〜根気よく考える姿勢・5点並んだ辺の比・連比を考える・問題10(3)解法B〜」の話でした。
問題10 (4)
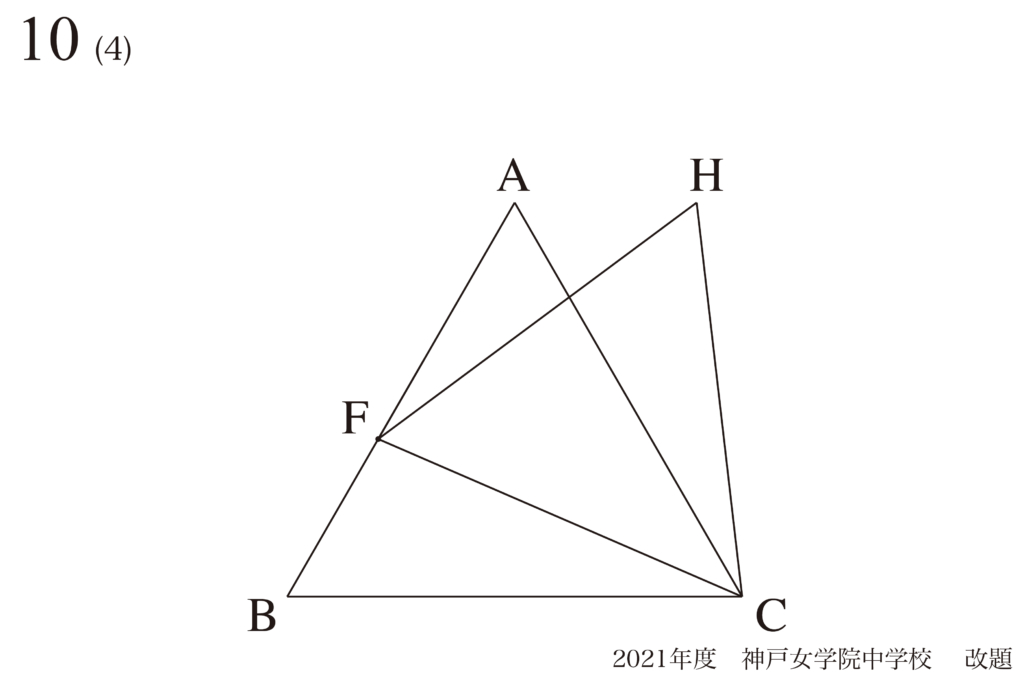
点が動くのを描いてイメージ
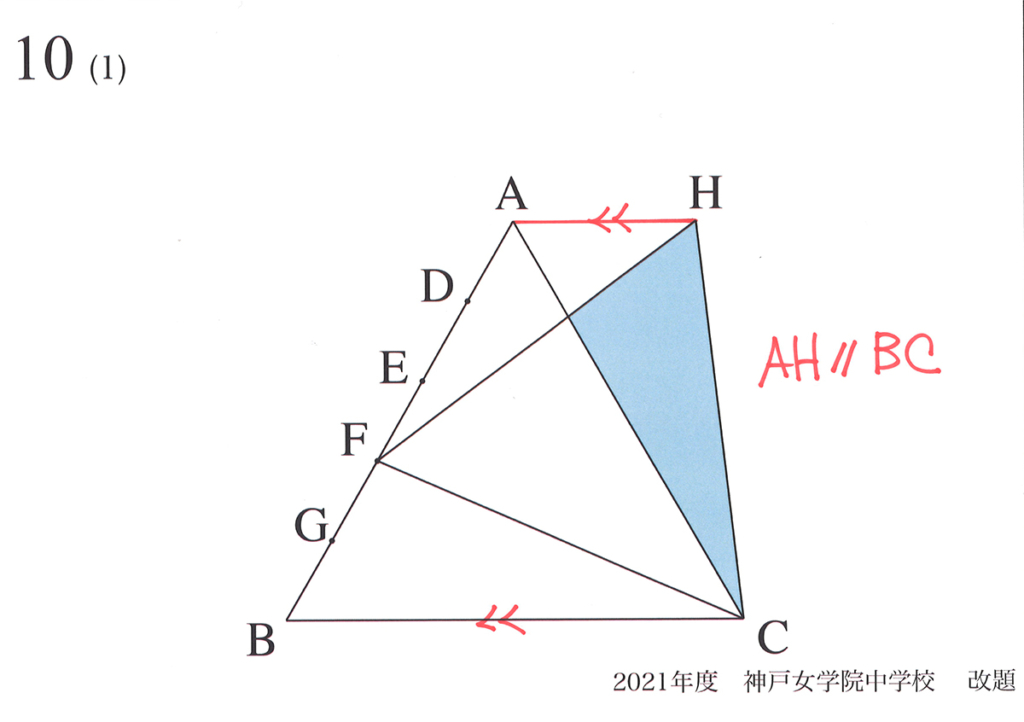
今回は、応用力を試される(4)です。
(1)〜(3)では「ABを5等分にする点D,E,F,G」が登場しました。
今回は点Fが「AB上、どこでも良い」です。
動点になるので、動点Pなど名前を変えても良いです。
男子小学生動く点の問題って、
難しいんだよね・・・
女子小学生動く点を追っていると、
混乱しちゃって・・・
今まで色々と考えて、性質が良く分かっている点F。
「点Fが、点PとなってAB上を動く」と考えれば「点F=点P」です。
男子小学生それは
そうだけど・・・
男子小学生名前が変わっただけだから、
なかなか分からないけど・・・
動く点を苦手に思わないコツ・ポイント：動点P・移動する図形
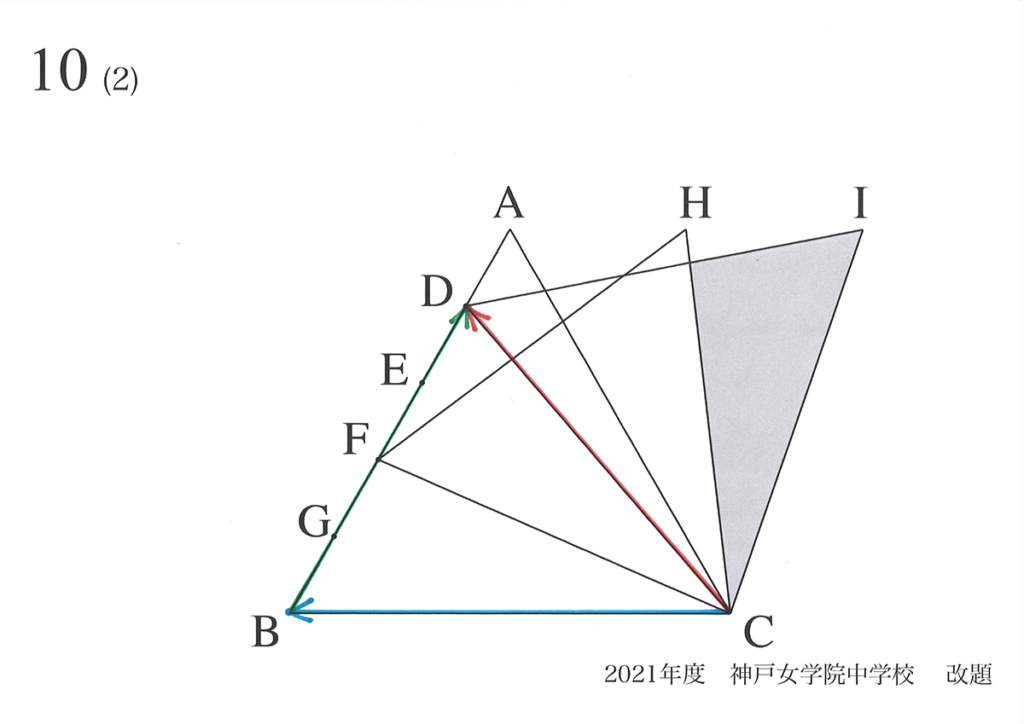
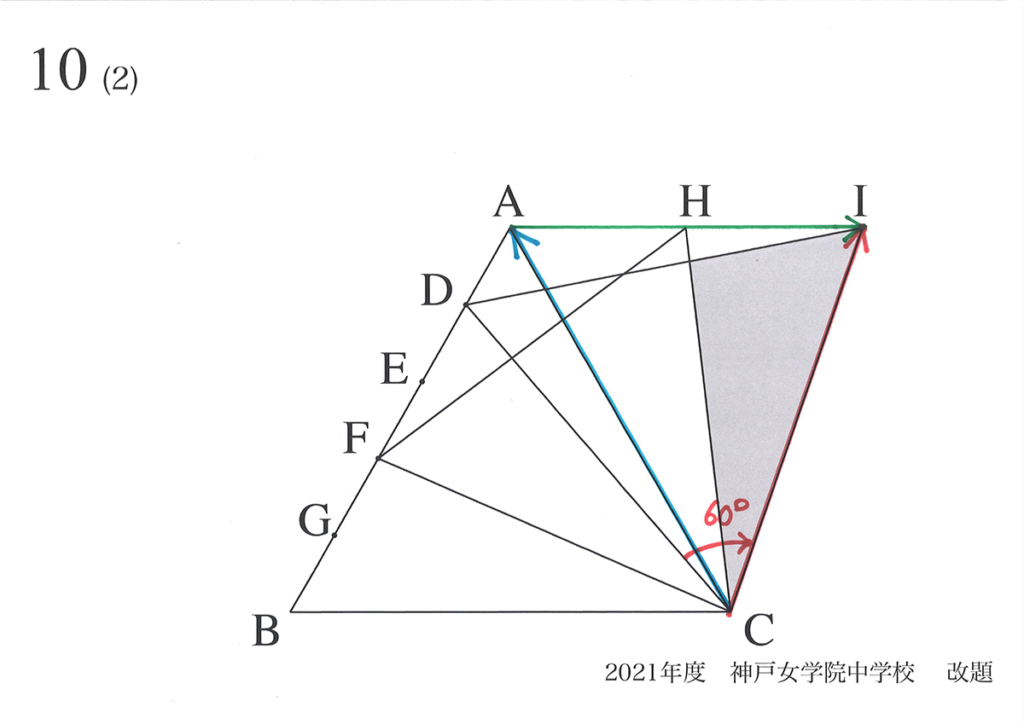
(1)(2)で△HFC、△IDCの面積を求めました。
これらの図形の面積を求める話を、上記リンクでご紹介しています。
男子小学生ここまでは、
ちょっと計算が大変なところがあるけど分かった！
女子小学生でも、
動く点になると、話が全然違うよね・・・
男子小学生そう・・・
(1)から(3)までは、「ABの五等分の点」だったじゃん・・・
男子小学生それが「動く点」になると、
「AB上のどこでも良い」し、さらに「動く」から・・・
女子小学生ちょっと
難しいね・・・
辺AB上の点が「ABの五等分の点」の時は、「点の位置が限定」されます。
そして、「動く点」は「点の位置が無限にあって、移動する」ところが難しいところです。
女子小学生そう・・・
考えるのが「無限にある」のは困る・・・
ここが、「動く点P」の問題の難しいところで、「点を止める・固定する」考え方があります。
男子小学生そう！
「動く点は止める」が鉄則って習った！
男子小学生でもさ、なぜ「動いている」のに
勝手に「止める」ことが良いの？
女子小学生「動いているから困る」のであって、
「止めるが鉄則」と言っても、良く分からなくなる・・・
高校数学などでも「動く点が二点・動く量（変数）が二つ」の時は「一方を固定」が「鉄則」です。
この「固定する・止める」は大事な考え方ですが、しっくりこない点があります。
「動くから難しい」のに、
塾講師動点は
止めれば良い！
このように言われても、理解するのは難しいと感じる方が多いでしょう。
動画のイメージ：動画は静止画の連続
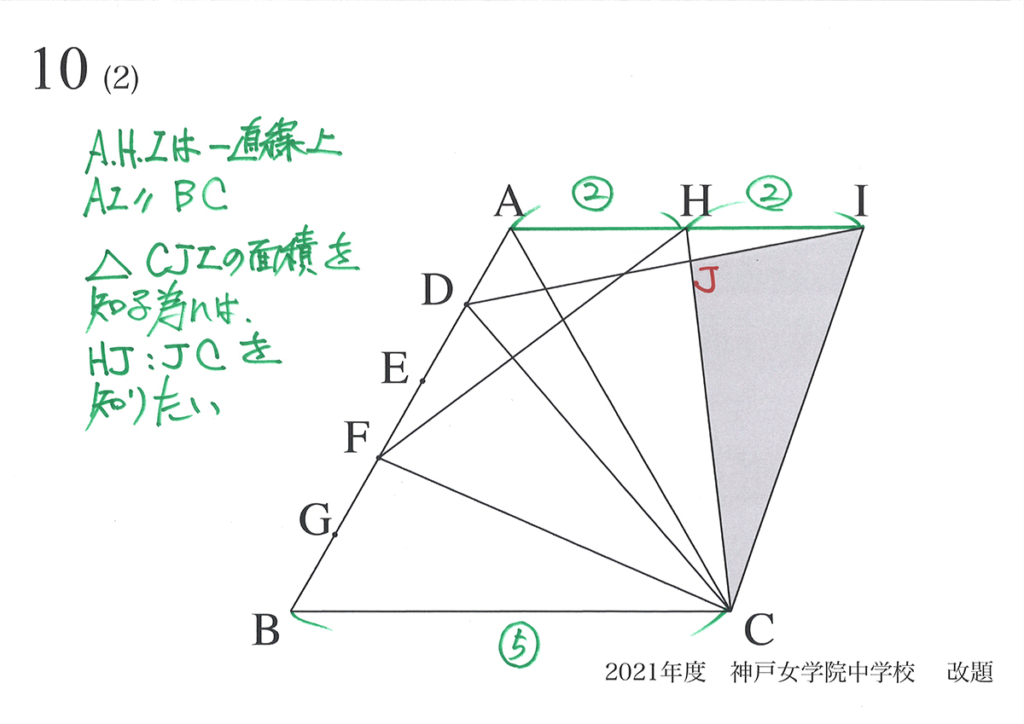
今回の問題では「ABの五等分の点」を先に考えたことがポイントです。
「動く点P」の位置は「位置が無限にある」のですが、そのうち「代表的な点=五等分の点」と考えましょう。
男子小学生「代表的な点」かあ・・・
確かに動く点は、G→F→E→Dと動くね！
女子小学生このB→G→F→E→D→Aと
点Pが移動するときの、一部は分かっているんだね！
動く点は「連続的に移動する」から難しいと感じます。
ここで、動く点が「連続的」ではなく「飛び飛びの位置を移動する」と考えてみましょう。
男子小学生連続的に移動するのではなく、
B→G→F→E→D→Aと移動することを、まず考えるのかな？
そして、「移動する状況」を描いてみましょう。
これは、動画の原理と同じと考えてみましょう。
・1秒間に24枚の写真が連続的に映し出される（枚数は違う場合があります）
・1枚あたり1/24秒=約0.04秒なので、本当は「静止」しているのに、連続的に「動画」に見える
この動画のように「動く点をイメージ」してみましょう。
B→G→F→E→D→Aを「動く」際には、どこかのタイミングで点B、G、F、E、D、Aにいる時があります。
女子小学生確かに
そうだね！
そこで、「動く点がB、G、F、E、D、Aにいる時」を考えると、「大体の様子が分かる」のです。
・連続的に、無限の点を移動するから難しい「動く点」
・代表的な点をいくつか選んで、具体的に描いてイメージする
・代表的、いくつかの点での状況（静止画）がたくさん並んで「動く点=動画」になるイメージ
女子小学生いつも見ている動画って、
実は「動いていない」のね！
男子小学生短い時間で写真をたくさん見るから、
「動くように」見えるだけなんだね。
女子小学生そういえば、「パラパラ漫画」って見たけど、
動画みたいに見えた！
「動く点」を難しく考えないで、「具体的な点でイメージする」ようにしましょう。
中学以上では「証明してください」になります。
小学生ですから「証明」ではなく「説明」としました。
「説明」には厳密な数学的論理性は不要ですが、「大事なポイント」は説明する必要があります。
いくつか考え方ありますが、考えてみましょう。
次回は下記リンクです。
