前回は「相似三角形をつくるコツ〜「根幹となる図形」の性質・平行な線を補助線に・根気よく相似形をつくる・少しずつ解明・問題10(3)解法A〜」でした。
問題10（再掲載）
図形の面積のコツ・ポイント：「どの辺の比を求めるか」を明確に
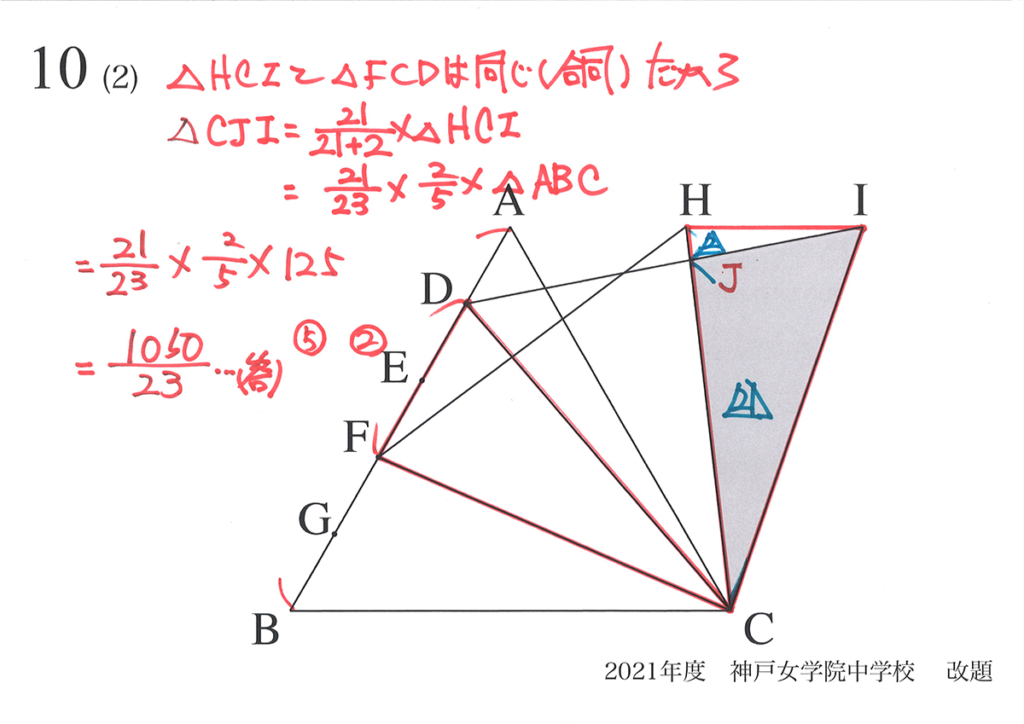
今回は(3)を、(2)で考えた面積から求める解法Bを考えてみます。
(2)で面積を求めた状況を振り返りましょう。
どの部分の比が分かれば、黄色の部分の面積が求まるでしょうか。
女子小学生ええと・・・
HJ : JCの比が分かっているから・・・
女子小学生この直線と交差する部分の
辺の比が分かれば解けそう・・・
図形問題は、「答えを求めるためには何が分かれば良いか」を常に考えましょう。
・「問題を解くには、Aが分かれば良い」という「Aを考える」姿勢
・「Aを知るためには、どのようなことが分かればよいか」を考える
・少しずつ、着実に答えに近づいてゆく姿勢
そして、「面積を求める際には、辺の比が二つ分かれば分かる」ことが多いです。
「どのような辺の比が分かれば、面積が求めるか」を考えて、しっかりと目標をはっきりしましょう。
・近く又は隣接する「面積が分かる図形=基準となる図形」を基準に考える
・「面積が分かる図形=基準となる図形」と求める図形に関わる辺の比を求める（大抵二つ）
・辺の比は「一つは分かっている」ことが多く、もう一方は「分かっている比と交差する位置」
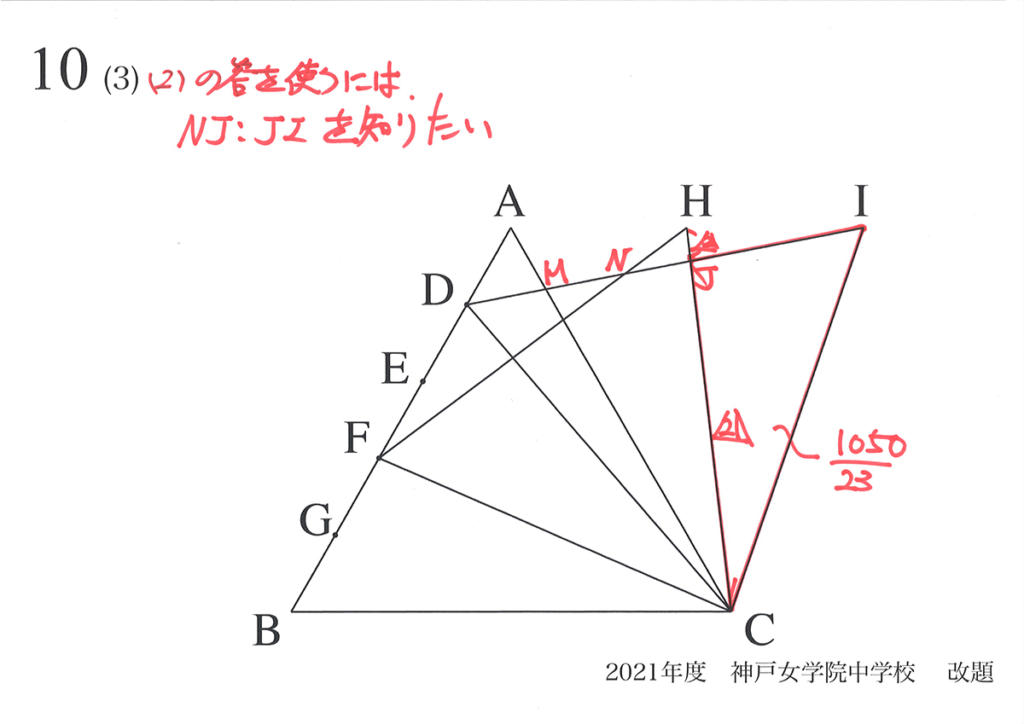
黄色の部分の面積を利用するためには、上のNJ : JIを知りたいです。
女子小学生確かに、この比が分かれば、
黄色の部分の面積が分かるね！
すると、(2)の面積からHJ :JC=2 :21とNJ : JIで黄色の部分の面積が出ます。
上手い相似形が見つからない時：特徴的な方向を最重視
男子小学生NJ : JIの比が分かれば、
解けるのは分かったけど・・・
男子小学生NJ : JIの比って
分かるの？
女子小学生パッと
相似形が見えてこないね・・・
NJ : JIを一気に求める相似形は、なかなか見えません。
自分でも色々と「ある辺に平行な線」を引いて、相似形を描いてみましょう。
この問題では、正三角形ABCが大事です。
正三角形ABCの「辺AB上に点を取って、新たに正三角形をつくっている」からです。
つまり、正三角形ABCは「この問題の根幹となる図形」と言っても良いでしょう。
・正三角形・正方形など基本的な図形が「根幹となる図形」の時は、常にその図形に注目
・「根幹となる図形」のある辺と「平行な辺」があるときは、その辺に注目
この問題は「辺BCと平行な直線」が大事です。
上の図形では「水平・真横の直線」です。
図形問題を考えるときは、「特徴的な方向を最重視する」ことが大事です。
・「根幹となる図形」の最も大事な辺を考える
・その辺が水平・垂直、あるいはそれらと60度など分かりやすい角度の時は、その方向を最重視
なかなか「辺の比が分からない」時は、「いくつかの相似形による辺の比」を考えましょう。
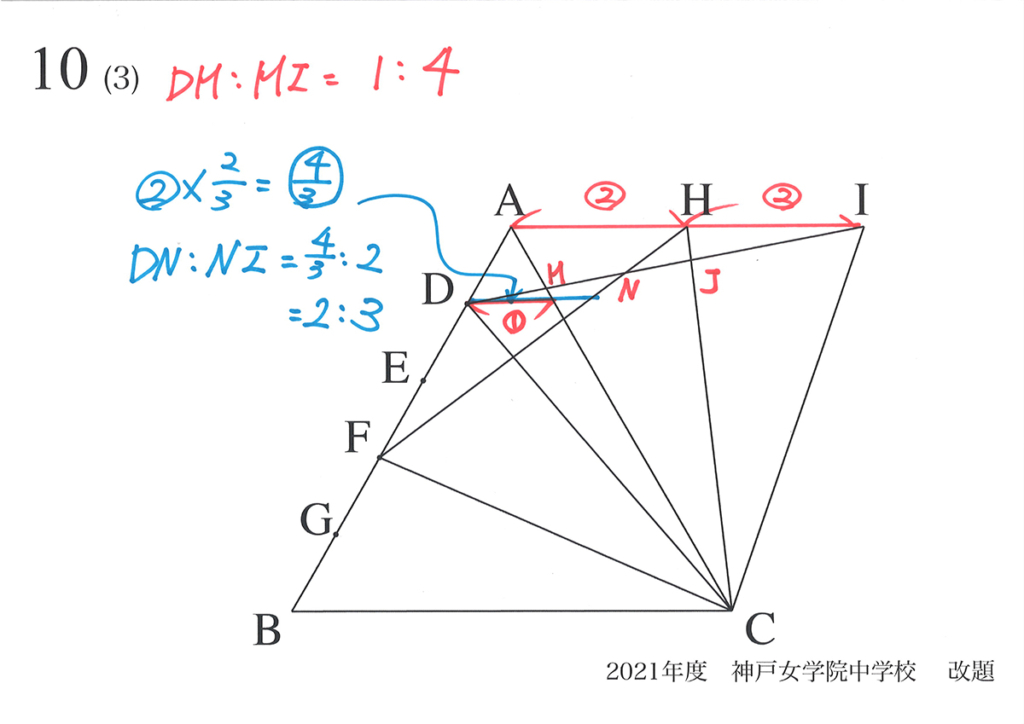
上の図で、DM :MI=1 : 4 はすぐに分かります。
女子小学生確かに、
これは分かるかも！
AHと水色の線が平行なので、DNは△FAHの相似形から計算できます。
女子小学生この問題では、
水平方向の補助線がキーポイントだね！
そして、DN :NI も計算できます。
このように、「いくつか相似形を考えて」NJ : JIを求めましょう。
・解答に至らない「無駄なこと」が大事
・「遠回り」や「無駄」を経験すると、試験で「何が大事か」の感覚が磨かれる
この問題の鍵は「水平方向の補助線」です。
「水平方向の補助線を引けば、辺の比がもとまり、面積がもとまる」はずです。
色々と補助線を引いて、考えてみましょう。
次回に解法をご紹介するので、手を動かして考えてみましょう。
次回は下記リンクです。
