前回は「算数実践44〜問題 10(3)(図形)解き方A・辺の比のコツ〜」の話でした。
問題10(再掲載)

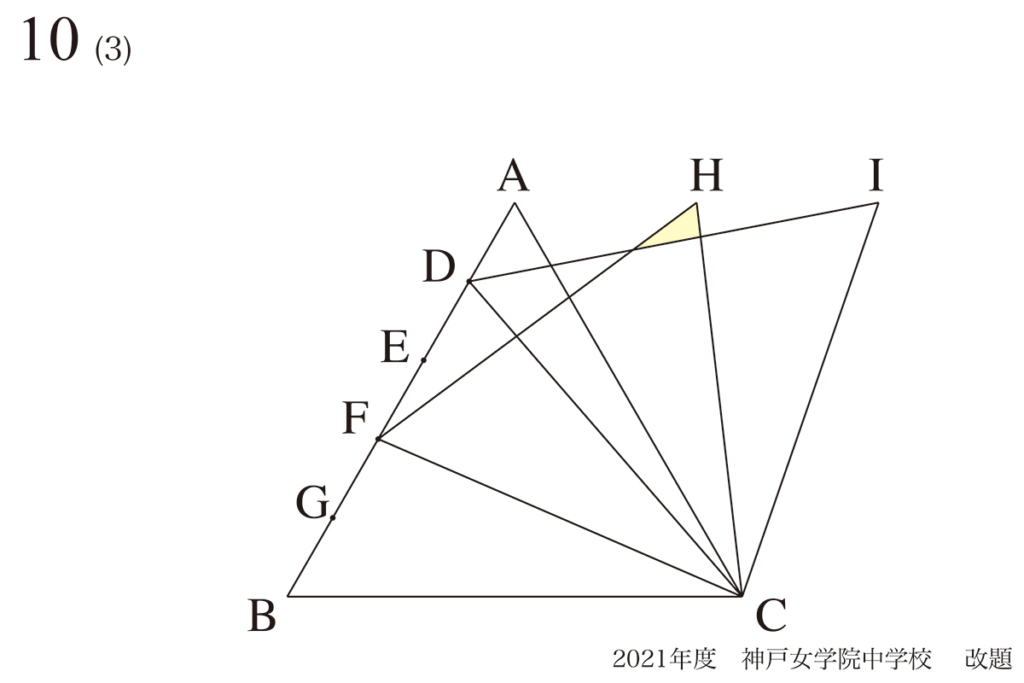
相似三角形をつくるコツ:「根幹となる図形」の性質
(1)で求めた面積から、黄色い部分の面積を求めてみましょう。
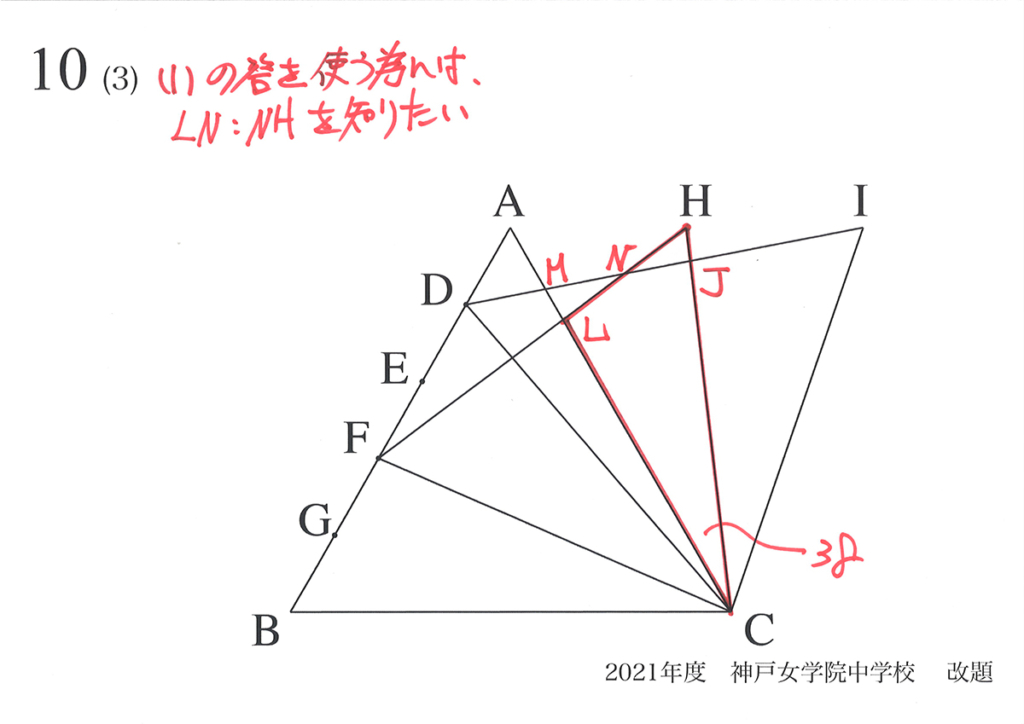
LN : NHを求めてみましょう。
直感的にわかるかも知れませんが、きちんと求めてみましょう。
LN : NHを求めるためには、これらの辺が関係する相似形を見つけたいです。
 男子小学生
男子小学生相似形が
見つからないけど・・・
ところが、相似形がなかなか見つかりません。
・平行な直線があると、その周辺に相似形がある
・相似形が見つからないときは、自分で相似形をつくる
この問題では、正三角形ABCが大事です。
正三角形ABCの「辺AB上に点を取って、新たに正三角形をつくっている」からです。
つまり、正三角形ABCは「この問題の根幹となる図形」と言っても良いでしょう。
・正三角形・正方形など基本的な図形が「根幹となる図形」の時は、常にその図形に注目
・「根幹となる図形」のある辺と「平行な辺」があるときは、その辺に注目
今回は、「辺BCと辺AH、AIが平行」であることが大事なポイントです。
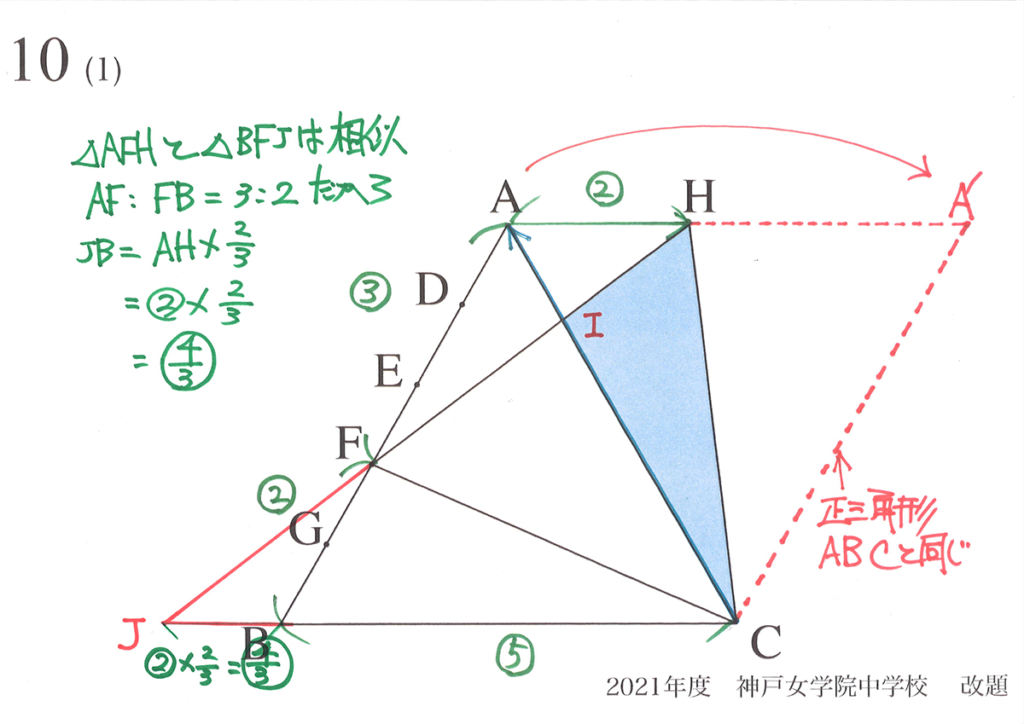

辺AB上のどの点を取って、正三角形HFCなどを新たに作成しても、必ずAHとBCは平行です。
そこで、「AH,HIと平行な線を補助線にすれば、相似形が見えてくるはず」です。
平行な線を補助線に
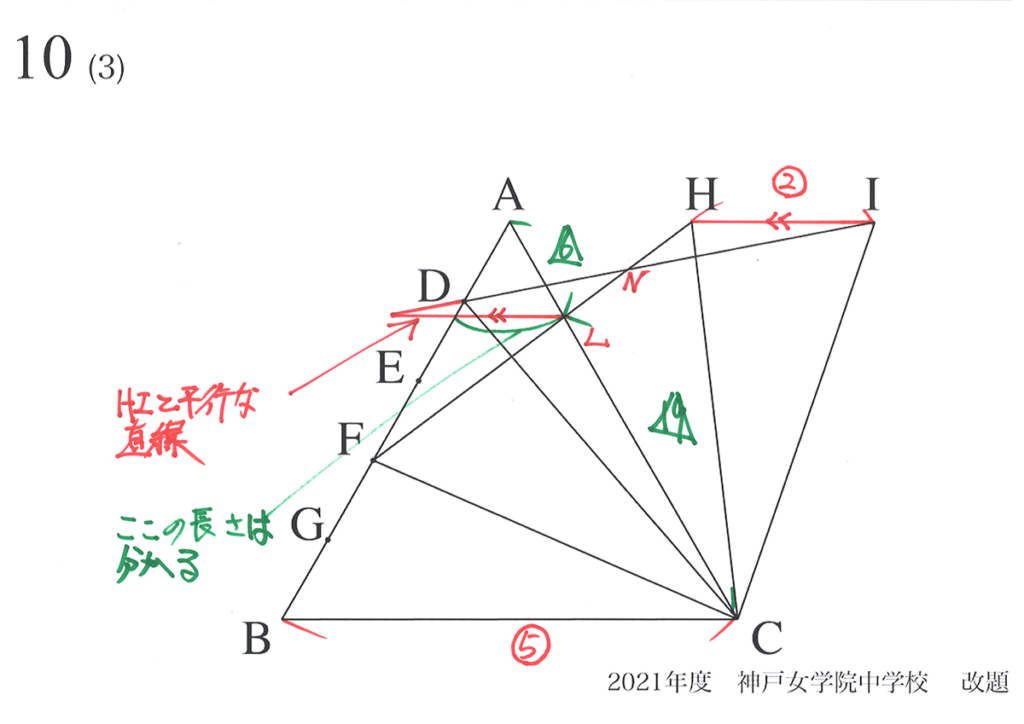

HIの長さがわかっているので、LからHIに平行な直線を引いて、相似三角形を作りましょう。



新しい直線が2本、
そして新しい交点が出てきた・・・



分からないことが
多くて、難しそう・・・
上の図のように「分からないこと」がたくさん登場してきても、驚かないようにしましょう。
「分かっていること」も多く、大事な辺と平行な直線を補助線にしたので、相似形があるはずです。
「相似形をつくる・見つけることが出来れば、問題は解けるはず」と考えることも大事です。
(1)からAL : LC=6 :19 と分かっているので、緑色の部分の長さは分かりそうです。
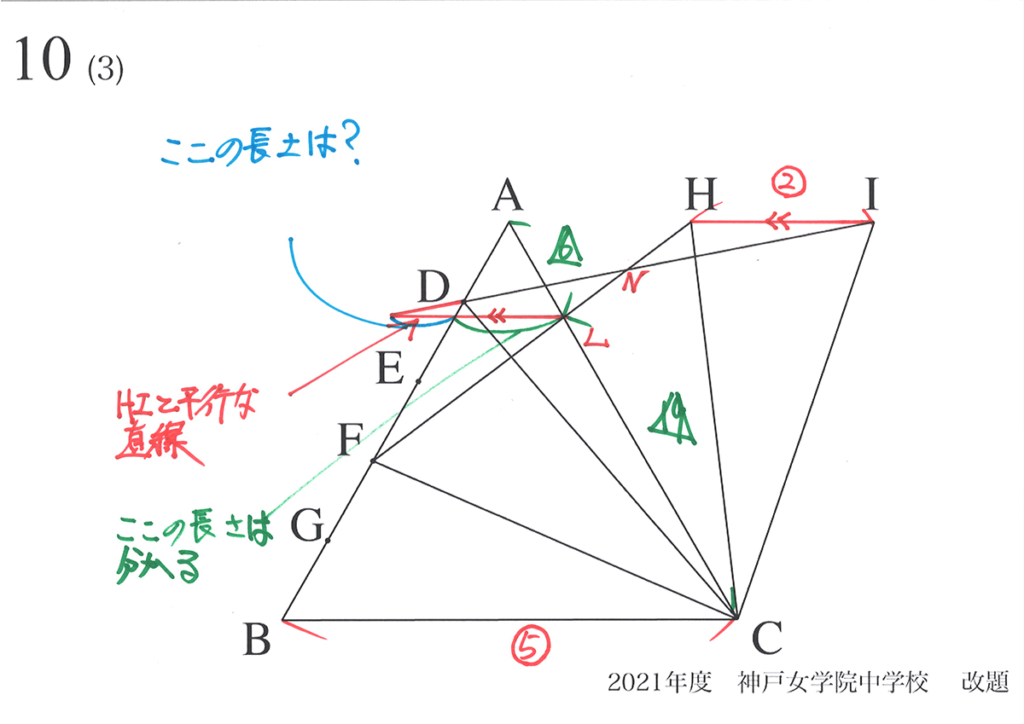

それでは三角形が閉じていないので、LN : NHを知るには、下図の水色の部分の長さが必要です。



あれ?
ダメじゃん・・・
ここで、諦めないようにしましょう。
図形問題は色々な考え方がありますが、少し遠回りしても、自分で考えれば解けることが多いです。
そのためには、「自分で相似図形を作る」姿勢が大事です。
根気よく相似形をつくる:少しずつ解明
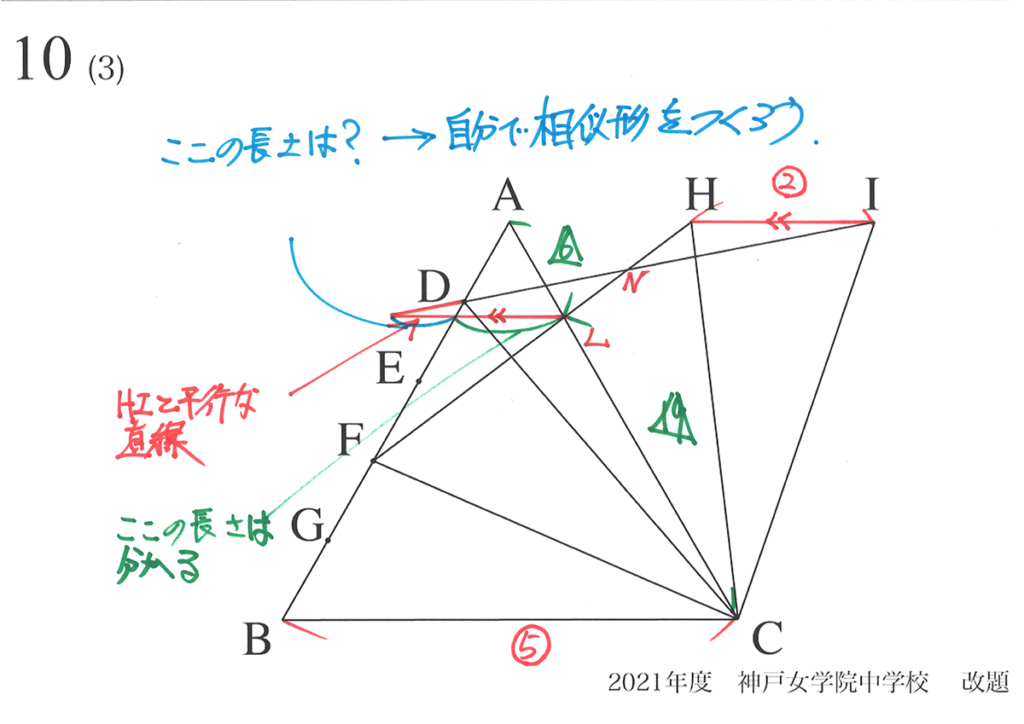

こういう時は、自分で「新しく図形を作ってでも、なんとか求めよう!」と考えましょう。
水色の部分の長さを求めるには、(2)と同様に図形の外に飛び出してみましょう。
先に進む前に、少し考えて下さい。
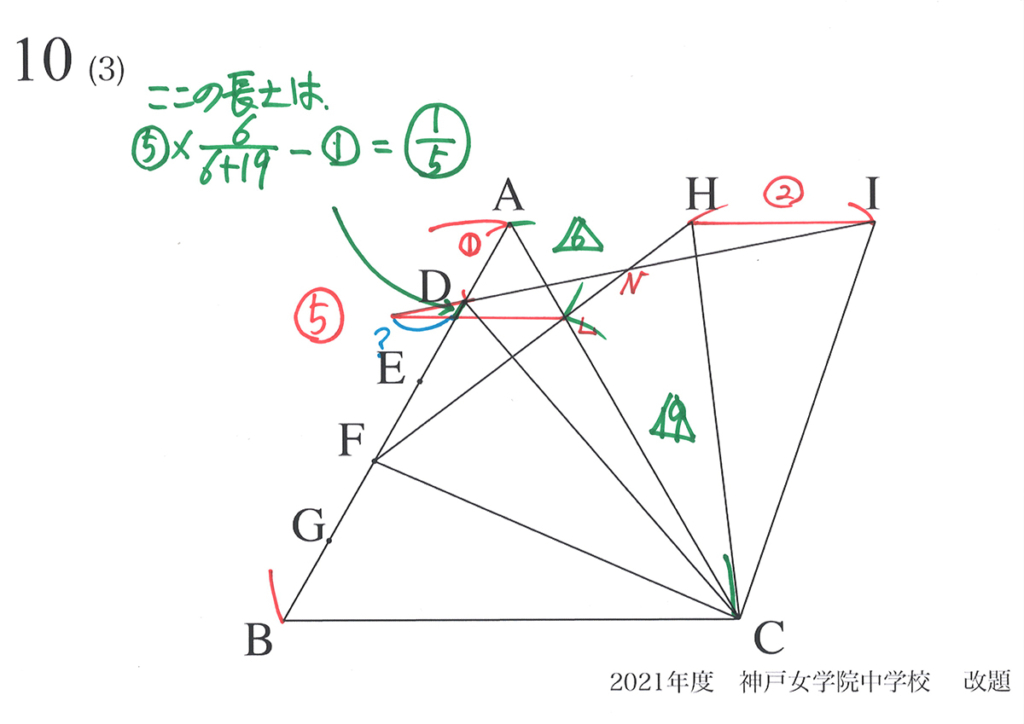

(2)と同様に外に図形を作りますが、必要な長さを求めましょう。
・平行な直線のうち、一つまたは二つの直線を延長する
・平行ではない直線を延長して、新たな交点を作ると相似形が出てくる
思い切り外に出て、相似三角形を作ってみましょう。

そして、必要な長さを分割して計算し、足してみましょう。
・「問題を解くには、Aが分かれば良い」という「Aを考える」姿勢
・「Aを知るためには、どのようなことが分かればよいか」を考える
・少しずつ、着実に答えに近づいてゆく姿勢
図形問題で「ある長さを求める」時は、少しずつ「何を知りたいか」を考えることが大事です。
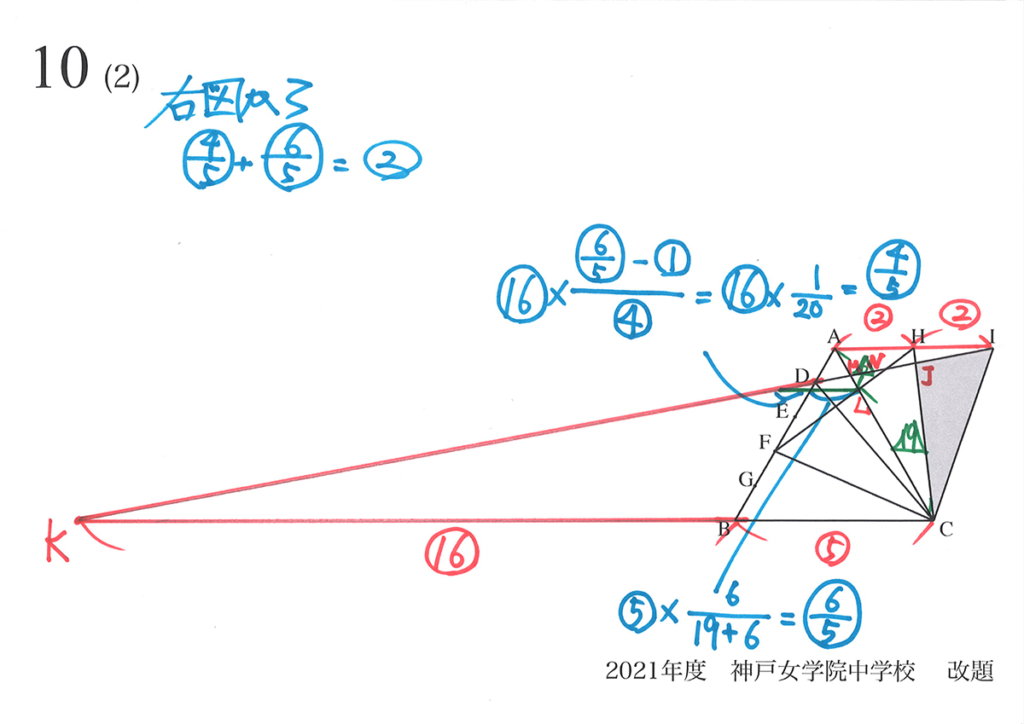
水色の部分の長さは、△DKBとその内部の小さな三角形が相似形です。
・平行な線、相似形を探す・つくる
・相似比となる「対応する辺」の長さを計算
・「対応する辺の長さ」が分かりにくい時は、辺を分割して考える
そこで、上図の通り長さがもとまります。
整理すると、実は考えていた相似形の辺の長さが同じなので、LN=NHと分かります。
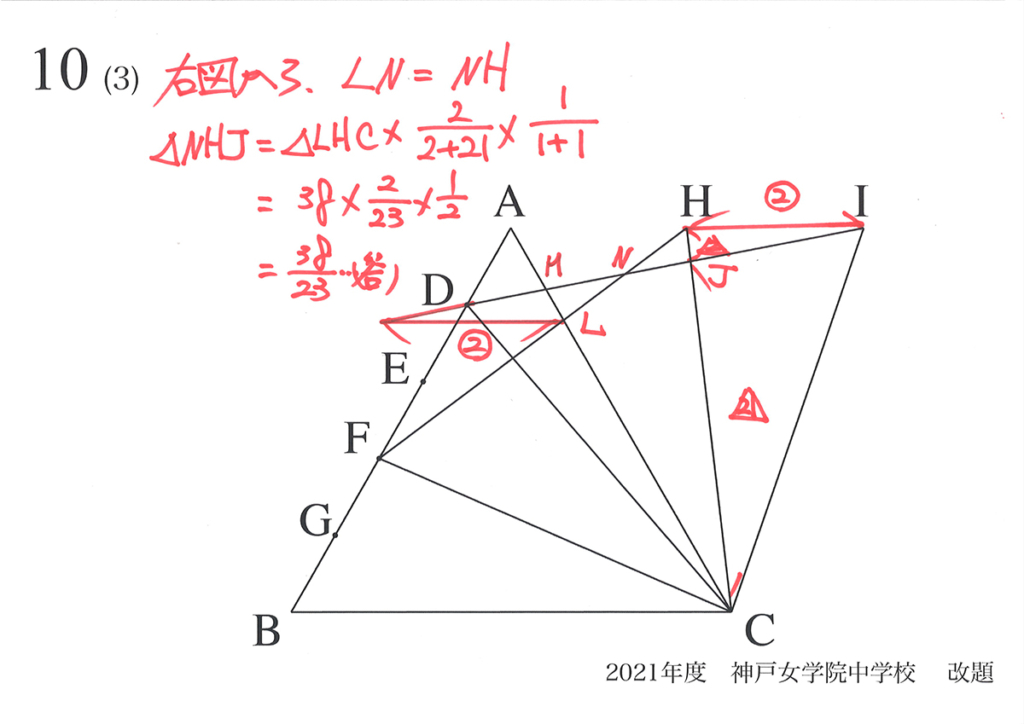

ここまで来れば、黄色い部分△NHJの面積は計算できます。
では、今度は(2)の結果から、面積を求めてみましょう。
同様に手を動かして考えてみましょう。
・解答に至らない「無駄なこと」が大事
・「遠回り」や「無駄」を経験すると、試験で「何が大事か」の感覚が磨かれる
次回は下記リンクです。


