前回は「図形の面積を考えるコツ・ポイント〜正三角形・前の問題をヒントに後ろの問題を考える姿勢・どの辺の比が分かれば解けるか・問題10(3)解法〜」の話でした。
問題 10（再掲載）
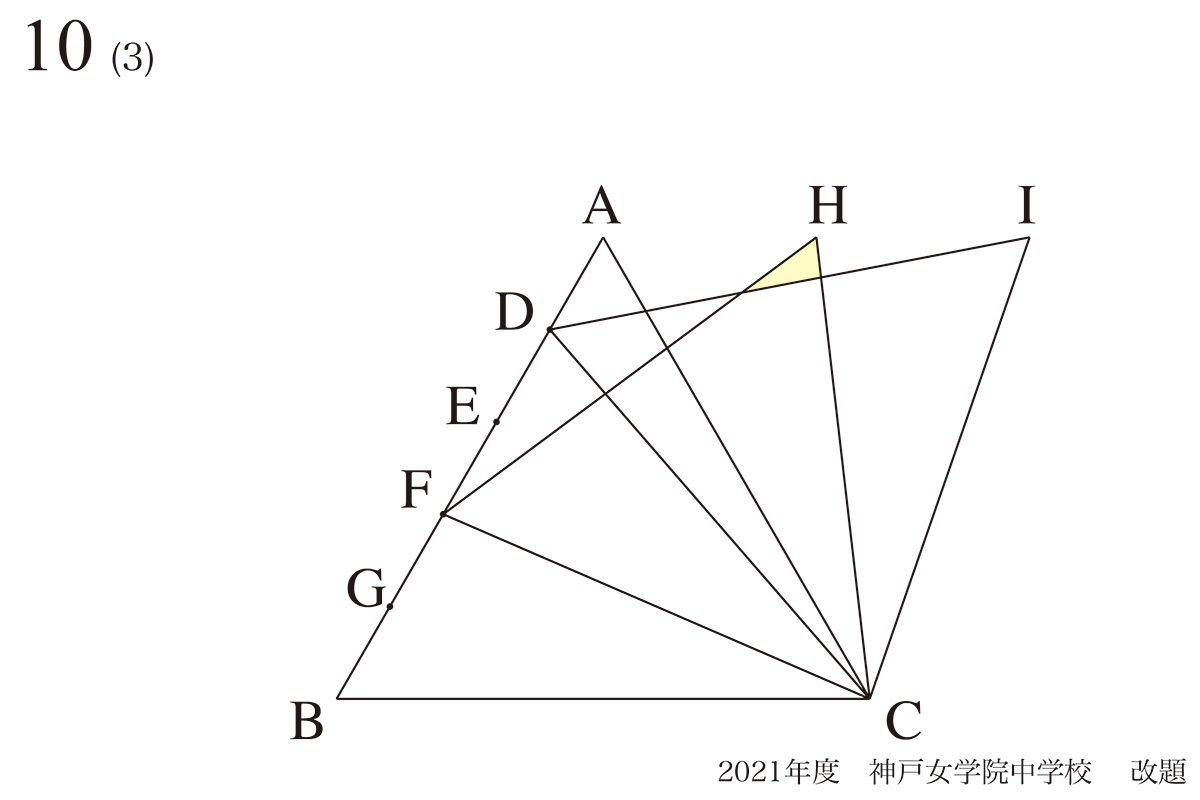
前の問題で分かったことを考える
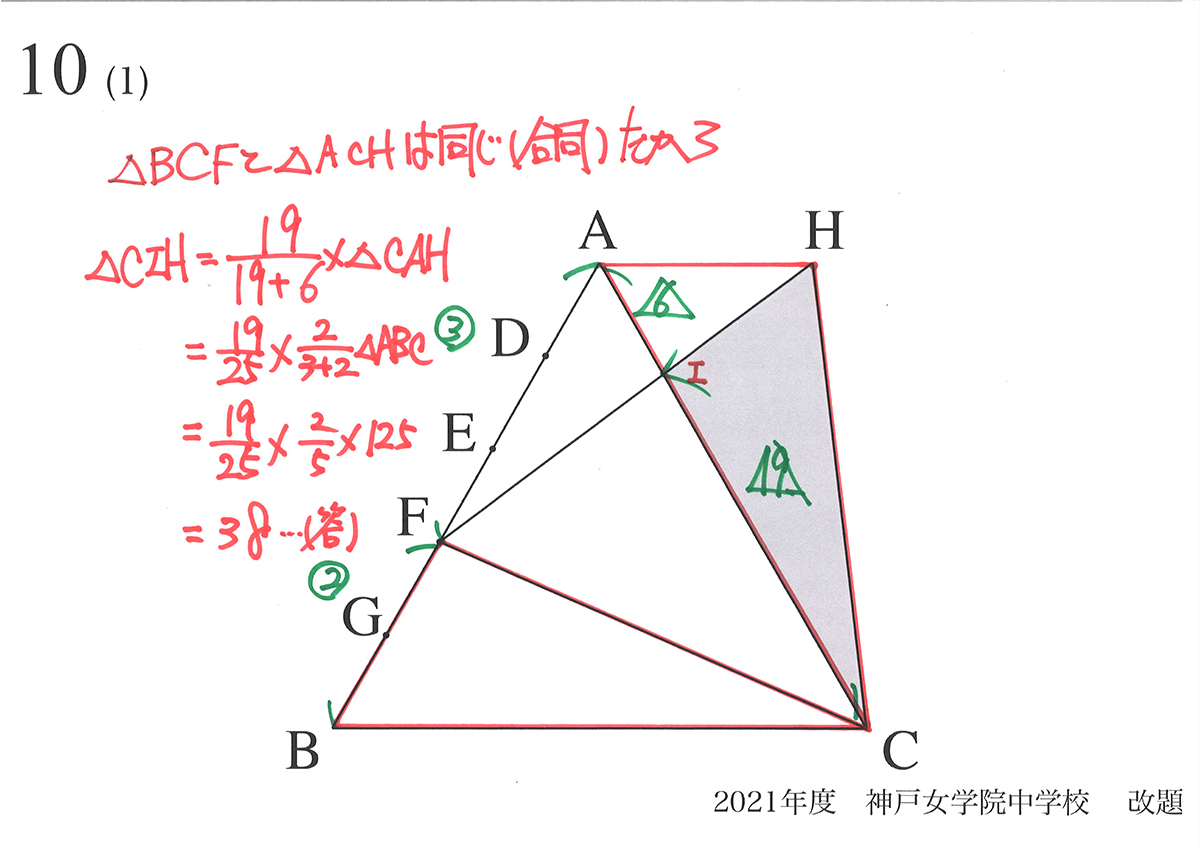
(3)の小さな部分の面積を求めるのに、(1)から考えましょう。
まず(1)で求めた面積38と、そのプロセスで求めた比を確認します。
求める黄色い部分は(1)の面積の一部です。
女子小学生確かに(1)の面積の
一部だけど、とっても小さい・・・
三角形同士の面積比ですから、二つの辺の比が分かれば計算できます。
女子小学生どうやったら、
この小さな部分の面積を求めるための比が分かるのだろう・・・
後ろの問題を考えるときには、前の問題で考えたこと・分かったことを考えましょう。
・前の問題が後の問題のヒント・鍵になっていることが多い
・「前で考えたこと・解いた結果」は常に意識
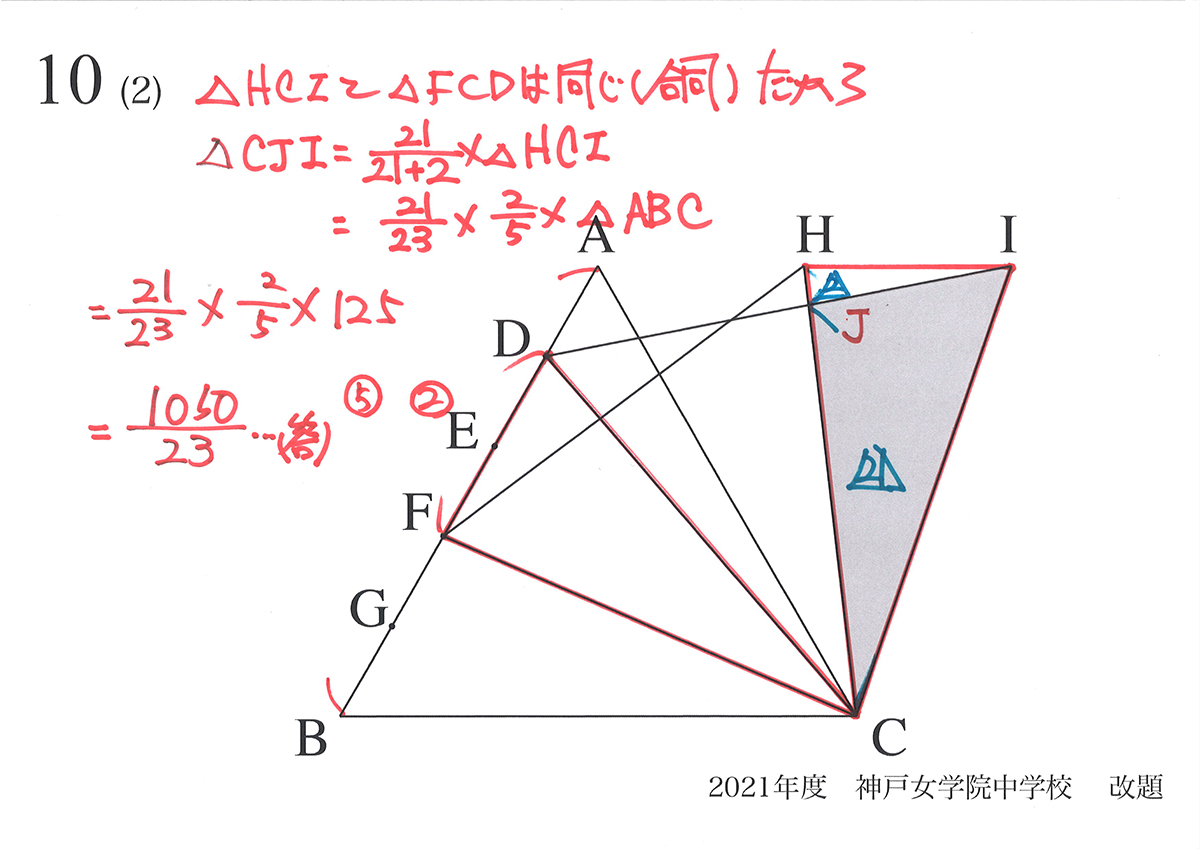
ここで、今度は(2)のプロセスを見直しましょう。
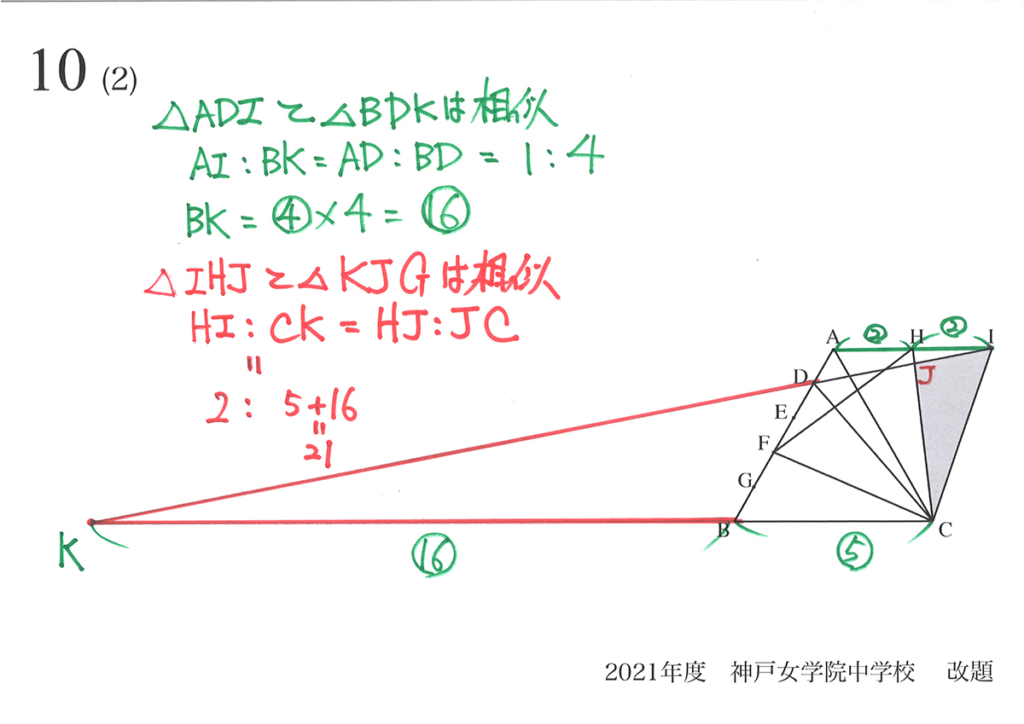
必要な「二つの比」のうち、HJ : JCは分かっています。
男子小学生小さな黄色の面積を求めるために
必要な辺の比は一つ分かっているね！
・一気に考えるのではなく、分かるところから徐々に考えてゆく
・図形に「わかっていること」を描いて整理する
ある部分の面積を求める問題では、
女子小学生どこの辺の比が、
必要かな？
「どの辺の比が分かれば良いか」を考えましょう。
すぐにそれを求めようとするのではなく、
女子小学生今まで考えて、
求めた比で使える比はないかな・・・
「すでに分かっている比の利用」を考えてみましょう。
状況を整理：どの辺の比が分かれば解けるか
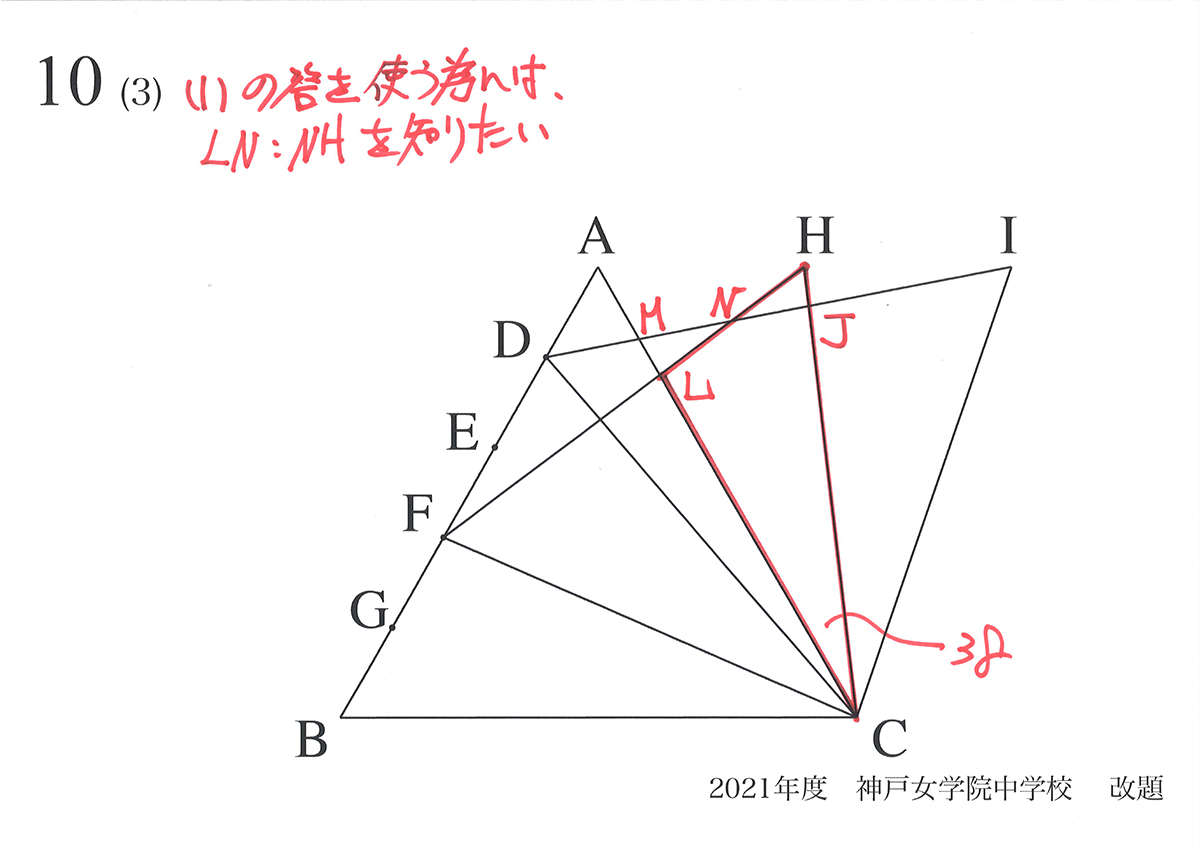
ここまで整理できると、あとはどの辺の比が分かれば良いでしょうか？
上のように点に名前をつけると、LN : NHが分かれば求まりそうです。
記号の振り方は、解答に合わせる必要がなく、「自分なり」で良いです。
自分で必要そうな記号を自由に置いてみて、考えてみましょう。
相似形を考えて、LN : NHを求めるために、手で描いて色々と試行錯誤してみましょう。
なかなか相似形が、見つかりにくいかもしれません。
間違っても良いので考えてみましょう。
ちょっと考えてみて、
男子小学生あ〜ダメだ！
分からないや・・・
このように「すぐ諦めて答えを見る」ではなく、少し考えてみて思考力をつけましょう。
・解答に至らない「無駄なこと」が大事
・「遠回り」や「無駄」を経験すると、試験で「何が大事か」の感覚が磨かれる
この問題ではAH、AIがBCと平行であることが非常に大事なポイントです。
・平行な直線があると、その周辺に相似形がある
・相似形が見つからないときは、自分で相似形をつくる
相似形が見当たらない時は、「相似形をつくる」ようにしましょう。
・平行な直線のうち、一つまたは二つの直線を延長する
・平行ではない直線を延長して、新たな交点を作ると相似形が出てくる
図形問題で行き詰まったときは、
男子小学生相似形を見つけるか、つくれば
解けるはずだ！
「相似形があれば解けるはず」と考える姿勢も大事です。
次回は、LN : NHを求めてみます。
次回は下記リンクです。
