前回は「複雑な図形問題が解けるようになる考え方〜正三角形・動く点P・図形の性質を考える・正三角形はどのように出来てゆくか・何が分かれば面積が求まるか・辺の長さを分割して計算・問題10(2)解法〜」の話でした。
問題 10(3)
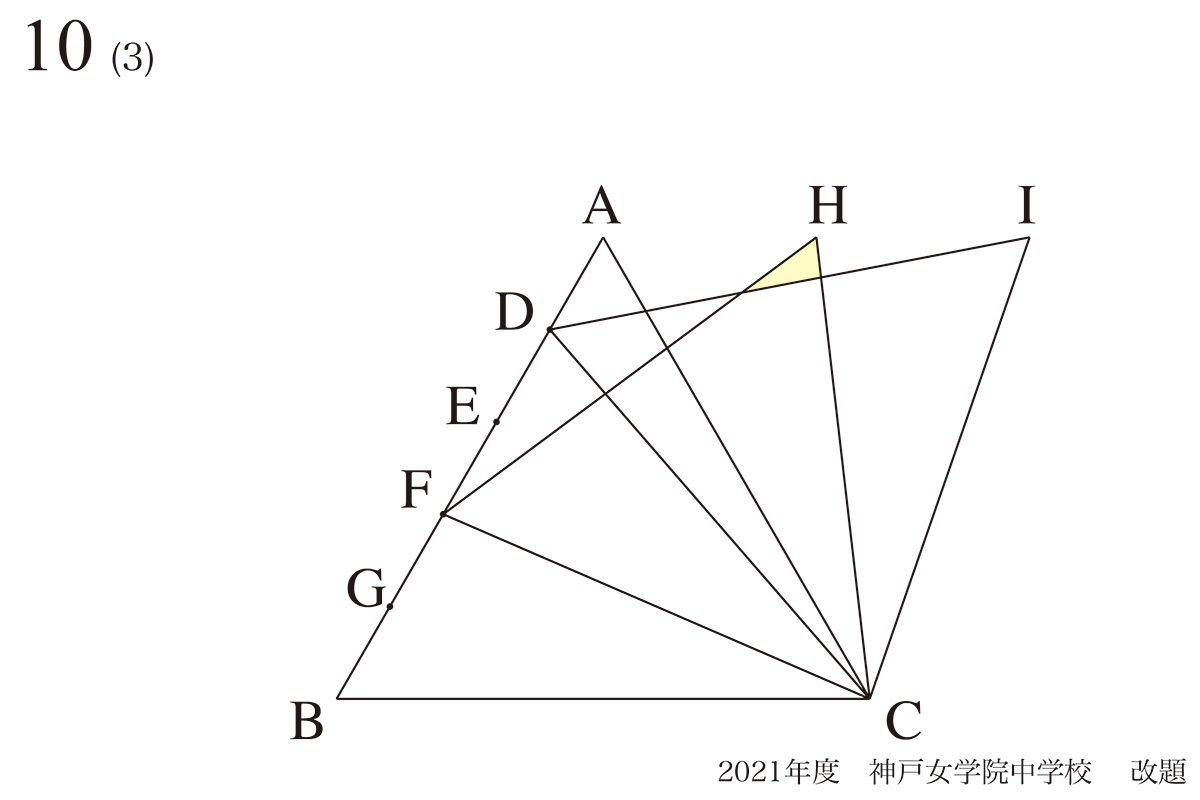
前の問題をヒントに後ろの問題を考える姿勢
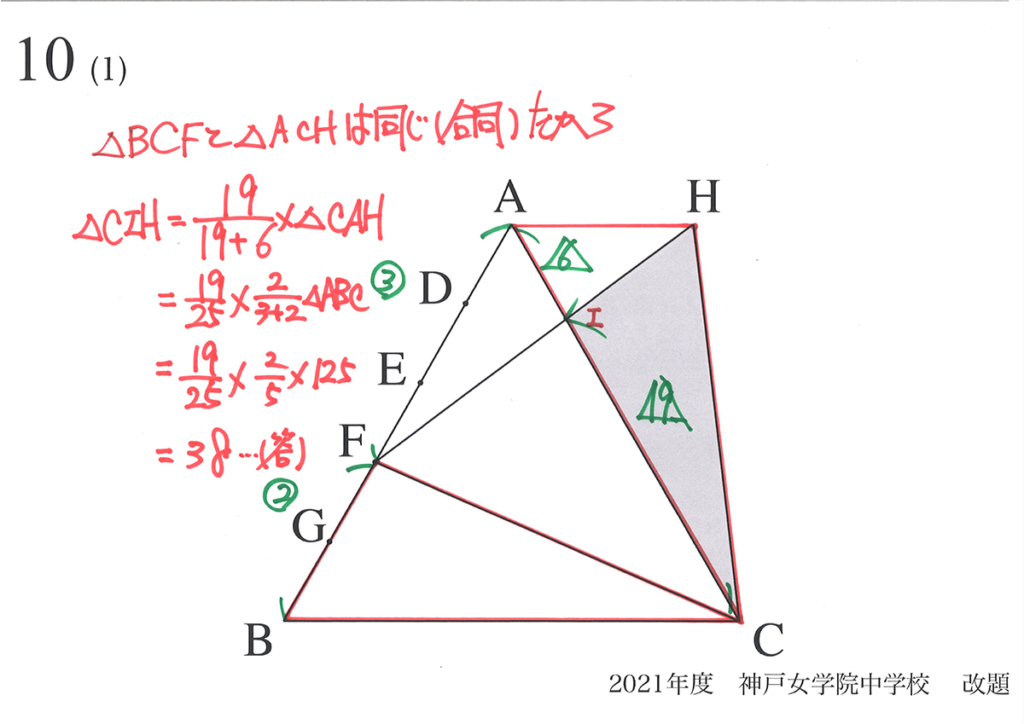
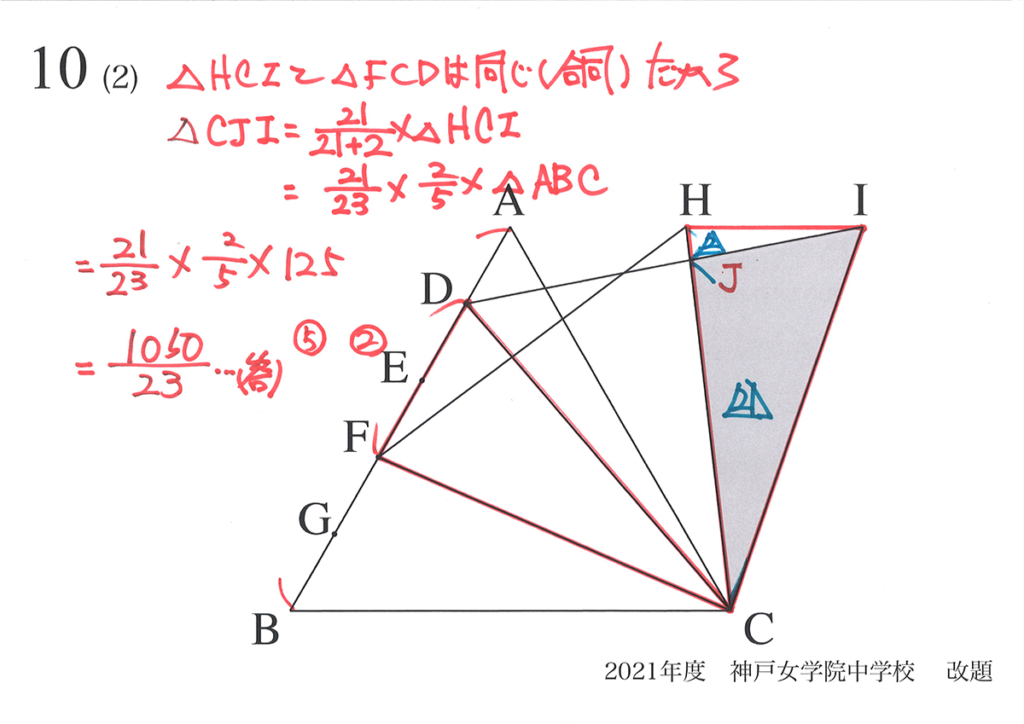
(1)と(2)で「新たに出来る正三角形の一部の面積」を求めました。
今回は創作問題(3)を考えてみましょう。
今回は、(1)(2)同様に「新たに出来る正三角形の一部の面積」ですが、かなり小さいです。
女子小学生こんなに小さな部分の面積を
考えるのって・・・
女子小学生とても難しそうだけど、
出来るのかな？
小さな部分の面積ですが、まずは、
男子小学生(1)か(2)のどちらかで、
求めた面積を使えないかな・・・
すでに解いた問題が使えないか、考えてみましょう。
・一気に考えるのではなく、分かるところから徐々に考えてゆく
・図形に「わかっていること」を描いて整理する
図形問題でも文章題でも、(1)(2)・・・・・と続くときは、前の問題を考えることは大事です。
前の問題が後の問題のヒントになっていることがあります。
特に文章題で「分かりづらい設定」の時は、(1)(2)などで「具体例で考える」ことが出されることがあります。
・前の問題が後の問題のヒント・鍵になっていることが多い
・「前で考えたこと・解いた結果」は常に意識
ちょっと難しい問題に出会った時は、
女子小学生前の問題で考えたこと、解法を
応用できないかな？
このように「前の小問で考えたことの利用」を考えると良いです。
図形の面積：どの辺の比が分かれば解けるか
どちらかを元にすることを考えたら、黄色の部分の面積を求めるためには
男子小学生どの辺の比が分かれば、
良いのだろう？
算数では、このように「何が分かれば解けそうか」を考える姿勢が大事です。
(3)は難問ではありませんが、図形問題の理解力が問われます。
いくつかの辺が交錯する中、きちんと論理立てて進めてゆく力が試されます。
・「問題を解くには、Aが分かれば良い」という「Aを考える」姿勢
・「Aを知るためには、どのようなことが分かればよいか」を考える
・少しずつ、着実に答えに近づいてゆく姿勢
(1)と(2)のどちらから出発しても求められますので、次回は(1)からスタートしてみましょう。
次回は下記リンクです。
