前回は「図形問題が得意になる学び方〜正三角形・動く点Pのイメージ・勘を磨くコツ・寄り道して分かること・好奇心を持って考える・問題10(1)解法〜」の話でした。
問題 10(再掲載)

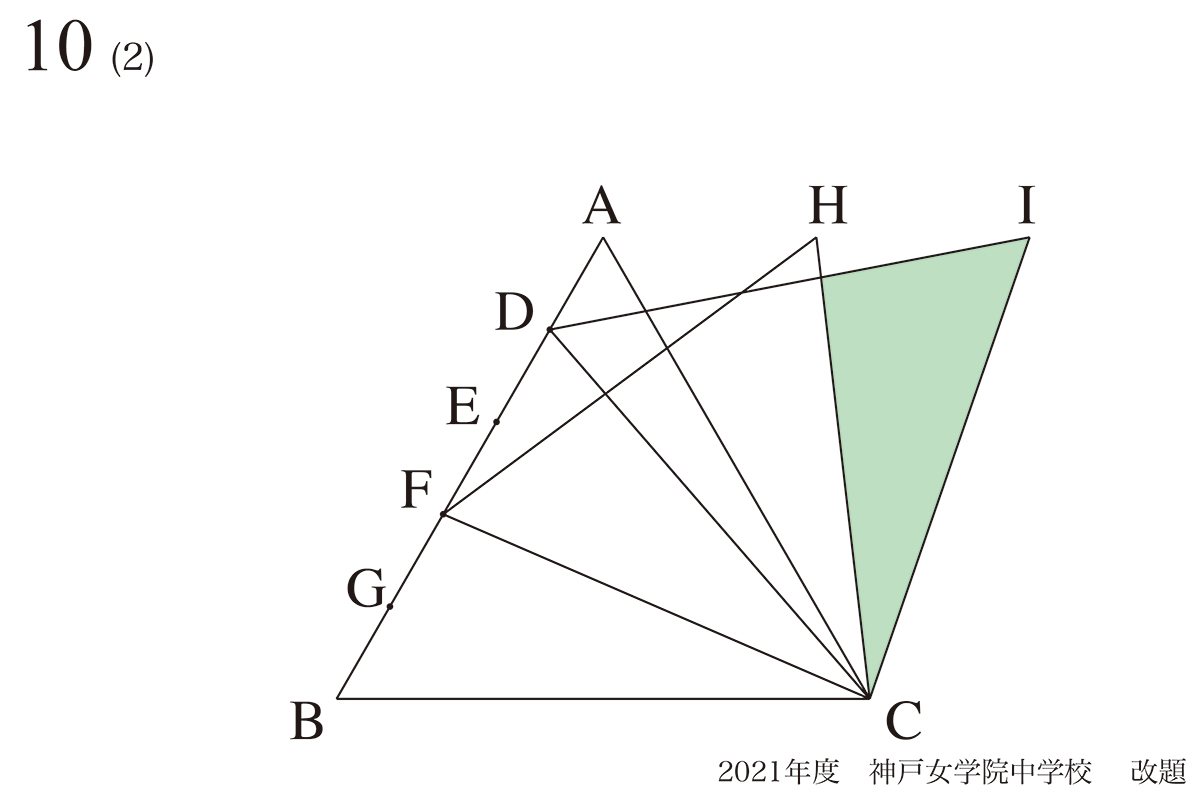
図形問題が「苦手」から「分かる」考え方:類似する解き方
(2)に進みましょう。
(1)と同様に考えてみましょう。
考え方は同様ですが、しっかりと「辺の比と面積比を考えてゆく力」が試されます。
(1)をきちんと理解し、相似形を見つけて着実に考えてみましょう。
「面積を出すには、何を知りたいか?」という具体的に考えてみましょう。
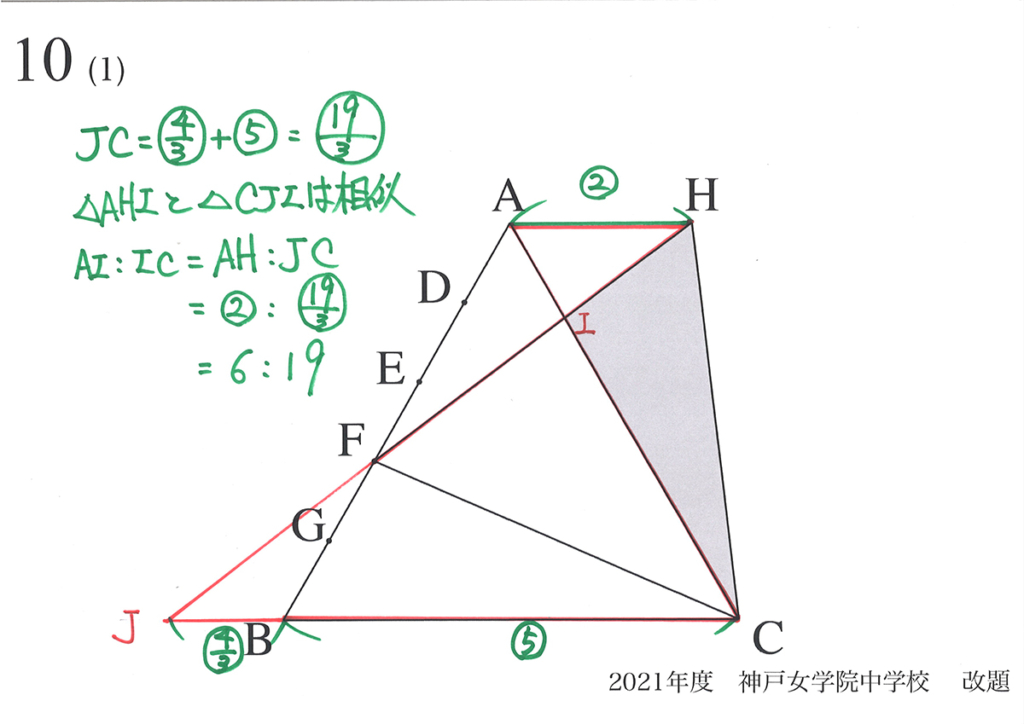
(1)では、「△HICの面積が分かるためには、AI : ICの比を知りたい」と考えました。
このように図形問題に限らず、「問題を解くためには、何が分かればよいか」と考えると良いです。
その何かがわかれば、問題が解けることが多いです。
その何かを知るために、さらに「何かを知る・考える」という問題は難問となります。
いずれにしても、着実に答えに近づいてゆく考え方をしっかり身につけましょう。
・「問題を解くには、Aが分かれば良い」という「Aを考える」姿勢
・「Aを知るためには、どのようなことが分かればよいか」を考える
・少しずつ、着実に答えに近づいてゆく姿勢
正三角形:辺の比と面積比
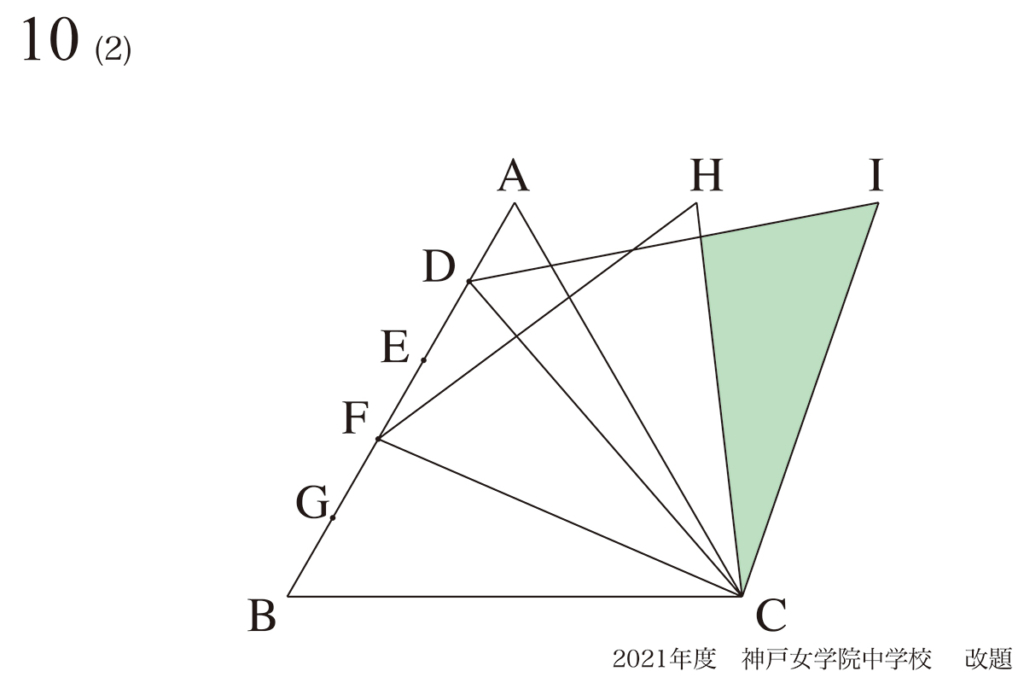
今回は、前回の「新たな正三角形HFCに加えて、さらに新たな正三角形IDC」が登場します。
このように「新たな図形が2つ出てくる」と難しく感じられます。
 男子小学生
男子小学生あ〜あ・・・
難しいよ・・・
こう感じる方もいらっしゃるかも知れません。



(1)と全然図形も違うし、
状況が違うから・・・
「複雑な図形」を前にすると、「この問題は、前の問題と違う」と感じます。
ところが、これらの図形は「同じような考え方で新たな図形・正三角形が出来ている」のです。
すると、「同じように考えれば、出来るのでは」と考えましょう。
・「似た作り方」の複数の図形が登場して、図形が「複雑に見える」時は元の図形の性質を考える
・「似た作り方」の複数の図形に対しては、「似た考え方」が出来るはずと考える
・「違う問題」と考えず「似た解き方」を考える
このように、大問の中の小問は「異なる問題」ではなく「似た問題」と考えましょう。
・求めるものが「面積・長さ・角度」など何でも、まずは「図形の性質」を考える
・点と点を結んで、矢印を考えて「図形の位置関係」を考える
・分かった図形の大事な性質を図形に描きこんで考える
そして、図形問題の基本的な性質を押さえて、少しずつ考えましょう。
すると「大抵の図形問題は出来るはず」です。
次回は下記リンクです。


