前回は「図形問題の解き方・コツ〜正三角形・図形の性質・平行と相似形・「補助線=線を延長」して相似形を作る・図形を少しずつ解明する姿勢・計算過程を明確に・しっかり理解力アップ・問題10(1)解法〜」の話でした。
問題 10（再掲載）
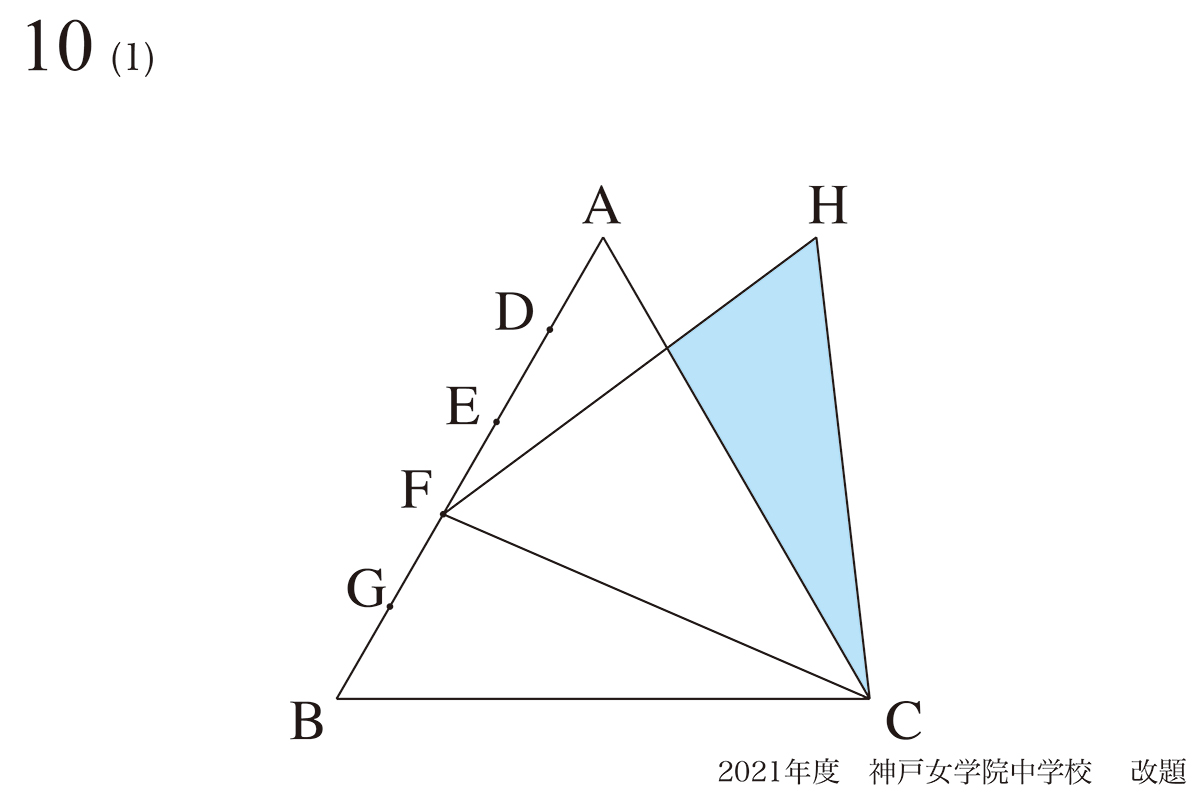
動く点Pのイメージ：勘を磨くコツ
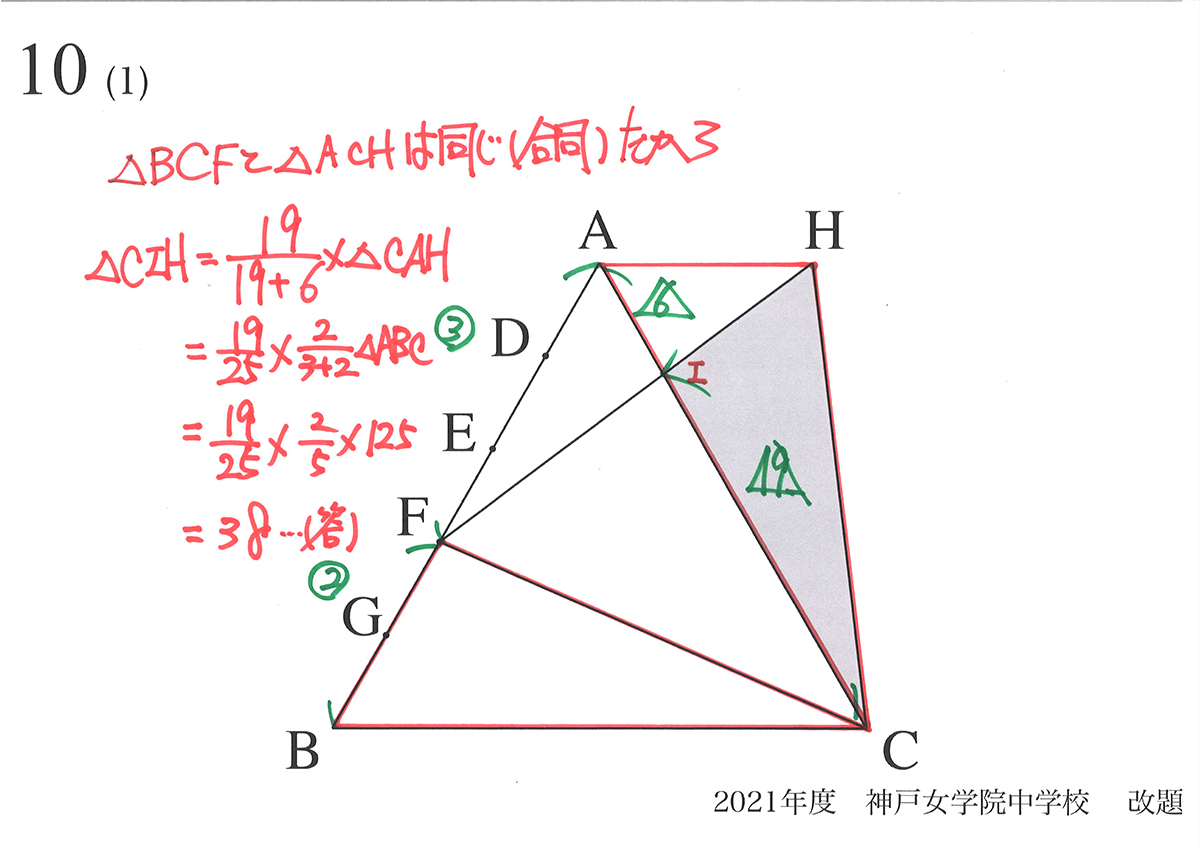
AI : ICの比から△HICの面積を求めました。
(2)に行く前に、ちょっと寄り道して「別の視点」を考えましょう。
「平行な直線」があると、次々に相似形が作れます。
試験当日、図形問題は出来るだけ短い時間で出来た方が良いです。
このような問題では、いくつか解法があります。
実際に自分で色々と考えてみると、
男子小学生こっちが
近道！
あるいは、
男子小学生この考え方は、
ちょっと遠回りかな・・・
このように、自分が実際に色々と考えてみると、解き方が色々な視点から考えられます。
参考書や塾で教えてもらう解法は、大抵は「最も近道」の考え方です。
「近道」の解き方と「遠回りな道」の解き方を自分で手を動かしてやってみましょう。
すると図形問題の様々な側面が分かり、図形問題の勘を磨きます。
女子小学生ここに補助線を
引いてみて・・・
女子小学生あれ、この補助線は
ちょっとイマイチかな・・・
そのうちに勘が磨かれてきて、
女子小学生あっ、この問題は、
こう解く方が良さそうだな・・・
「良い補助線」が、少しずつ分かるようになります。
・解答に至らない「無駄なこと」が大事
・「遠回り」や「無駄」を経験すると、試験で「何が大事か」の感覚が磨かれる
上手い補助線を見つけるコツを、上記リンクでご紹介しています。
理屈で考えるよりも、自分で手を動かすのが最も効果的です。
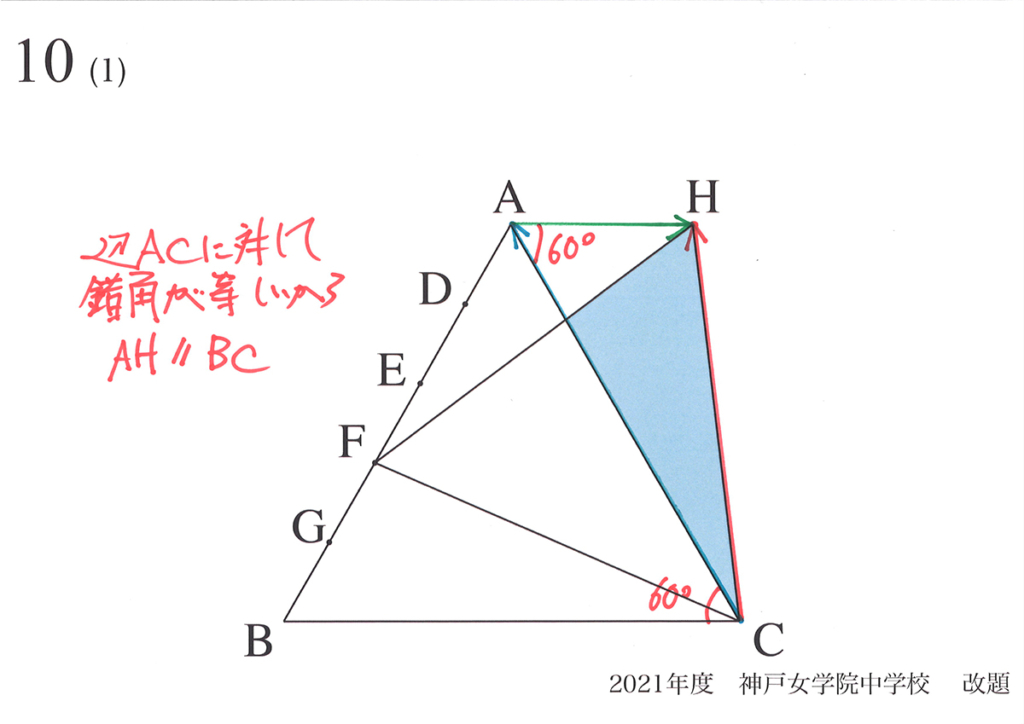
この問題の解法で、「△CBFと△CAHが同じ（合同）」と考えても良いでしょう。
「矢印の考え方」だと、辺BA上の点を取ると、次々と正三角形が出来て行くのが分かります。
この問題では、A,B以外の点D,E,F,Gが固定の点です。
「動く点PがBからAヘ動いてゆく」と考えても良いでしょう。
「AB上のどの点を取っても、正三角形FCHを作ると、AHとBCが平行」です。
男子小学生確かに、
どんどん正三角形が出来て面白いね・・・
女子小学生なんだか、
不思議な感じ・・・
今回は「ABの5等分の点」であり、それによって「AH=BF」となり「AHの長さ」が分かります。
寄り道して分かること：好奇心を持って考える
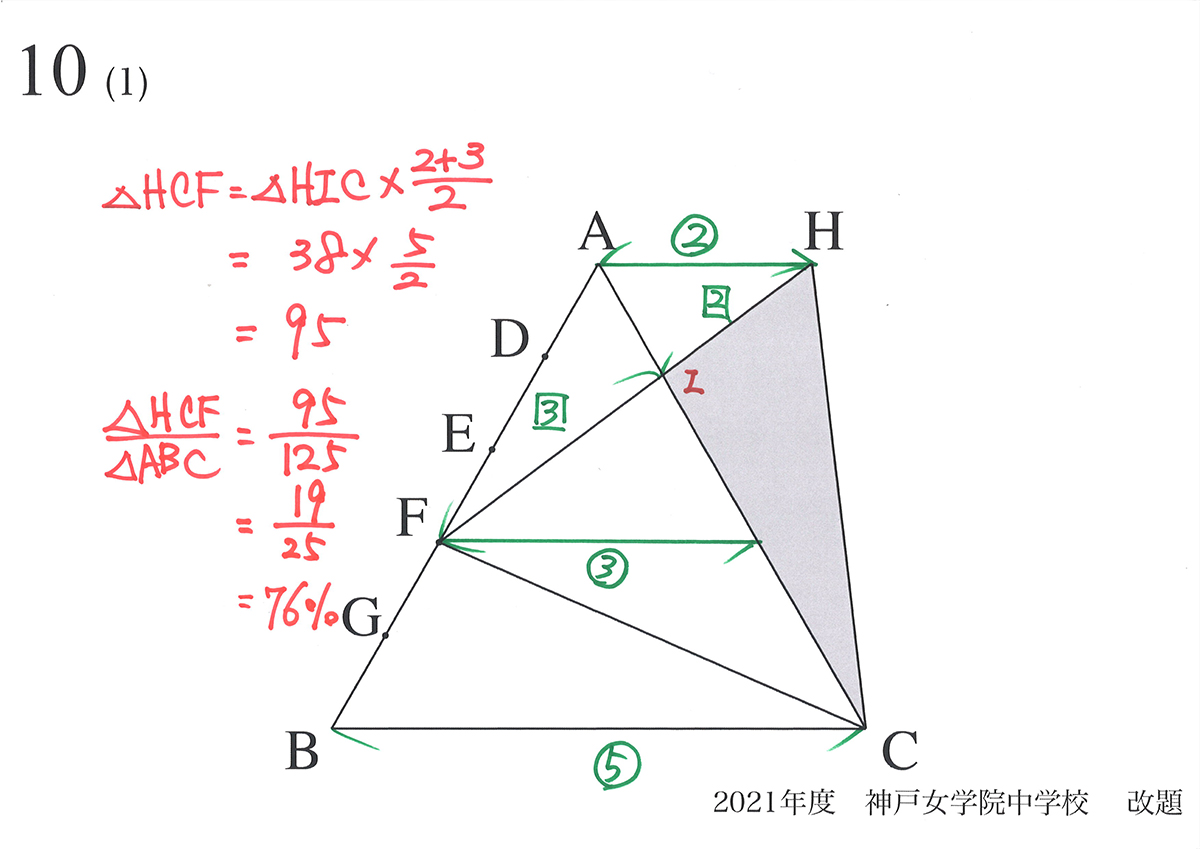
新たに出来た正三角形の面積は、どのくらいになるでしょうか。
計算してみましょう。
上記の通り、面積は95となります。
「もとの正三角形ABCの面積125の76%」になります。
男子小学生元の正三角形の面積より
だいぶ小さくなるね。
女子小学生「76%」というと、
約3/4だね！
細かい数字も大事ですが、「大体〜くらい」とか「約〜」とおよその雰囲気をつかむことも大事です。
問題とは関係ないですが、こういうことも、
男子小学生ここは、
どうなっているのかな？
色々興味を持って、実際に考えてみる姿勢も大事です。
「自分で考えてみる」と図形問題が楽しくなって、どんどん学力が上がるでしょう。
ぜひ、やってみて下さい。
次回は下記リンクです。
