前回は「図形問題が苦手から得意になる矢印の話〜「図書館へ行く」ルート・違うルートで目的地に到着・目的地への二つの異なるルート・同じ位置への移動・問題10(1)〜」の話でした。
目次
問題 10（再掲載）
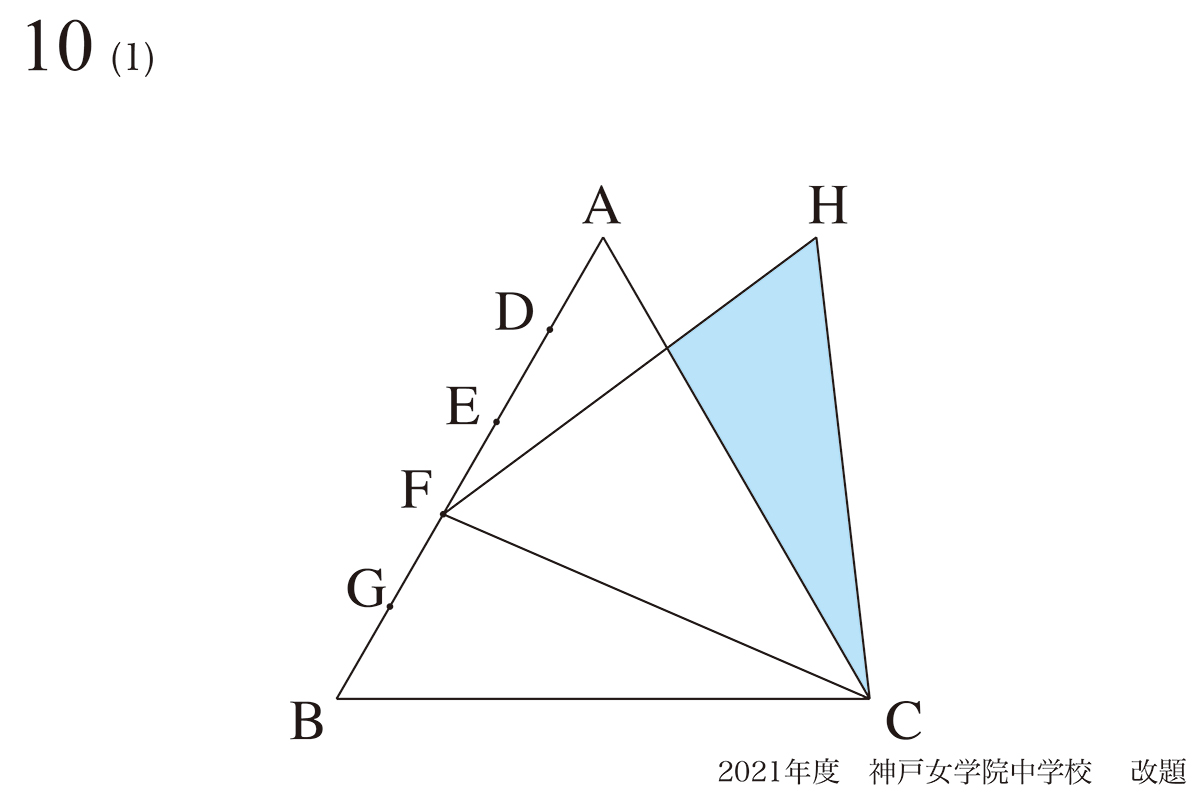
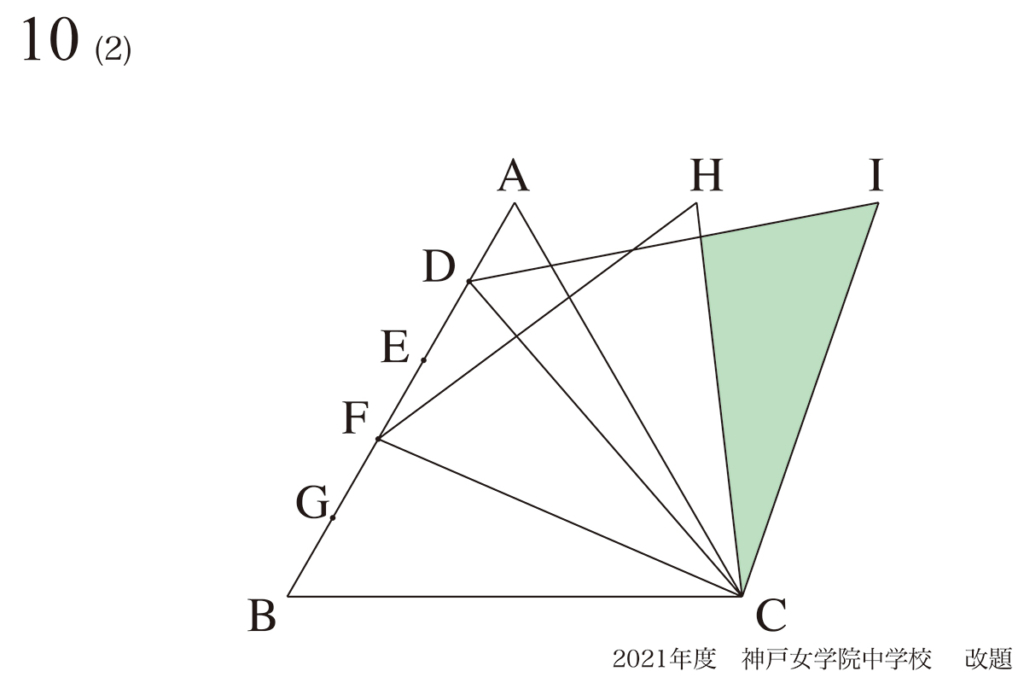
図形を矢印で考える：図形の回転=矢印の回転
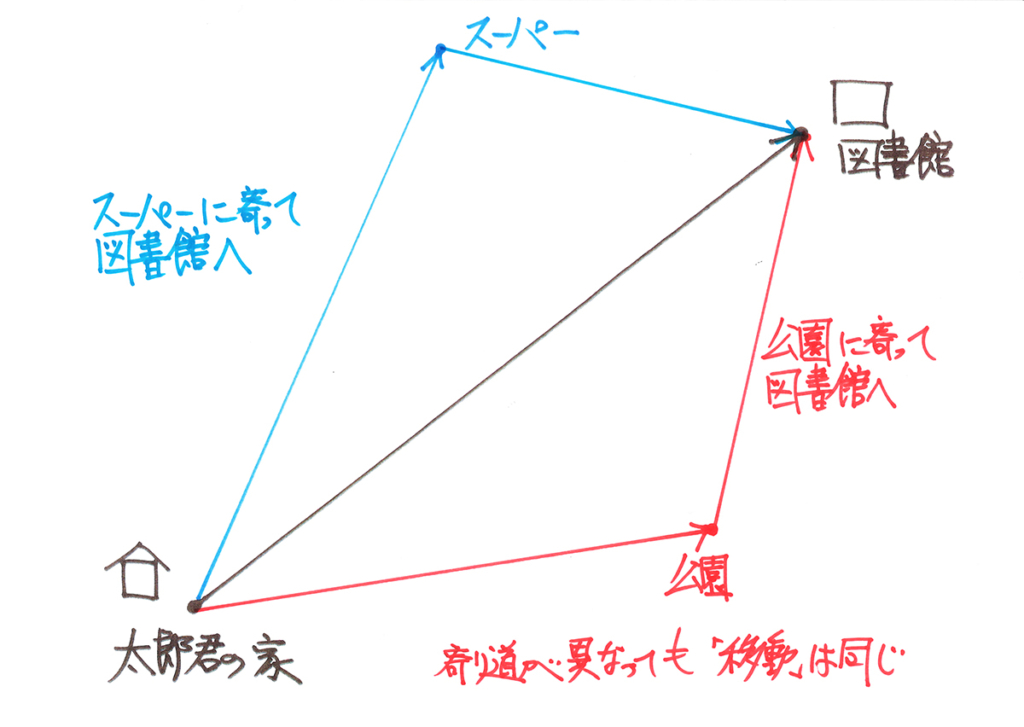
矢印の話
・「ある点から複数の異なるルートである点に移動する」ことは、元の位置関係は同じ
・「ある点からある点へ異なる辺を移動する」ことは、図形的な位置関係は同じ
矢印で図形の点と点の位置関係を考えてみましょう。
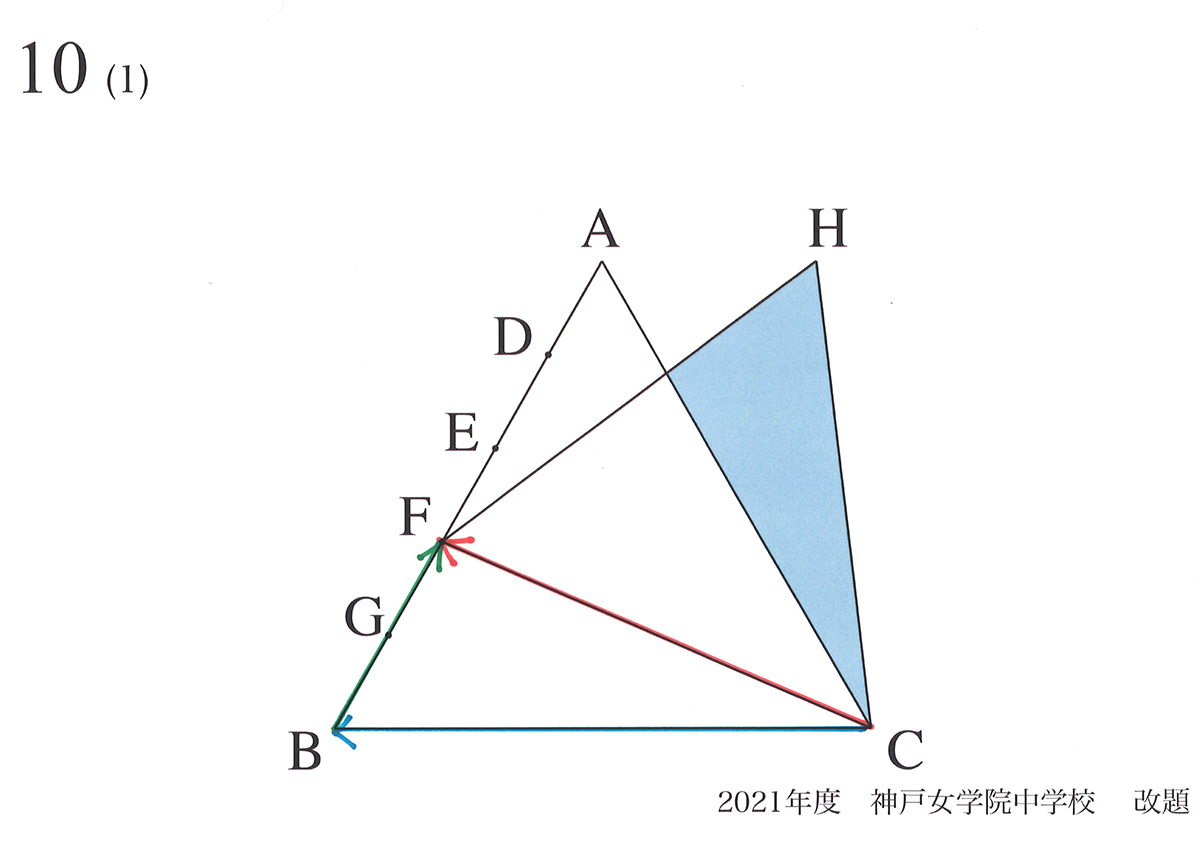
「矢印CF=矢印CB+矢印BF」と考えてみます。
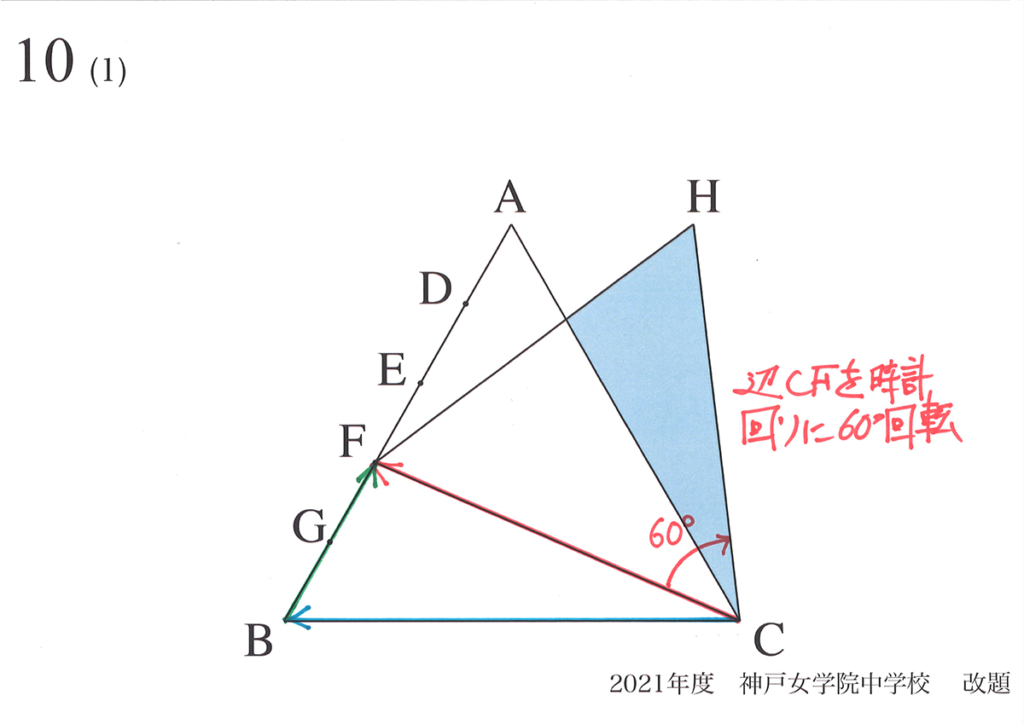
そして、「辺CFを60°回転して辺CHを作る」で正三角形CFHを作りましょう。
矢印CFを回転してみたら、辺AHはどのようになるか考えてみましょう。
女子小学生クルッて
回転させれば良いのかな・・・
矢印から分かる大事な図形の性質
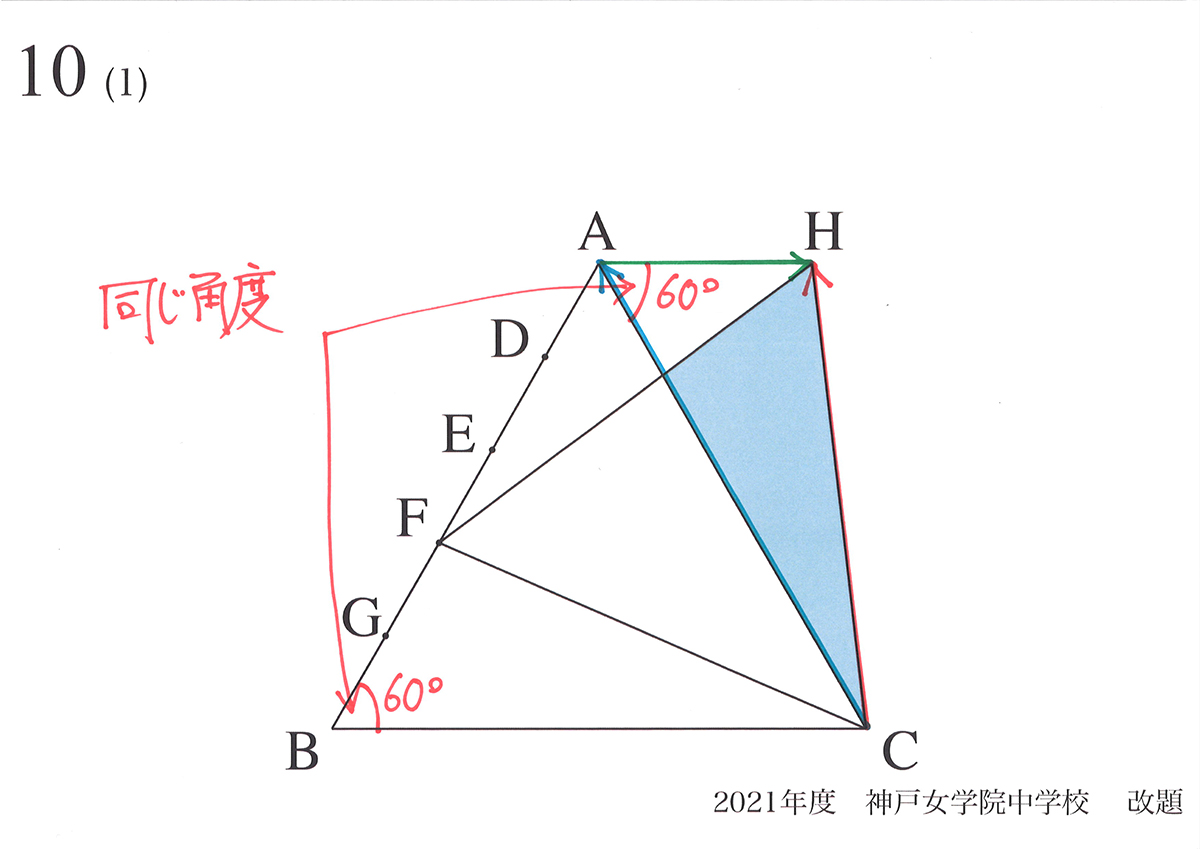
矢印CFを回転すると、矢印CBが矢印CAに、矢印BFが矢印AHに移ります。
女子中学生確かにクルッと
回転させると、そうなるね！
上の図のように角HAC=角BCA=60°となります。
これで「AHとBCが平行」がきちんとわかりました。
もう一つ大事なことがあります。
男子小学生もう一つ
大事なことがあるの？
矢印を回転して正三角形HFCを作ると、矢印BFが矢印AHにちょうど重なります。
男子中学生あっ、そうだ！
分かった！
男子中学生BFとAHの長さが
同じだ！
これも大事な性質です。
男子小学生色々なことが
分かったね！
女子小学生色々分かって、
解けそう！
これで、本問の鍵は全部解りました。
ここから、しっかり面積を求めてみましょう。
次回は下記リンクです。
