前回は「おすすめ図形問題の解き方〜図形・正三角形の性質・「正三角形を作る」こと・見えてくる「大事な性質」・60°回転と平行・問題10(1)〜」の話でした。
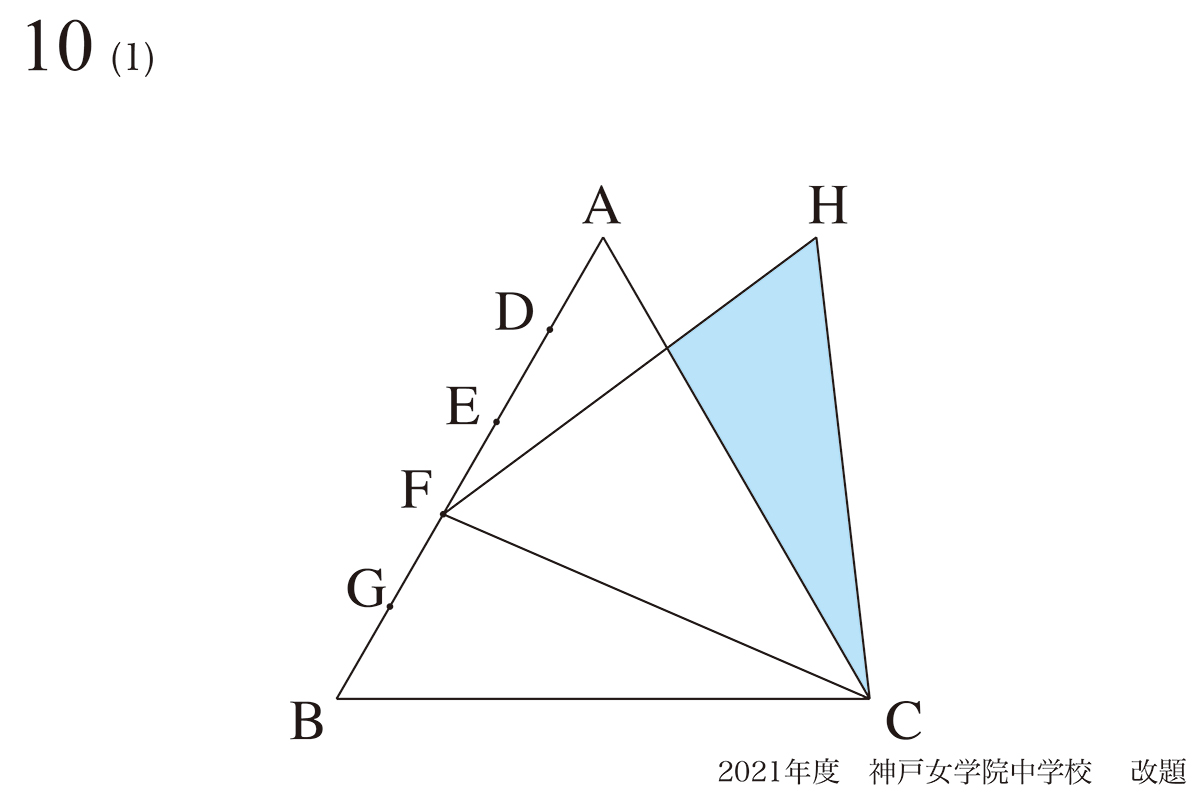
問題 10（再掲載）
図形と矢印の話：「図書館へ行く」ルート
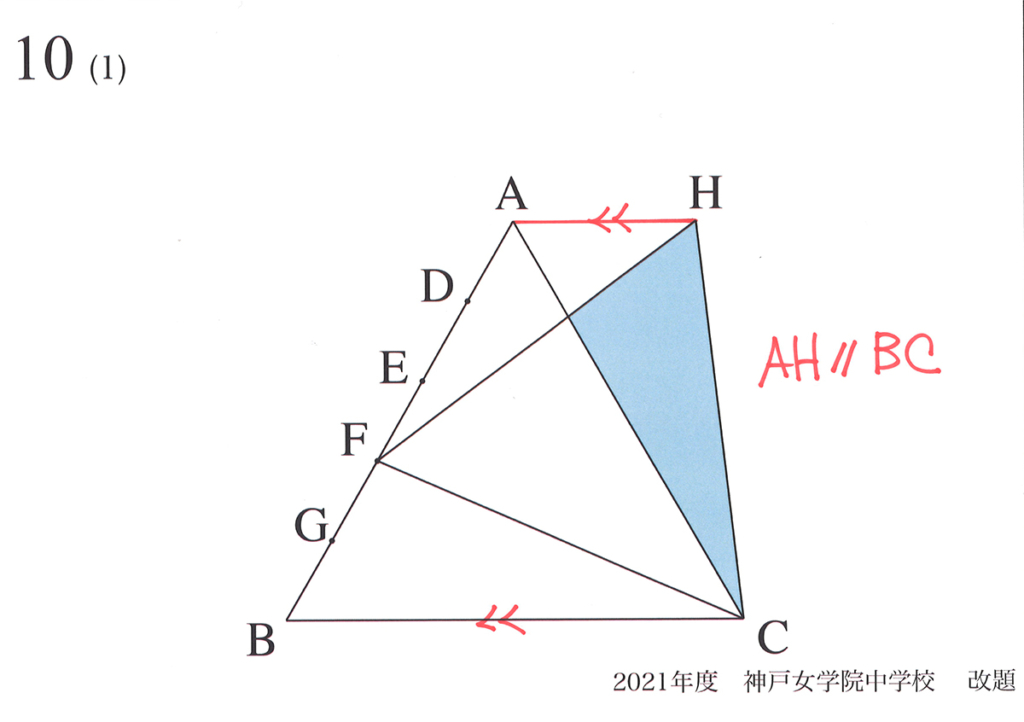
この問題を「解く鍵」となる「AHとBCが平行」の話でした。
今回は「矢印の話」です。
内容は小学生の算数の範囲を超えますが、基本的概念は知っていて良いと思います。
太郎君がお母さんと一緒に図書館に行くことを考えましょう。
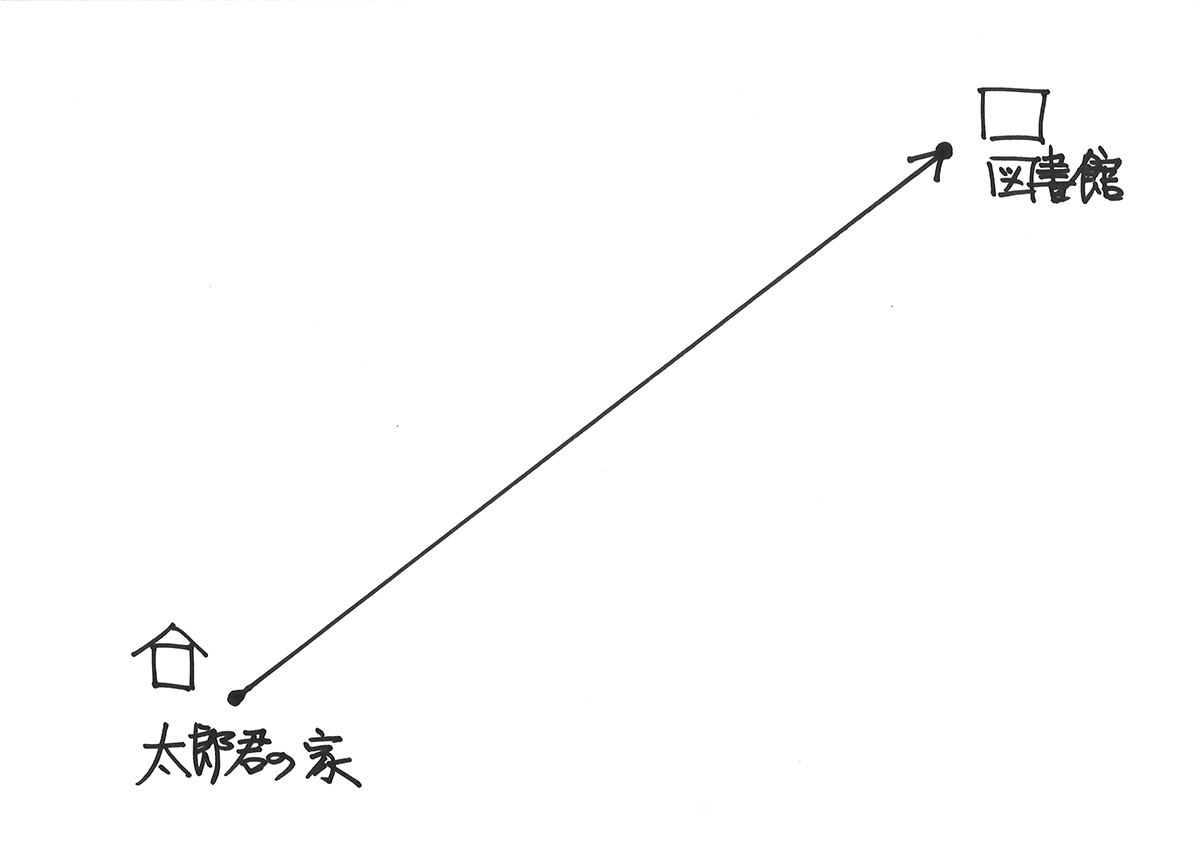
実際には道路などで道は変わりますが、「大体の感じ」で考えて下さい。
そして、ここでは移動時間・歩く速さなどは考えず、「移動する図形的位置関係」のみ考えます。
太郎君ちょっと公園のブランコで遊んでから、
図書館で本読みたい！
と太郎君が言うので、先に公園に寄りました。
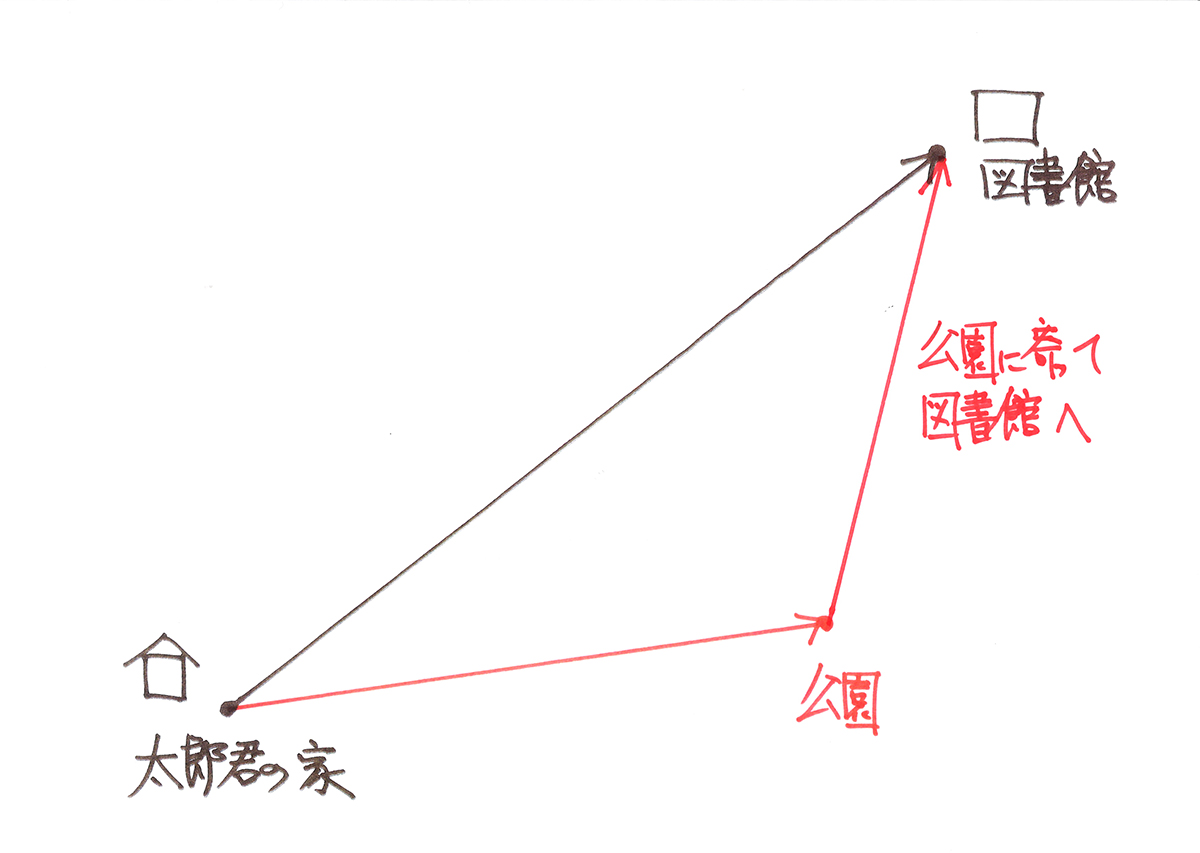
そして、公園から図書館に向かいました。
ブランコでちょっと遊んで大満足の太郎君は、手を洗ってお母さんと一緒に図書館に行きました。
違うルートで目的地に到着
違う日に、太郎君がお父さんと一緒に図書館に行くことになりました。
太郎君今日はちょっと
咳が出るよ・・・
太郎くんの父親そろそろ花粉症の
時期だからね・・・
太郎くんの父親ちょっとのど飴買ってから
行こうか！
太郎君うん！
飴舐めたい！
家を出た太郎君がちょっと花粉症気味なので、のど飴を買うために先にスーパーに向かいます。
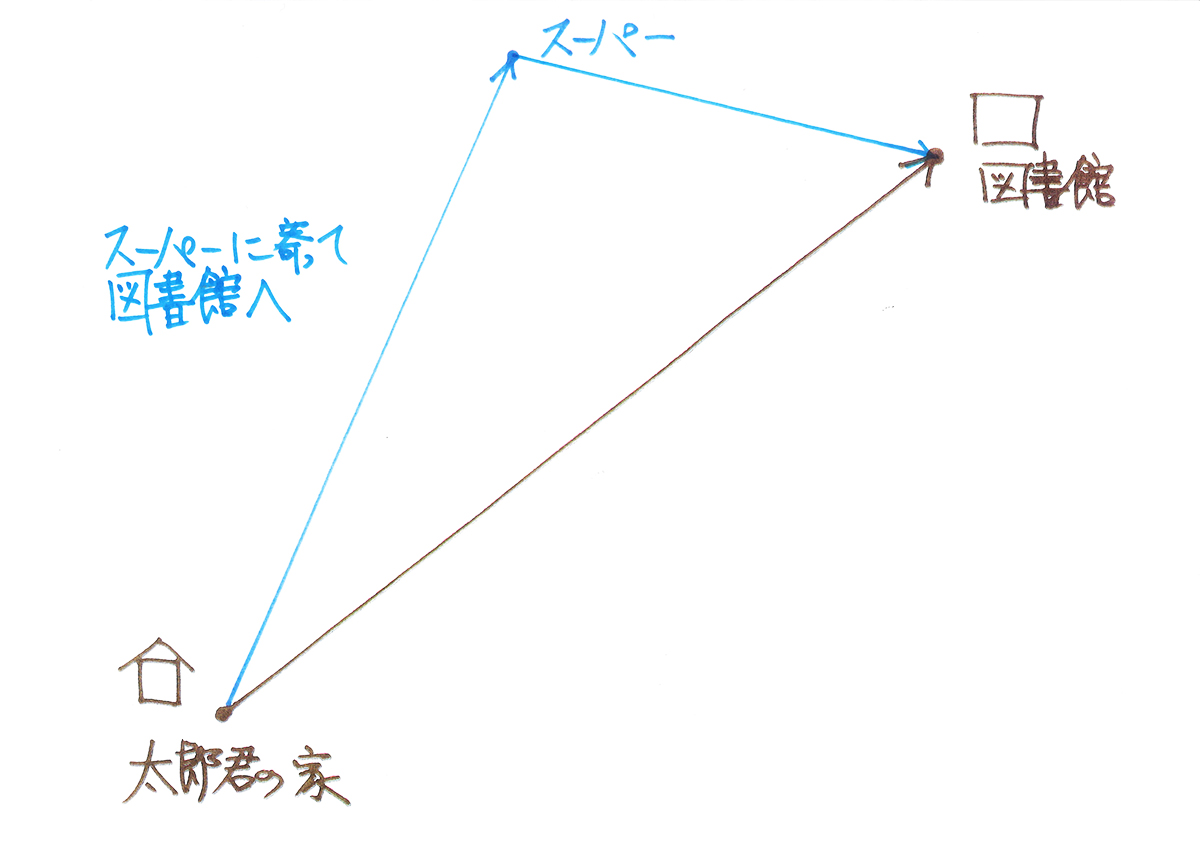
スーパーでのど飴買って、図書館に向かいます。
目的地への二つの異なるルート：同じ位置への移動
男子小学生僕だったら、
コンビニに寄ってから行きたいな！
女子小学生私だったら、
真っ直ぐ図書館に行く！
これ以外にも、様々なルートが考えられます。
「移動した位置関係のみ着目」しましょう。
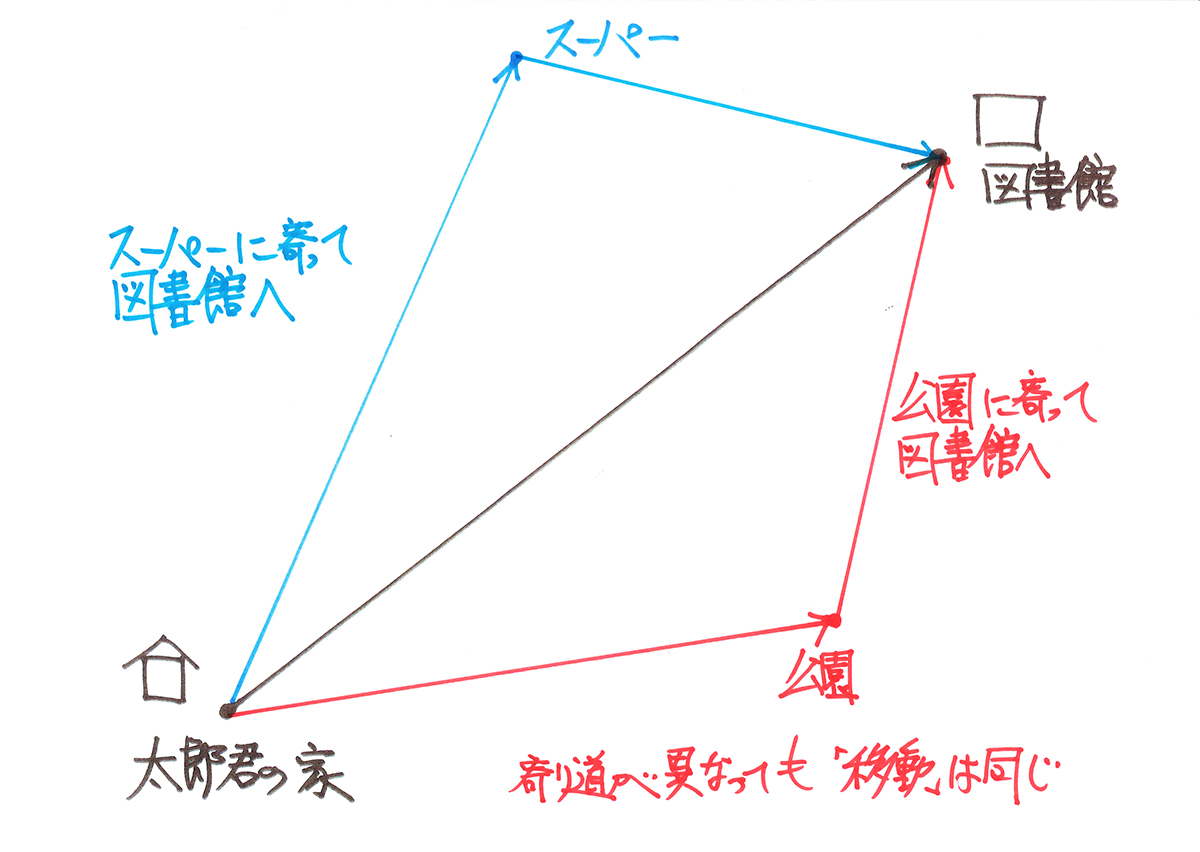
「ルートが変わっても、太郎君の家から図書館に行った位置関係は同じ」です。
これは、もともと太郎君の家と図書館の位置が「変わらない」のですから、「当たり前」の話です。
「当たり前」かも知れませんが、この「目的地への異なるルートが同じ」は図形で大事な性質です。
・「ある点から複数の異なるルートである点に移動する」ことは、元の位置関係は同じ
・「ある点からある点へ異なる辺を移動する」ことは、図形的な位置関係は同じ
同じように、この問題で考えてみましょう。
点と点の位置関係を「矢印をつなげてみる」と何か見えてきませんでしょうか。
少し図を描いて、矢印を描いてみましょう。
男子小学生矢印で
寄り道する感じかな？
女子小学生この点とこの点を
結んで・・・
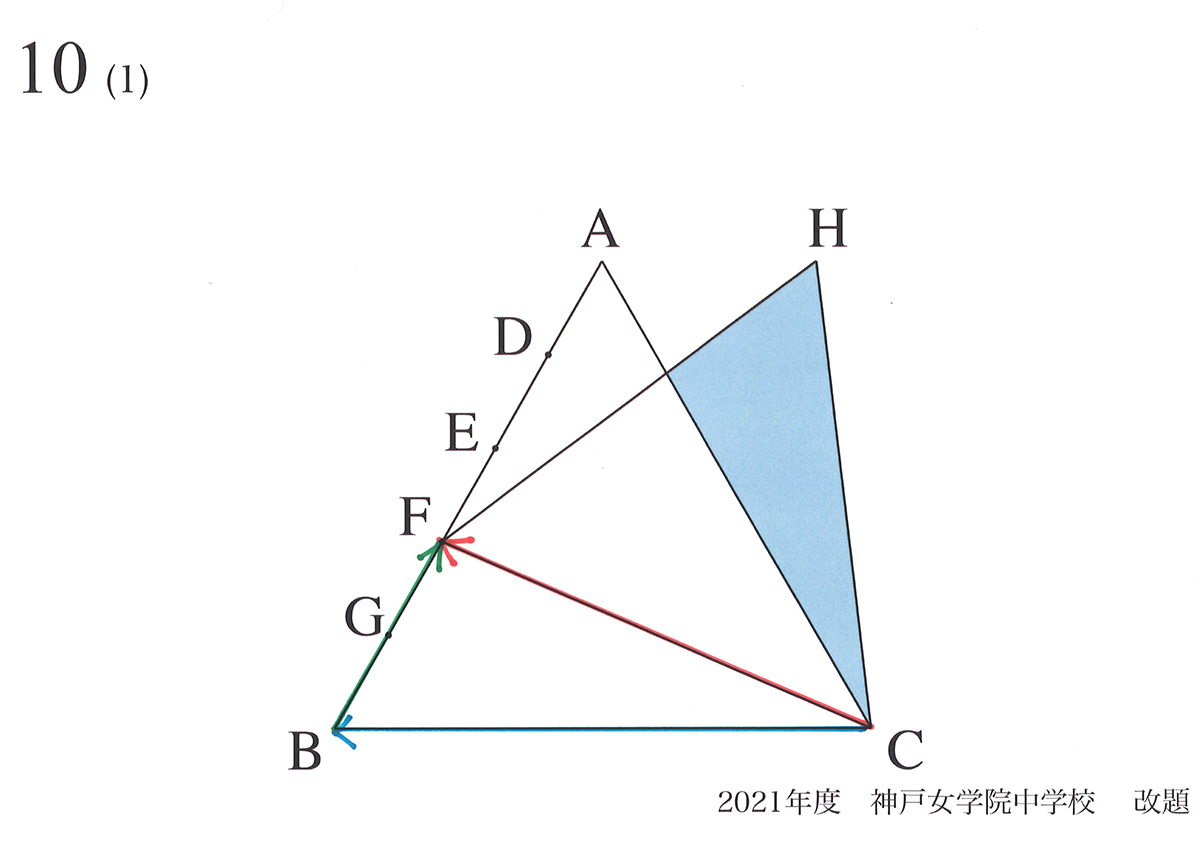
「点Cと点Fの位置関係」は「点Cから点Bへ行って、点Bから点Fヘ行っても同じ」です。
「辺CFの矢印=辺CBの矢印+辺BFの矢印」と考えてみましょう。
女子小学生なるほど、
面白いね！
すると、何か見えてきませんか。
男子小学生確かにそうだけど、
特に何かわからないけど・・・
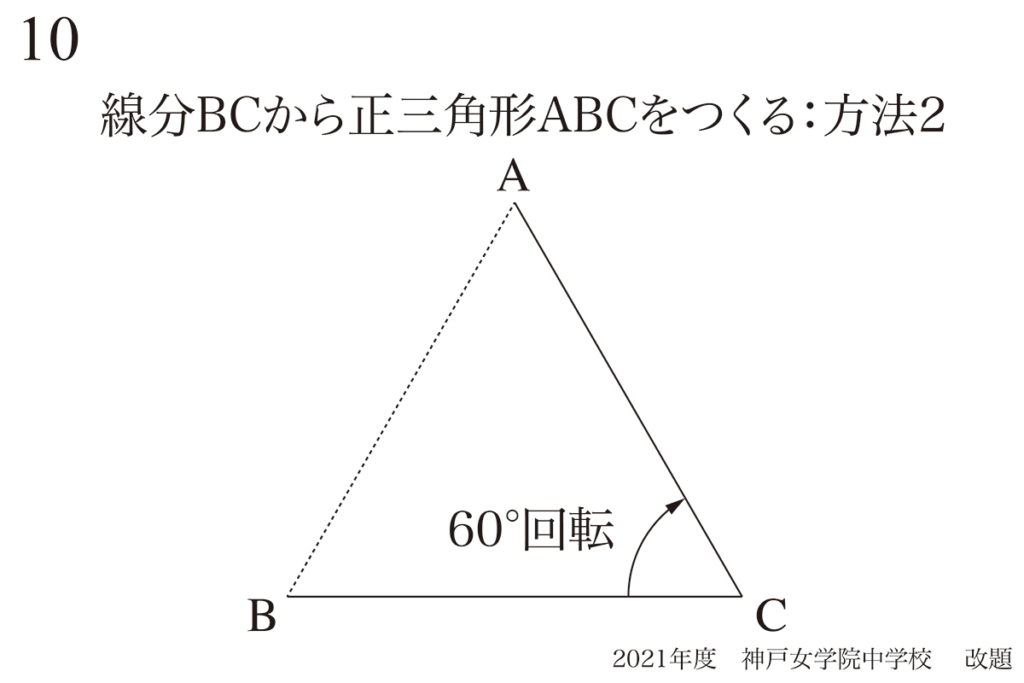
「正三角形を作る=辺を60°回転」を考えてみましょう。
色々と自分で描いてみて、楽しく試行錯誤してみましょう。
次回は下記リンクです。
