前回は「正三角形の基本的性質〜正三角形の描き方・作り方・特殊な図形の大事な性質：正方形・円・正六角形・問題10(1)〜」の話でした。
問題 10（再掲載）
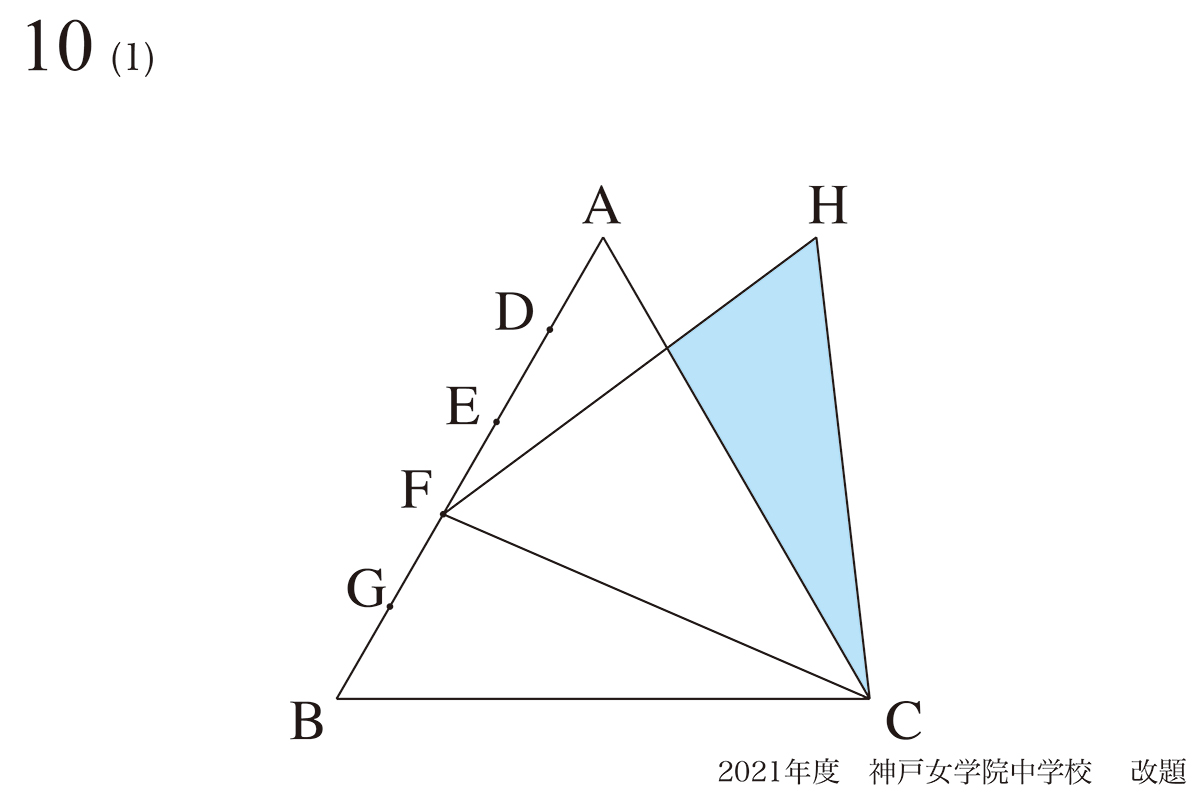
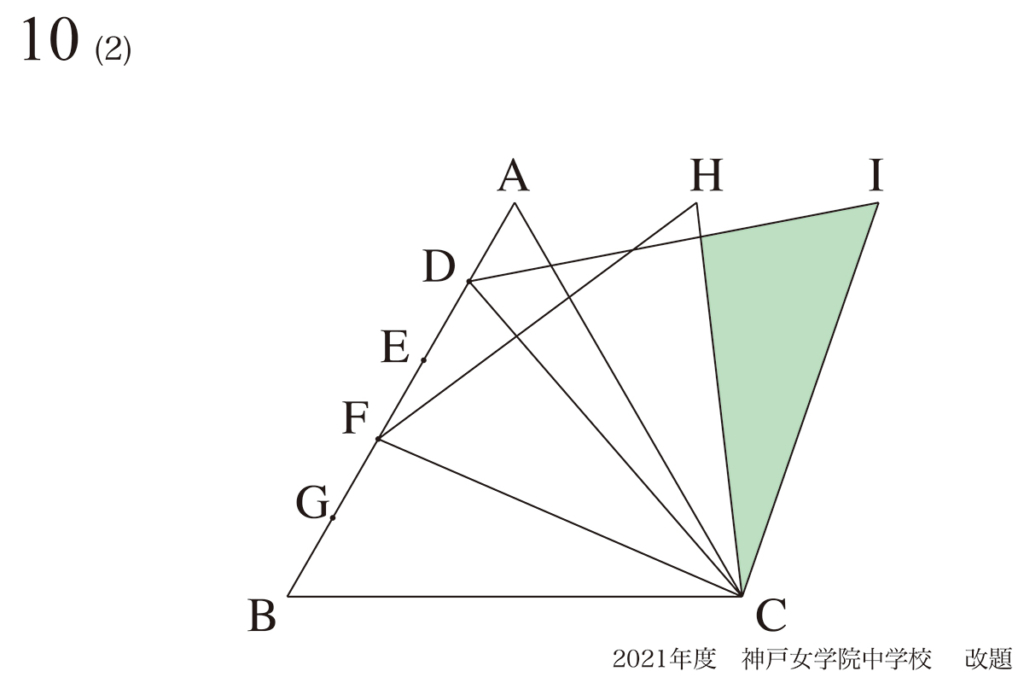
正三角形の描き方・作り方A：コンパスで同じ長さ作成
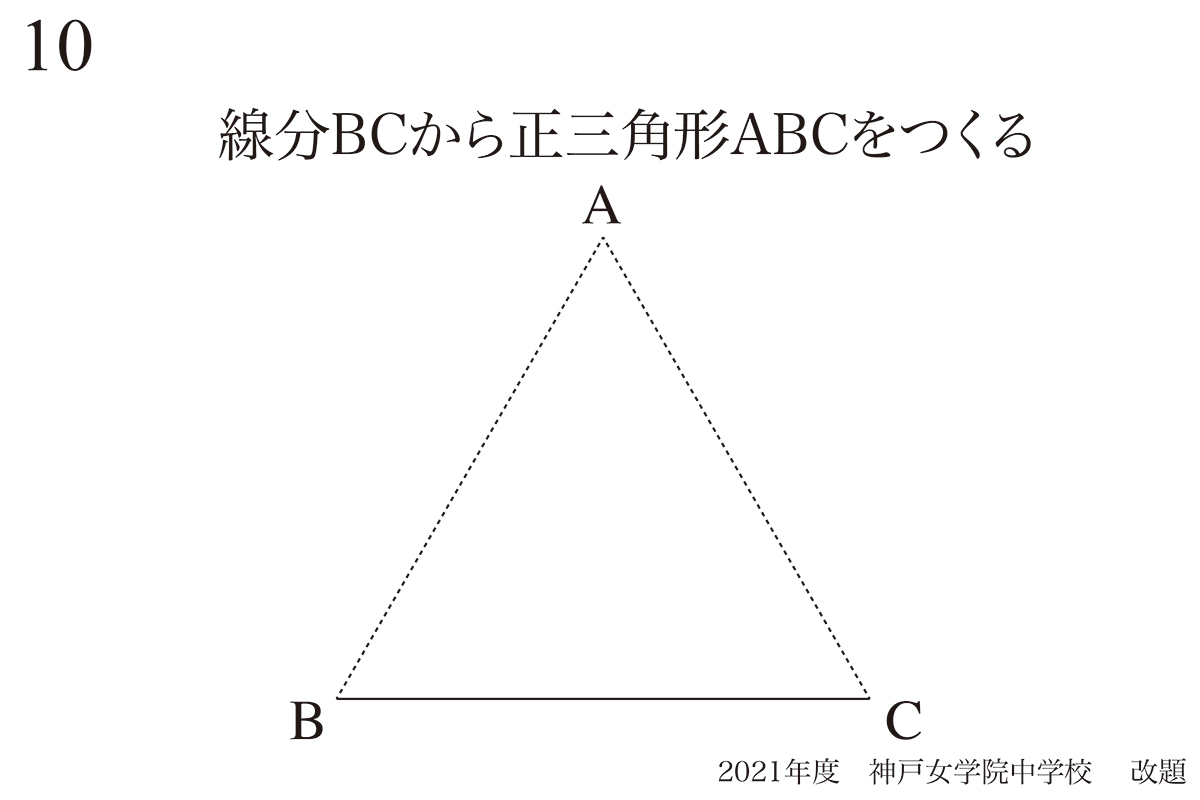
解き方に行く前に「正三角形の本質的性質」を考えましょう。
上の図形をご覧ください。
辺BCがある時、辺BCの上部にAをとって、正三角形ABCを描いてみましょう。
一つ目の描き方は、「正三角形=三つの辺の長さが等しい三角形」から考えます。
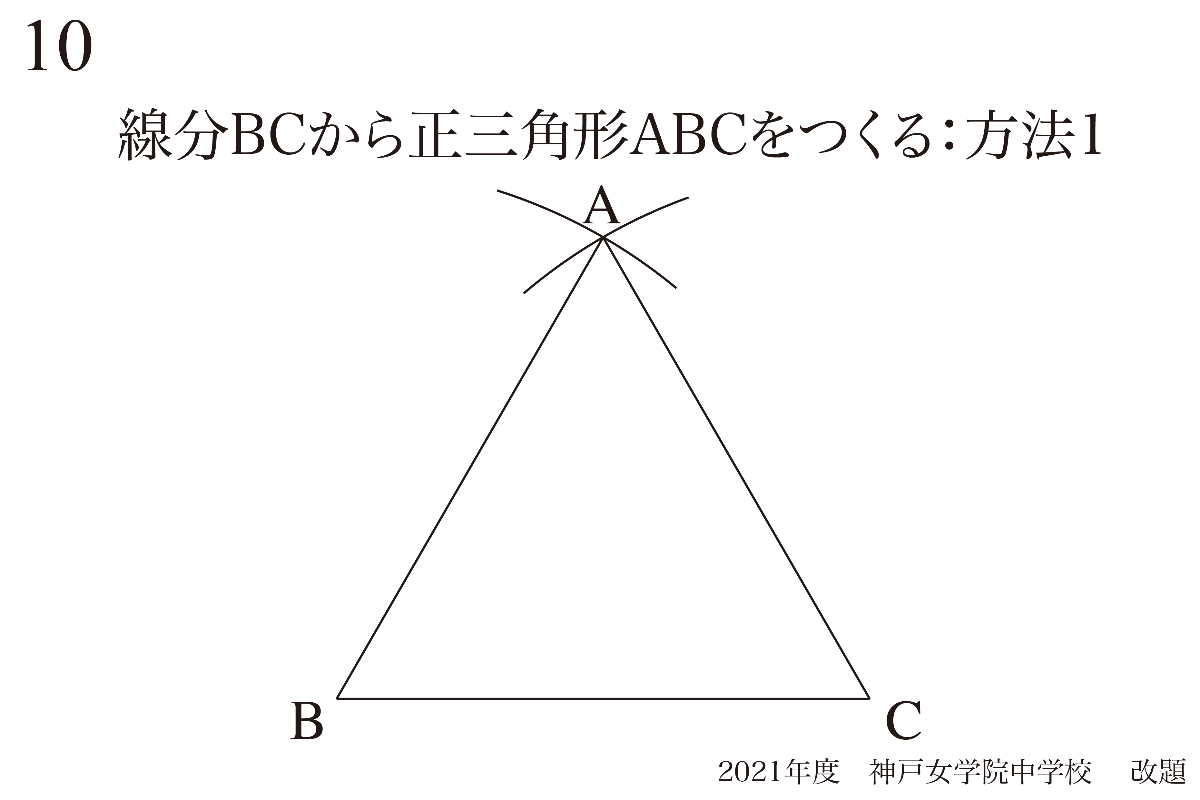
B,CからコンパスでBCの長さをとって、Aを求めます。
男子小学生これは、
すぐに分かったよ！
女子小学生小学校でコンパスの使い方を
習った時に、描いた！
「異なる視点」や別解を習得：問題を解く視野を広げる
もう一つ考えてみましょう。
男子小学生一つ出来れば
いいんじゃないの？
ある問題・考えに対して、複数の考え方がある時、そしてそれらの考え方が「異なる視点」の時。
それらの「異なる視点」をしっかり理解することは、問題をたくさん解くより効果的です。
算数の問題で、別解を習得することも大事なことです。
・「異なる視点」をしっかり理解
・「異なる視点」は視野が広がり、応用問題への力が強化される
・異なる視点や別解を習得することは、問題をたくさん解くより効果的
正三角形は「三辺が全て等しい」以外にも、様々な基本的性質があります。
「全ての角が等しい（60°）」です。
・全ての辺の長さ・角度が同じ
・対称（折り返したら同じ）となる軸がたくさんある
・回転対称性（中心・重心で回転すると同じ）がある
この性質をもう一度考えてみましょう。
上記以外の方法が分からなかった方は、先に進む前に少し考えてみましょう。
正三角形の描き方・作り方B：一辺を60度回転
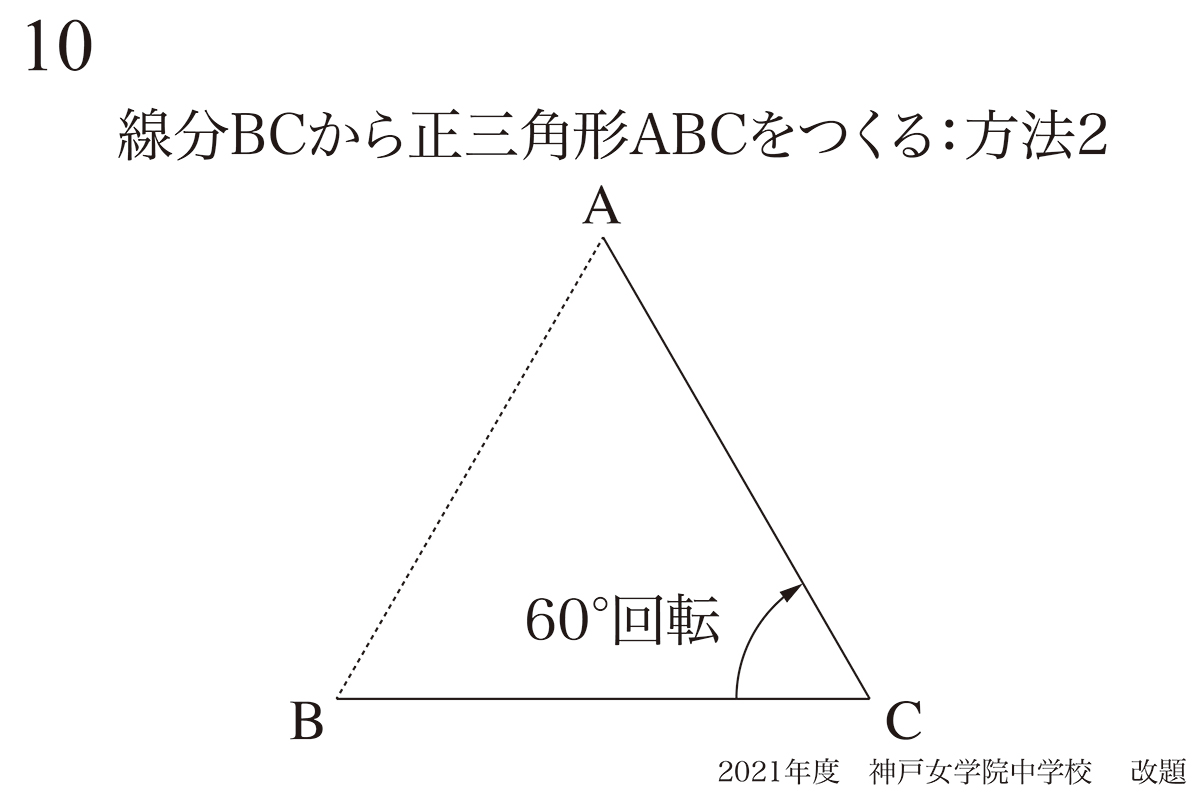
角度が分かっていますから、辺BCを60°時計回りに回転したら、辺ACになります。
60°は、三角定規を使えば分かります。
男子小学生なるほど！
確かにそうだね！
この性質は、
女子小学生当たり前だと
思うけど・・・
「当たり前」と思うかもしれませんが、非常に大事です。
正三角形の基本的性質は、「すべての辺の長さ・角度が等しい」です。
さらに、この「一辺を60°回転（左回り・右回り）」は、頭に入れておくと良いでしょう。
この「正三角形の本質的性質」を考えて、問題10(1)を考えてみましょう。
次回は下記リンクです。
