前回は「回路のわかりやすい考え方・解き方 2〜電流の流れ ・電流の流れと高さ・電流がグルッと・「電流は抵抗の逆比」を理解〜」の話でした。
回路を難しく考えない姿勢：理解する姿勢
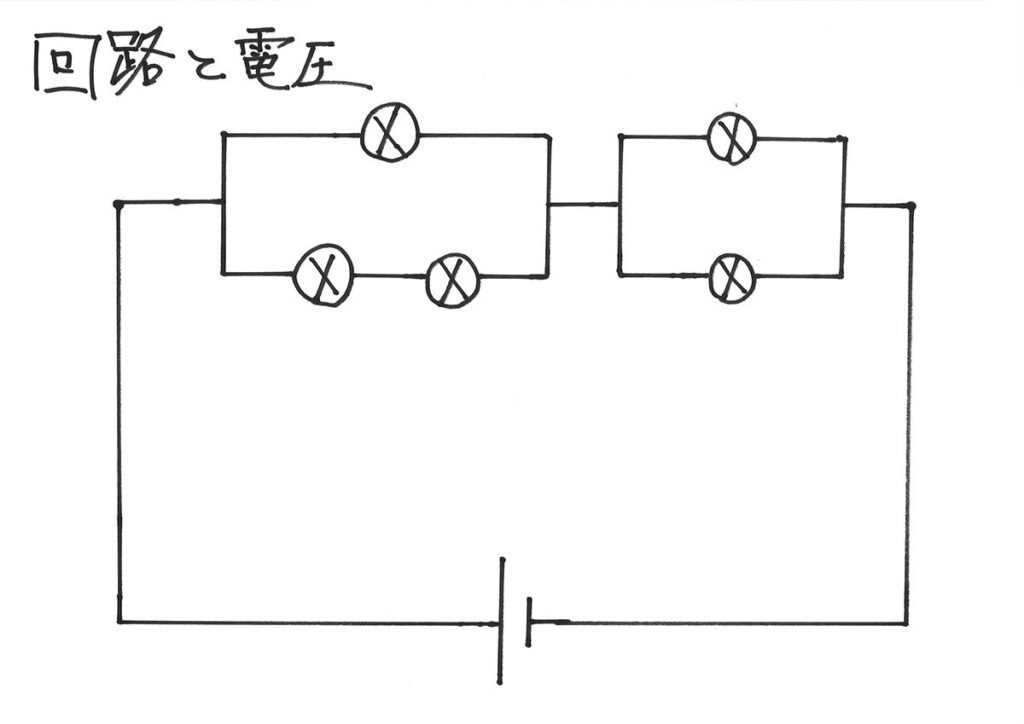
「オームの法則」をしっかり理解したので、上記のような基本的回路を考えましょう。
小学生・中学受験生の中には、上記の様な回路は、
これは、
すぐ出来るよ！
この部分の合成抵抗が〜で、
こっちの合成抵抗が〜で＿・・
とサラサラ解ける方もいらっしゃると思います。
あるいは、
「合成抵抗」って、
なんだか難しい・・・
と頭を抱えて、悩んでしまう子もいらっしゃるでしょう。
まず、「回路」という言葉が大人向けで「いかにも難しい」雰囲気です。
・電池がエイッと電圧を発生させて、電流がグルッと一周するモノ
高校物理以降の回路は、磁場なども登場して難しくなります。
まず、小学校の理科・中学受験の理科では、上記のように考えましょう。
「回路」というのは、「電流を持ち上げる電池と（豆）電球・抵抗が登場する」だけです。
そして、その結果、「グルッと電流が流れる」イメージをしっかり持ちましょう。
電気・電流に対して、
難しい・・・
出来ない・・・
と考えている方には、ぜひ出来るようになって欲しいです。
「すでにある程度分かっている」方も、「基本的イメージ」をしっかりして、応用力をつけましょう。
「合成抵抗」などの公式を、暗記していることも大事です。
さらに「なぜ、そうなるか？」をしっかり理解していると、学力が飛躍的に上がるでしょう。
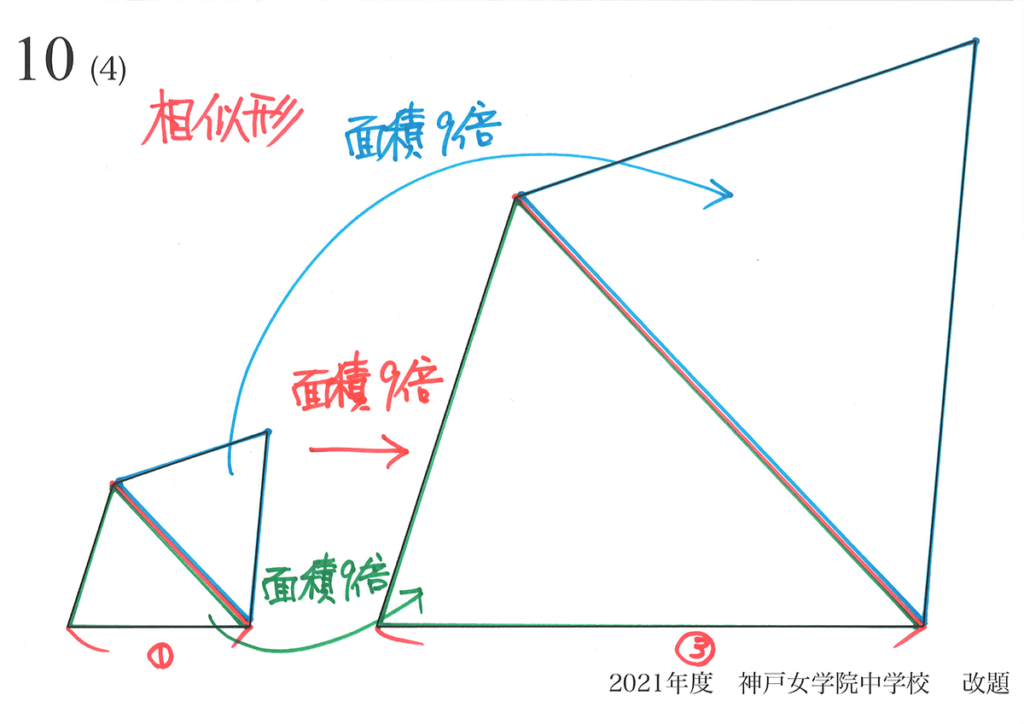
算数で「平面・相似図形の面積比」は「相似比x相似比」という公式があります。
この内容は「公式」というよりも、「原理」「事実」に近いですが、理由を理解することが大事です。
これらの「基本的公式・原理」を「丸暗記」ではなく「理解・習得する」姿勢は、学力アップの近道です。
別れて、合流する電流をイメージ
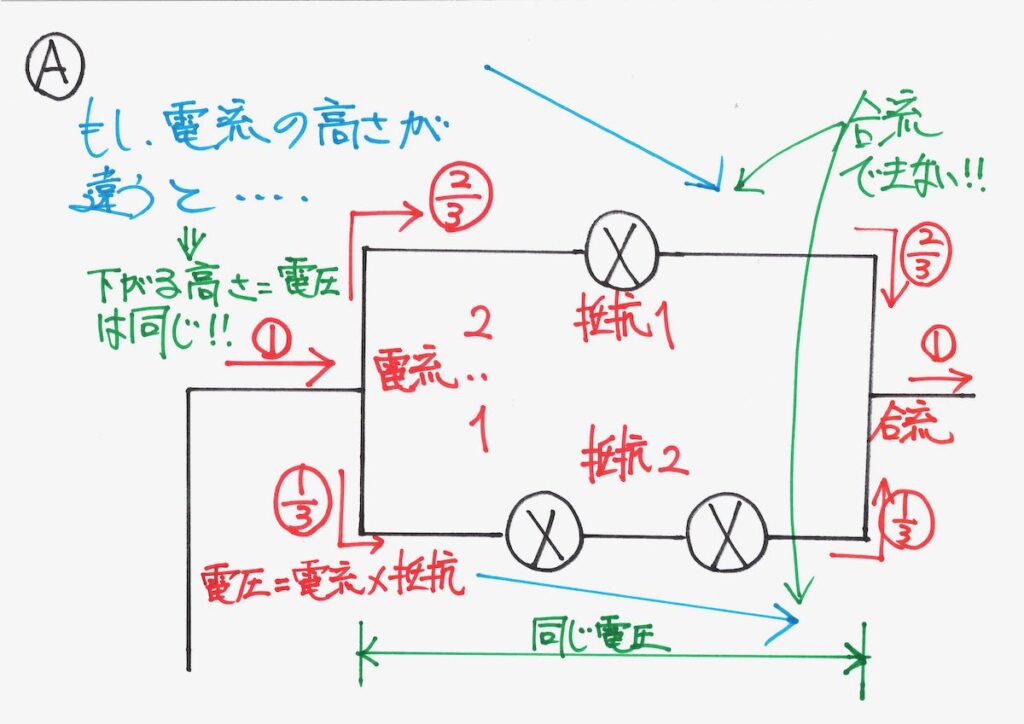
Aの部分で一度、「抵抗の大きさに反比例」して分かれた電流が、合流してBへ向かいます。
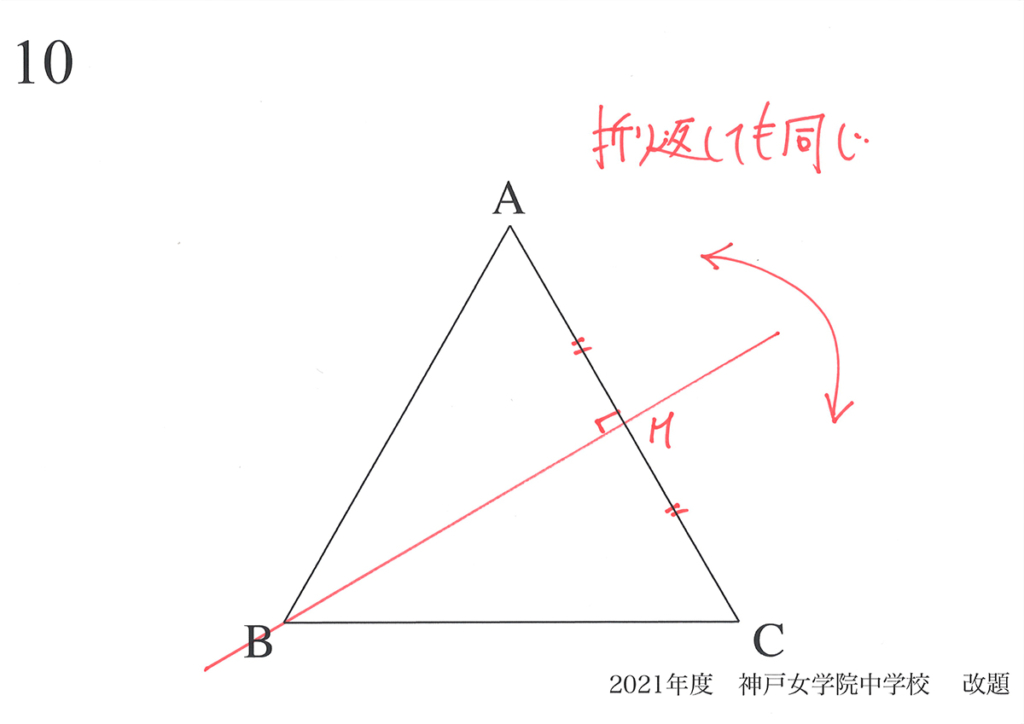
この「別れた電流の下がる高さ（電圧降下）」が「同じ」という事実を考えました。
「下がる高さ（電圧降下）」が「違う」と「合流できない」のです。
写真は、先日、東京郊外の雑木林の「自然見学会」に子どもと参加したときの光景です。
小高い山の中を散策し、山の上流から流れてくる水の流れがありました。
これらは、「川」というほどの規模ではありませんが、このように「水の流れ」をイメージしましょう。
水の流れが
合流すると・・・
水の幅・川の幅が
広がるね！
隅田川のような大きな川でなくても、小さな川やこのような水流を実際に見る経験は大事です。
このような水流を水が「チロチロと」、時には「ドドーっと流れる」様子を見る体験が大事です。
これは、写真・動画でも「見れば分かる」かも知れませんが、やはり実際に経験してほしい。
受験生は、このような時間は取れないでしょうから、上記の写真で「水の流れ」をイメージして下さい。
そして、来年見事志望校に合格して、しばらく羽を伸ばして色々遊びに行くことを楽しみにしましょう。
流れる電流を追いかけるイメージ
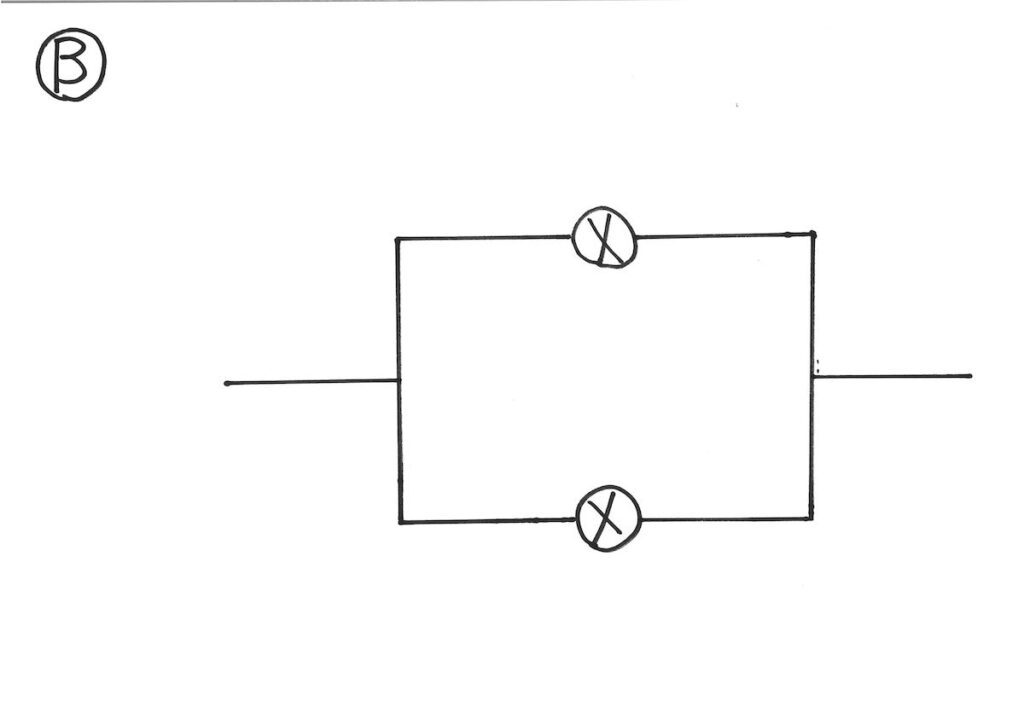
Bへ流れてくる電流をイメージして、流れる電流を追いかけてみましょう。
Aと同じように「分かれた電流の下がる高さ」は同じです。
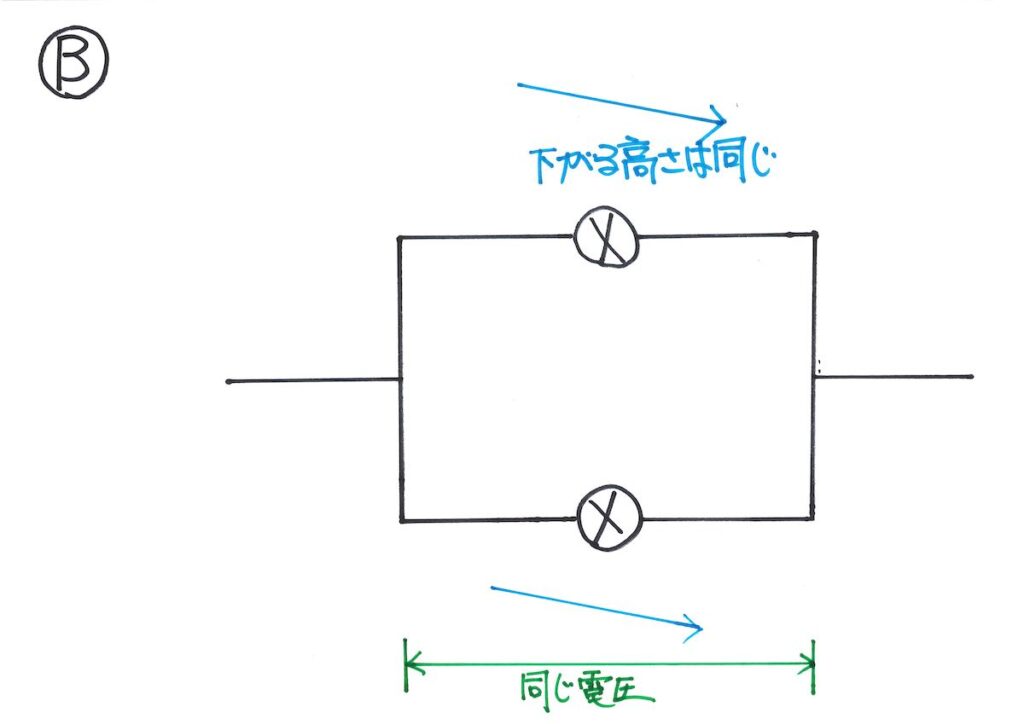
Bで「どのように電流が分かれるか」を考えてみましょう。
Aと同じように考えて、
「電流x抵抗=電圧」の「下がる電圧」が、
同じだから・・・
抵抗の比の逆数で、
電流が分かれる！
Bでは、抵抗は同じなので、電流も同じ量で分かれます。
対称性を考える
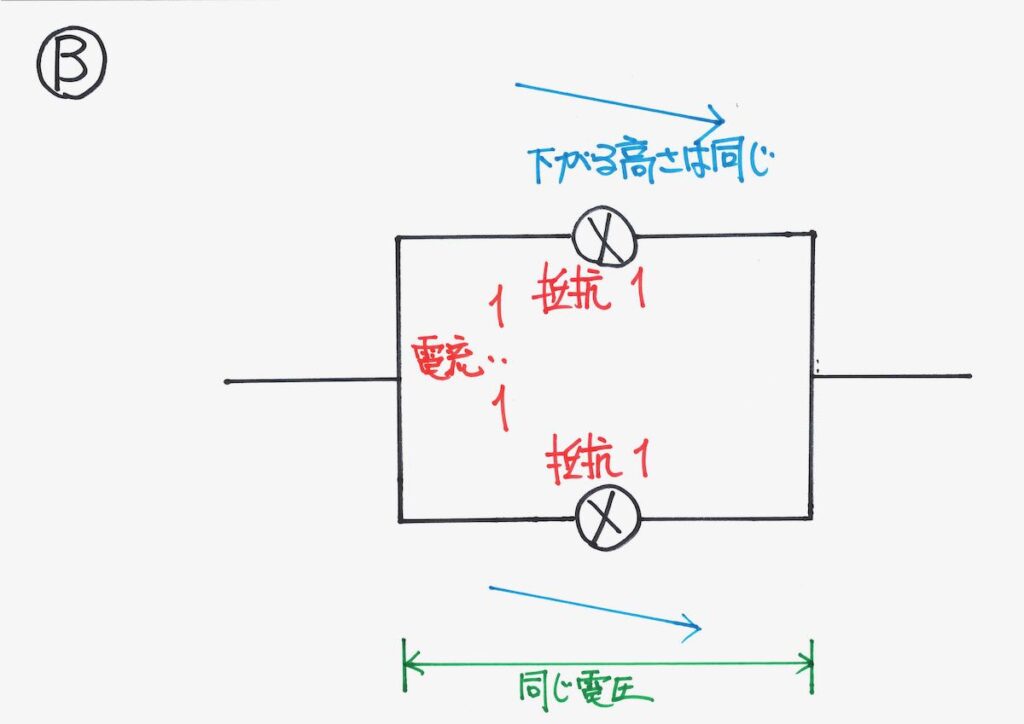
ここでは、「抵抗が 1 : 1だから」と考えても、良いでしょう。
また、「同じ=対称性がある」から「流れる電流も同じ」と考えても良いでしょう。
対称性は、算数と理科に共通する大事な性質です。
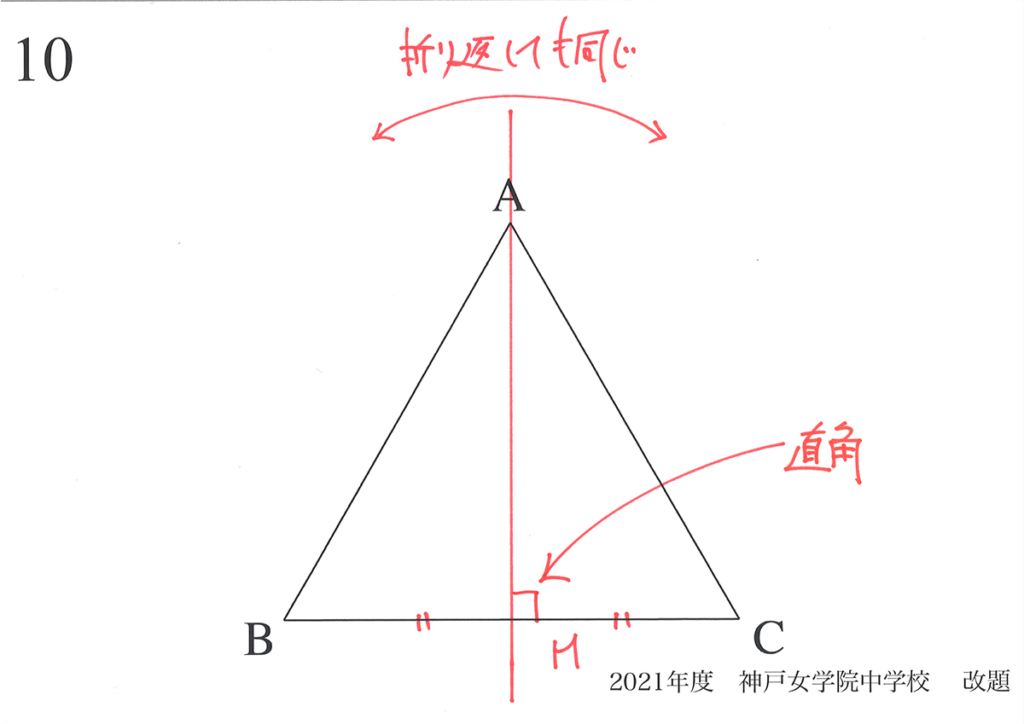
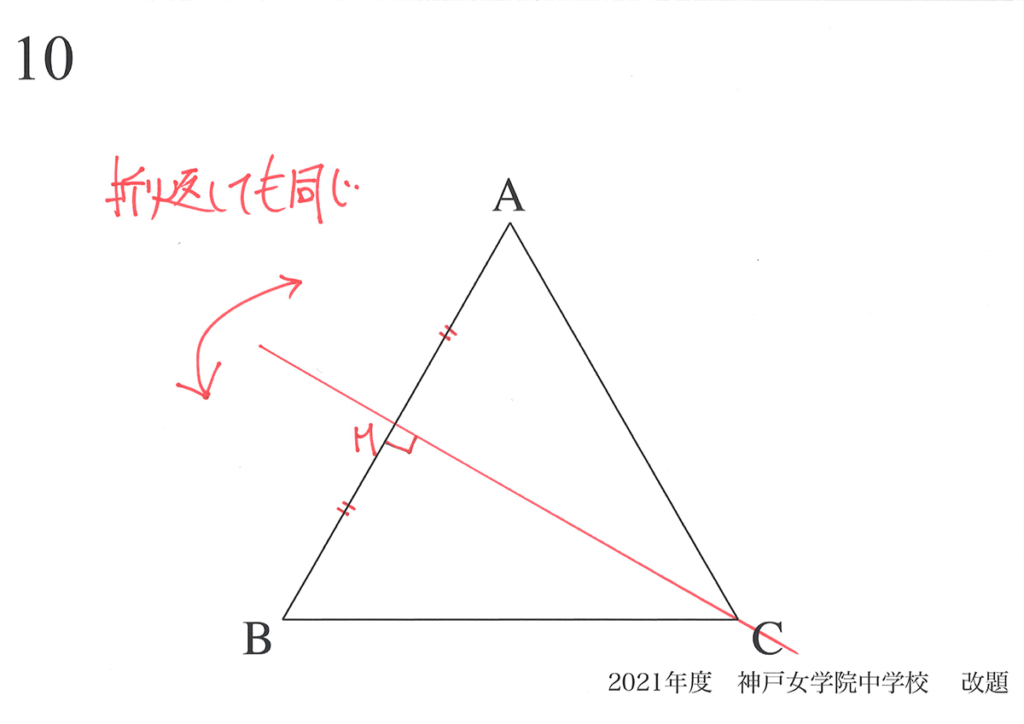
「同じ」や「対称性がある」ポイントに気づいたら、
何か
分かるはず！
と考えましょう。
回路全体を考える
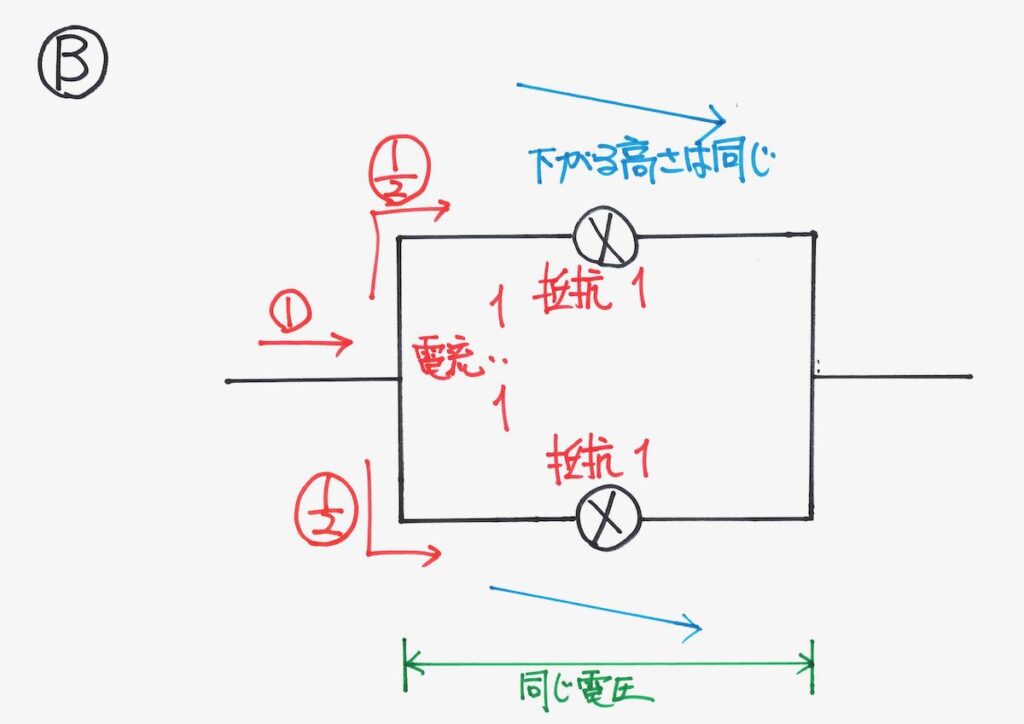
合流した電流が、同じ量で分かれます。
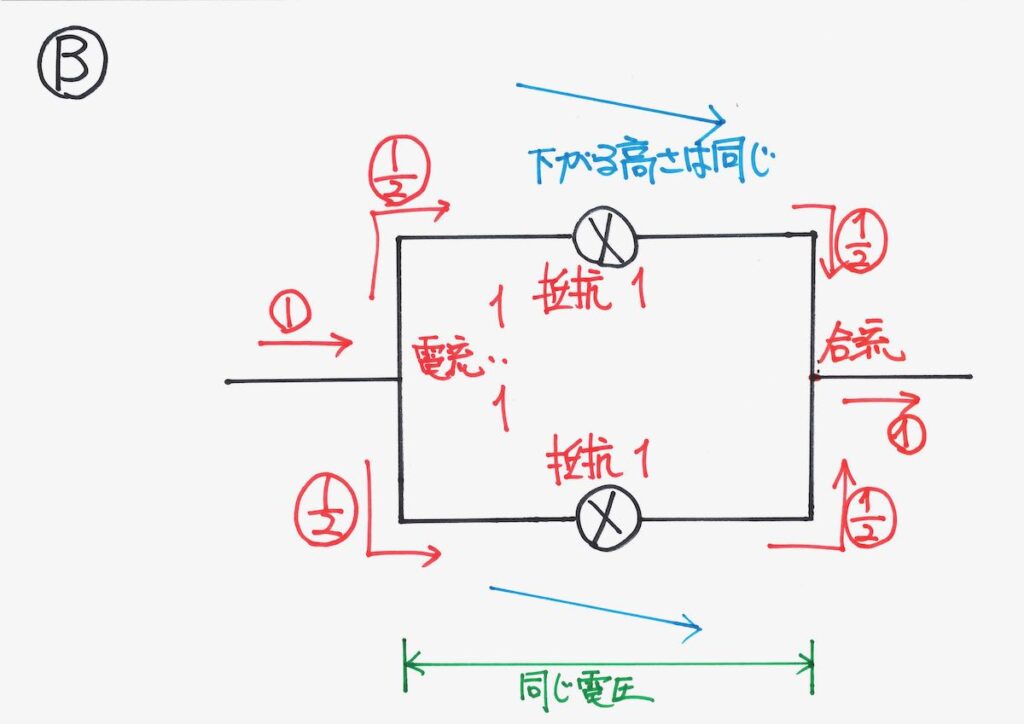
そして合流して、元の電流に戻ります。
このように、「分かれる電流」と「合流する電流」を実際に色鉛筆・マーカー等で描いてみましょう。
川の流れのように、電流が流れる現象も「自然現象の一つ」と考えましょう。
豆電球・電池・導線を用意して「人為的」に作る回路ですが、そこに電流が流れる「現象」をイメージしましょう。
A,Bで、それぞれ考えましたが、全体に戻りましょう。
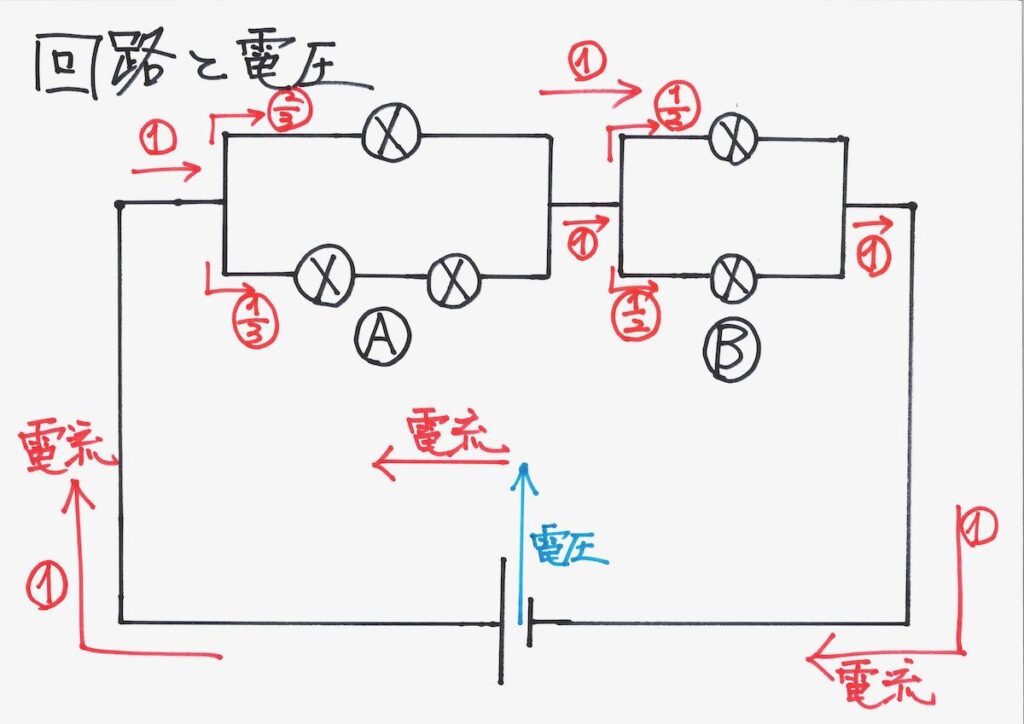
電流の流れを、全体の回路にまとめました。
「流れる電流が分かった」後は、オームの法則を考えます。
これまで、電流を考えてきましたが、電気は本質的には「電圧が主役」です。
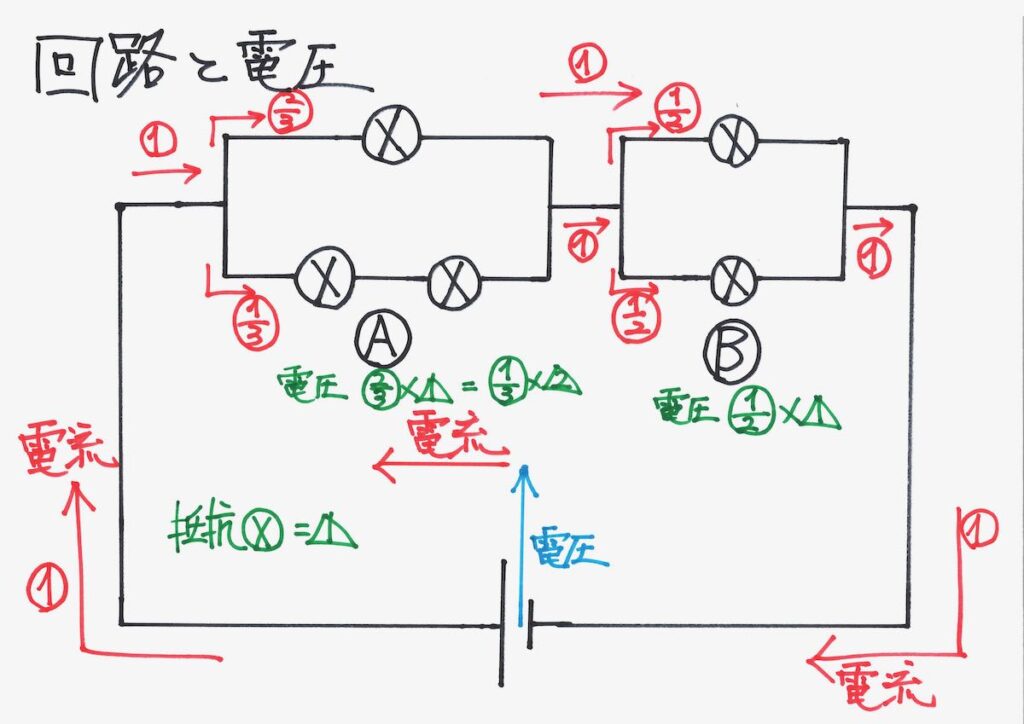
ここで、「電池が持ち上げる大きさ=電圧」と、流れる電流の関係を考えましょう。
抵抗を考えて、A,Bの電圧（降下）をそれぞれ計算しました。
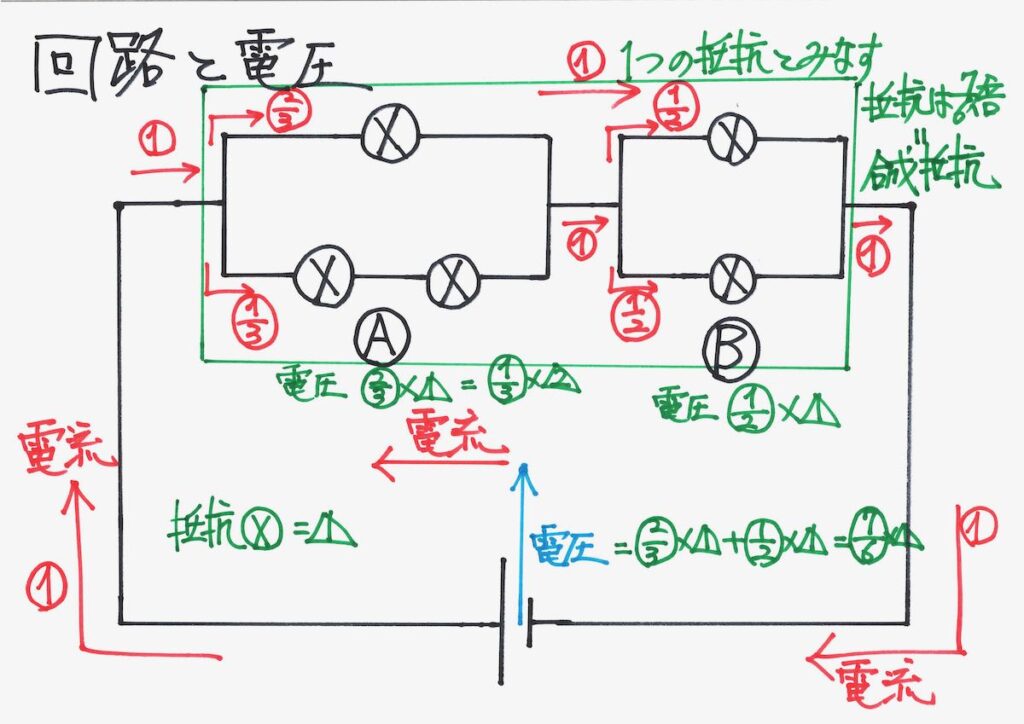
最初に、電池が「電流をエイッと持ち上げるの高さ=電圧」は、AとBの電圧降下の合計となるはずです。
AとBの電圧の比は、「2/3 : 1/2 = 4 : 3」 になります。
これで、この回路の全容が、分かりました。
これで、
流れる電流・電圧が全て分かったね。
上記のような回路を考えるときは、「合成抵抗」を考えるように教わることがあります。
そうそう。
合成抵抗を考えると早いよ・・・
でも、電流と電圧を考えると
分かりやすい。
様々な回路の問題も、このように考えると電流・電圧の全てが分かります。
確かにそう！
全部分かるのは、嬉しい。
慣れると、上のような考え方も「素早く」出来るようになります。
そして、「回路の全容が分かる」意味では、このような「基本を考える」姿勢を大事にして欲しいです。
試験などでは「合成抵抗」を考えた方が、早く解けるので、「公式の内容を理解する」ようにしましょう。
次回は、合成抵抗を考えます。
次回は下記リンクです。
