前回は「回路のわかりやすい考え方・解き方 1〜電圧と電流と抵抗・「電圧が主役」のオームの法則・閉じた回路・分かれる電流と合流する電流・回路全体を描いて理解力アップ〜」の話でした。
電流と電圧と抵抗が登場する回路：電流の流れと高さ
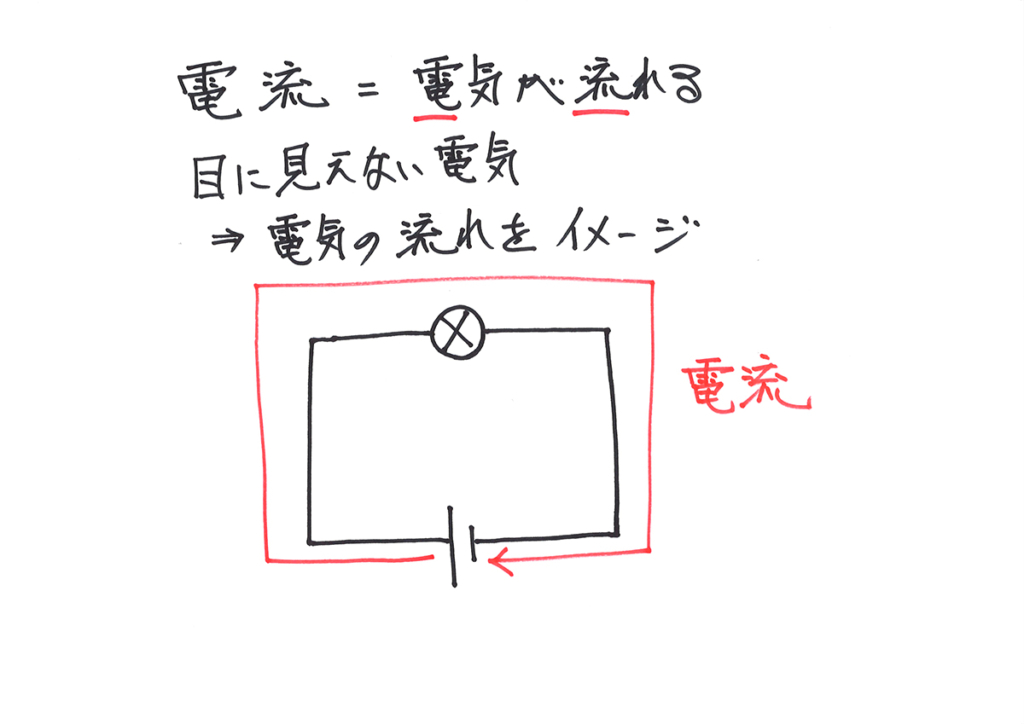
電気を学び始めると、電流・電圧・抵抗の三つが登場します。
そして、上のような「電池一つ、（豆）電球一つ」の非常に基本的な回路が登場します。
そして「オームの法則」という法則・公式を習って、ここからが基本から応用になって行きます。
少しずつ複雑な回路を勉強して、電池や電球が直流・並列など、様々な回路があります。
男子小学生基本的な回路は
分かるけど・・・
男子小学生少し変わった回路が
登場すると、分からなくなる・・・
応用問題が難しく感じられ、「苦手分野」になりやすいのが電気。
そもそも、「回路」という言葉が馴染みがなくて、「難しそう」なイメージです。
「ばね・てこ」や「かっ車」など、イメージしやすいモノに対して、難しそうな「回路」という言葉。
「回路」というと半導体や最新電気機器などが思い浮かび、難しい感じです。
・エネルギー・物質などが発生し、再び元の場所に戻る道筋・経路
・物理：電流・素子が導体（電線・電熱線）によって環状（一周する形）に繋げられたもの
「回路」の定義（決まりごと）とは、上記の通り「電流などが、一周して戻ってくる経路」のことです。
男子小学生「再び元の場所に
戻る道筋・経路」・・・
女子小学生やっぱり
難しい感じがする・・・
あまり難しく考えず、下記のように考えましょう。
・電池がエイッと電圧を発生させて、電流がグルッと一周するモノ
男子小学生「エイッと、グルッと」だね。
なんか分かった気がする・・・
このようなイメージを持って、「回路」を難しく考えずに、しっかりイメージしましょう。
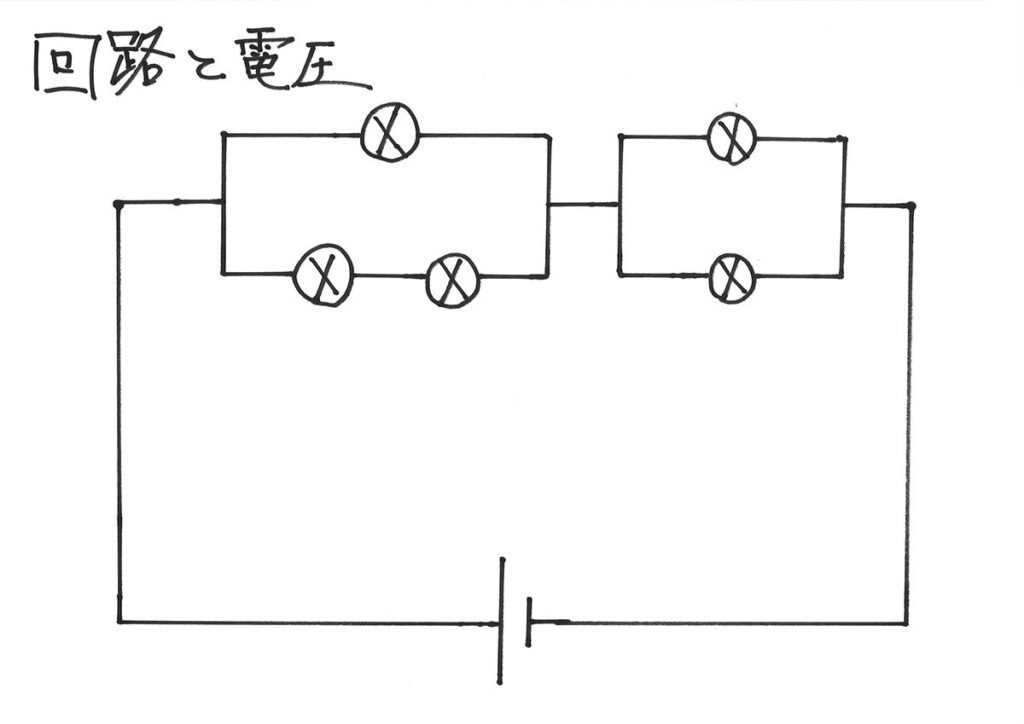
電池一つに、並列の電球が二つ直列に並んでいる「基本的回路」を考えます。
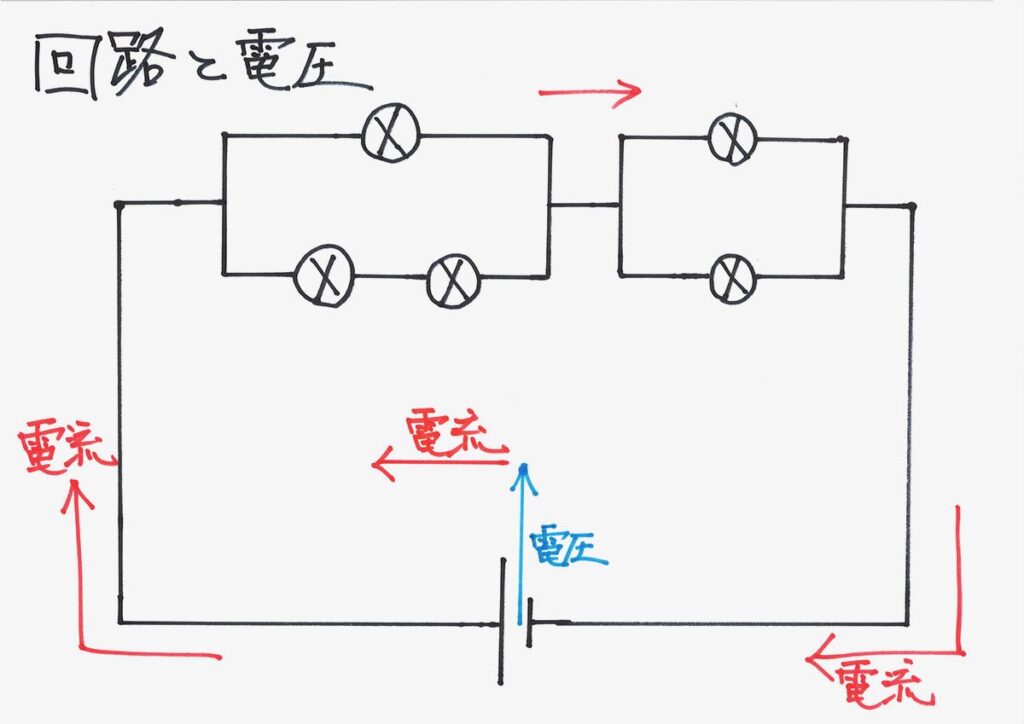
「回路」とは「電池がエイッと、電流がグルッと」です。
この「電池がエイッと、電流がグルッと」をイメージするために、色鉛筆等で描いて下さい。
すると、難しく感じる「回路」が分かりやすくなるでしょう。
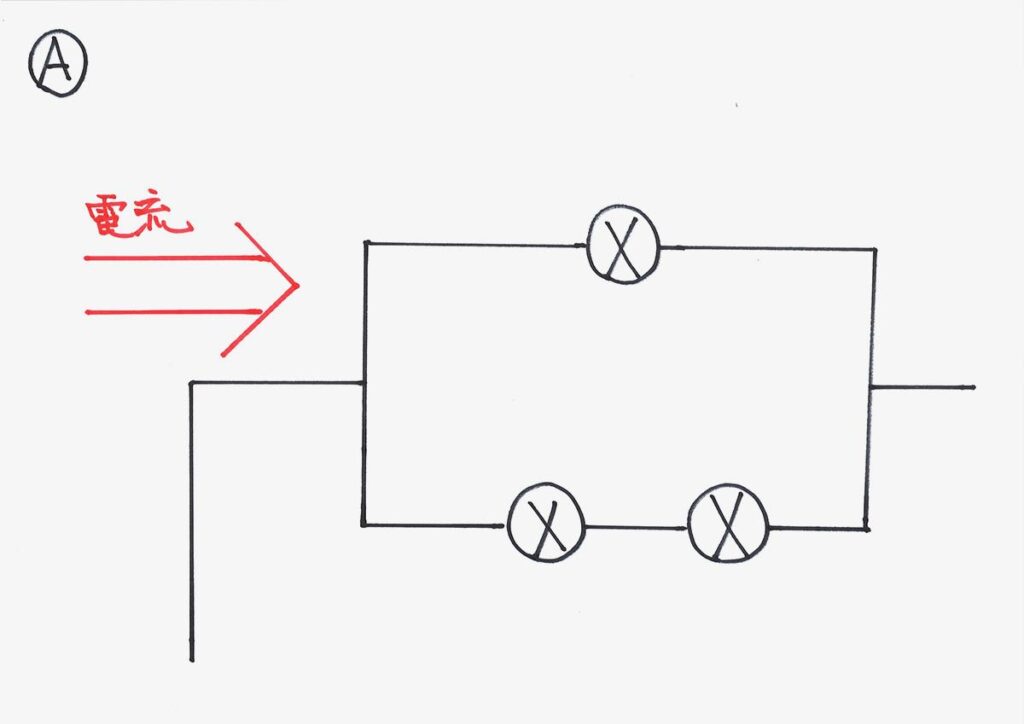
Aの「電球1つと直列電球2つが並列」の回路の部分を考えましょう。
慣れると難しくないですが、「電球1つと直列電球2つが並列」と言われると、
男子小学生直列と並列が
両方で難しい・・・
難しく感じる時は、「電流の流れ・高さ」をイメージしましょう。
電球1個、電球2個の部分に電流が分かれます。
「川の流れ」のイメージで、「幅が広い川が幅が狭い川に分かれる」イメージです。
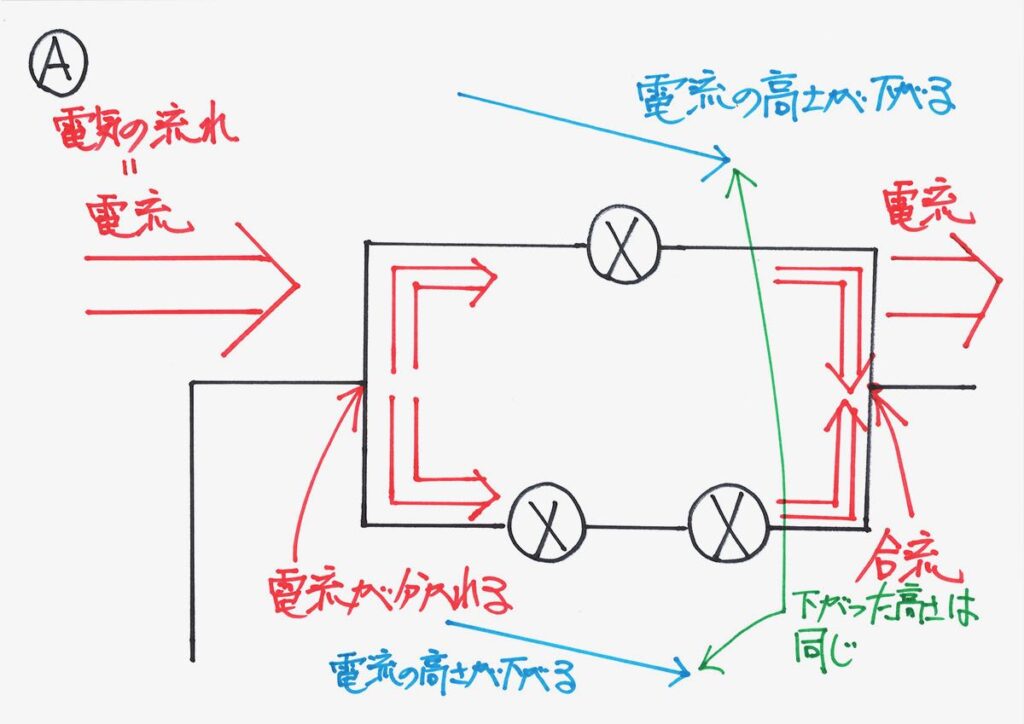
二つの流れに「分かれた」電流は、また合流します。
塾講師下がる高さ（電圧）は
同じだよ！
「下がる電圧の大きさは同じ」と習います。
この「下がる高さ（電圧）が同じ」の理由を考えてみましょう。
男子小学生なぜって・・・
これも「暗記」じゃないの？
女子小学生覚えれば良いと
思っていたけど・・・
回路で「分かれた電流の下がる高さが同じでなかったら」どうなるか、考えてみましょう。
「同じ」ではなく「違う」時のイメージ
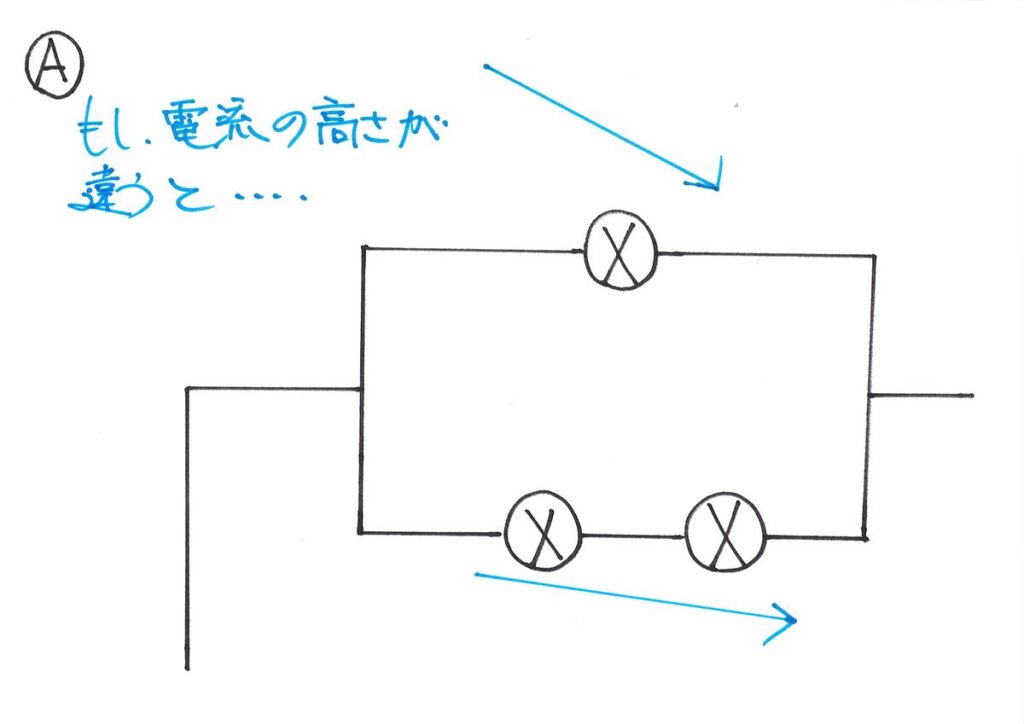
「下がる高さが違ったら」などを考えるときは、頭で考えても良いですが、描いてみましょう。
そして、「違うとき」「小さく違う」ではなく「大きく違う」イメージを描きましょう。
少し、誇張するくらいでも良いでしょう。
男子小学生えっ！
勝手に「大きく」してもいいの？
「違う量・大きさ」が、大事な条件であれば、その条件に合わせます。
条件がなければ、自由に考えてみましょう。
女子小学生確かに、大きく違う風に描いた方が、
分かりやすいかも・・・
「描くこと」を難しく考えないようにしましょう。（上記リンク）
上の図では、僕が定規を使って描いていますが、定規を使わないでも良いでしょう。
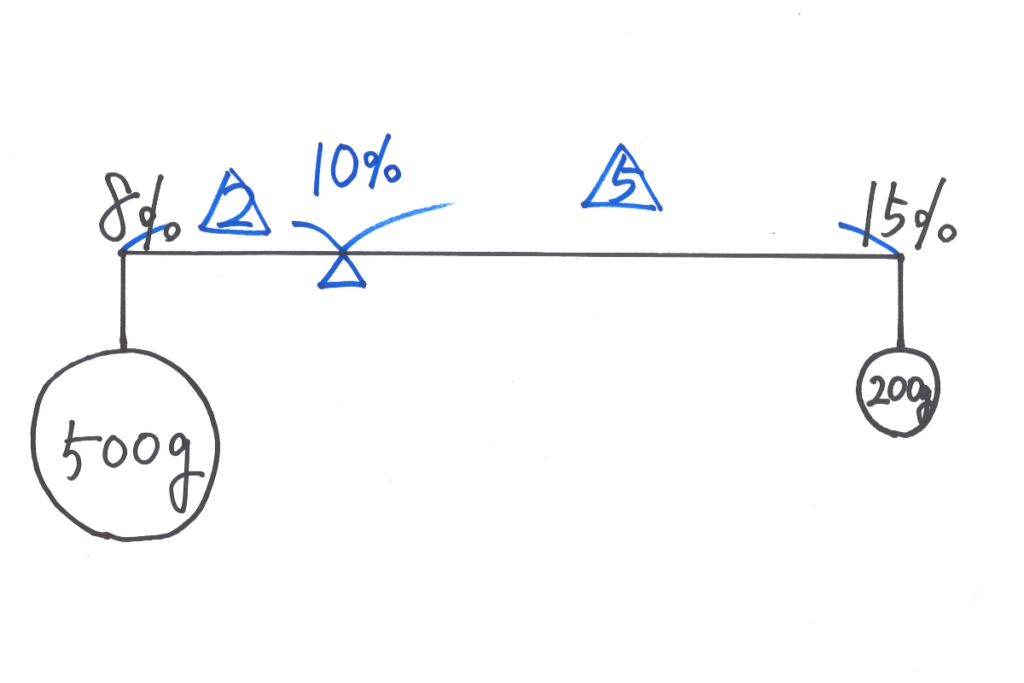
例えば、てんびん算をご紹介した話では、てんびんのおもりを少し大きめに描いても良いです。
上のてんびんの「500g」と「200g」のおもりは、重さが「5 : 2 」で、直径も「5 : 2 」で描いています。
それぞれの「おもり」の密度によりますが、「同じ密度」であると仮定します。
その場合、「おもりの重さ」は「球の体積に比例」するはずです。
すると、直径が「5 : 2 」の球の体積比は、「5x5x5 : 2x2x2 = 125 : 8」となってしまい、全く異なります。
本来、算数や理科では、スケール感・バランスは非常に大事です。
本来ならば、上の図の「おもりの大きさ・直径の違い」は、もう少し近くなります。
「てんびん算」は、「おもりx長さ=回転する力（モーメント）」が「釣り合うイメージ」が大事です。
そこで、重い方の「おもり」を少し誇張してました。
そして、「釣り合う」イメージを思い浮かべる話をご紹介しました。
「しっかりしたイメージを持って、スケール感・バランスもしっかり」が最も良いでしょう。
実際に色々と描いてみて、自分なりに出来るようになりましょう。
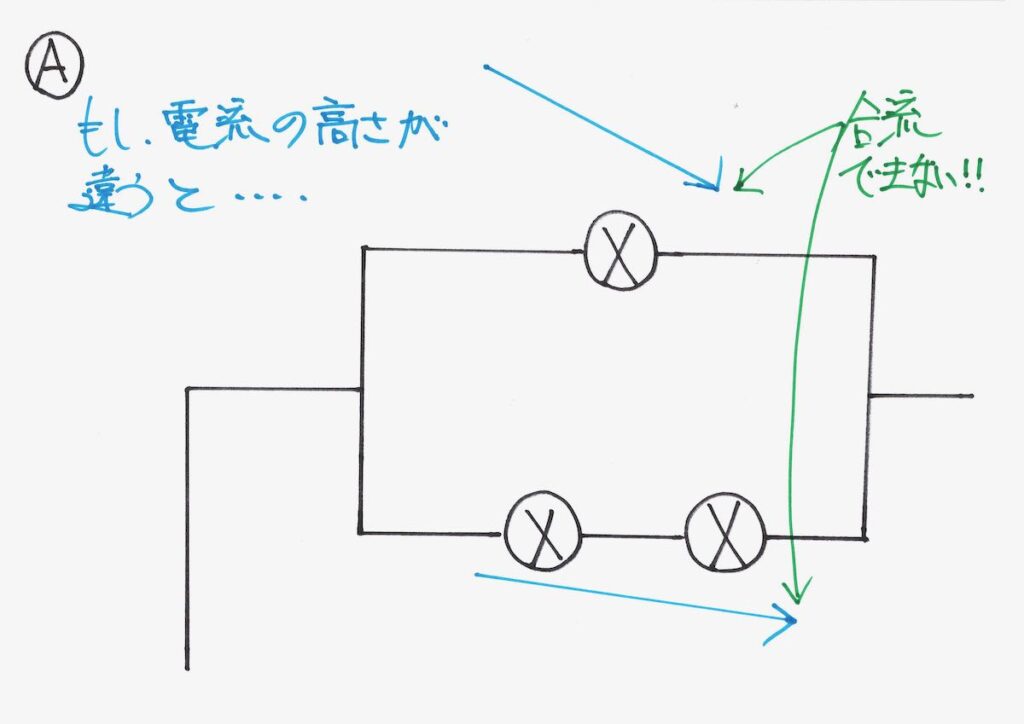
「違ったらどうなるか？」と考えることは非常に本質的で、理科の大事なポイントです。
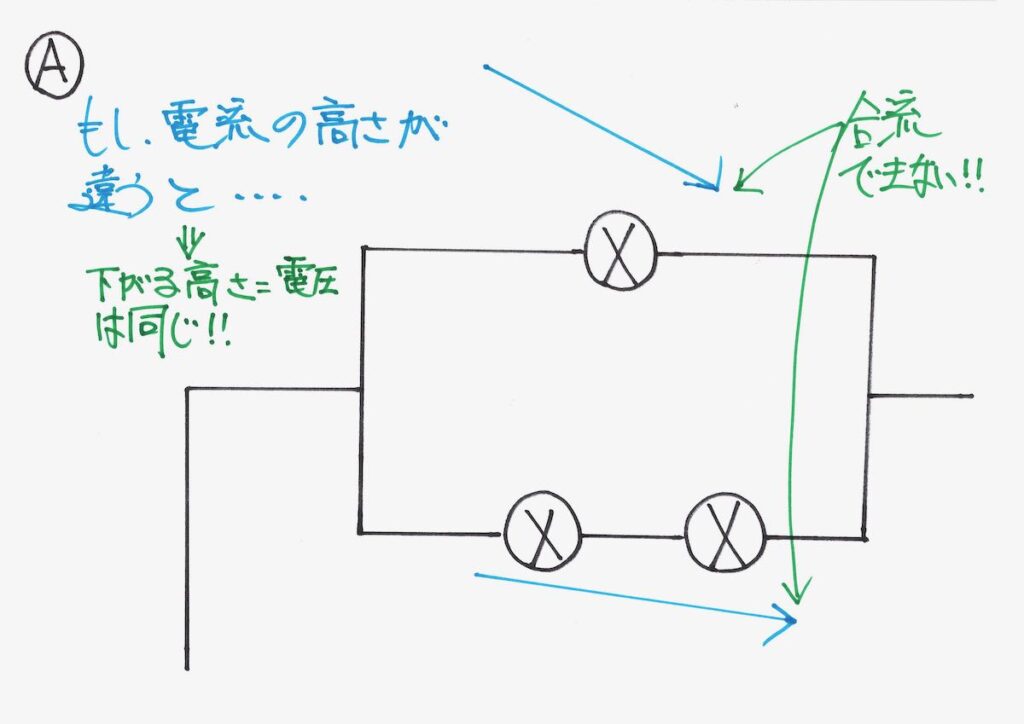
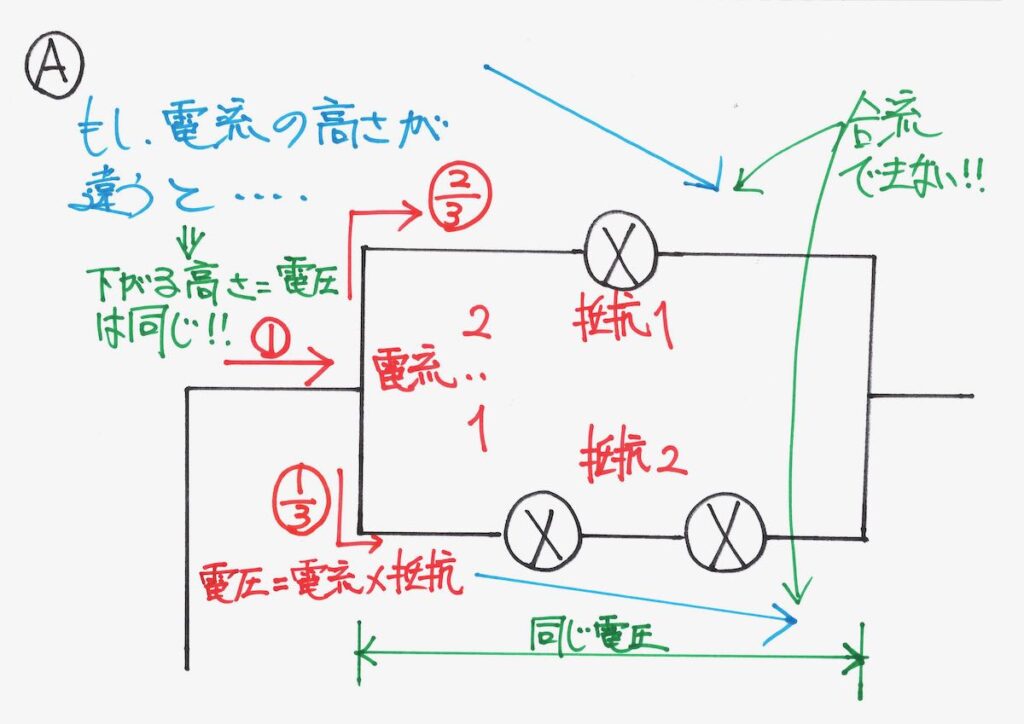
例えば、Aの上の電流の方がグッと大きく下がると、どうなるでしょうか。
「分かれた電流」が「合流できない」状態になります。
男子小学生これは
困るかも・・・
女子小学生合流できなかったら、
電流はどうなってしまうのかな・・・
分かれた電流が「合流できない」事態は、おかしいです。
「合流できなかった」場合、電流が一周できないので「回路にならない」のです。
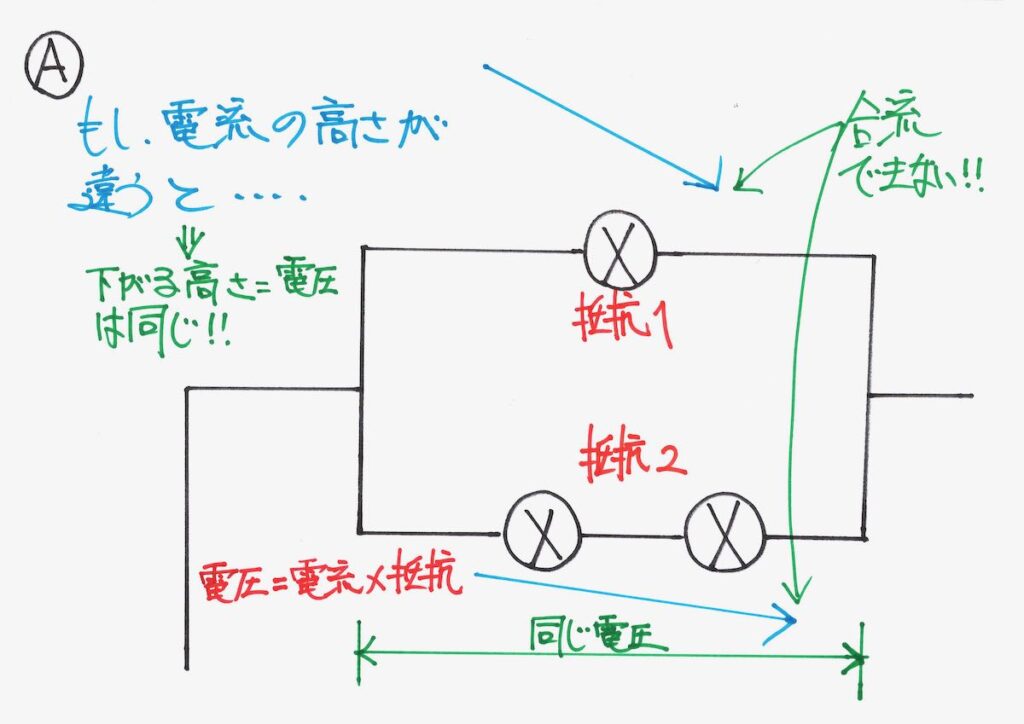
そこで、分かれた両方の線で「電流が下がる高さ=電圧」は同じです。
すると、「電流が合流できて、合流した電流が流れ続ける」回路になります。
「電流は抵抗の逆比」を理解して学力アップ
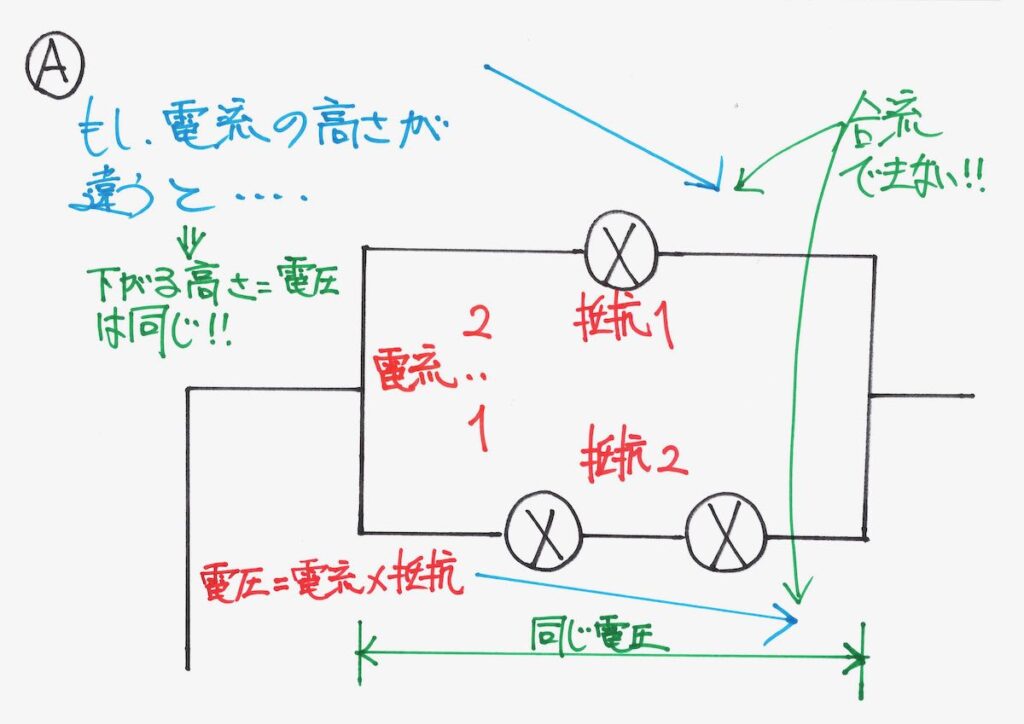
そして、オームの法則「電圧 = 電流 x 抵抗」を考えましょう。
上の線は抵抗=1、下の線は抵抗=2なので、「抵抗の比は 1 : 2」です。
「抵抗が2つ直列」は、流れる抵抗が「ガンガンと」続けて抵抗を受けるイメージです。（上記リンク）
「掛けて同じ」だから、「電流の比は、抵抗の逆比」になります。
「掛けて同じ」だから、「電流の比は2 : 1」です。
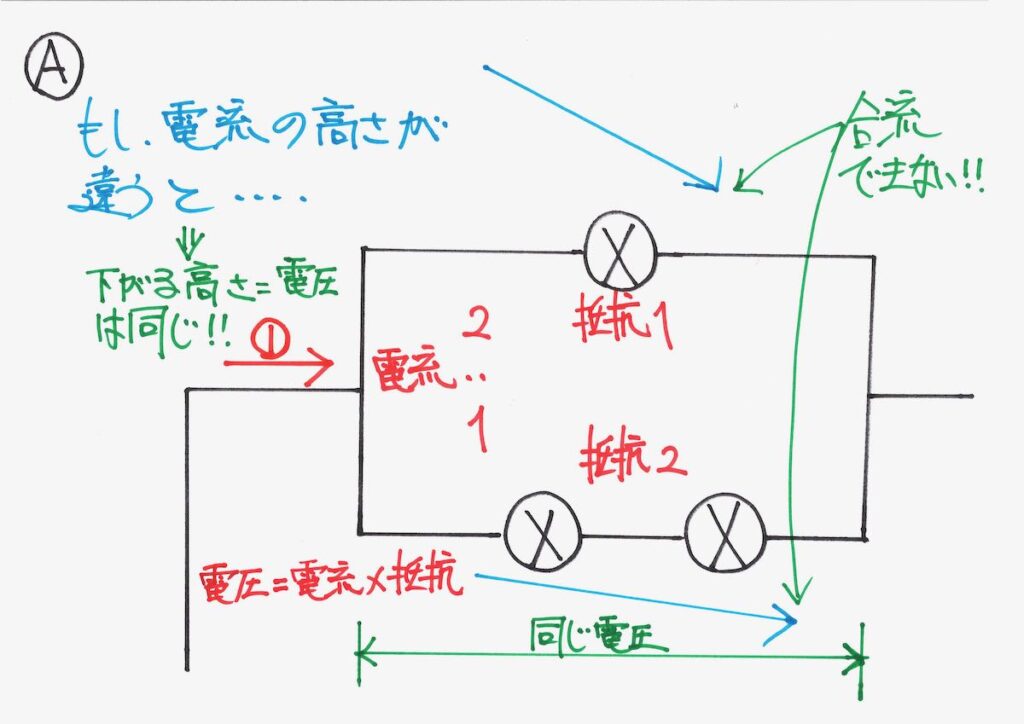
①の大きさの電流が流れてくるイメージを考えましょう。
そして、2 : 1で、電流が分かれます。
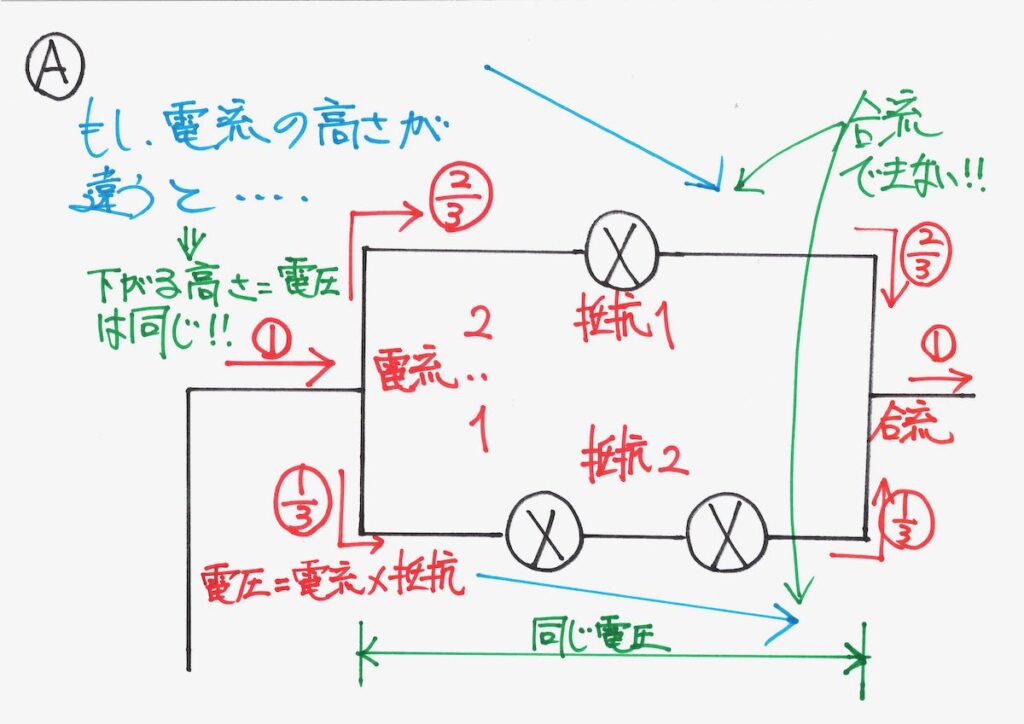
回路Aの出口で再び合流して、元の電流になります。
男子小学生確かに、電流を
描くと分かりやすいね・・・
女子小学生「電流の比は、抵抗の逆比」と
暗記していたけど・・・
女子小学生この様に考えると、
自然と頭に入る！
この様に「基本・原理をしっかり理解」すると、回路が複雑になっても出来る様になるでしょう。
続いて、合流した電流が「回路B」に向かいます。
BはAより分かりやすいですが、同じように電流を描いて、流れる様子をイメージしてみましょう。
次回は下記リンクです。
