前回は「算数のおすすめ勉強法〜難関校志望者向け・一題一題しっかりと理解する姿勢・状況を整理=ポイントを整理・自分の手で考え方を再現・メモ書き・未知数を色々考える・自分の考えやすい方法〜」の話でした。
算数を得点源や武器に
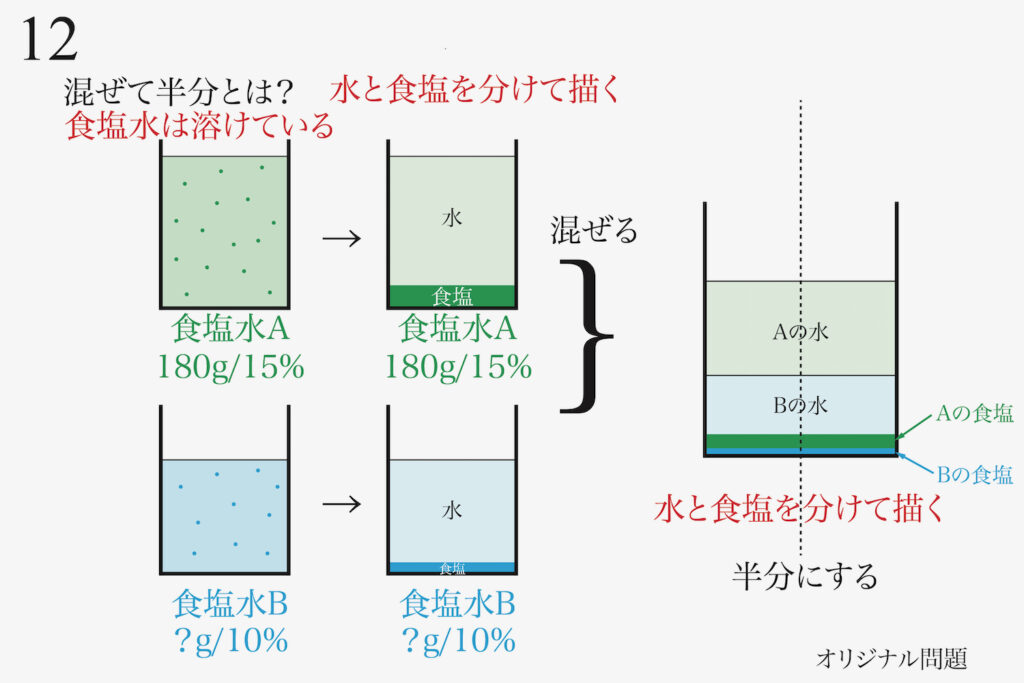
中堅校・難関校志望者の方向けに、算数の学力が上がる学び方をご紹介しました。
今回は、最難関校志望者向けの算数の効果的学び方です。
基本的な方針は同じで、「分かったつもり」にならないで、しっかり手を動かして理解することです。
最難関校志望者は、各分野ある程度できると思います。
男子小学生ちょっと
苦手分野があって・・・
「苦手分野」がある方がいると思いますが、早めに苦手分野は出来るだけ克服しましょう。
「得意科目・得意分野を意識して、自信をもつ」ことは非常に大事です。
難しい問題に取り組まなければならない、最難関校志望者の方は、
男子小学生僕は、ニュートン算や旅人算などは
大体できる！
女子小学生私は、整数問題や図形問題は
とっても得意！
得意分野をより強く意識して、それらを武器にして算数での突破力を養成するのが大事です。
どの学校においても、最重要科目である算数。
特に最難関においては、「算数で他の受験生に大きく差をつけられる」状況は避けなければなりません。
中堅校〜難関校までであれば、「算数の失点を他の科目でカバー」できる可能性があります。
一方で、「すべての科目であるレベルに達している」方ばかりが受験する最難関校です。
算数での差を「他の科目でカバー」は、非常に難しいです。
そのため、最難関校志望者の方には、ぜひ算数は得点源にして欲しいと思います。
男子小学生算数よりも、社会や国語の方が
得意だよ。
男子小学生僕は、模試で算数はまあまあの
成績だけど、得点源は無理そうかな・・・
各科目の中でも、算数は「直前まで伸びる」傾向が強いので、一生懸命学んで見ましょう。
難しい良い問題を繰り返し解く
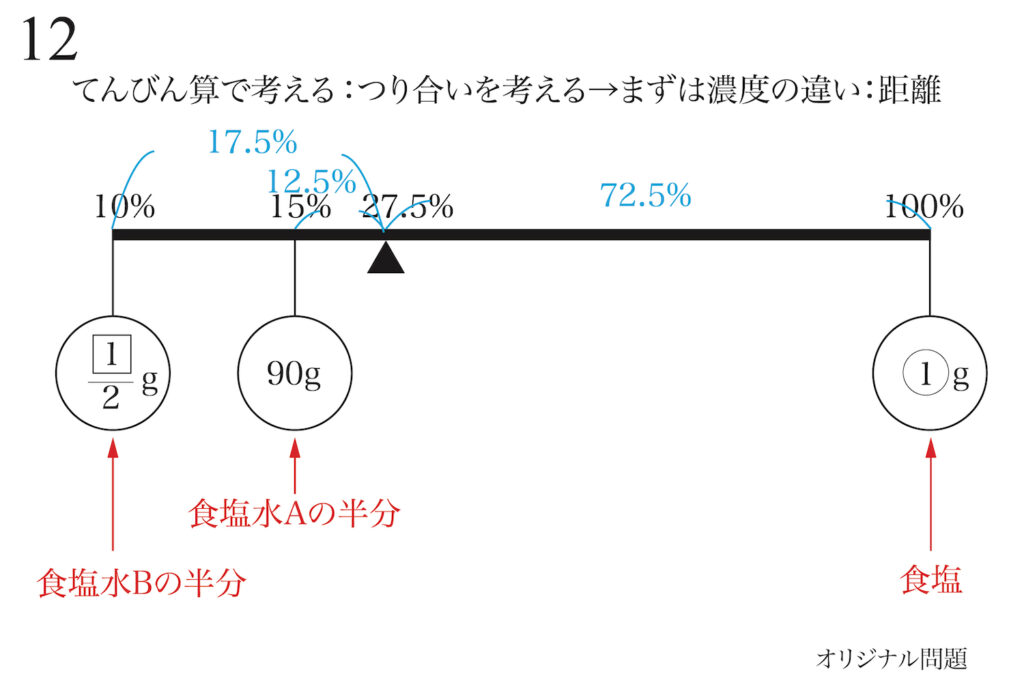
算数は、直前期に学力が急上昇する可能性があります。
男子小学生「算数は直前期に上がる」は、
聞いたことあるけど・・・
女子小学生それって
本当なの？
どの学校志望者の方、他の科目でも起きうるのが「秋以降の成績急上昇」です。
実は「最難関校の算数」において、最も「成績急上昇」の可能性があります。
男子小学生それは
なぜ？
最難関校の算数は、「複数の分野にまたがる考え方」で解く問題が多いです。
これは、中堅校〜難関校の算数とは、大きく違う特色です。
図形問題は、いわゆる「平行・相似」などの「図形的考え」のみで解ける問題が多いです。
一方で、様々な所見の状況を考える問題などは、「複合的問題」が多いです。
女子小学生整数問題の考え方と棒グラフとか
面積算を合わせた問題とかあるね・・・
「様々な分野が複合」する問題が多い「最難関校の算数」は、応用力が大事です。
そのため、各分野の理解が進むと一気に学力が上がる傾向があります。
一方で、「スランプに陥りやすい」傾向が強いのも「最難関校の算数」です。
「様々な分野・考え方が複合」しているので、時々「不調に陥る」可能性があります。
「不調になった時」は、基本に立ち戻って「しっかり理解」を、もう一度やってみましょう。
そして、「最難関校の算数」向けの勉強では、「難しい良い問題」を繰り返し解くのが効果的です。
何度もやって「覚えてしまう」くらい、取り組む問題があると良いでしょう。
すると、また少しずつ成績が上がり、ある時に色々な発想が身につくでしょう。
男子小学生解法を丸暗記
すれば良いの？
ここで、「覚えようとする」のと「覚えてしまう」のは、全然違います。
何度も何度も同じ問題をやってみて、その思考プロセスを習得して「覚えてしまう」感じです。
女子小学生「覚える」のではなく、
「覚えてしまう」が良いんだね・・・
すると、「複合問題への考え方」が一つしっかりと身について、応用力が大きく上がるでしょう。
・「難しい良い問題」を繰り返し解く：「覚えてしまう」くらい
・「複合問題への考え方」を一つ一つしっかり身につける
最難関校・算数の学力アップ勉強法：採点者の目を意識
今回は「最難関校合格へ向けて」具体的な話です。
プロセスを、最難関校受験生向けに少し変更しています。
1.問題に挑戦！ しばらく考える（出来たらOK）
2.「なぜこのような考え方をするのか」や異なる解法も考えながら、図を描いたりメモしながら解答を読む
3.解答を閉じて、再度挑戦！ 出来なければ、2をもう一度
1,2が少し異なり、最難関校受験生は「自分なりに理解して」メモすると良いでしょう。
男子小学生こうしたら、
解けないかな？
女子小学生こう考えたら、
どうかな？
色々考えながら、解答を読み進めるのが良いでしょう。
ある程度学力が向上し、問題数もこなした夏休み以降は、
男子小学生こうしたら、
どうかな？
自分なりに色々と考えてみましょう。
それまで培ってきた実力が頭脳の中で統合され、相乗効果を産むでしょう。
図形問題は「解答と異なる補助線」をちょっと引いてみて、
男子小学生どうかな？
上手くゆくかな？
女子小学生この補助線では
解けないかな？
少し「自分なりに考えてみる」ことは思考力を磨きます。
補助線が良くなくて解答に到らなくても、「上手くない補助線を引いてみる」経験は大事です。
本試験の試験場で、
女子小学生これは
いい補助線かな？
女子小学生これは上手くないかな？
ちょっと違いそう・・・
早めに気付けるようになります。
こういう補助線にはコツ・ポイントがあり、それを教わるのも良いでしょう。
実際には、「自分でやってみて勘を磨く」のが、遠回りのようで最も近道です。（上記リンク）
3は記述式試験を想定して「実際に解答を作る」感じで紙に書くのが望ましいでしょう。
答案は「他人である採点者が見て、採点する」事を意識しましょう。
これは「簡単そうで難しいこと」です。
「他者の目を意識する」のは、大人でも難しいことです。
そこで、無理に「採点者の目を意識」しなくても良いでしょう。
男子小学生採点者、学校の数学の先生の
目を意識するのは、難しいよ・・・
あまり難しく考えず、「答案は自分ではなく、他の人が採点する」ことを少し考えましょう。
すると、記述式の答案などで「どのように書くか」が意識され、より良くなるでしょう。
そして、「自分が何を考えているのか」を明確に表現できるようにしましょう。
「同じような発想」で考える：解答以外の解き方にトライ
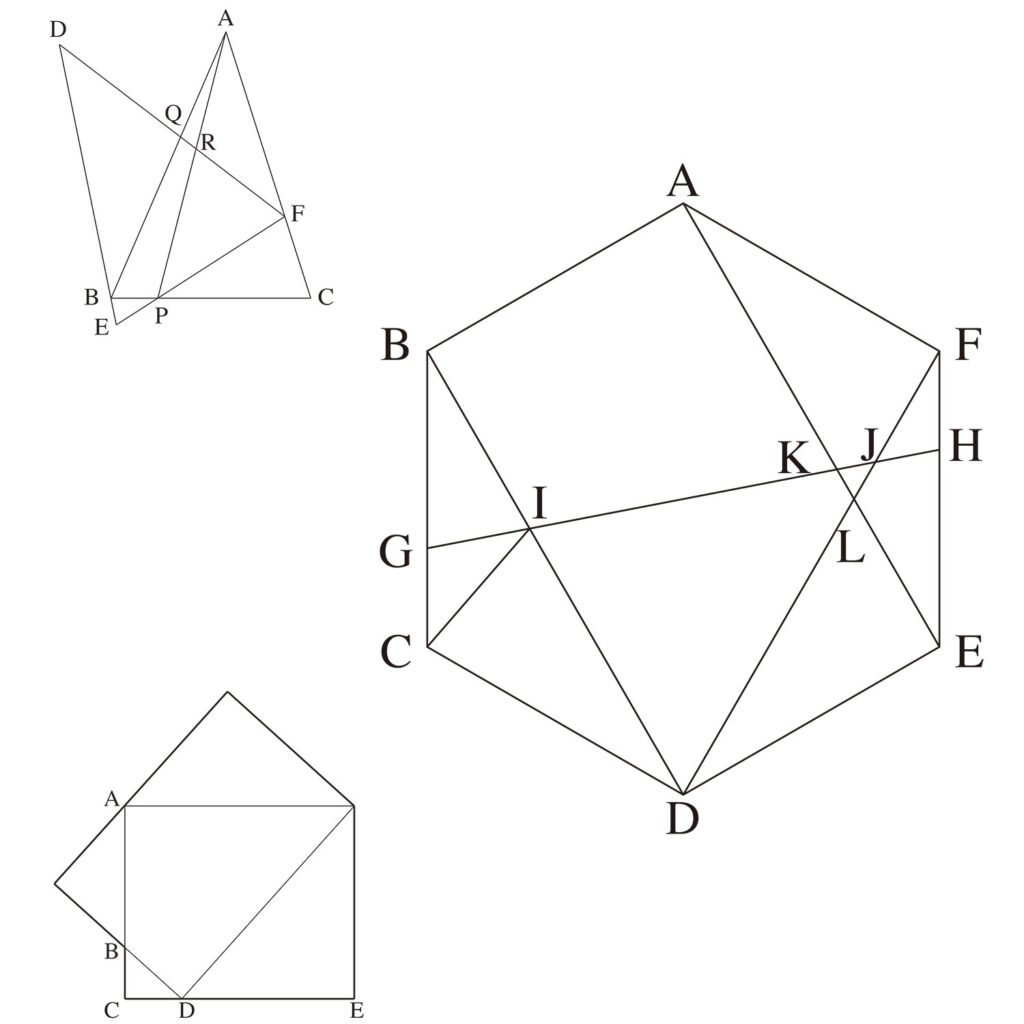
問題2の解法Bで、問題の図形の外に三角形を作成する解法を、上記リンクでご説明しました。
こでは、「与えられた図形の外に飛び出す」ことが最大のポイントです。
いわば「自分で世界を広げる」イメージです。
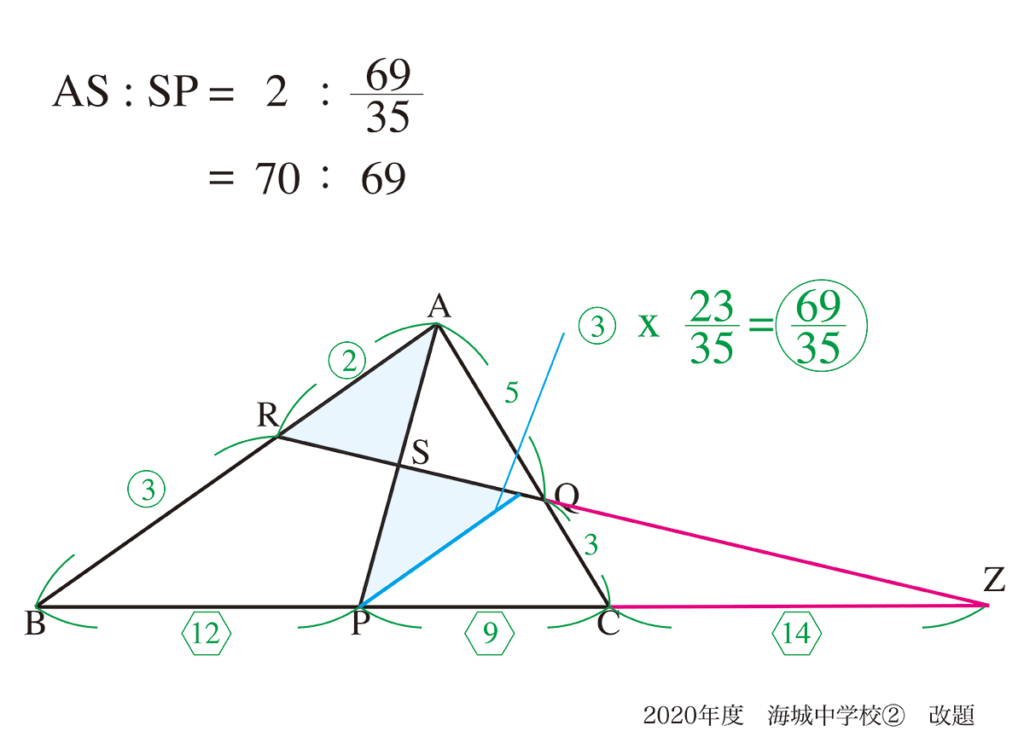
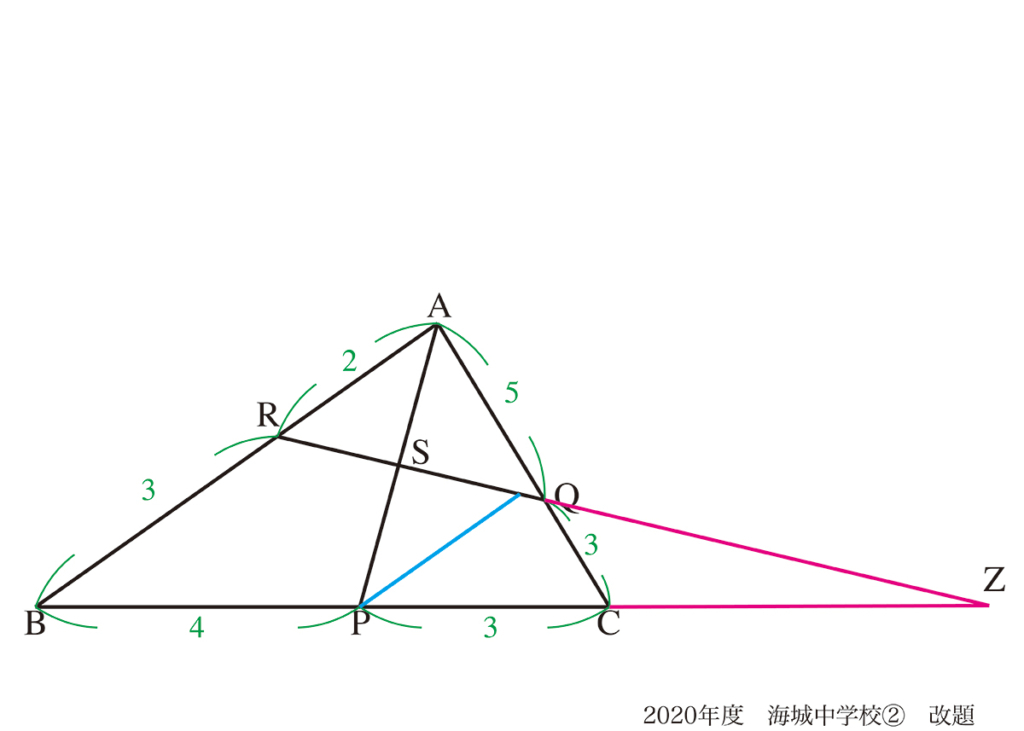
上図のように三角形を「外側に」作る解法は、別の方法も考えられます。
解答に記載されていなくても、「同じような発想」で図形問題の解答に取り組んでみましょう。
そして、解答に至る努力をしてみましょう。
「同様な考え方」であっても、異なる補助線を考えて、問題を解き進めることは非常に良い姿勢です。
「図形の本質」を考えながら解くので、本質的かつ学力が高まります。
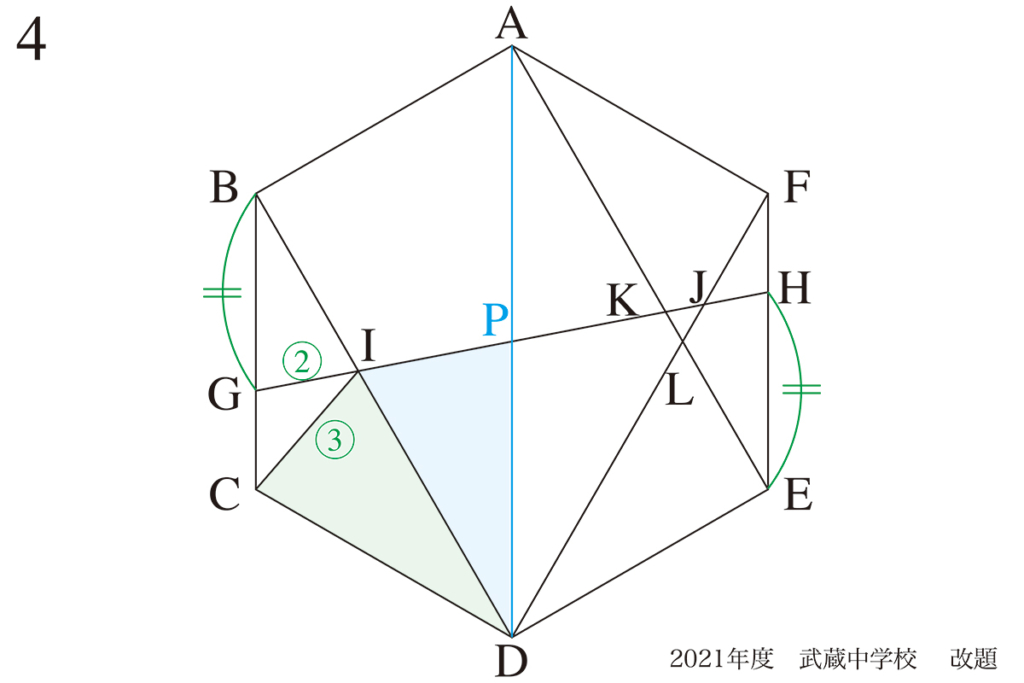
算数実践・問題4(2)の解法Aとして、相似三角形からいくつかの辺の比を求めました。（上記リンク）
そして、三角形の面積を求めました。
ここで、辺の比は解答以外の辺を求めても、同様に解答に至ります。
男子小学生確かに考え方が違っても、
求める面積や辺の比は「同じ」はずだね。
女子小学生解答と違う考え方って、
難しそうだけど・・・
いくつかの小問に別れている場合、そのうち一つでも「別の補助線」など考えると良いでしょう。
自分なりに相似三角形を見つけ、辺の比を求めてみましょう。
「解答以外の解き方にトライ」して答えが同じになれば、多くの場合「正しい考え方」です。
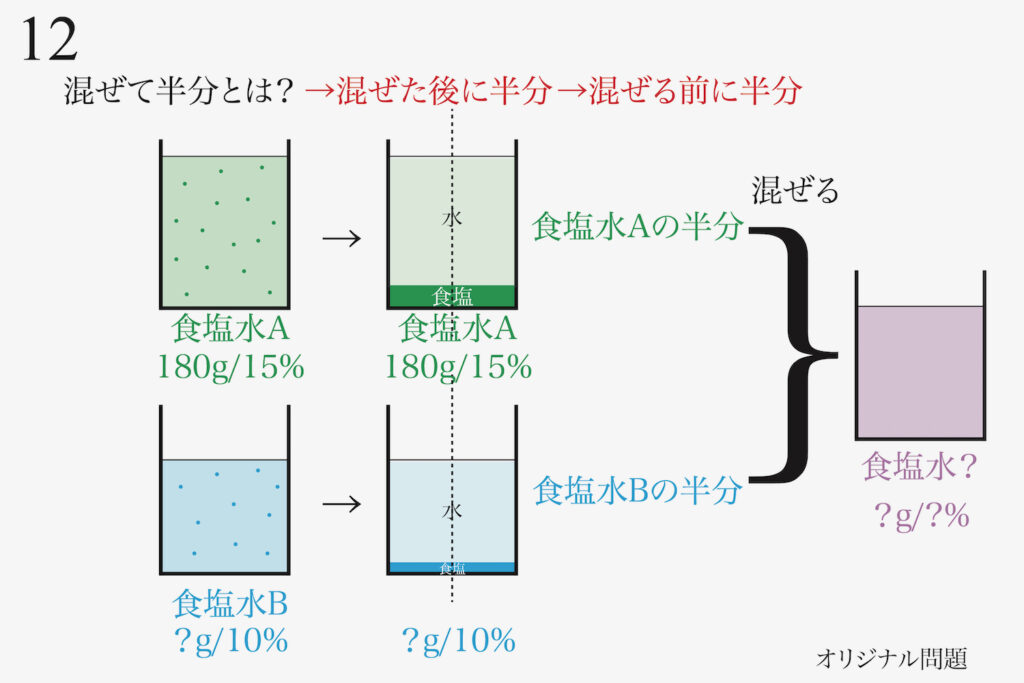
志望校の試験の難易度・学校の校風・カラーによって、学び方は異なります。
一方で、「基本的なスタンス」は共通しています。
漫然と解答を見るのではなく、頭と手を動かして「身体全体で学ぶ」姿勢でやってみましょう。
そして、一つ一つの解法を吸収して「自らのものにする」気持ちが大事です。
そのように、「対象とする問題を頭に入れる」感じで取り組んでみましょう。
先ほどの「問題を覚えてしまう」と同様に、「頭に入れる」は「暗記する」ではありません。
「暗記」ではなく、「考え方をしっかり理解し、頭に入れて、その引き出しをストックする」感じです。
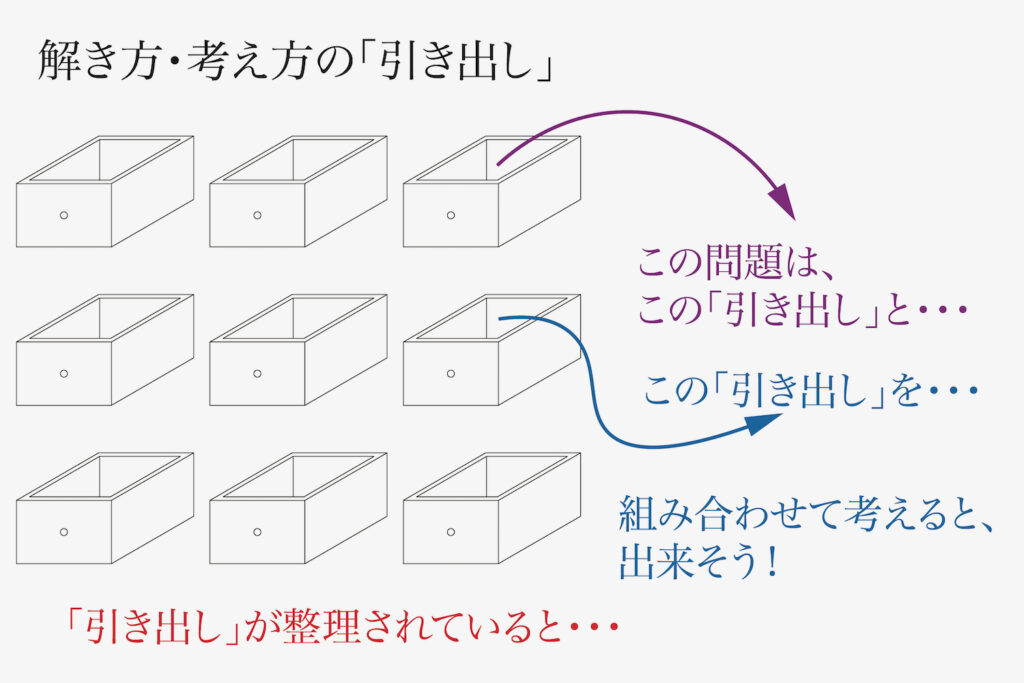
これからの模試で「解けなかった問題」に対しては、上記のような姿勢で試みると良いでしょう。
最難関校レベルの問題は、「解けば解くほど理解力が深まる」良問が多いです。
解く回数が増えるに従って味わいが変わって、学力が上がります。
問題への取り組み方によっては、「1題で10題〜20題分の効果がある」ようになります。
志望校の過去問は何度か取り組んでいて、「もう覚えてしまった」かもしれません。
「ちょっと異なる視点」を、「自分で」少し考えてみましょう。
学力は大きく、飛躍的に高まるでしょう。
次回は下記リンクです。
