前回は「図形問題の良い問題の考えるコツ〜三角形・相似比の考え方・平行な補助線・「苦手」に感じない姿勢・「思いつかない」から「思いつく」へ・色々な補助線を試行錯誤・問題2〜」の話でした。
問題2（再掲載）
下記の三角形ABCにおいて
BP : PC = 4 : 3
CQ : QA =3 : 5
AR : RB = 2 : 3
の時、下記を求めなさい。
(2) AS : SPの整数比
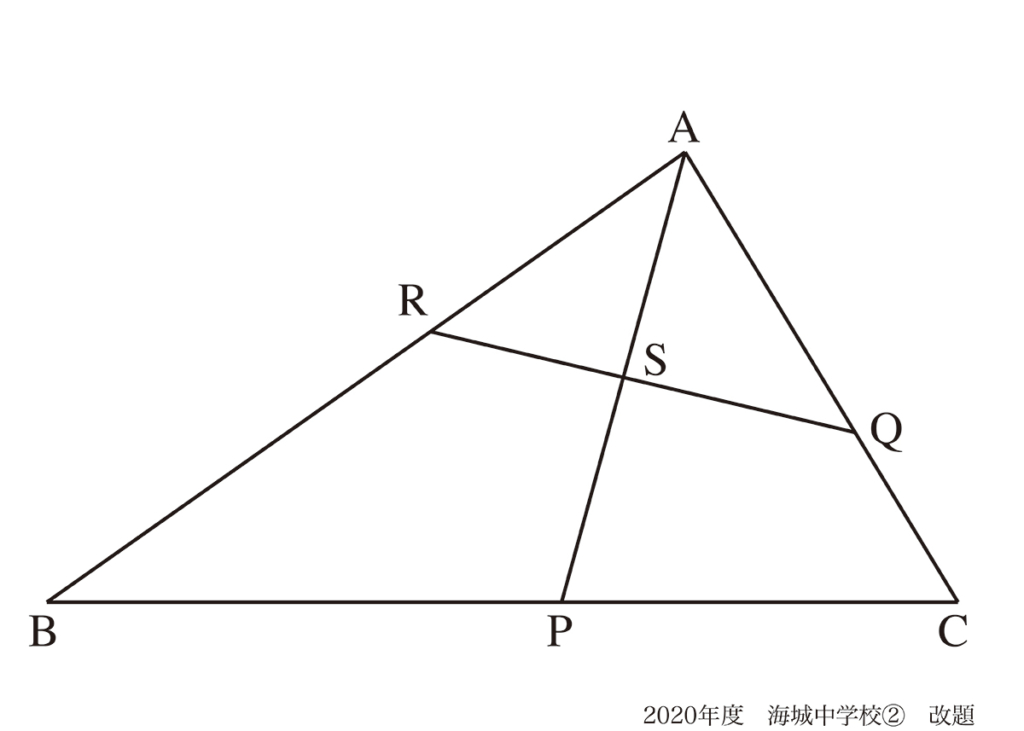
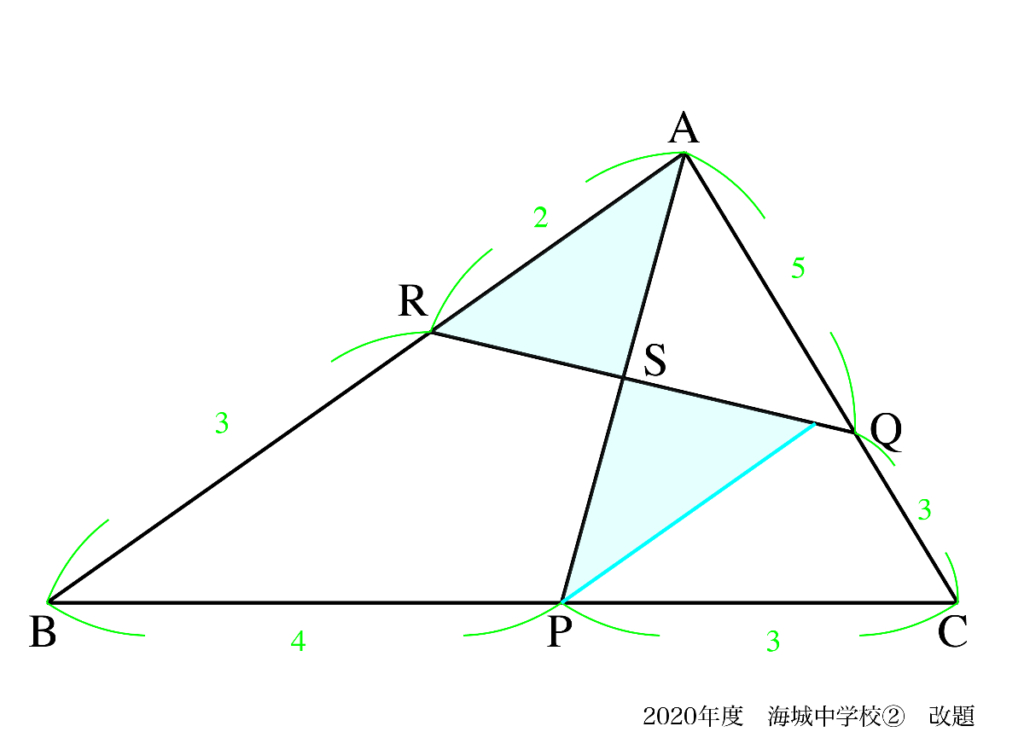
図形問題を「苦手」「嫌い」にならない姿勢：面積比(2)解法B
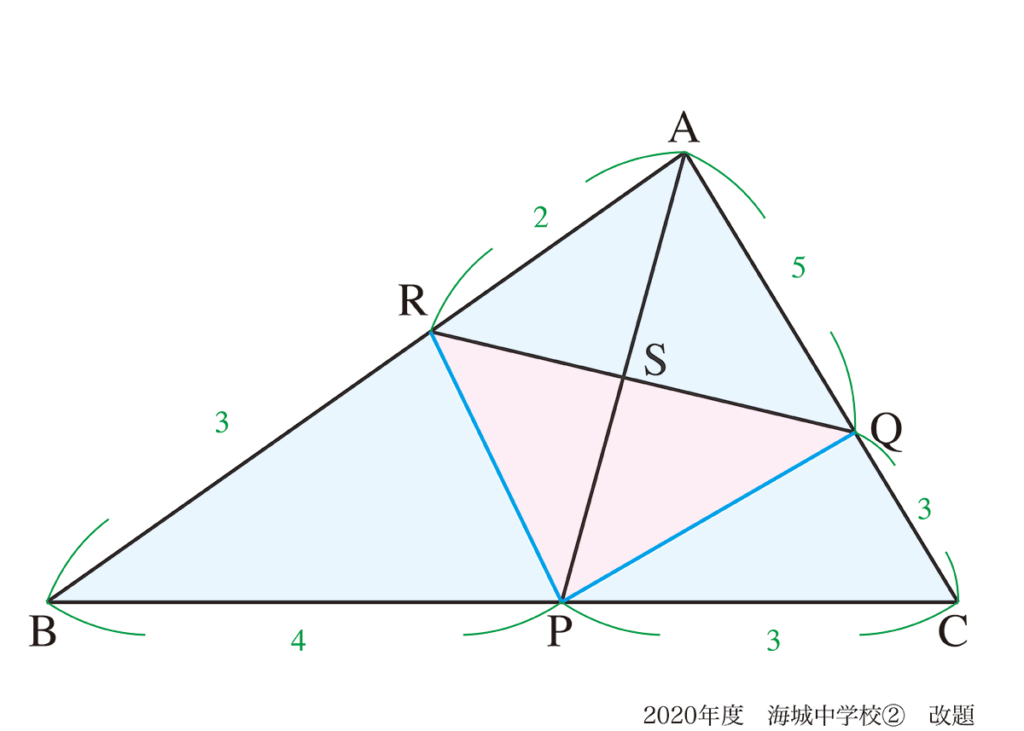
今回は(2)です。
この問題は非常にシンプルな構成で、三角形の図形問題の基本が学べます。
(1)では辺の比を利用した解き方・解法Aをおすすめしました。
(2) AS : SPは面積比を利用した解き方・解法Bの方が考えやすいので、こちらを先にご説明します。
(1)と同様に、「三角形の面積から辺の比」を考えましょう。
まず、考えやすい三角形になるように上手く分割しましょう。
上のように分けるのが良さそうです。
うん・・・
確かに良さそうだけど・・・
なかなかこういう補助線が
思いつかないから、「苦手」な気持ちになる・・・
苦手意識を持たずに「いろいろな補助線を引いてみる」と良いでしょう。
・「苦手」「嫌い」と思わないで、いろいろな補助線を引いてみる
・補助線を比較して、「良い補助線の理由」を考えてみる
AS : SP= △ARQ : △PRQで、△PRQは直接は求めにくいです。
代わりに、周囲の三角形の面積は比較的簡単に求まります。
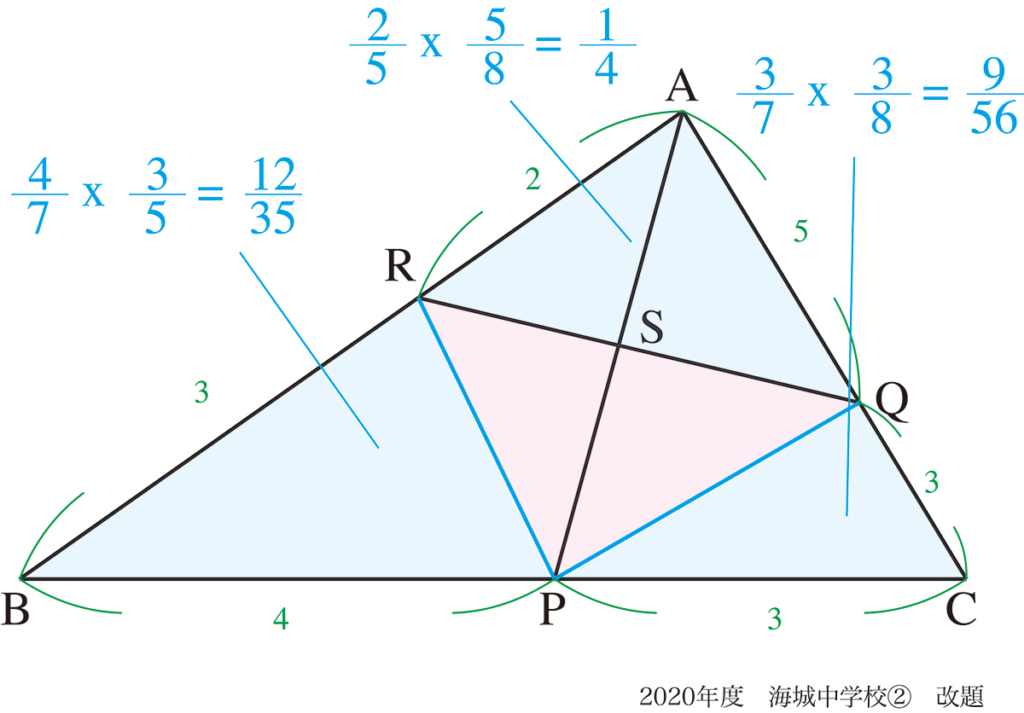
△ABCの面積を1とすると、上のようになります。
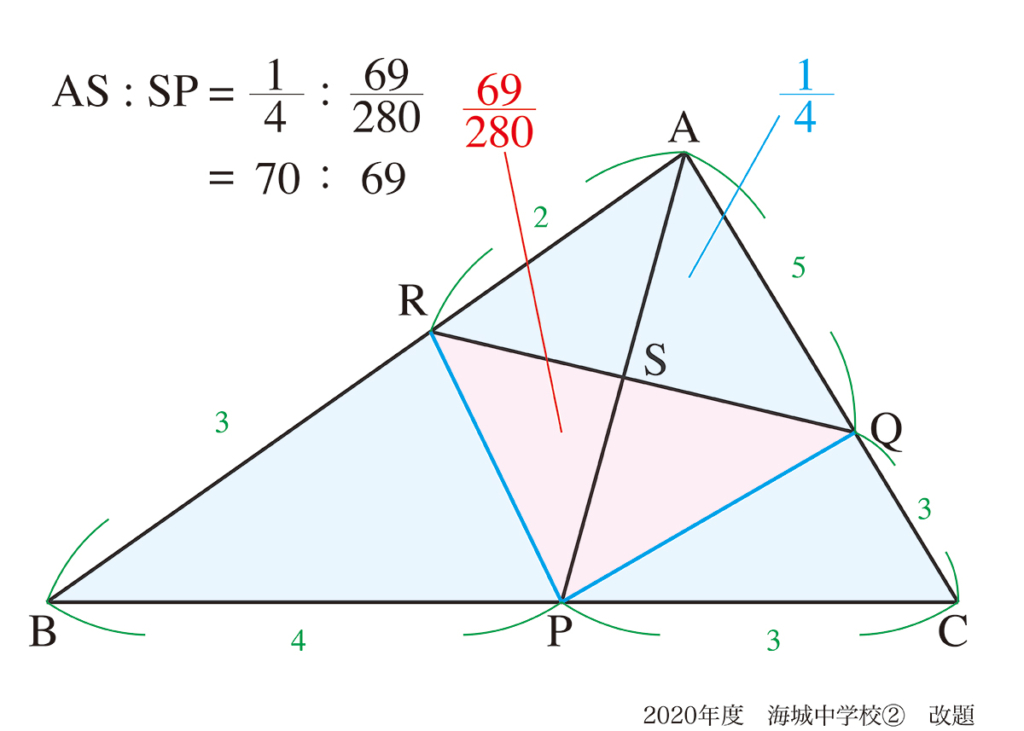
△PRQは△ABCから、周囲の3つの三角形の面積を引いて、上のようになります。
考え方は易しいのですが、計算は少し大変です。
計算力も大事ですから、こういう計算は
ふ〜ん・・・
と、解答を見て分かった気にならないことが、大事です。
・解答を読んで「分かった気持ち」にならない
・計算なども「目で追う」ではなく、「自分の手で書きながら、しっかり追う」
「単なる計算」であっても「見ただけ」にしないようにしましょう。
こういう計算も飛ばさずに、きちんと自分の手でやってみましょう。
すると、
ああ、
そいうことか・・・
と、気づくことがあります。
辺の比：(2)解法Aの考え方
解法Aと同様に、相似三角形から辺の比を考えましょう。
(1)の時とは異なり、「相似三角形」が見えてこないです。
近々ご紹介しますので、ぜひ考えてみてください。
