前回は「図形問題の解き方〜二つの長方形・面白い問題・補助線のコツ・自分で色々補助線を引いてみる・解答とは異なる補助線・「難しい」と感じない姿勢・補助線を比較して考える姿勢・見方を変える・問題1〜」の話でした。
今回も図形問題を考えてみましょう。
問題2・図形問題の良い問題
下記の三角形ABCにおいて
BP : PC = 4 : 3
CQ : QA =3 : 5
AR : RB = 2 : 3
の時、下記を求めなさい。
(1) RS : SQの整数比
(2) AS : SPの整数比
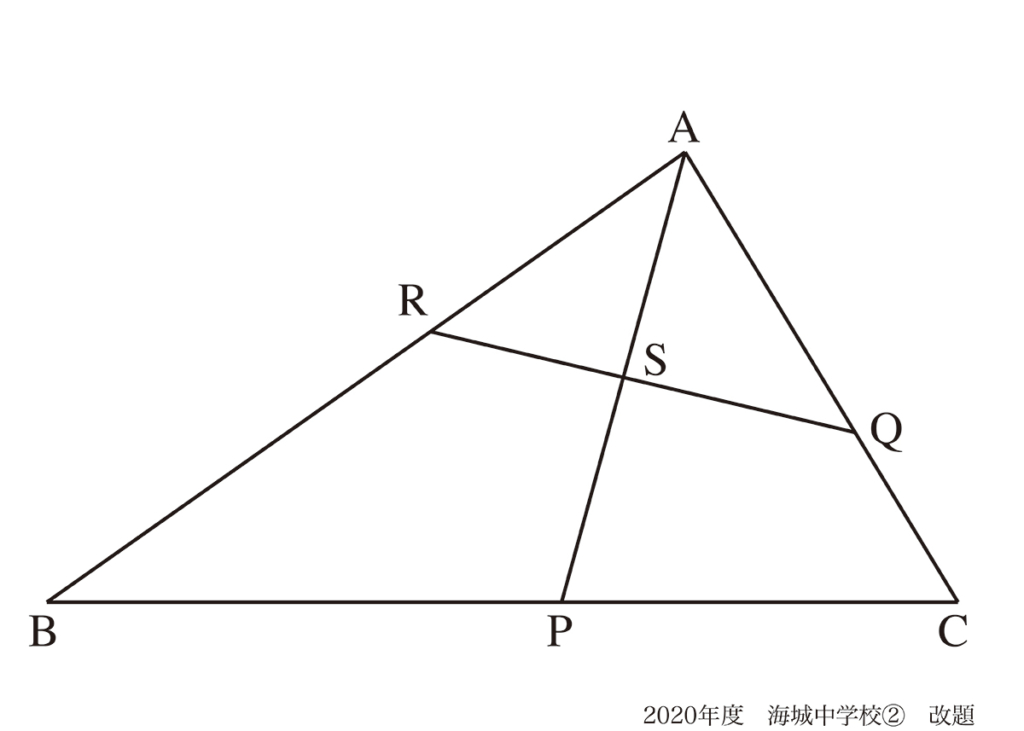
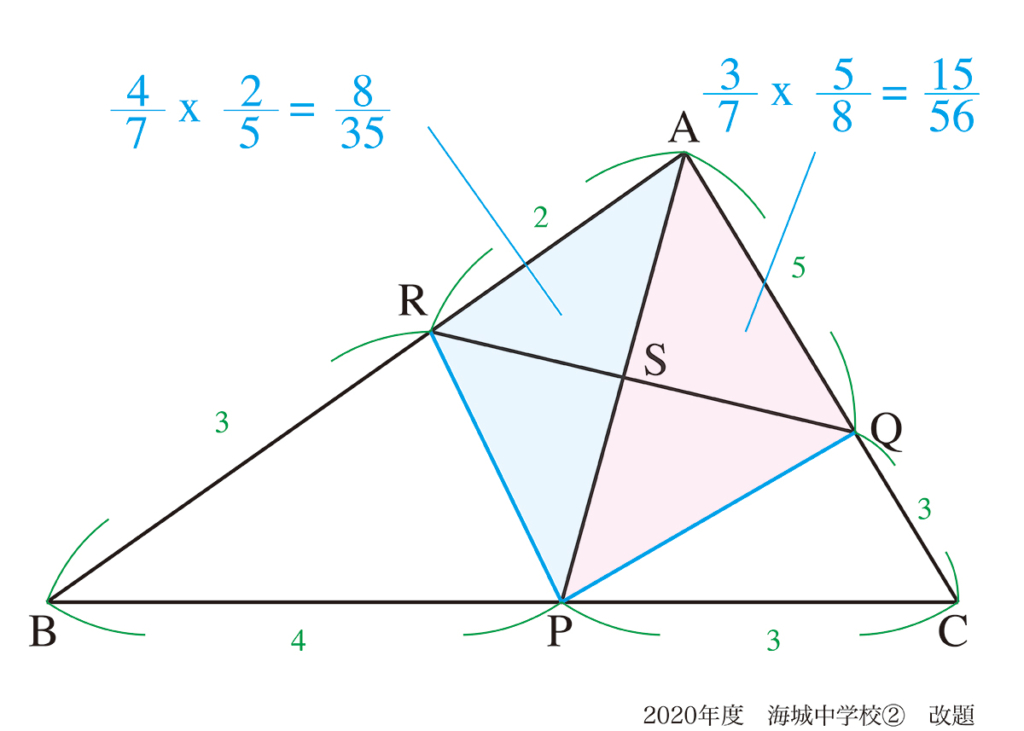
相似比の考え方・平行な補助線：解法A
三角形の問題は相似三角形ができるように補助線を引いて、辺の比を求めるのが基本的考え方です。
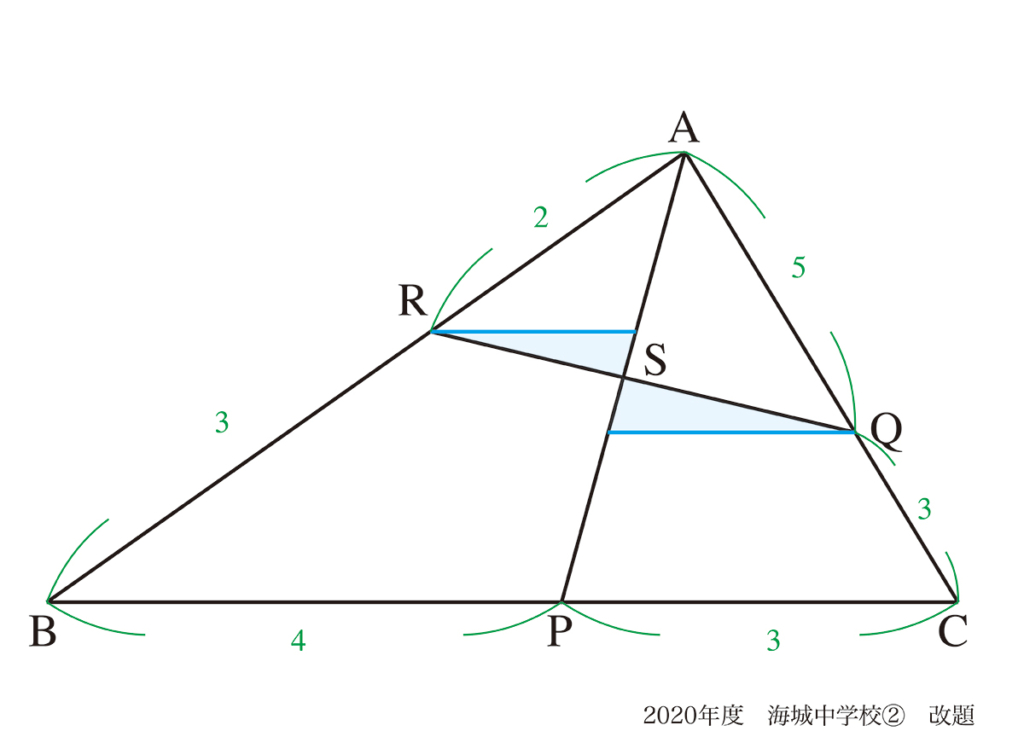
RとQを通りBCに平行な補助線を引けば、△ABP、△APCそれぞれの相似形が見えます。
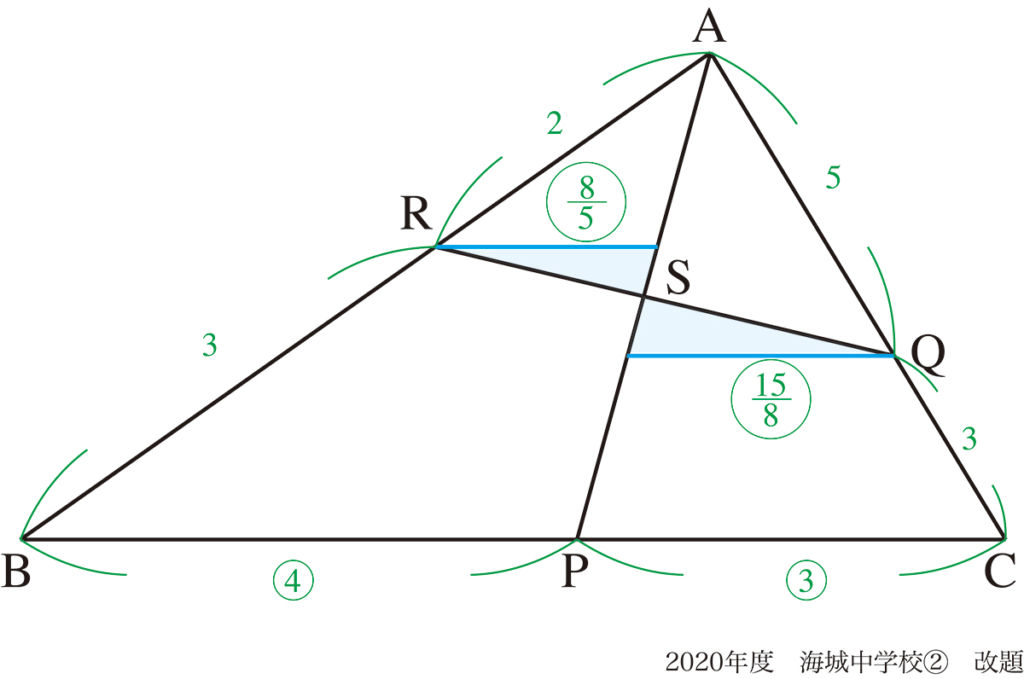
あとは相似比を考えて、それぞれの青線の長さが出ます。
そして、二つの青い三角形の相似比を考えれば、RS : SQは出ます。
答えは64 : 75です。
「苦手」に感じない姿勢：解法B
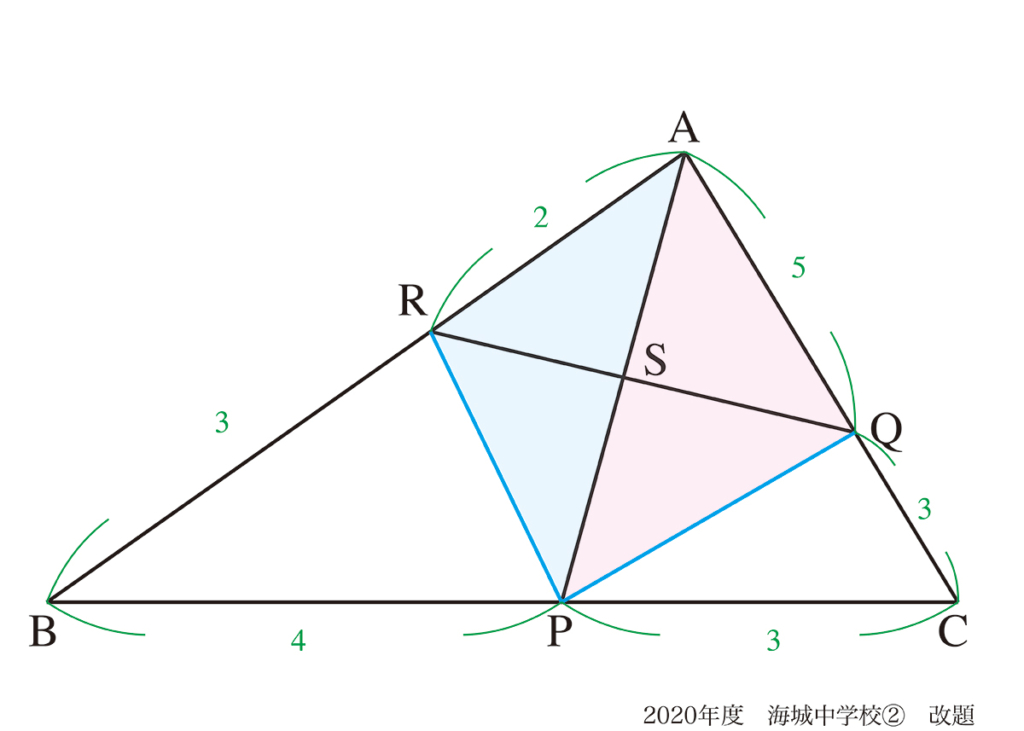
三角形の面積比に着目しましょう。
「辺を共有する三角形の面積比 = 高さに相当する辺の長さの比」です。
青と赤の三角形に着目すると、辺APを共有しています。
それぞれの三角形の面積比は、△ABCの面積を1とすると、上図のようになります。
ここで、△ARPと△AQPが「辺APを共有している」のがポイントです。
RS : SQ = △ARP : △AQPで求まります。
「思いつかない」から「思いつく」へ：色々な補助線を試行錯誤
解法Aも解法Bも、共に本質的な考え方です。
僕は相似形の基本を押さえている「解法A」を、おすすめします。
「解法B」も、面積と辺が関係する点では非常に有効です。
三角形の問題では、どれかの辺に平行な補助線をサッと引いて考えてみるのが良いでしょう。
まず、平行だったら
いいの？
「何かに平行な補助線」は、何らかの相似形が出てくる可能性が高いです。
そのように「自分で補助線を引いてみる」と、
補助線が
思いつかない・・・
と悩んでいる方も、少しずつ
あっ、この図形は
ひょっとしたらこの補助線がいいかも・・・
と補助線を「思いつく」ようになるでしょう。
(2)は似た問題ですが、いかがでしょうか。
解法Bと同様に考えると取り組みやすいですが、計算が少し大変です。
解法Aと同様には考えられますか。
補助線を引いても、なかなか相似三角形が見えてこないかもしれません。
この
補助線はどうだろう・・・
こう補助線を引くと、
どうなるかしら・・・
自分の手で色々と描いて、試行錯誤してみると「なにか見えてくること」があります。
少し考えてみてください。
