前回は「早起き算数・数学のメリット〜朝一番から頭が回転・早朝に算数を勉強・一日の間に頭の中で整理・受験生の一年間を健康に過ごして合格へ・朝から感じる充実感〜」の話でした。
問題 1:図形問題・二つの長方形・面白い問題

補助線のコツ:自分で色々補助線を引いてみる・解答A
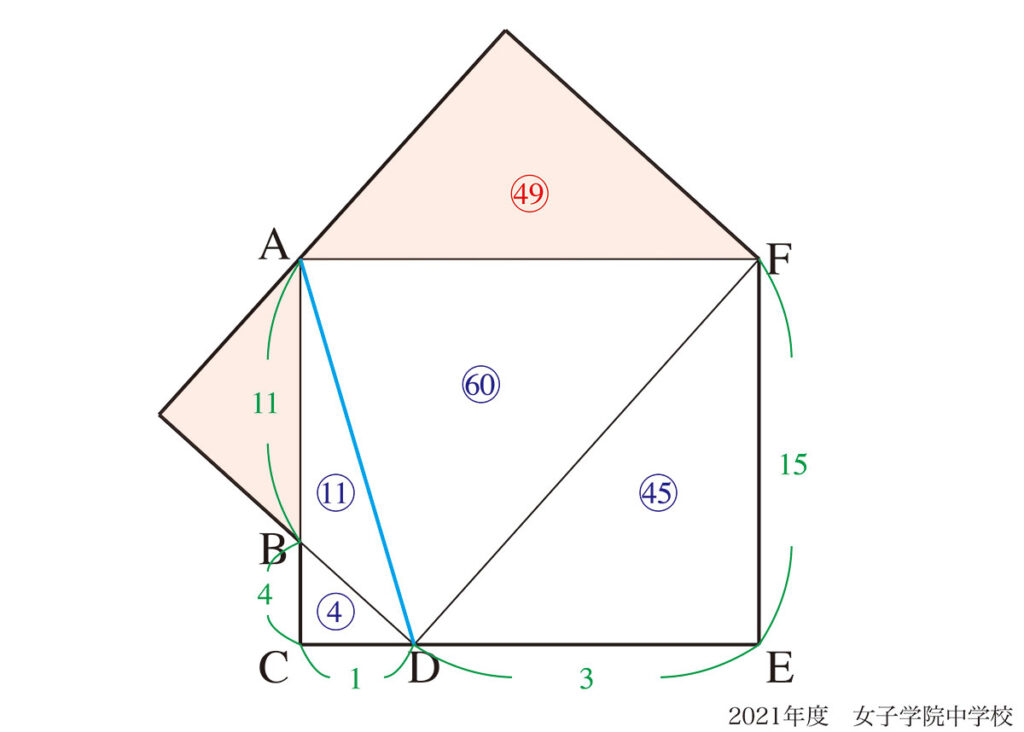
中学受験算数の実践的解法・考え方のご紹介です。
この問題は、いくつか補助線が考えられますが、最もシンプルな補助線はADです。
 男子小学生
男子小学生この補助線は
分かりやすいね!
ADに補助線を引いて、△ADFの面積が長方形の面積の半分であることがポイントです。
「三角形の辺の比=面積比」から△BCDの面積=④とおくと、次々と面積がもとまります。
この補助線のポイントは「△ADFの面積が二つの長方形の半分」であることです。
形がよく分からない二つの長方形ですが、「半分の面積なら分かる」のが大事なところです。
この解法を学んで、 上記のポイントに気づくように学ぶのが良いでしょう。
一方で図形問題は、様々な解法があります。
補助線の引き方で、「解ける・解けない」が決まることが多い図形問題。



この補助線に
気づかなかった・・・



僕って、
算数のセンスがないのかな・・・
補助線のコツ・ポイントはあります。
ところが、「それに気づくかどうか」と算数のセンスは大して関係ありません。



え、
そうなの?
補助線の引き方が上手くなる「最大のポイント・コツ」はあります。
その「ポイント・コツ」を身につける一番良い方法があります。



補助線のコツを
知りたい!
それは、自分で様々な補助線を試してみることです。



これは
役立つかな?



これは
イマイチかな?
色々考えながら補助線を引いているうちに、「良い補助線のコツ」が身に付いてゆきます。
解答とは異なる補助線:「難しい」と感じない姿勢・解答B
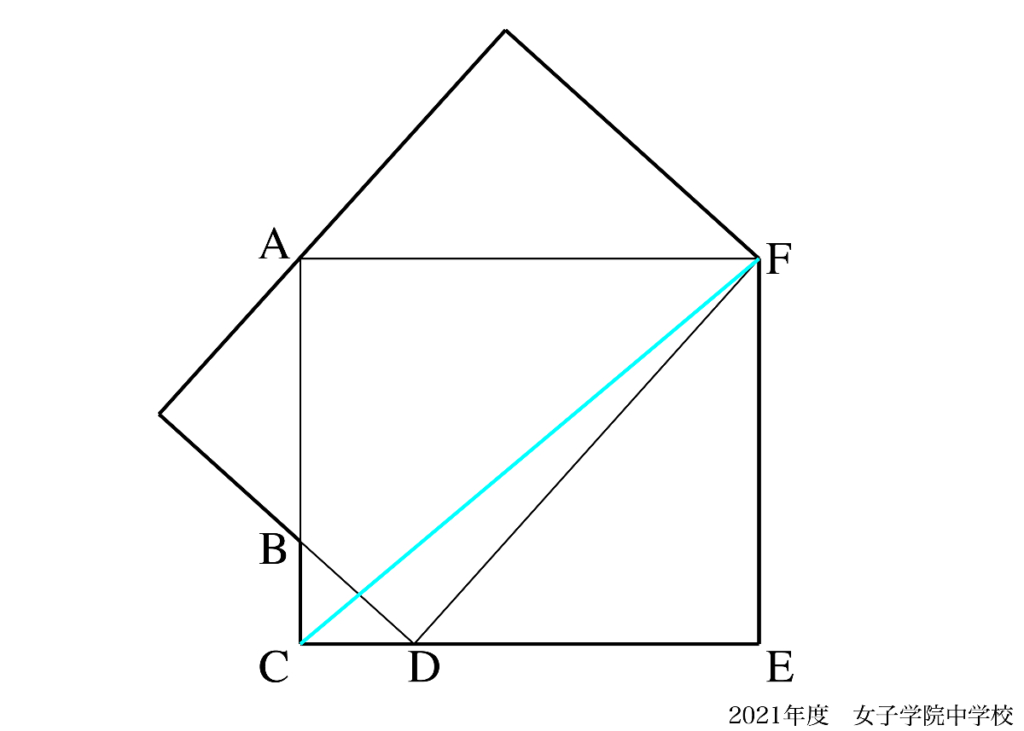

模範解答例に多い「最もシンプルな補助線」ではない補助線を考えて見ましょう。
上のように補助線を引いてみたら、解けないでしょうか。
少し考えてみましょう。
線が交差して、新しい交点が出きました。
補助線を引くときは「新しい交点は出ない方が良い」ことが多いです。
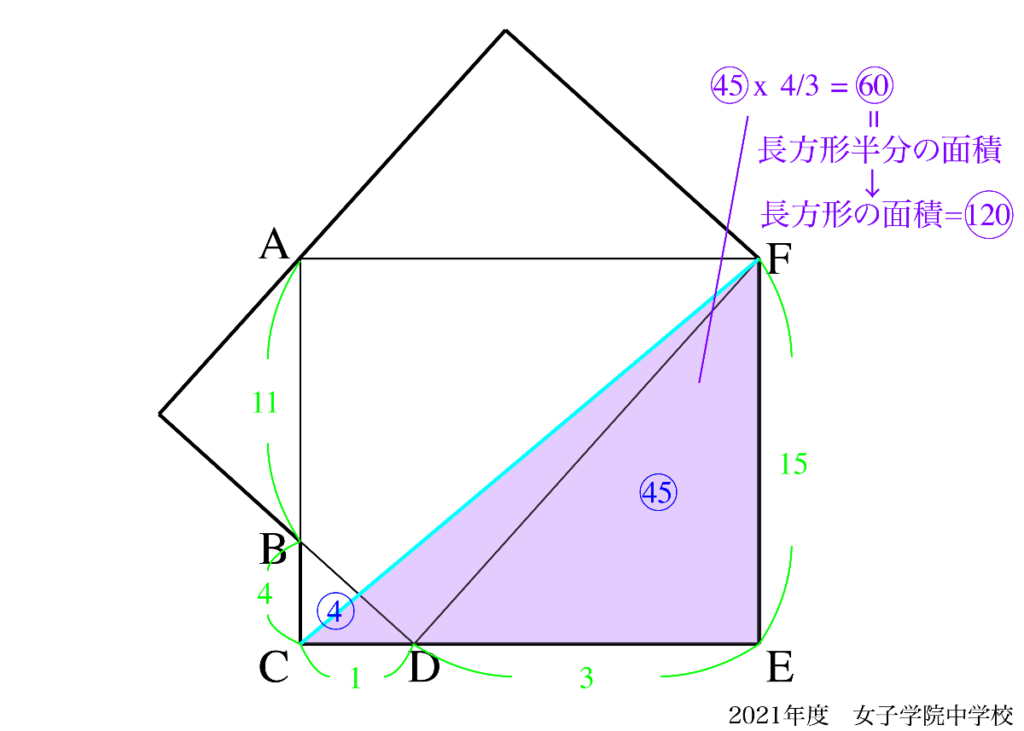

上のように考えてみましょう。
△CEFの面積は、長方形の面積の半分です。



これは
分かるよ!
△BCDと△DEGの辺の比から面積を考えると、長方形の半分の面積が分かります。
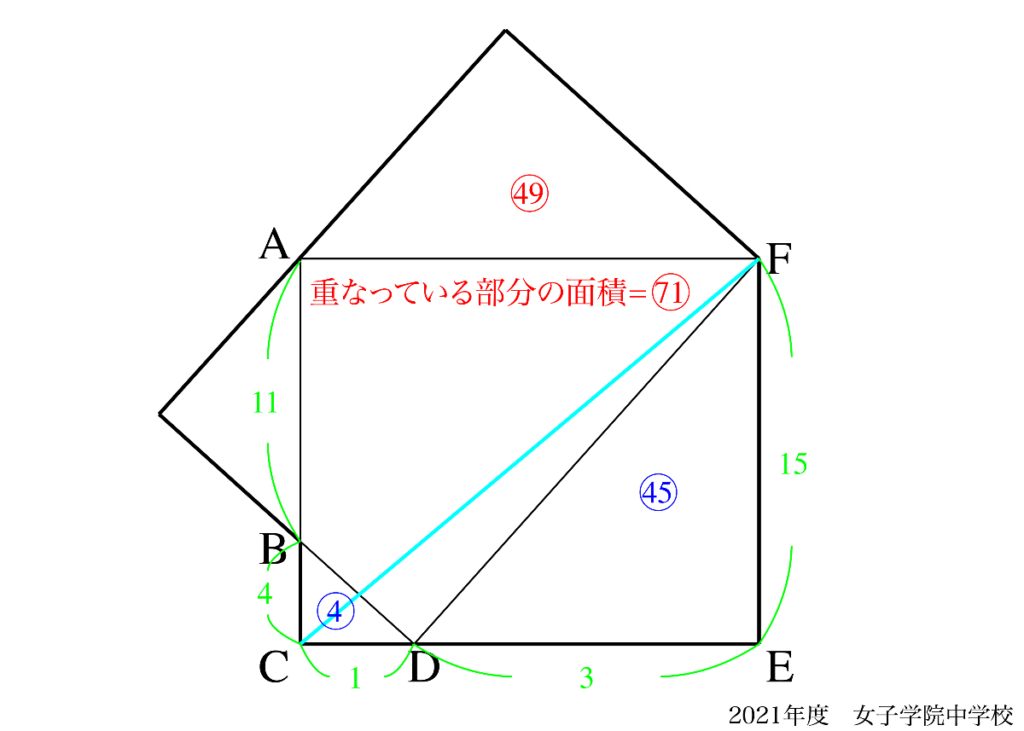

重なっている部分の面積は、長方形の面積から△BCDと△DEGの面積を引いて求められます。
120 – (45+4) = 71となります。
ここから、等積変形を考えてゆき、太枠内の図形の面積が求まります。
補助線を比較して考える姿勢:見方を変える
解答Bは、解答Aよりも少し遠回りです。
時間はかかりますが、悪い解法ではありません。
模範回答を学びつつ、少し遠回りな別解を学ぶことで、図形問題に対する様々な視点が学べます。
実際の試験では、図形問題で難航した時、



上手い補助線が、
思いつかない・・・
あるいは、



ひょっとしたら、
補助線が、間違っているのでは?
このように考えると、気持ちが焦ってしまうかもしれません。
「解にたどり着かない補助線」もありますが、見方を変えることで解く筋道が見えることも多いのです。
少し遠回りしても、解けることが大事です。
良問で「いくつかの解き方」を学ぶことは、大事です。
それは、「解答にたどりつく」腕力を鍛えるためにも大変効果的です。
次回は下記リンクです。


